2022-2023学年人教版八年级数学上册11.3 多边形及其内角和 精选题(含解析)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册11.3 多边形及其内角和 精选题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 193.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 10:27:29 | ||
图片预览

文档简介
11.3 多边形及其内角和精选题(含答案)-人教版八年级上册
一.选择题
1.如图,在五边形ABCDE中,AB∥ED,∠1,∠2,∠3分别是∠ABC,∠BCD,∠CDE的外角,则∠1+∠2+∠3的度数为( )
A.180° B.210° C.240° D.270°
2.如图,把△ABC纸片沿DE折叠,当点C落在四边形ABDE的外部时,此时测得∠1=106°,∠C=35°,则∠2的度数为( )
A.35° B.36° C.37° D.38°
3.下列长度的三条线段与长度为4的线段首尾依次相连能组成四边形的是( )
A.1,1,2 B.1,1,1 C.1,2,2 D.1,1,6
4.已知一个正多边形的一个内角是144°,则这个正多边形的边数是( )
A.8 B.9 C.10 D.11
.如图,图①是四边形纸条ABCD,其中AB∥CD,E,F分别为AB、CD上的两个点,将纸条ABCD沿EF折叠得到图②,再将图②沿DF折叠得到图③,若在图③中,∠FEM=24°,则∠EFC为( )
A.48° B.72° C.108° D.132°
.将一长方形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是( )
A.360° B.540° C.720° D.730°
.如图,CG平分正五边形ABCDE的外角∠DCF,并与∠EAB的平分线交于点O,则∠AOG的度数为( )
A.144° B.126° C.120° D.108°
.一个正多边形的一个内角是它相邻外角的5倍,则这个正多边形的边数是( )
A.12 B.10 C.8 D.6
.六角螺母的横截面是正六边形,这个正六边形的内角为( )
A.100° B.120° C.60° D.90°
.如图,七边形ABCDEFG中,EF,BA的延长线相交于点P,若∠ABC,∠BCD,∠CDE,∠DEF的外角的度数和为230°,则∠P的度数为( )
A.40° B.45° C.50° D.55°
二.填空题
.有一个正多边形的内角和等于它外角和的2倍,则这个正多边形每一个内角的大小为 .
.如图,五边形ABCDE中,AE∥BC,则∠C+∠D+∠E的度数为 .
.如图,四边形ABCD中,点M,N分别在AB,BC上,∠C=80°,按如图方式沿着MN折叠,使FN∥CD,此时量得∠FMN=40°,则∠B的度数是 .
.已知一个多边形的每个外角都是72度,那么它是 边形.
.如图,小亮从A点出发,沿直线前进10m向左转30°再沿直线前进10m,又向左转30°,照这样走下去,他第一次回到出发地A点时,一共走了 m.
解答题
.如图,∠1,∠2,∠3,∠4是四边形ABCD的四个外角.用两种方法证明∠1+∠2+∠3+∠4=360°.
.如图,在四边形ABCD中,∠B+∠ADC=180°,CE平分∠BCD交AB于点E,连接DE.
(1)若∠A=50°,∠B=85°,求∠BEC的度数;
(2)若∠A=∠1,求证:∠CDE=∠DCE.
.已知在四边形ABCD中,∠A=x,∠C=y,(0°<x<180°,0°<y<180°).
(1)∠ABC+∠ADC= (用含x、y的代数式表示);
(2)如图1,若x=y=90°,DE平分∠ADC,BF平分与∠ABC相邻的外角,请写出DE与BF的位置关系,并说明理由.
(3)如图2,∠DFB为四边形ABCD的∠ABC、∠ADC相邻的外角平分线所在直线构成的锐角,
①当x<y时,若x+y=140°,∠DFB=30°,试求x、y.
②小明在作图时,发现∠DFB不一定存在,请直接指出x、y满足什么条件时,∠DFB不存在.
.我们探究过三角形内角和等于180°,四边形内角和等于360°,请解决下面的问题:
(1)如图1,∠A+∠B+∠C+∠D=180°,则∠AOB+∠COD= (直接写出结果);
(2)连接AD、BC,若AO、BO、CO、DO分别是四边形ABCD的四个内角的平分线;
①如图2,如果∠AOB=110°,那么∠COD的度数为 (直接写出结果);
②如图3,若∠AOD=∠BOC,AB与CD平行吗?请写出理由.
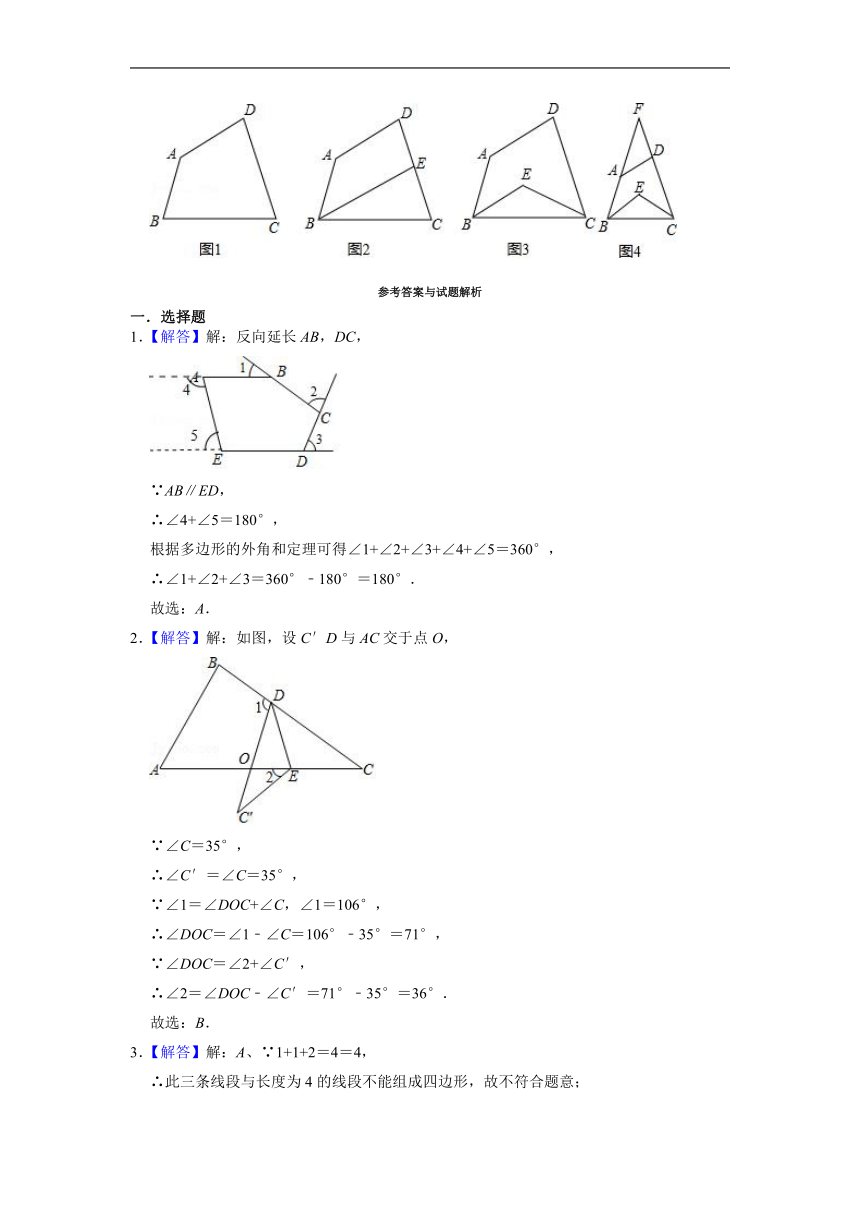
.如图,在四边形ABCD中,∠A=140°,∠D=80°.
(1)如图1,若∠B=∠C,则∠C= 度;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)①如图3,若∠ABC和∠DCB的角平分线交于点E,试求出∠BEC的度数;
②在①的条件下,若延长BA、CD交于点F(如图4).将原来条件“∠A=140°,∠D=80°”改为“∠F=40°”.其他条件不变.则∠BEC的度数为 .
参考答案与试题解析
一.选择题
1.【解答】解:反向延长AB,DC,
∵AB∥ED,
∴∠4+∠5=180°,
根据多边形的外角和定理可得∠1+∠2+∠3+∠4+∠5=360°,
∴∠1+∠2+∠3=360°﹣180°=180°.
故选:A.
2.【解答】解:如图,设C′D与AC交于点O,
∵∠C=35°,
∴∠C′=∠C=35°,
∵∠1=∠DOC+∠C,∠1=106°,
∴∠DOC=∠1﹣∠C=106°﹣35°=71°,
∵∠DOC=∠2+∠C′,
∴∠2=∠DOC﹣∠C′=71°﹣35°=36°.
故选:B.
3.【解答】解:A、∵1+1+2=4=4,
∴此三条线段与长度为4的线段不能组成四边形,故不符合题意;
B、∵1+1+1=3<4,
∴此三条线段与长度为5的线段能组成四边形,故不符合题意;
C、∵1+2+2=5>4,
∴此三条线段与长度为4的线段不能组成四边形,故符合题意;
D、∵1+1+4=6,
∴此三条线段与长度为4的线段不能组成四边形,故不符合题意;
故选:C.
4.【解答】解:设正多边形是n边形,由内角和公式得
(n﹣2)180°=144°×n,
解得n=10,
故选:C.
.【解答】解:如图②,由折叠得:∠B'EF=∠FEM=24°,
∵AE∥DF,
∴∠EFM=24°,∠BMF=∠DME=48°,
∵BM∥CF,
∴∠CFM+∠BMF=180°,
∴∠CFM=180°﹣48°=132°,
由折叠得:如图③,∠MFC=132°,
∴∠EFC=∠MFC﹣∠EFM=132°﹣24°=108°,
故选:C.
.【解答】解:设将一长方形纸片沿一条直线剪成两个多边形的边数分别为x、y.
∴这两个多边形的内角和之和为180°(x﹣2)+180°(y﹣2)=180°(x+y﹣4).
∴180°整除这两个多边形的内角和之和.
∵360°=180°×2,540°=180×3,720°=180°×4,180°不整除730°,
∴这两个多边形的内角和之和不可能是730°.
故选:D.
.【解答】解:∵任意多边形的外角和等于360°,
∴∠DCF=360°÷5=72°.
∴这个正五边形的每个内角为180°﹣72°=108°.
∴∠B=∠EAB=∠BCD=108°.
又∵AO平分∠EAB,
∴∠OAB=.
又∵CG平分∠DCF,
∴∠DCG=.
∴∠BCO=∠BCD+∠DCG=108°+36°=144°.
∴∠AOC=360°﹣(∠BAO+∠B+∠BCG)=360°﹣(54°+108°+144°)=54°.
∴∠AOG=180°﹣∠AOC=180°﹣54°=126°.
故选:B.
.【解答】解:设这个正多边的外角为x°,由题意得:
x+5x=180,
解得:x=30,
360°÷30°=12.
故选:A.
.【解答】解:∵这个正六边形的外角和等于360°,
∴每个外角=360°÷6=60°.
∴故这个正六边形的每一个内角的度数为=180°﹣60°=120°.
故选:B.
.【解答】解:如图.
由题意得:∠1+∠2+∠3+∠4=230°.
∴∠5+∠6+∠7=360°﹣230°=130°.
∵∠8=∠6+∠7,
∴∠5+∠8=130°.
∴∠P=180°﹣(∠5+∠8)=180°﹣130°=50°.
故选:C.
二.填空题
.【解答】解:∵一个正多边形的内角和等于它外角和的2倍,任意多边形的外角和都是360°,
∴这个多边形的内角和是360°×2=720°,
设这个正多边形的边数为n,
则(n﹣2)×180°=720°,
解得n=6,
故这个正多边形每一个内角的大小为720°÷6=120°,
故答案为:120°.
.【解答】解:过点D作DF∥AE,交AB于点F,
∵AE∥BC,
∴AE∥DF∥BC,
∴∠A+∠B=180°,∠E+∠EDF=180°,∠CDF+∠C=180°,
∴∠C+∠CDE+∠E=360°,
故答案为360°.
.【解答】解:∵FN∥DC,
∴∠BNF=∠C=80°,
∵△BMN沿MN翻折得△FMN,
∴∠BMN=∠FMN=40°,
∠BNM=∠BNF=×80°=40°,
在△BMN中,∠B=180°﹣(∠BMN+∠BNM)=180°﹣(40°+40°)=180°﹣80°=100°.
故答案为:100°.
.【解答】解:∵一个多边形的每个外角都是72度,
∴多边形的边数为=5,
故答案为:五.
.【解答】解:∵小亮每次都是沿直线前进10m后向左转30度,
∴他走过的图形是正多边形,
∴边数n=360°÷30°=12,
∴他第一次回到出发点A时,一共走了12×10=120m.
故答案为:120.
三.解答题
.【解答】证法1:
∵∠1+∠BAD=180°,∠2+∠ABC=180°,∠3+∠BCD=180°,∠4+∠CDA=180°,
∴∠1+∠BAD+∠2+∠ABC+∠3+∠BCD+∠4+∠CDA=180°×4=720°.
∵∠BAD+∠ABC+∠BCD+∠CDA=360°,
∴∠1+∠2+∠3+∠4=360°.
证法2:连接BD,
∵∠1=∠ABD+∠ADB,∠3=∠CBD+∠CDB,
∴∠1+∠2+∠3+∠4=∠ABD+∠ADB+∠2+∠CBD+∠CDB+∠4=180°×2=360°.
.【解答】(1)解:∵∠B+∠ADC=180°,∠A+∠B+∠BCD+∠ADC=360°,
∴∠A+∠BCD=180°,
∵∠A=50°,
∴∠BCD=130°,
∵CE平分∠BCD,
∴∠BCE=∠BCD=65°,
∵∠B=85°,
∴∠BEC=180°﹣∠BCE﹣∠B=180°﹣65°﹣85°=30°;
(2)证明:∵由(1)知:∠A+∠BCD=180°,
∴∠A+∠BCE+∠DCE=180°,
∵∠CDE+∠DCE+∠1=180°,∠1=∠A,
∴∠BCE=∠CDE,
∵CE平分∠BCD,
∴∠DCE=∠BCE,
∴∠CDE=∠DCE.
.【解答】解:(1)∠ABC+∠ADC=360°﹣x﹣y;
故答案为:360°﹣x﹣y;
(2)如图1,延长DE交BF于G
∵DE平分∠ADC,BF平分∠MBC,
∴∠CDE=∠ADC,∠CBF=∠CBM,
又∵∠CBM=180°﹣∠ABC=180°﹣(180°﹣∠ADC)=∠ADC,
∴∠CDE=∠CBF,
又∵∠BED=∠CDE+∠C=∠CBF+∠BGE,
∴∠BGE=∠C=90°,
∴DG⊥BF(即DE⊥BF);
(3)①由(1)得:∠CDN+∠CBM=x+y,
∵BF、DF分别平分∠CBM、∠CDN,
∴∠CDF+∠CBF=(x+y),
如图2,连接DB,则∠CBD+∠CDB=180°﹣y,
得∠FBD+∠FDB=180°﹣y+(x+y)=180°﹣y+x,
∴∠DFB=y﹣x=30°,
解方程组:,
解得:;
②当x=y时,∠ABC、∠ADC相邻的外角平分线所在直线互相平行,此时∠DFB不存在.
.【解答】解:(1)∵∠AOB+∠COD+∠A+∠B+∠C+∠D=180°×2=360°,∠A+∠B+∠C+∠D=180°,
∴∠AOB+∠COD=360°﹣180°=180°.
故答案为:180°;
(2)①∵AO、BO、CO、DO分别是四边形ABCD的四个内角的平分线,
∴∠OAB=∠DAB,∠OBA=∠CBA,∠OCD=∠BCD,∠ODC=∠ADC,
∴∠OAB+∠OBA+∠OCD+∠ODC=×360°=180°,
在△OAB中,∠OAB+∠OBA=180°﹣∠AOB,
在△OCD中,∠OCD+∠ODC=180°﹣∠COD,
∴180°﹣∠AOB+180°﹣∠COD=180°,
∴∠AOB+∠COD=180°;
∵∠AOB=110°,
∴∠COD=180°﹣110°=70°.
故答案为:70°;
②AB∥CD,理由如下:
∵AO、BO、CO、DO分别是四边形ABCD的四个内角的平分线,
∴∠OAB=∠DAB,∠OBA=∠CBA,∠OCD=∠BCD,∠ODC=∠ADC,
∴∠OAB+∠OBA+∠OCD+∠ODC=×360°=180°,
在△OAB中,∠OAB+∠OBA=180°﹣∠AOB,
在△OCD中,∠OCD+∠ODC=180°﹣∠COD,
∴180°﹣∠AOB+180°﹣∠COD=180°,
∴∠AOB+∠COD=180°;
∴∠AOD+∠BOC=360°﹣(∠AOB+∠COD)=360°﹣180°=180°,
∵∠AOD=∠BOC,
∴∠AOD=∠BOC=90°.
在∠AOD中,∠DAO+∠ADO=180°﹣∠AOD=180°﹣90°=90°,
∵∠DAO=∠DAB,∠ADO=∠ADC,
∴∠DAB+∠ADC=90°,
∴∠DAB+∠ADC=180°,
∴AB∥CD.
.【解答】解:(1)∵四边形ABCD中,∠A=140°,∠D=80°,
∴∠B+∠C=360°﹣(140°+80°)=140°,
∵∠B=∠C,
∴∠C=70°.
(2)∵BE∥AD,
∴∠ABE+∠A=180°,
∴∠ABE=180°﹣∠A=180°﹣140°=40°,
∵∠ABC的角平分线BE交DC于点E,
∴∠ABC=80°,
∴∠C=360°﹣(140°+80°+80°)=60°.
(3)①∵四边形ABCD中,∠A=140°,∠D=80°,
∴∠B+∠C=360°﹣(140°+80°)=140°,
∵∠ABC和∠BCD的角平分线交于点E,
∴∠EBC+∠ECB=70°,
∴∠BEC=180°﹣70°=110°.
②∵∠F=40°,
∴∠FBC+∠BCF=180°﹣40°=140°,
∵∠ABC和∠BCD的角平分线交于点E,
∴∠EBC+∠ECB=70°,
∴∠BEC=180°﹣70°=110°.
一.选择题
1.如图,在五边形ABCDE中,AB∥ED,∠1,∠2,∠3分别是∠ABC,∠BCD,∠CDE的外角,则∠1+∠2+∠3的度数为( )
A.180° B.210° C.240° D.270°
2.如图,把△ABC纸片沿DE折叠,当点C落在四边形ABDE的外部时,此时测得∠1=106°,∠C=35°,则∠2的度数为( )
A.35° B.36° C.37° D.38°
3.下列长度的三条线段与长度为4的线段首尾依次相连能组成四边形的是( )
A.1,1,2 B.1,1,1 C.1,2,2 D.1,1,6
4.已知一个正多边形的一个内角是144°,则这个正多边形的边数是( )
A.8 B.9 C.10 D.11
.如图,图①是四边形纸条ABCD,其中AB∥CD,E,F分别为AB、CD上的两个点,将纸条ABCD沿EF折叠得到图②,再将图②沿DF折叠得到图③,若在图③中,∠FEM=24°,则∠EFC为( )
A.48° B.72° C.108° D.132°
.将一长方形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是( )
A.360° B.540° C.720° D.730°
.如图,CG平分正五边形ABCDE的外角∠DCF,并与∠EAB的平分线交于点O,则∠AOG的度数为( )
A.144° B.126° C.120° D.108°
.一个正多边形的一个内角是它相邻外角的5倍,则这个正多边形的边数是( )
A.12 B.10 C.8 D.6
.六角螺母的横截面是正六边形,这个正六边形的内角为( )
A.100° B.120° C.60° D.90°
.如图,七边形ABCDEFG中,EF,BA的延长线相交于点P,若∠ABC,∠BCD,∠CDE,∠DEF的外角的度数和为230°,则∠P的度数为( )
A.40° B.45° C.50° D.55°
二.填空题
.有一个正多边形的内角和等于它外角和的2倍,则这个正多边形每一个内角的大小为 .
.如图,五边形ABCDE中,AE∥BC,则∠C+∠D+∠E的度数为 .
.如图,四边形ABCD中,点M,N分别在AB,BC上,∠C=80°,按如图方式沿着MN折叠,使FN∥CD,此时量得∠FMN=40°,则∠B的度数是 .
.已知一个多边形的每个外角都是72度,那么它是 边形.
.如图,小亮从A点出发,沿直线前进10m向左转30°再沿直线前进10m,又向左转30°,照这样走下去,他第一次回到出发地A点时,一共走了 m.
解答题
.如图,∠1,∠2,∠3,∠4是四边形ABCD的四个外角.用两种方法证明∠1+∠2+∠3+∠4=360°.
.如图,在四边形ABCD中,∠B+∠ADC=180°,CE平分∠BCD交AB于点E,连接DE.
(1)若∠A=50°,∠B=85°,求∠BEC的度数;
(2)若∠A=∠1,求证:∠CDE=∠DCE.
.已知在四边形ABCD中,∠A=x,∠C=y,(0°<x<180°,0°<y<180°).
(1)∠ABC+∠ADC= (用含x、y的代数式表示);
(2)如图1,若x=y=90°,DE平分∠ADC,BF平分与∠ABC相邻的外角,请写出DE与BF的位置关系,并说明理由.
(3)如图2,∠DFB为四边形ABCD的∠ABC、∠ADC相邻的外角平分线所在直线构成的锐角,
①当x<y时,若x+y=140°,∠DFB=30°,试求x、y.
②小明在作图时,发现∠DFB不一定存在,请直接指出x、y满足什么条件时,∠DFB不存在.
.我们探究过三角形内角和等于180°,四边形内角和等于360°,请解决下面的问题:
(1)如图1,∠A+∠B+∠C+∠D=180°,则∠AOB+∠COD= (直接写出结果);
(2)连接AD、BC,若AO、BO、CO、DO分别是四边形ABCD的四个内角的平分线;
①如图2,如果∠AOB=110°,那么∠COD的度数为 (直接写出结果);
②如图3,若∠AOD=∠BOC,AB与CD平行吗?请写出理由.
.如图,在四边形ABCD中,∠A=140°,∠D=80°.
(1)如图1,若∠B=∠C,则∠C= 度;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)①如图3,若∠ABC和∠DCB的角平分线交于点E,试求出∠BEC的度数;
②在①的条件下,若延长BA、CD交于点F(如图4).将原来条件“∠A=140°,∠D=80°”改为“∠F=40°”.其他条件不变.则∠BEC的度数为 .
参考答案与试题解析
一.选择题
1.【解答】解:反向延长AB,DC,
∵AB∥ED,
∴∠4+∠5=180°,
根据多边形的外角和定理可得∠1+∠2+∠3+∠4+∠5=360°,
∴∠1+∠2+∠3=360°﹣180°=180°.
故选:A.
2.【解答】解:如图,设C′D与AC交于点O,
∵∠C=35°,
∴∠C′=∠C=35°,
∵∠1=∠DOC+∠C,∠1=106°,
∴∠DOC=∠1﹣∠C=106°﹣35°=71°,
∵∠DOC=∠2+∠C′,
∴∠2=∠DOC﹣∠C′=71°﹣35°=36°.
故选:B.
3.【解答】解:A、∵1+1+2=4=4,
∴此三条线段与长度为4的线段不能组成四边形,故不符合题意;
B、∵1+1+1=3<4,
∴此三条线段与长度为5的线段能组成四边形,故不符合题意;
C、∵1+2+2=5>4,
∴此三条线段与长度为4的线段不能组成四边形,故符合题意;
D、∵1+1+4=6,
∴此三条线段与长度为4的线段不能组成四边形,故不符合题意;
故选:C.
4.【解答】解:设正多边形是n边形,由内角和公式得
(n﹣2)180°=144°×n,
解得n=10,
故选:C.
.【解答】解:如图②,由折叠得:∠B'EF=∠FEM=24°,
∵AE∥DF,
∴∠EFM=24°,∠BMF=∠DME=48°,
∵BM∥CF,
∴∠CFM+∠BMF=180°,
∴∠CFM=180°﹣48°=132°,
由折叠得:如图③,∠MFC=132°,
∴∠EFC=∠MFC﹣∠EFM=132°﹣24°=108°,
故选:C.
.【解答】解:设将一长方形纸片沿一条直线剪成两个多边形的边数分别为x、y.
∴这两个多边形的内角和之和为180°(x﹣2)+180°(y﹣2)=180°(x+y﹣4).
∴180°整除这两个多边形的内角和之和.
∵360°=180°×2,540°=180×3,720°=180°×4,180°不整除730°,
∴这两个多边形的内角和之和不可能是730°.
故选:D.
.【解答】解:∵任意多边形的外角和等于360°,
∴∠DCF=360°÷5=72°.
∴这个正五边形的每个内角为180°﹣72°=108°.
∴∠B=∠EAB=∠BCD=108°.
又∵AO平分∠EAB,
∴∠OAB=.
又∵CG平分∠DCF,
∴∠DCG=.
∴∠BCO=∠BCD+∠DCG=108°+36°=144°.
∴∠AOC=360°﹣(∠BAO+∠B+∠BCG)=360°﹣(54°+108°+144°)=54°.
∴∠AOG=180°﹣∠AOC=180°﹣54°=126°.
故选:B.
.【解答】解:设这个正多边的外角为x°,由题意得:
x+5x=180,
解得:x=30,
360°÷30°=12.
故选:A.
.【解答】解:∵这个正六边形的外角和等于360°,
∴每个外角=360°÷6=60°.
∴故这个正六边形的每一个内角的度数为=180°﹣60°=120°.
故选:B.
.【解答】解:如图.
由题意得:∠1+∠2+∠3+∠4=230°.
∴∠5+∠6+∠7=360°﹣230°=130°.
∵∠8=∠6+∠7,
∴∠5+∠8=130°.
∴∠P=180°﹣(∠5+∠8)=180°﹣130°=50°.
故选:C.
二.填空题
.【解答】解:∵一个正多边形的内角和等于它外角和的2倍,任意多边形的外角和都是360°,
∴这个多边形的内角和是360°×2=720°,
设这个正多边形的边数为n,
则(n﹣2)×180°=720°,
解得n=6,
故这个正多边形每一个内角的大小为720°÷6=120°,
故答案为:120°.
.【解答】解:过点D作DF∥AE,交AB于点F,
∵AE∥BC,
∴AE∥DF∥BC,
∴∠A+∠B=180°,∠E+∠EDF=180°,∠CDF+∠C=180°,
∴∠C+∠CDE+∠E=360°,
故答案为360°.
.【解答】解:∵FN∥DC,
∴∠BNF=∠C=80°,
∵△BMN沿MN翻折得△FMN,
∴∠BMN=∠FMN=40°,
∠BNM=∠BNF=×80°=40°,
在△BMN中,∠B=180°﹣(∠BMN+∠BNM)=180°﹣(40°+40°)=180°﹣80°=100°.
故答案为:100°.
.【解答】解:∵一个多边形的每个外角都是72度,
∴多边形的边数为=5,
故答案为:五.
.【解答】解:∵小亮每次都是沿直线前进10m后向左转30度,
∴他走过的图形是正多边形,
∴边数n=360°÷30°=12,
∴他第一次回到出发点A时,一共走了12×10=120m.
故答案为:120.
三.解答题
.【解答】证法1:
∵∠1+∠BAD=180°,∠2+∠ABC=180°,∠3+∠BCD=180°,∠4+∠CDA=180°,
∴∠1+∠BAD+∠2+∠ABC+∠3+∠BCD+∠4+∠CDA=180°×4=720°.
∵∠BAD+∠ABC+∠BCD+∠CDA=360°,
∴∠1+∠2+∠3+∠4=360°.
证法2:连接BD,
∵∠1=∠ABD+∠ADB,∠3=∠CBD+∠CDB,
∴∠1+∠2+∠3+∠4=∠ABD+∠ADB+∠2+∠CBD+∠CDB+∠4=180°×2=360°.
.【解答】(1)解:∵∠B+∠ADC=180°,∠A+∠B+∠BCD+∠ADC=360°,
∴∠A+∠BCD=180°,
∵∠A=50°,
∴∠BCD=130°,
∵CE平分∠BCD,
∴∠BCE=∠BCD=65°,
∵∠B=85°,
∴∠BEC=180°﹣∠BCE﹣∠B=180°﹣65°﹣85°=30°;
(2)证明:∵由(1)知:∠A+∠BCD=180°,
∴∠A+∠BCE+∠DCE=180°,
∵∠CDE+∠DCE+∠1=180°,∠1=∠A,
∴∠BCE=∠CDE,
∵CE平分∠BCD,
∴∠DCE=∠BCE,
∴∠CDE=∠DCE.
.【解答】解:(1)∠ABC+∠ADC=360°﹣x﹣y;
故答案为:360°﹣x﹣y;
(2)如图1,延长DE交BF于G
∵DE平分∠ADC,BF平分∠MBC,
∴∠CDE=∠ADC,∠CBF=∠CBM,
又∵∠CBM=180°﹣∠ABC=180°﹣(180°﹣∠ADC)=∠ADC,
∴∠CDE=∠CBF,
又∵∠BED=∠CDE+∠C=∠CBF+∠BGE,
∴∠BGE=∠C=90°,
∴DG⊥BF(即DE⊥BF);
(3)①由(1)得:∠CDN+∠CBM=x+y,
∵BF、DF分别平分∠CBM、∠CDN,
∴∠CDF+∠CBF=(x+y),
如图2,连接DB,则∠CBD+∠CDB=180°﹣y,
得∠FBD+∠FDB=180°﹣y+(x+y)=180°﹣y+x,
∴∠DFB=y﹣x=30°,
解方程组:,
解得:;
②当x=y时,∠ABC、∠ADC相邻的外角平分线所在直线互相平行,此时∠DFB不存在.
.【解答】解:(1)∵∠AOB+∠COD+∠A+∠B+∠C+∠D=180°×2=360°,∠A+∠B+∠C+∠D=180°,
∴∠AOB+∠COD=360°﹣180°=180°.
故答案为:180°;
(2)①∵AO、BO、CO、DO分别是四边形ABCD的四个内角的平分线,
∴∠OAB=∠DAB,∠OBA=∠CBA,∠OCD=∠BCD,∠ODC=∠ADC,
∴∠OAB+∠OBA+∠OCD+∠ODC=×360°=180°,
在△OAB中,∠OAB+∠OBA=180°﹣∠AOB,
在△OCD中,∠OCD+∠ODC=180°﹣∠COD,
∴180°﹣∠AOB+180°﹣∠COD=180°,
∴∠AOB+∠COD=180°;
∵∠AOB=110°,
∴∠COD=180°﹣110°=70°.
故答案为:70°;
②AB∥CD,理由如下:
∵AO、BO、CO、DO分别是四边形ABCD的四个内角的平分线,
∴∠OAB=∠DAB,∠OBA=∠CBA,∠OCD=∠BCD,∠ODC=∠ADC,
∴∠OAB+∠OBA+∠OCD+∠ODC=×360°=180°,
在△OAB中,∠OAB+∠OBA=180°﹣∠AOB,
在△OCD中,∠OCD+∠ODC=180°﹣∠COD,
∴180°﹣∠AOB+180°﹣∠COD=180°,
∴∠AOB+∠COD=180°;
∴∠AOD+∠BOC=360°﹣(∠AOB+∠COD)=360°﹣180°=180°,
∵∠AOD=∠BOC,
∴∠AOD=∠BOC=90°.
在∠AOD中,∠DAO+∠ADO=180°﹣∠AOD=180°﹣90°=90°,
∵∠DAO=∠DAB,∠ADO=∠ADC,
∴∠DAB+∠ADC=90°,
∴∠DAB+∠ADC=180°,
∴AB∥CD.
.【解答】解:(1)∵四边形ABCD中,∠A=140°,∠D=80°,
∴∠B+∠C=360°﹣(140°+80°)=140°,
∵∠B=∠C,
∴∠C=70°.
(2)∵BE∥AD,
∴∠ABE+∠A=180°,
∴∠ABE=180°﹣∠A=180°﹣140°=40°,
∵∠ABC的角平分线BE交DC于点E,
∴∠ABC=80°,
∴∠C=360°﹣(140°+80°+80°)=60°.
(3)①∵四边形ABCD中,∠A=140°,∠D=80°,
∴∠B+∠C=360°﹣(140°+80°)=140°,
∵∠ABC和∠BCD的角平分线交于点E,
∴∠EBC+∠ECB=70°,
∴∠BEC=180°﹣70°=110°.
②∵∠F=40°,
∴∠FBC+∠BCF=180°﹣40°=140°,
∵∠ABC和∠BCD的角平分线交于点E,
∴∠EBC+∠ECB=70°,
∴∠BEC=180°﹣70°=110°.
