2022-2023学年人教版八年级数学上册12.1 全等三角形 精选题(含解析)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册12.1 全等三角形 精选题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 233.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 10:31:31 | ||
图片预览


文档简介
12.1 全等三角形精选题(含答案)-人教版八年级上册
一.选择题
1.如图,已知△ABC≌△DEF,B,E,C,F在同一条直线上.若BF=8cm,BE=2cm,则CE的长度( )cm.
A.5 B.4 C.3 D.2
2.如图,△ABE≌△ACD,下列等式不一定正确的是( )
A.AB=AC B.∠BAD=∠CAE C.BE=CD D.AD=DE
3.如图,若△ABC≌△ADE,则下列结论中不成立的是( )
A.∠BAD=∠CAE B.∠BAD=∠CDE C.DA平分∠BDE D.AC=DE
4.如图,△ABC≌△A'B'C',其中∠A=37°,∠C'=23°,则∠B=( )
A.60° B.100° C.120° D.135°
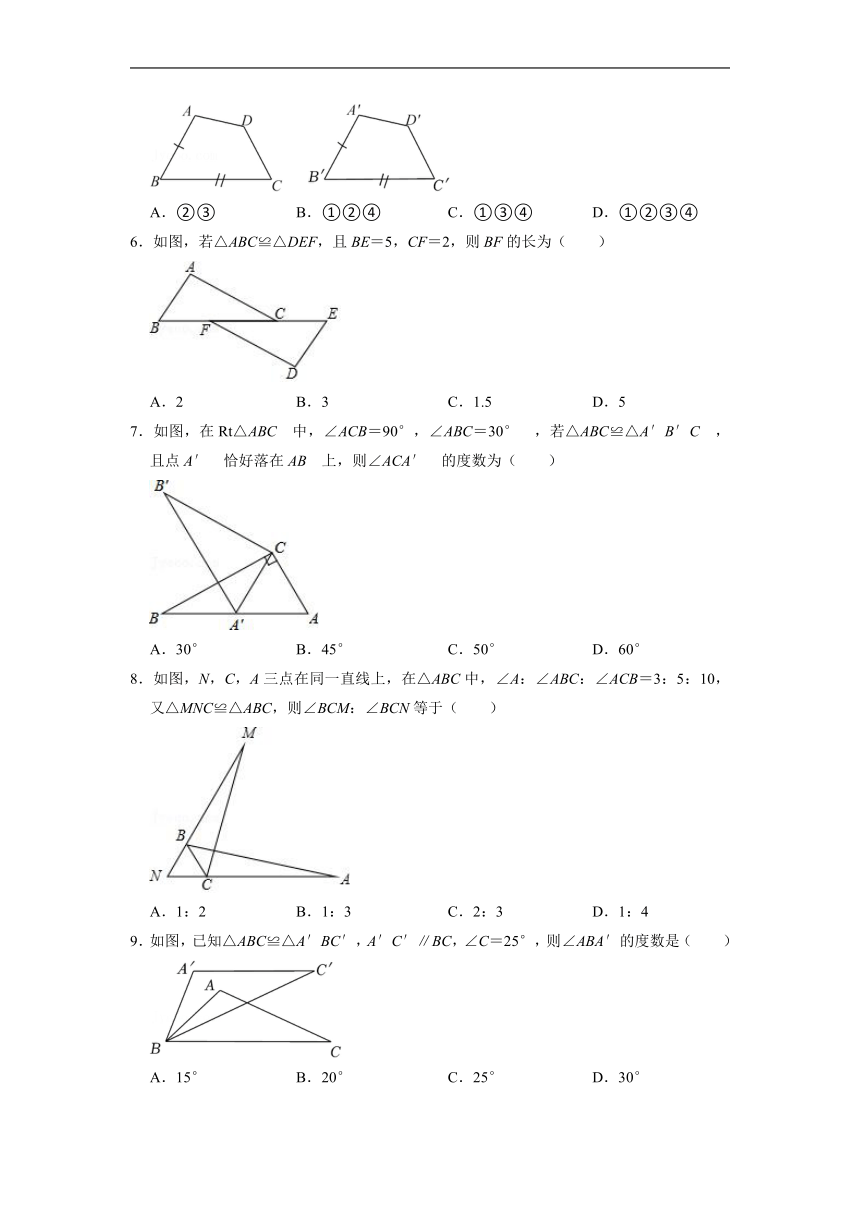
5.如图,在四边形ABCD与四边形A'B'C′D'中,AB=A'B',∠B=∠B',BC=B'C'.下列条件中:
①∠A=∠A′,AD=A′D′;
②∠A=∠A',∠D=∠D';
③∠A=∠A',CD=C'D';
④AD=A′D′,CD=C′D′.
添加上述条件中的其中一个,可使四边形ABCD≌四边形A′B′C′D′.上述条件中符合要求的有( )
A.②③ B.①②④ C.①③④ D.①②③④
6.如图,若△ABC≌△DEF,且BE=5,CF=2,则BF的长为( )
A.2 B.3 C.1.5 D.5
7.如图,在Rt△ABC 中,∠ACB=90°,∠ABC=30° ,若△ABC≌△A′B′C ,且点A′ 恰好落在AB 上,则∠ACA′ 的度数为( )
A.30° B.45° C.50° D.60°
8.如图,N,C,A三点在同一直线上,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,又△MNC≌△ABC,则∠BCM:∠BCN等于( )
A.1:2 B.1:3 C.2:3 D.1:4
9.如图,已知△ABC≌△A′BC′,A′C′∥BC,∠C=25°,则∠ABA′的度数是( )
A.15° B.20° C.25° D.30°
10.如图所示,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′,BE、CD交于点F,若∠BAC=45°,则∠BFC的大小是( )
A.90° B.100° C.105° D.110°
二.填空题
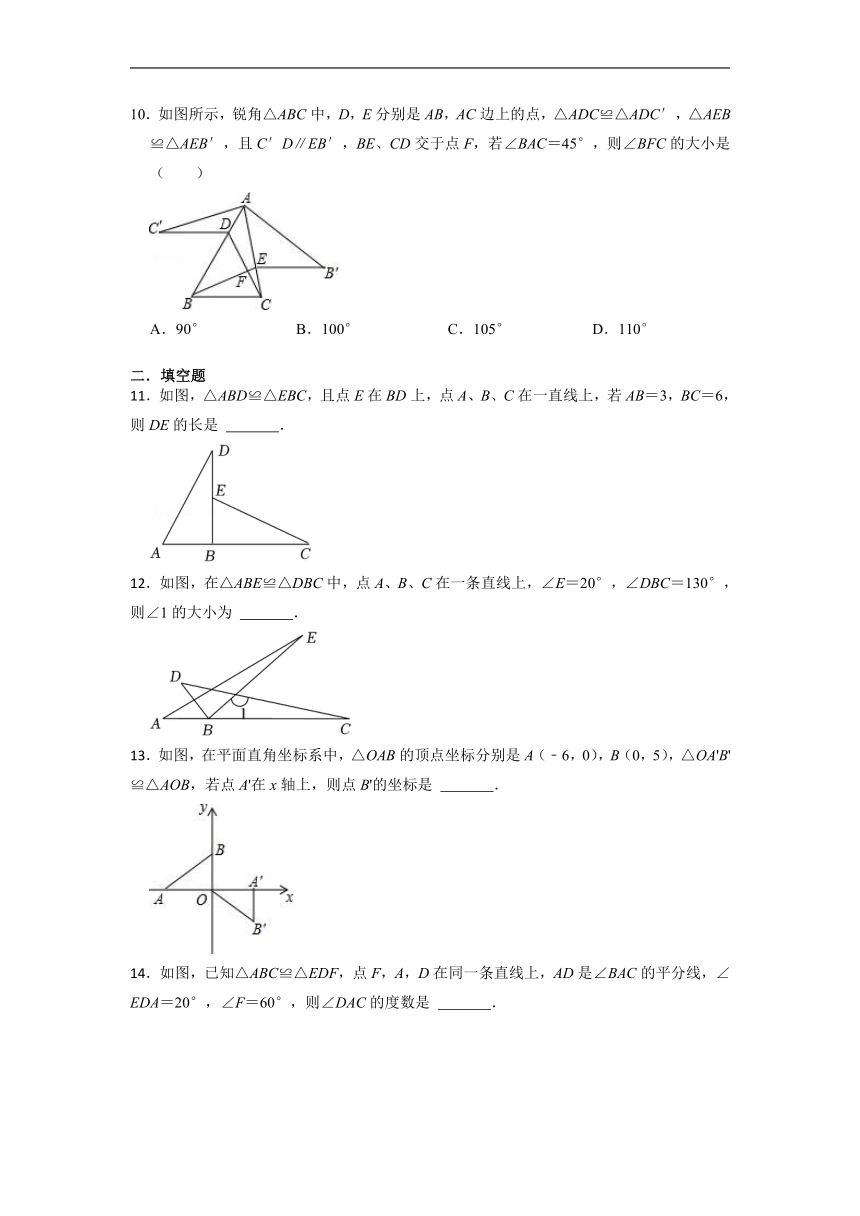
.如图,△ABD≌△EBC,且点E在BD上,点A、B、C在一直线上,若AB=3,BC=6,则DE的长是 .
.如图,在△ABE≌△DBC中,点A、B、C在一条直线上,∠E=20°,∠DBC=130°,则∠1的大小为 .
.如图,在平面直角坐标系中,△OAB的顶点坐标分别是A(﹣6,0),B(0,5),△OA'B'≌△AOB,若点A'在x轴上,则点B'的坐标是 .
.如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC的平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是 .
.如图,点D,E分别为△ABC的边AB,AC上,若△ADE≌△CFE.则下列结论①AD=CF;②AB∥CF;③AC⊥DF;④点E是AC的中点;不一定正确的是 (填写序号).
解答题
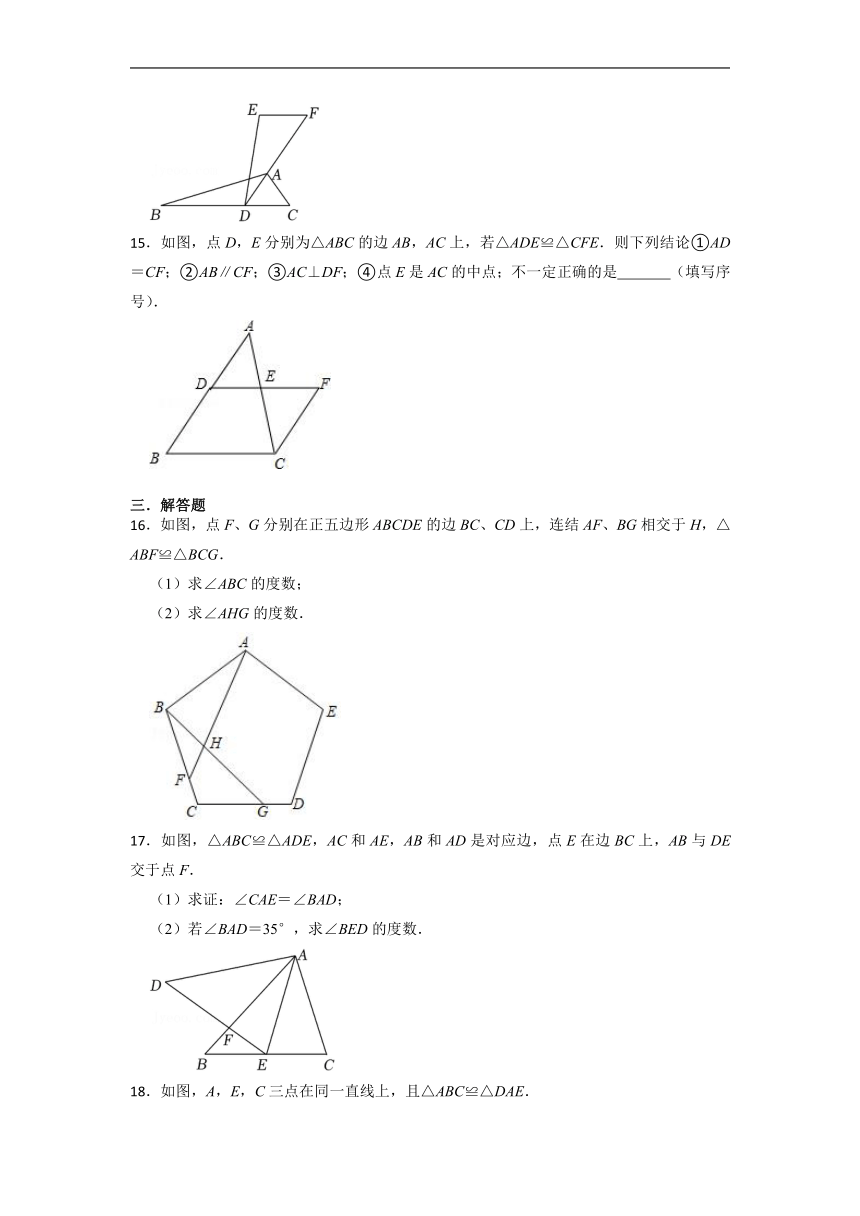
.如图,点F、G分别在正五边形ABCDE的边BC、CD上,连结AF、BG相交于H,△ABF≌△BCG.
(1)求∠ABC的度数;
(2)求∠AHG的度数.
.如图,△ABC≌△ADE,AC和AE,AB和AD是对应边,点E在边BC上,AB与DE交于点F.
(1)求证:∠CAE=∠BAD;
(2)若∠BAD=35°,求∠BED的度数.
.如图,A,E,C三点在同一直线上,且△ABC≌△DAE.
(1)线段DE,CE,BC有怎样的数量关系?请说明理由.
(2)请你猜想△ADE满足什么条件时,DE∥BC,并证明.
.如图所示,A,C,E三点在同一直线上,且△ABC≌△DAE.
(1)求证:BC=DE+CE;
(2)当△ABC满足什么条件时,BC∥DE?
.如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P,已知∠ABE=162°,∠DBC=30°,AD=DC=2.5,BC=4.
(1)求∠CBE的度数.
(2)求△CDP与△BEP的周长和.
参考答案与试题解析
一.选择题
1.【解答】解:∵△ABC≌△DEF,
∴BC=EF,
∴BC﹣CE=EF﹣CE,
∴BE=CF,
∵BE=2cm,
∴CF=BE=2cm,
∵BF=8cm,
∴CE=BF﹣BE﹣CF=8﹣2﹣2=4(cm),
故选:B.
2.【解答】解:∵△ABE≌△ACD,
∴AB=AC,BE=CD,AD=AE,∠BAE=∠CAD,
∴∠BAE﹣∠DAE=∠CAD﹣∠DAE,
∴∠BAD=∠CAE,
即只有选项D符合题意,选项A、选项B、选项C都不符合题意;
故选:D.
3.【解答】解:A.∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠BAD=∠CAE,故本选项不符合题意;
B.∵△ABC≌△ADE,
∴∠C=∠E,
∵∠AOE=∠DOC,∠E+∠CAE+∠AOE=180°,∠C+∠COD+∠,CDE=180°,
∴∠CAE=∠CDE,
∵∠BAD=∠CAE,
∴∠BAD=∠CDE,故本选项不符合题意;
C.∵△ABC≌△ADE,
∴∠B=∠ADE,AB=AD,
∴∠B=∠BDA,
∴∠BDA=∠ADE,
∴AD平分∠BDE,故本选项不符合题意;
D.∵△ABC≌△ADE,
∴BC=DE,故本选项符合题意;
故选:D.
4.【解答】解:∵△ABC≌△A'B'C',∠C'=23°,
∴∠C=∠C′=23°,
∵∠A=37°,
∴∠B=180°﹣∠A﹣∠C=180°﹣37°﹣23°=120°,
故选:C.
5.【解答】解:符合要求的条件是①②④,
证明:连接AC、A′C′,
在△ABC与△A′B′C′中,
,
∴△ABC≌△A′B′C′(SAS),
∴AC=A′C′,∠ACB=∠A′C′B′,∠ACB=∠A′C′B′,
∵∠BAD=∠B′A′D′,
∴∠BAD﹣∠DAC=∠B′A′D′﹣∠D′A′C′,
∴∠DAC=∠D′A′C′,
在△ACD和△A′C′D中,
,
∴△ACD≌△A′C′D′(SAS),
∴∠D=∠D′,∠ACD=∠A′C′D′,CD=C′D′,
∴∠BCD=∠B′C′D′,
∴四边形ABCD和四边形A′B′C′D′中,
AB=A′B′,BC=B′C′,AD=A′D′,DC=D′C′,
∠B=∠B′,∠BCD=∠B′C′D′,∠D=∠D′,∠BAD=∠B′A′D′,
∴四边形ABCD≌四边形A′B′C′D′.
同理根据②④的条件证得四边形ABCD≌四边形A′B′C′D′.
故选:B.
6.【解答】解:∵△ABC≌△DEF,
∴BC=EF,
∵BF=BC﹣FC,CE=FE﹣FC,
∴BF=CE,
∵BE=5,CF=2,
∴CF=BE﹣CE﹣BF,即2=5﹣2BF.
∴BF=1.5.
故选:C.
7.【解答】解:∵∠ACB=90°,∠ABC=3 0°,
∴∠A=90°﹣30°=60° ,
∵△ABC≌△A′B′C ,
∴CA′=CA,
∴△ACA′ 为等边三角形,
∴∠ACA′=60° ,
故选:D.
8.【解答】解:在△ABC中,∠A:∠ABC:∠ACB=3:5:10
设∠A=3x°,则∠ABC=5x°,∠ACB=10x°
3x+5x+10x=180
解得x=10
则∠A=30°,∠ABC=50°,∠ACB=100°
∴∠BCN=180°﹣100°=80°
又△MNC≌△ABC
∴∠ACB=∠MCN=100°
∴∠BCM=∠NCM﹣∠BCN=100°﹣80°=20°
∴∠BCM:∠BCN=20°:80°=1:4
故选:D.
9.【解答】解:∵△ABC≌△A′BC′,∠C=25°,
∴∠C=∠C′=25°,∠A′BC′=∠ABC,
∴∠A′BC′﹣∠ABC′=∠ABC﹣∠ABC′,
即∠ABA′=∠CBC′,
∵A′C′∥BC,∠C′=25°,
∴∠CBC′=∠C′=25°,
∴∠ABA′=25°,
故选:C.
10.【解答】解:延长C′D交AB′于H.
∵△AEB≌△AEB′,
∴∠ABE=∠AB′E,
∵C′H∥EB′,
∴∠AHC′=∠AB′E,
∴∠ABE=∠AHC′,
∵△ADC≌△ADC′,
∴∠C′=∠ACD,
∵∠BFC=∠DBF+∠BDF,∠BDF=∠CAD+∠ACD,
∴∠BFC=∠AHC′+∠C′+∠DAC,
∵∠DAC=∠DAC′=∠CAB′=45°,
∴∠C′AH=135°,
∴∠C′+∠AHC′=45°,
∴∠BFC=45°+45°=90°.
故选:A.
二.填空题
.【解答】解:∵△ABD≌△EBC,BC=6,AB=3,
∴BD=BC=6,BE=AB=3,
∴DE=BD﹣BE=6﹣3=3,
故答案为:3.
.【解答】解:∵△ABE≌△DBC,∠DBC=130°,
∴∠ABE=∠DBC=130°,
∴∠ABD+∠DBE+∠EBC+∠DBE=260°,
∵∠ABD+∠DBE+∠EBC=180°,
∴∠DBE=80°,
∴∠EBC=∠DBC﹣∠DBE=130°﹣80°=50°,
∴∠1=180°﹣∠C﹣∠EBC=180°﹣20°﹣50°=110°,
故答案为:110°.
.【解答】解:∵A(﹣6,0),B(0,5),
∴OA=6,OB=5,∠AOB=90°,
∵△OA'B'≌△AOB,
∴OA′=OA=6,A′B′=OB=5,∠B′A′O=90°,
∵点B′在第四象限,
∴点B′的坐标是(6,﹣5),
故答案为:(6,﹣5).
.【解答】解:∵△ABC≌△EDF,
∴∠B=∠EDF,∠C=∠F,
∵∠EDA=20°,∠F=60°,
∴∠B=20°,∠C=60°,
∴∠BAC=180°﹣∠B﹣∠C=100°,
∵AD是∠BAC的平分线,
∴∠DAC=BAC=50°,
故答案为:50°.
.【解答】解:∵△ADE≌△CFE,
∴AD=CF,∠A=∠ECF,AE=CE,
∴AB∥CF,点E是AC的中点
∴①②④正确;
∵∠AED不一定为直角
∴AC⊥DF不一定成立
∴③不正确.
故答案为③.
三.解答题
.【解答】解:(1)∵正五边形的内角和为:(5﹣2)×180°=540°,
∴∠ABC=×540°=108°;
(2)∵△ABF≌△BCG,
∴∠BAF=∠CBG,
∵∠BAF+∠ABH=∠AHG,
∴∠CBH+∠ABH=∠AHG=∠ABC=×540°=108°,
∴∠AHG=108°.
.【解答】(1)证明:∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC﹣∠BAE=∠DAE﹣∠BAE,
∴∠CAE=∠BAD;
(2)解:∵△ABC≌△ADE,
∴∠D=∠B,
∵∠AFD=∠EFB,∠D+∠BAD+∠AFD=180°,∠B+∠EFB+∠BED=180°,
∴∠BED=∠BAD,
∵∠BAD=35°,
∴∠BED=35°.
.【解答】(1)解:DE=CE+BC.
理由:∵△ABC≌△DAE,
∴AE=BC,DE=AC.
∵A,E,C三点在同一直线上,
∴AC=AE+CE,
∴DE=CE+BC;
(2)当△ADE满足∠AED=90°时,DE∥BC,
证明:∵△ABC≌△DAE,∠AED=90°,
∴∠C=∠AED=90°,∠DEC=180°﹣∠AED=90°,
∴∠C=∠DEC.
∴DE∥BC,
即当△ADE满足∠AED=90°时,DE∥BC.
.【解答】(1)证明:∵△ABC≌△DAE,
∴AE=BC,AC=DE,
又∵AE=AC+CE,
∴BC=DE+CE;
(2)解:∵BC∥DE,
∴∠BCE=∠E,
又∵△ABC≌△DAE,
∴∠ACB=∠E,
∴∠ACB=∠BCE,
又∵∠ACB+∠BCE=180°,
∴∠ACB=90°,
即当△ABC满足∠ACB为直角时,BC∥DE.
.【解答】解:(1)∵∠ABE=162°,∠DBC=30°,
∴∠ABD+∠CBE=132°,
∵△ABC≌△DBE,
∴∠ABC=∠DBE,
∴∠ABD=∠CBE=132°÷2=66°,
即∠CBE的度数为66°;
(2)∵△ABC≌△DBE,
∴DE=AC=AD+DC=5,BE=BC=4,
∴△CDP与△BEP的周长和=DC+DP+PC+BP+PE+BE=DC+DE+BC+BE=2.5+5+4+4=15.5.
一.选择题
1.如图,已知△ABC≌△DEF,B,E,C,F在同一条直线上.若BF=8cm,BE=2cm,则CE的长度( )cm.
A.5 B.4 C.3 D.2
2.如图,△ABE≌△ACD,下列等式不一定正确的是( )
A.AB=AC B.∠BAD=∠CAE C.BE=CD D.AD=DE
3.如图,若△ABC≌△ADE,则下列结论中不成立的是( )
A.∠BAD=∠CAE B.∠BAD=∠CDE C.DA平分∠BDE D.AC=DE
4.如图,△ABC≌△A'B'C',其中∠A=37°,∠C'=23°,则∠B=( )
A.60° B.100° C.120° D.135°
5.如图,在四边形ABCD与四边形A'B'C′D'中,AB=A'B',∠B=∠B',BC=B'C'.下列条件中:
①∠A=∠A′,AD=A′D′;
②∠A=∠A',∠D=∠D';
③∠A=∠A',CD=C'D';
④AD=A′D′,CD=C′D′.
添加上述条件中的其中一个,可使四边形ABCD≌四边形A′B′C′D′.上述条件中符合要求的有( )
A.②③ B.①②④ C.①③④ D.①②③④
6.如图,若△ABC≌△DEF,且BE=5,CF=2,则BF的长为( )
A.2 B.3 C.1.5 D.5
7.如图,在Rt△ABC 中,∠ACB=90°,∠ABC=30° ,若△ABC≌△A′B′C ,且点A′ 恰好落在AB 上,则∠ACA′ 的度数为( )
A.30° B.45° C.50° D.60°
8.如图,N,C,A三点在同一直线上,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,又△MNC≌△ABC,则∠BCM:∠BCN等于( )
A.1:2 B.1:3 C.2:3 D.1:4
9.如图,已知△ABC≌△A′BC′,A′C′∥BC,∠C=25°,则∠ABA′的度数是( )
A.15° B.20° C.25° D.30°
10.如图所示,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′,BE、CD交于点F,若∠BAC=45°,则∠BFC的大小是( )
A.90° B.100° C.105° D.110°
二.填空题
.如图,△ABD≌△EBC,且点E在BD上,点A、B、C在一直线上,若AB=3,BC=6,则DE的长是 .
.如图,在△ABE≌△DBC中,点A、B、C在一条直线上,∠E=20°,∠DBC=130°,则∠1的大小为 .
.如图,在平面直角坐标系中,△OAB的顶点坐标分别是A(﹣6,0),B(0,5),△OA'B'≌△AOB,若点A'在x轴上,则点B'的坐标是 .
.如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC的平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是 .
.如图,点D,E分别为△ABC的边AB,AC上,若△ADE≌△CFE.则下列结论①AD=CF;②AB∥CF;③AC⊥DF;④点E是AC的中点;不一定正确的是 (填写序号).
解答题
.如图,点F、G分别在正五边形ABCDE的边BC、CD上,连结AF、BG相交于H,△ABF≌△BCG.
(1)求∠ABC的度数;
(2)求∠AHG的度数.
.如图,△ABC≌△ADE,AC和AE,AB和AD是对应边,点E在边BC上,AB与DE交于点F.
(1)求证:∠CAE=∠BAD;
(2)若∠BAD=35°,求∠BED的度数.
.如图,A,E,C三点在同一直线上,且△ABC≌△DAE.
(1)线段DE,CE,BC有怎样的数量关系?请说明理由.
(2)请你猜想△ADE满足什么条件时,DE∥BC,并证明.
.如图所示,A,C,E三点在同一直线上,且△ABC≌△DAE.
(1)求证:BC=DE+CE;
(2)当△ABC满足什么条件时,BC∥DE?
.如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P,已知∠ABE=162°,∠DBC=30°,AD=DC=2.5,BC=4.
(1)求∠CBE的度数.
(2)求△CDP与△BEP的周长和.
参考答案与试题解析
一.选择题
1.【解答】解:∵△ABC≌△DEF,
∴BC=EF,
∴BC﹣CE=EF﹣CE,
∴BE=CF,
∵BE=2cm,
∴CF=BE=2cm,
∵BF=8cm,
∴CE=BF﹣BE﹣CF=8﹣2﹣2=4(cm),
故选:B.
2.【解答】解:∵△ABE≌△ACD,
∴AB=AC,BE=CD,AD=AE,∠BAE=∠CAD,
∴∠BAE﹣∠DAE=∠CAD﹣∠DAE,
∴∠BAD=∠CAE,
即只有选项D符合题意,选项A、选项B、选项C都不符合题意;
故选:D.
3.【解答】解:A.∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠BAD=∠CAE,故本选项不符合题意;
B.∵△ABC≌△ADE,
∴∠C=∠E,
∵∠AOE=∠DOC,∠E+∠CAE+∠AOE=180°,∠C+∠COD+∠,CDE=180°,
∴∠CAE=∠CDE,
∵∠BAD=∠CAE,
∴∠BAD=∠CDE,故本选项不符合题意;
C.∵△ABC≌△ADE,
∴∠B=∠ADE,AB=AD,
∴∠B=∠BDA,
∴∠BDA=∠ADE,
∴AD平分∠BDE,故本选项不符合题意;
D.∵△ABC≌△ADE,
∴BC=DE,故本选项符合题意;
故选:D.
4.【解答】解:∵△ABC≌△A'B'C',∠C'=23°,
∴∠C=∠C′=23°,
∵∠A=37°,
∴∠B=180°﹣∠A﹣∠C=180°﹣37°﹣23°=120°,
故选:C.
5.【解答】解:符合要求的条件是①②④,
证明:连接AC、A′C′,
在△ABC与△A′B′C′中,
,
∴△ABC≌△A′B′C′(SAS),
∴AC=A′C′,∠ACB=∠A′C′B′,∠ACB=∠A′C′B′,
∵∠BAD=∠B′A′D′,
∴∠BAD﹣∠DAC=∠B′A′D′﹣∠D′A′C′,
∴∠DAC=∠D′A′C′,
在△ACD和△A′C′D中,
,
∴△ACD≌△A′C′D′(SAS),
∴∠D=∠D′,∠ACD=∠A′C′D′,CD=C′D′,
∴∠BCD=∠B′C′D′,
∴四边形ABCD和四边形A′B′C′D′中,
AB=A′B′,BC=B′C′,AD=A′D′,DC=D′C′,
∠B=∠B′,∠BCD=∠B′C′D′,∠D=∠D′,∠BAD=∠B′A′D′,
∴四边形ABCD≌四边形A′B′C′D′.
同理根据②④的条件证得四边形ABCD≌四边形A′B′C′D′.
故选:B.
6.【解答】解:∵△ABC≌△DEF,
∴BC=EF,
∵BF=BC﹣FC,CE=FE﹣FC,
∴BF=CE,
∵BE=5,CF=2,
∴CF=BE﹣CE﹣BF,即2=5﹣2BF.
∴BF=1.5.
故选:C.
7.【解答】解:∵∠ACB=90°,∠ABC=3 0°,
∴∠A=90°﹣30°=60° ,
∵△ABC≌△A′B′C ,
∴CA′=CA,
∴△ACA′ 为等边三角形,
∴∠ACA′=60° ,
故选:D.
8.【解答】解:在△ABC中,∠A:∠ABC:∠ACB=3:5:10
设∠A=3x°,则∠ABC=5x°,∠ACB=10x°
3x+5x+10x=180
解得x=10
则∠A=30°,∠ABC=50°,∠ACB=100°
∴∠BCN=180°﹣100°=80°
又△MNC≌△ABC
∴∠ACB=∠MCN=100°
∴∠BCM=∠NCM﹣∠BCN=100°﹣80°=20°
∴∠BCM:∠BCN=20°:80°=1:4
故选:D.
9.【解答】解:∵△ABC≌△A′BC′,∠C=25°,
∴∠C=∠C′=25°,∠A′BC′=∠ABC,
∴∠A′BC′﹣∠ABC′=∠ABC﹣∠ABC′,
即∠ABA′=∠CBC′,
∵A′C′∥BC,∠C′=25°,
∴∠CBC′=∠C′=25°,
∴∠ABA′=25°,
故选:C.
10.【解答】解:延长C′D交AB′于H.
∵△AEB≌△AEB′,
∴∠ABE=∠AB′E,
∵C′H∥EB′,
∴∠AHC′=∠AB′E,
∴∠ABE=∠AHC′,
∵△ADC≌△ADC′,
∴∠C′=∠ACD,
∵∠BFC=∠DBF+∠BDF,∠BDF=∠CAD+∠ACD,
∴∠BFC=∠AHC′+∠C′+∠DAC,
∵∠DAC=∠DAC′=∠CAB′=45°,
∴∠C′AH=135°,
∴∠C′+∠AHC′=45°,
∴∠BFC=45°+45°=90°.
故选:A.
二.填空题
.【解答】解:∵△ABD≌△EBC,BC=6,AB=3,
∴BD=BC=6,BE=AB=3,
∴DE=BD﹣BE=6﹣3=3,
故答案为:3.
.【解答】解:∵△ABE≌△DBC,∠DBC=130°,
∴∠ABE=∠DBC=130°,
∴∠ABD+∠DBE+∠EBC+∠DBE=260°,
∵∠ABD+∠DBE+∠EBC=180°,
∴∠DBE=80°,
∴∠EBC=∠DBC﹣∠DBE=130°﹣80°=50°,
∴∠1=180°﹣∠C﹣∠EBC=180°﹣20°﹣50°=110°,
故答案为:110°.
.【解答】解:∵A(﹣6,0),B(0,5),
∴OA=6,OB=5,∠AOB=90°,
∵△OA'B'≌△AOB,
∴OA′=OA=6,A′B′=OB=5,∠B′A′O=90°,
∵点B′在第四象限,
∴点B′的坐标是(6,﹣5),
故答案为:(6,﹣5).
.【解答】解:∵△ABC≌△EDF,
∴∠B=∠EDF,∠C=∠F,
∵∠EDA=20°,∠F=60°,
∴∠B=20°,∠C=60°,
∴∠BAC=180°﹣∠B﹣∠C=100°,
∵AD是∠BAC的平分线,
∴∠DAC=BAC=50°,
故答案为:50°.
.【解答】解:∵△ADE≌△CFE,
∴AD=CF,∠A=∠ECF,AE=CE,
∴AB∥CF,点E是AC的中点
∴①②④正确;
∵∠AED不一定为直角
∴AC⊥DF不一定成立
∴③不正确.
故答案为③.
三.解答题
.【解答】解:(1)∵正五边形的内角和为:(5﹣2)×180°=540°,
∴∠ABC=×540°=108°;
(2)∵△ABF≌△BCG,
∴∠BAF=∠CBG,
∵∠BAF+∠ABH=∠AHG,
∴∠CBH+∠ABH=∠AHG=∠ABC=×540°=108°,
∴∠AHG=108°.
.【解答】(1)证明:∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC﹣∠BAE=∠DAE﹣∠BAE,
∴∠CAE=∠BAD;
(2)解:∵△ABC≌△ADE,
∴∠D=∠B,
∵∠AFD=∠EFB,∠D+∠BAD+∠AFD=180°,∠B+∠EFB+∠BED=180°,
∴∠BED=∠BAD,
∵∠BAD=35°,
∴∠BED=35°.
.【解答】(1)解:DE=CE+BC.
理由:∵△ABC≌△DAE,
∴AE=BC,DE=AC.
∵A,E,C三点在同一直线上,
∴AC=AE+CE,
∴DE=CE+BC;
(2)当△ADE满足∠AED=90°时,DE∥BC,
证明:∵△ABC≌△DAE,∠AED=90°,
∴∠C=∠AED=90°,∠DEC=180°﹣∠AED=90°,
∴∠C=∠DEC.
∴DE∥BC,
即当△ADE满足∠AED=90°时,DE∥BC.
.【解答】(1)证明:∵△ABC≌△DAE,
∴AE=BC,AC=DE,
又∵AE=AC+CE,
∴BC=DE+CE;
(2)解:∵BC∥DE,
∴∠BCE=∠E,
又∵△ABC≌△DAE,
∴∠ACB=∠E,
∴∠ACB=∠BCE,
又∵∠ACB+∠BCE=180°,
∴∠ACB=90°,
即当△ABC满足∠ACB为直角时,BC∥DE.
.【解答】解:(1)∵∠ABE=162°,∠DBC=30°,
∴∠ABD+∠CBE=132°,
∵△ABC≌△DBE,
∴∠ABC=∠DBE,
∴∠ABD=∠CBE=132°÷2=66°,
即∠CBE的度数为66°;
(2)∵△ABC≌△DBE,
∴DE=AC=AD+DC=5,BE=BC=4,
∴△CDP与△BEP的周长和=DC+DP+PC+BP+PE+BE=DC+DE+BC+BE=2.5+5+4+4=15.5.
