2022-2023学年华师大版九年级数学上册23.3 相似三角形 同步练习题 (含答案)
文档属性
| 名称 | 2022-2023学年华师大版九年级数学上册23.3 相似三角形 同步练习题 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 230.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 10:37:37 | ||
图片预览


文档简介
2022-2023学年华东师大版九年级数学上册《23.3相似三角形》同步练习题(附答案)
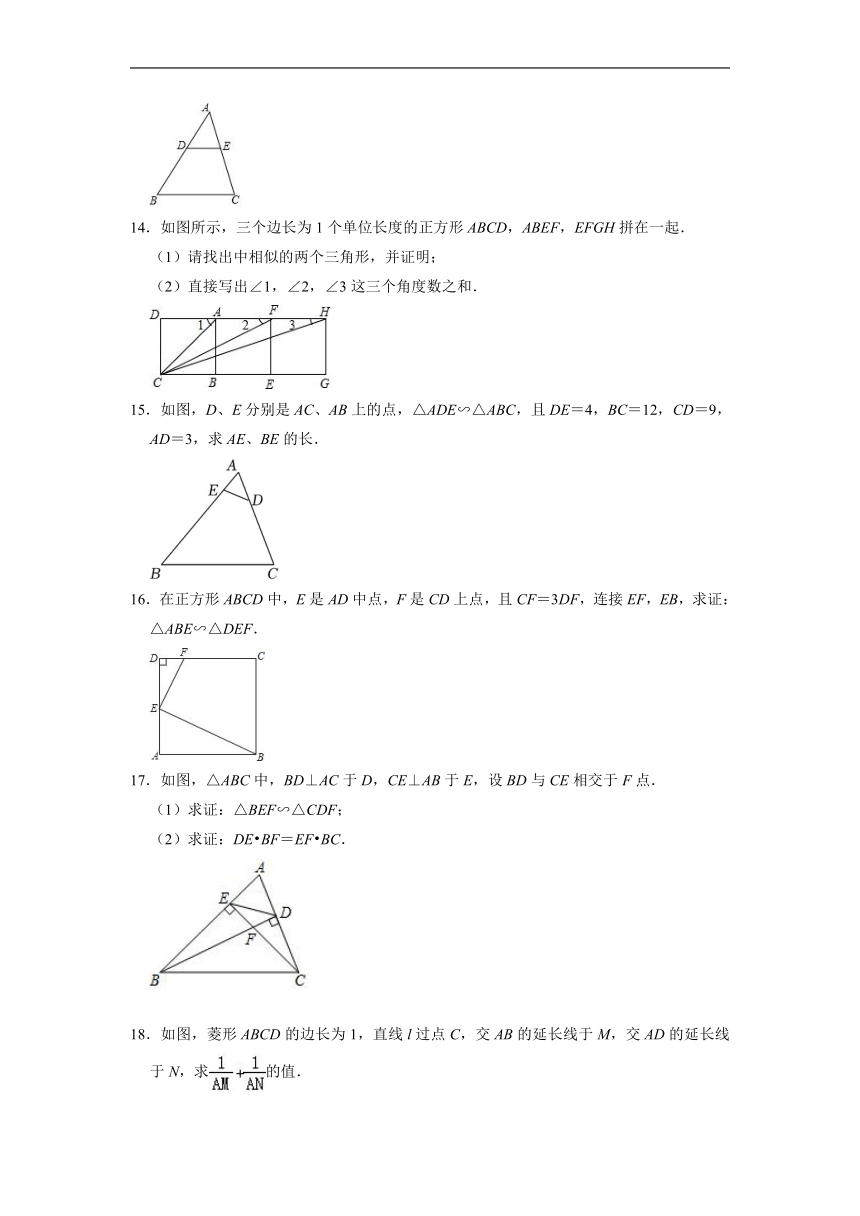
一.选择题
1.若△ABC与△A1B1C1相似且对应中线之比为2:5,则周长之比和面积比分别是( )
A.2:5,4:5 B.2:5,4:25 C.4:25,4:25 D.4:25,2:5
2.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5cm,15cm和18cm,另一个三角形的最长边长为9cm,则它的最短边为( )
A.2cm B.2.5cm C.4cm D.7.5cm
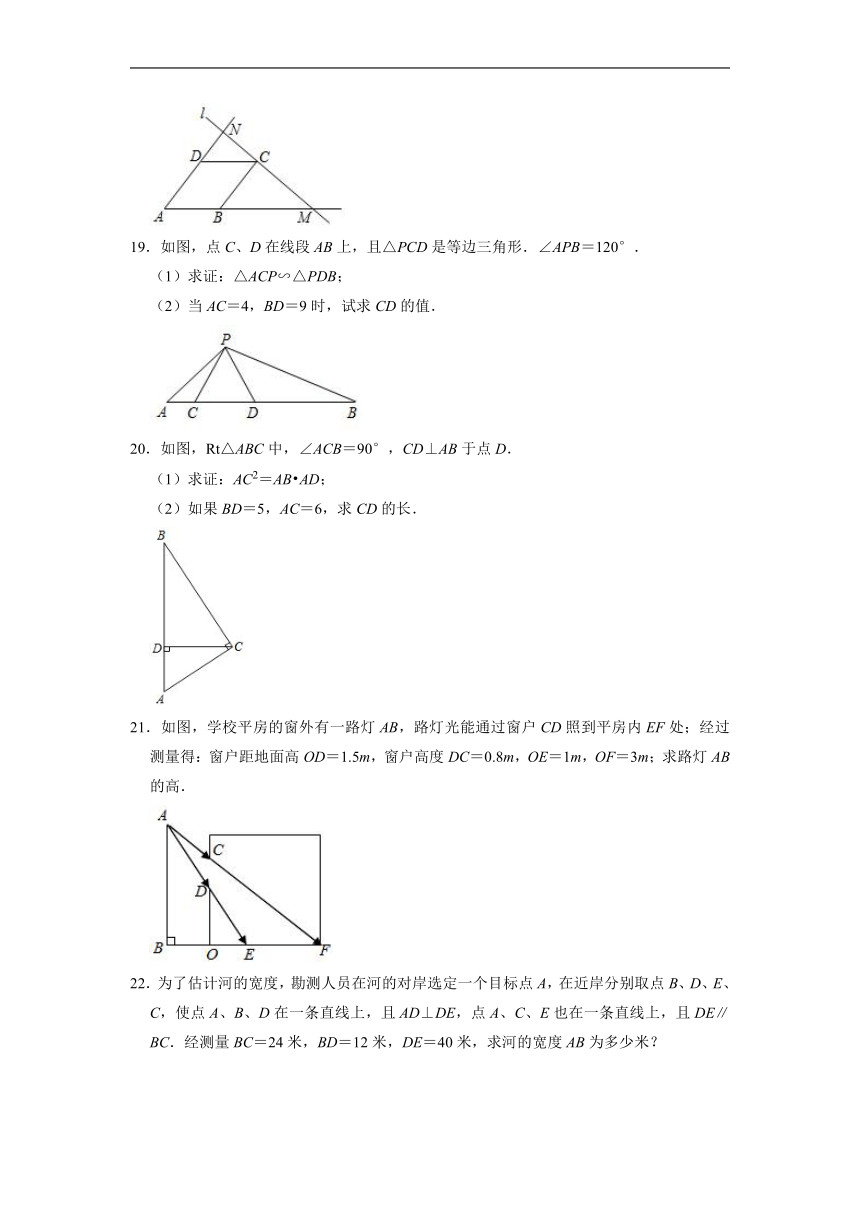
3.如图,下列四个三角形中,与△ABC相似的是( )
A. B. C. D.
4.如图,D是△ABC边AB上一点,添加一个条件后,仍然不能使△ACD∽△ABC的是( )
A.∠ACB=∠ADC B.∠ACD=∠ABC C. D.
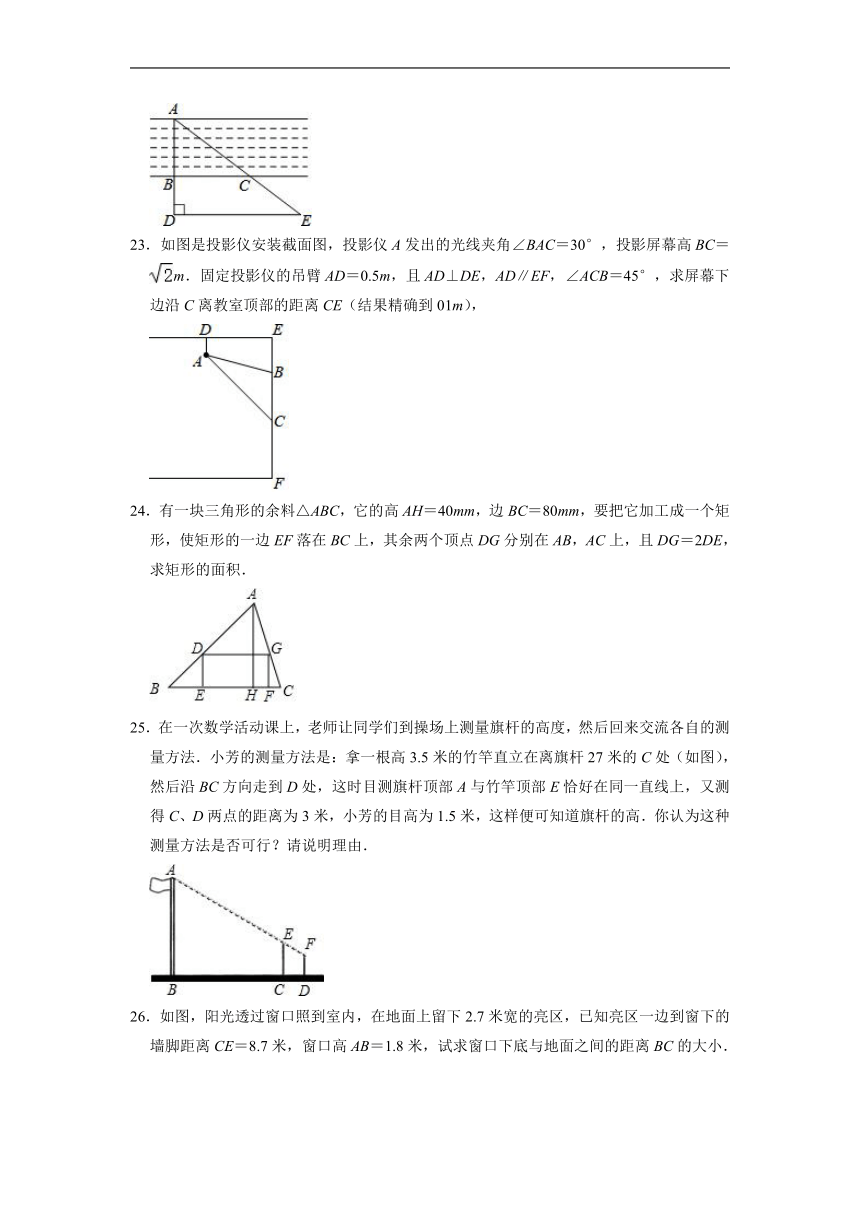
5.如图,在△ABC中,D,E分别是AB,AC的中点,下列说法中不正确的是( )
A.S△ADE:S△ABC=1:2 B.
C.△ADE∽△ABC D.DE=BC
二.填空题
6.两个相似三角形周长的差是4,对应中线的比是4:5,那么较大三角形的周长是 .
7.已知两个相似三角形对应角平分线的比为4:5,周长和为18cm,那么这两个三角形的周长分别是 .
8.一根长为a(cm)的铁丝,首尾相接围成一个等边三角形.要将它按如图的方式向外等距扩1(cm).得到新的等边三角形,则新的等边三角形的周长是 cm.
9.如图,∠1=∠2,若△ABC∽△ADE,可添加的一个条件是 (填写一个条件即可)
10.△ABC的三边长分别为7、6、2,△DEF的两边分别为1、3,要使△ABC∽△DEF,则△DEF的第三边长为 .
三.解答题
11.如图△ABC∽△ACD,∠D=90°,AC=,AD=2,求AB及BC的长.
12.如图,已知△ADE∽△AFG∽△ABC,且△ABC的面积被线段DE、FG三等分,其中BC=12cm,求线段DE和FG的长度.
13.如图.已知△ABC中,△ADE∽△ABC,AD:BD=3:4,求S△ADE:S四边形DECB.
14.如图所示,三个边长为1个单位长度的正方形ABCD,ABEF,EFGH拼在一起.
(1)请找出中相似的两个三角形,并证明;
(2)直接写出∠1,∠2,∠3这三个角度数之和.
15.如图,D、E分别是AC、AB上的点,△ADE∽△ABC,且DE=4,BC=12,CD=9,AD=3,求AE、BE的长.
16.在正方形ABCD中,E是AD中点,F是CD上点,且CF=3DF,连接EF,EB,求证:△ABE∽△DEF.
17.如图,△ABC中,BD⊥AC于D,CE⊥AB于E,设BD与CE相交于F点.
(1)求证:△BEF∽△CDF;
(2)求证:DE BF=EF BC.
18.如图,菱形ABCD的边长为1,直线l过点C,交AB的延长线于M,交AD的延长线于N,求的值.
19.如图,点C、D在线段AB上,且△PCD是等边三角形.∠APB=120°.
(1)求证:△ACP∽△PDB;
(2)当AC=4,BD=9时,试求CD的值.
20.如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D.
(1)求证:AC2=AB AD;
(2)如果BD=5,AC=6,求CD的长.
21.如图,学校平房的窗外有一路灯AB,路灯光能通过窗户CD照到平房内EF处;经过测量得:窗户距地面高OD=1.5m,窗户高度DC=0.8m,OE=1m,OF=3m;求路灯AB的高.
22.为了估计河的宽度,勘测人员在河的对岸选定一个目标点A,在近岸分别取点B、D、E、C,使点A、B、D在一条直线上,且AD⊥DE,点A、C、E也在一条直线上,且DE∥BC.经测量BC=24米,BD=12米,DE=40米,求河的宽度AB为多少米?
23.如图是投影仪安装截面图,投影仪A发出的光线夹角∠BAC=30°,投影屏幕高BC=m.固定投影仪的吊臂AD=0.5m,且AD⊥DE,AD∥EF,∠ACB=45°,求屏幕下边沿C离教室顶部的距离CE(结果精确到01m),
24.有一块三角形的余料△ABC,它的高AH=40mm,边BC=80mm,要把它加工成一个矩形,使矩形的一边EF落在BC上,其余两个顶点DG分别在AB,AC上,且DG=2DE,求矩形的面积.
25.在一次数学活动课上,老师让同学们到操场上测量旗杆的高度,然后回来交流各自的测量方法.小芳的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图),然后沿BC方向走到D处,这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上,又测得C、D两点的距离为3米,小芳的目高为1.5米,这样便可知道旗杆的高.你认为这种测量方法是否可行?请说明理由.
26.如图,阳光透过窗口照到室内,在地面上留下2.7米宽的亮区,已知亮区一边到窗下的墙脚距离CE=8.7米,窗口高AB=1.8米,试求窗口下底与地面之间的距离BC的大小.
27.《九章算术》勾股章:今有木去人不知远近.立四表,相去各一丈,另左两表与所望参相直,从后右表望之,入前右表三寸,问:木去人几何?用今天的话说,大意是:如图,前方P处有树木,距人B处不知远近,先画正方形ABCD,边长为1丈,从左边看,P、A、B在同一直线上,从右边看,PC交AD于点E,并且DE的长为3寸,试求树木与人的距离.(精确到0.1尺,提示:1丈=10尺,1尺=10寸.)
参考答案
一.选择题
1.解:∵△ABC与△A1B1C1相似,且对应中线之比为2:5,
∴其相似比为2:5,
∴△ABC与△A1B1C1周长之比为2:5,
△ABC与△A1B1C1面积比为4:25,
故选:B.
2.解:设另一个三角形的最短边长为xcm,
根据题意,得:,
解得:x=2.5,
即另一个三角形的最短边的长为2.5cm.
故选:B.
3.解:∵由图可知,AB=AC=6,∠B=75°,
∴∠C=75°,∠A=30°,
A、三角形各角的度数分别为75°,52.5°,52.5°,
B、三角形各角的度数都是60°,
C、三角形各角的度数分别为75°,30°,75°,
D、三角形各角的度数分别为40°,70°,70°,
∴只有C选项中三角形各角的度数与题干中三角形各角的度数相等,
故选:C.
4.解:A、当∠ACB=∠ADC时,再由∠A=∠A,可得出△ACD∽△ABC,故此选项不合题意;
B、当∠ACD=∠ABC时,再由∠A=∠A,可得出△ACD∽△ABC,故此选项不合题意;
C、当=时,再由∠A=∠A,可得出△ACD∽△ABC,故此选项不合题意;
D、当=时,无法得出△ACD∽△ABC,故此选项符合题意;
故选:D.
5.解:∵D,E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,===,
∴△ADE∽△ABC,DE=BC,
∴=()2=()2=.
故选:A.
二.填空题
6.解:令较大的三角形的周长为x.
小三角形的周长为x﹣4,
由两个相似三角形对应中线的比为4:5得,
4:5=(x﹣4):x,
解之得x=20.
故答案为20.
7.解:设其中一个三角形的周长为xcm,则另一个三角形的周长为(18﹣x)cm,
∵两个相似三角形对应角平分线的比为4:5,
∴两个相似三角形的相似比为4:5,
∴两个相似三角形的周长比为4:5,
∴=,
解得,x=8,
则18﹣x=10,
故答案为:8cm、10cm.
8.解:如图,在Rt△ABC中,
∵AC=1,∠ACB=90°,∠ABC=30°,
∴BC=,
∴新的等边三角形的周长是(a+6)cm,
故答案为:a+6.
9.解:∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,
即∠BAC=∠DAE,
所以,添加的条件为∠D=∠B或∠C=∠AED或.
故答案为:∠D=∠B或∠C=∠AED或.
10.解:∵要使△ABC∽△DEF,需,
∵△ABC的三边长分别为7、6、2,△DEF的两边分别为1、3,
∴△DEF的两边1、3分别与△ABC的两边2,6是对应边,
∴△DEF的第三边长为:7×=3.5.
故答案为:3.5.
三.解答题
11.解:∵△ABC∽△ACD,
∴,
∵AC=,AD=2,
∴,
解得:AB=2.5,
∵∠D=90°,
∴∠ACB=∠D=90°,
∴BC==.
12.解:∵△ADE∽△ABC,且△ABC的面积被线段DE、FG三等分,
∴()2=,
即()2=,
解得DE=4,
∵△AFG∽△ABC,且△ABC的面积被线段DE、FG三等分,
∴()2=,
即()2=,
解得FG=4,
答:线段DE和FG的长度分别为4cm,4cm.
13.解:∵△ADE∽△ABC,AD:BD=3:4,
∴=,
∴=,
∴S△ADE:S四边形DECB=9:40.
14.解:(1)ACF∽△AHC.理由如下:
∵AC=,AF=1,AH=2,
∴==,
而∠FAC=∠CAH,
∴△ACF∽△AHC;
(2)∵△ACF∽△AHC
∴∠2=∠ACH,
而∠1=∠ACH+∠3,
∴∠1=∠2+∠3.
∵∠1=45°,
∴∠1+∠2+∠3=90°.
15.解:∵△ADE∽△ABC,
∴==,
∵DE=4,BC=12,CD=9,AD=3,
∴AC=AD+CD=12,
∴AE=4,AB=9,
∴BE=AB﹣AE=5.
16.证明:∵四边形ABCD是正方形,
∴AD=AB=DC,∠A=∠D=90°,
∵E是AD中点,
∴=,
∵CF=3DF,
∴=,
∴=,
∴△ABE∽△DEF.
17.证明:(1)∵BD⊥AC,CE⊥AB,
∴∠BEF=∠CDF=90°,且∠EFB=∠DFC,
∴△BEF∽△CDF;
(2)∵∠BEF=∠CDF=90°,
∴点B,点C,点D,点E四点共圆,
∴∠DEF=∠DBC,∠BFC=∠DFE,
∴△DEF∽△CBF,
∴,
∴DE BF=EF BC
18.解:∵四边形ABCD是菱形,
∴BC∥AD
∴=
∵CD∥AB
∴=
∴+=+=1
又∵AB=AD=1,
∴+=1.
答:的值为1.
19.(1)证明:∵△PCD为等边三角形,
∴∠PCD=∠PDC=60°.
∴∠ACP=∠PDB=120°.
∵∠APB=120°,
∴∠A+∠B=60°.
∵∠PDB=120°,
∴∠DPB+∠B=60°.
∴∠A=∠DPB.
∴△ACP∽△PDB.
(2)解:由(1)得△ACP∽△PDB,
∴,
∵△PCD是等边三角形,
∴PC=PD=CD,
∴,
∴CD2=AC BD.
∵AC=4,BD=9,
∴CD=6.
20.(1)证明:∵CD⊥AB,
∴∠ADC=90°,
∵∠DAC=∠CAB,
∴Rt△ACD∽Rt△ABC,
∴AC:AB=AD:AC,
∴AC2=AB AD;
(2)解:∵AC2=AB AD,
∴62=(AD+5) AD,
整理得AD2+5AD﹣36=0,解得AD=﹣9(舍去)或AD=4,
∵CD2=AD BD,
∴CD==2.
21.解:连接DC,
设:路灯AB高为x米,BO的长度为y米,
由中心投影可知△ABE∽△DOE,
∴,
∵△ABF∽△COF,
∴
∴,
解得
答:路灯AB的高度为米.
22.解:设宽度AB为x米,
∵DE∥BC,
∴△ABC∽△ADE,
∴=,
又∵BC=24,BD=12,DE=40,
∴=,
解得x=18,
答:河的宽度为18米.
23.解:过B作BH⊥AC于H,过A作AP⊥EF于P,
∴PE=AD=0.5,
在Rt△BCH中,BC=,∠ACB=45°,
∴BH=HC=1,
在Rt△ABH中,∠BAH=30°,
∴AH=,
∴AC=+1,
∴PC=(+1),
∴CE=(+1)+0.5≈2.4m.
答:屏幕下边沿C离教室顶部的距离CE为2.4m.
24.解:如图,设AH交DG于点K.设DE=x,则DG=2x,
∵DG∥BC,
∴△ADG∽△ABC,
∴=,即=,解得x=20,
∴2x=40,
即DE=x,DG=40,
∴矩形EFGD的面积为40×20=800(mm2).
答:矩形的面积为800mm2.
25.解:这种测量方法可行.
理由如下:
设旗杆高AB=x.过F作FG⊥AB于G,交CE于H(如图).
所以△AGF∽△EHF.
因为FD=1.5,GF=27+3=30,HF=3,
所以EH=3.5﹣1.5=2,AG=x﹣1.5.
由△AGF∽△EHF,
得=,
即=,
所以x﹣1.5=20,
解得x=21.5(米)
答:旗杆的高为21.5米.
26.解:∵光是沿直线传播的,
∴BD∥AE,
∴△CBD∽△CAE,
∴=,
即=,
解得BC=4.
27.解;∵正方形ABCD,边长为1丈.
∴AB=AD=CD=10寸
∵DE=3寸=0.3尺,
AE=10﹣0.3=9.7(尺),
又∵AB∥CD,
∴PA∥CD,
∴△PAE∽△CDE,
∴=,
∴=,
∴PA≈323.3,
∴PB=PA+AB=323.3+10=333.3
答:树木与人的距离约为333.3尺.
一.选择题
1.若△ABC与△A1B1C1相似且对应中线之比为2:5,则周长之比和面积比分别是( )
A.2:5,4:5 B.2:5,4:25 C.4:25,4:25 D.4:25,2:5
2.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5cm,15cm和18cm,另一个三角形的最长边长为9cm,则它的最短边为( )
A.2cm B.2.5cm C.4cm D.7.5cm
3.如图,下列四个三角形中,与△ABC相似的是( )
A. B. C. D.
4.如图,D是△ABC边AB上一点,添加一个条件后,仍然不能使△ACD∽△ABC的是( )
A.∠ACB=∠ADC B.∠ACD=∠ABC C. D.
5.如图,在△ABC中,D,E分别是AB,AC的中点,下列说法中不正确的是( )
A.S△ADE:S△ABC=1:2 B.
C.△ADE∽△ABC D.DE=BC
二.填空题
6.两个相似三角形周长的差是4,对应中线的比是4:5,那么较大三角形的周长是 .
7.已知两个相似三角形对应角平分线的比为4:5,周长和为18cm,那么这两个三角形的周长分别是 .
8.一根长为a(cm)的铁丝,首尾相接围成一个等边三角形.要将它按如图的方式向外等距扩1(cm).得到新的等边三角形,则新的等边三角形的周长是 cm.
9.如图,∠1=∠2,若△ABC∽△ADE,可添加的一个条件是 (填写一个条件即可)
10.△ABC的三边长分别为7、6、2,△DEF的两边分别为1、3,要使△ABC∽△DEF,则△DEF的第三边长为 .
三.解答题
11.如图△ABC∽△ACD,∠D=90°,AC=,AD=2,求AB及BC的长.
12.如图,已知△ADE∽△AFG∽△ABC,且△ABC的面积被线段DE、FG三等分,其中BC=12cm,求线段DE和FG的长度.
13.如图.已知△ABC中,△ADE∽△ABC,AD:BD=3:4,求S△ADE:S四边形DECB.
14.如图所示,三个边长为1个单位长度的正方形ABCD,ABEF,EFGH拼在一起.
(1)请找出中相似的两个三角形,并证明;
(2)直接写出∠1,∠2,∠3这三个角度数之和.
15.如图,D、E分别是AC、AB上的点,△ADE∽△ABC,且DE=4,BC=12,CD=9,AD=3,求AE、BE的长.
16.在正方形ABCD中,E是AD中点,F是CD上点,且CF=3DF,连接EF,EB,求证:△ABE∽△DEF.
17.如图,△ABC中,BD⊥AC于D,CE⊥AB于E,设BD与CE相交于F点.
(1)求证:△BEF∽△CDF;
(2)求证:DE BF=EF BC.
18.如图,菱形ABCD的边长为1,直线l过点C,交AB的延长线于M,交AD的延长线于N,求的值.
19.如图,点C、D在线段AB上,且△PCD是等边三角形.∠APB=120°.
(1)求证:△ACP∽△PDB;
(2)当AC=4,BD=9时,试求CD的值.
20.如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D.
(1)求证:AC2=AB AD;
(2)如果BD=5,AC=6,求CD的长.
21.如图,学校平房的窗外有一路灯AB,路灯光能通过窗户CD照到平房内EF处;经过测量得:窗户距地面高OD=1.5m,窗户高度DC=0.8m,OE=1m,OF=3m;求路灯AB的高.
22.为了估计河的宽度,勘测人员在河的对岸选定一个目标点A,在近岸分别取点B、D、E、C,使点A、B、D在一条直线上,且AD⊥DE,点A、C、E也在一条直线上,且DE∥BC.经测量BC=24米,BD=12米,DE=40米,求河的宽度AB为多少米?
23.如图是投影仪安装截面图,投影仪A发出的光线夹角∠BAC=30°,投影屏幕高BC=m.固定投影仪的吊臂AD=0.5m,且AD⊥DE,AD∥EF,∠ACB=45°,求屏幕下边沿C离教室顶部的距离CE(结果精确到01m),
24.有一块三角形的余料△ABC,它的高AH=40mm,边BC=80mm,要把它加工成一个矩形,使矩形的一边EF落在BC上,其余两个顶点DG分别在AB,AC上,且DG=2DE,求矩形的面积.
25.在一次数学活动课上,老师让同学们到操场上测量旗杆的高度,然后回来交流各自的测量方法.小芳的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图),然后沿BC方向走到D处,这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上,又测得C、D两点的距离为3米,小芳的目高为1.5米,这样便可知道旗杆的高.你认为这种测量方法是否可行?请说明理由.
26.如图,阳光透过窗口照到室内,在地面上留下2.7米宽的亮区,已知亮区一边到窗下的墙脚距离CE=8.7米,窗口高AB=1.8米,试求窗口下底与地面之间的距离BC的大小.
27.《九章算术》勾股章:今有木去人不知远近.立四表,相去各一丈,另左两表与所望参相直,从后右表望之,入前右表三寸,问:木去人几何?用今天的话说,大意是:如图,前方P处有树木,距人B处不知远近,先画正方形ABCD,边长为1丈,从左边看,P、A、B在同一直线上,从右边看,PC交AD于点E,并且DE的长为3寸,试求树木与人的距离.(精确到0.1尺,提示:1丈=10尺,1尺=10寸.)
参考答案
一.选择题
1.解:∵△ABC与△A1B1C1相似,且对应中线之比为2:5,
∴其相似比为2:5,
∴△ABC与△A1B1C1周长之比为2:5,
△ABC与△A1B1C1面积比为4:25,
故选:B.
2.解:设另一个三角形的最短边长为xcm,
根据题意,得:,
解得:x=2.5,
即另一个三角形的最短边的长为2.5cm.
故选:B.
3.解:∵由图可知,AB=AC=6,∠B=75°,
∴∠C=75°,∠A=30°,
A、三角形各角的度数分别为75°,52.5°,52.5°,
B、三角形各角的度数都是60°,
C、三角形各角的度数分别为75°,30°,75°,
D、三角形各角的度数分别为40°,70°,70°,
∴只有C选项中三角形各角的度数与题干中三角形各角的度数相等,
故选:C.
4.解:A、当∠ACB=∠ADC时,再由∠A=∠A,可得出△ACD∽△ABC,故此选项不合题意;
B、当∠ACD=∠ABC时,再由∠A=∠A,可得出△ACD∽△ABC,故此选项不合题意;
C、当=时,再由∠A=∠A,可得出△ACD∽△ABC,故此选项不合题意;
D、当=时,无法得出△ACD∽△ABC,故此选项符合题意;
故选:D.
5.解:∵D,E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,===,
∴△ADE∽△ABC,DE=BC,
∴=()2=()2=.
故选:A.
二.填空题
6.解:令较大的三角形的周长为x.
小三角形的周长为x﹣4,
由两个相似三角形对应中线的比为4:5得,
4:5=(x﹣4):x,
解之得x=20.
故答案为20.
7.解:设其中一个三角形的周长为xcm,则另一个三角形的周长为(18﹣x)cm,
∵两个相似三角形对应角平分线的比为4:5,
∴两个相似三角形的相似比为4:5,
∴两个相似三角形的周长比为4:5,
∴=,
解得,x=8,
则18﹣x=10,
故答案为:8cm、10cm.
8.解:如图,在Rt△ABC中,
∵AC=1,∠ACB=90°,∠ABC=30°,
∴BC=,
∴新的等边三角形的周长是(a+6)cm,
故答案为:a+6.
9.解:∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,
即∠BAC=∠DAE,
所以,添加的条件为∠D=∠B或∠C=∠AED或.
故答案为:∠D=∠B或∠C=∠AED或.
10.解:∵要使△ABC∽△DEF,需,
∵△ABC的三边长分别为7、6、2,△DEF的两边分别为1、3,
∴△DEF的两边1、3分别与△ABC的两边2,6是对应边,
∴△DEF的第三边长为:7×=3.5.
故答案为:3.5.
三.解答题
11.解:∵△ABC∽△ACD,
∴,
∵AC=,AD=2,
∴,
解得:AB=2.5,
∵∠D=90°,
∴∠ACB=∠D=90°,
∴BC==.
12.解:∵△ADE∽△ABC,且△ABC的面积被线段DE、FG三等分,
∴()2=,
即()2=,
解得DE=4,
∵△AFG∽△ABC,且△ABC的面积被线段DE、FG三等分,
∴()2=,
即()2=,
解得FG=4,
答:线段DE和FG的长度分别为4cm,4cm.
13.解:∵△ADE∽△ABC,AD:BD=3:4,
∴=,
∴=,
∴S△ADE:S四边形DECB=9:40.
14.解:(1)ACF∽△AHC.理由如下:
∵AC=,AF=1,AH=2,
∴==,
而∠FAC=∠CAH,
∴△ACF∽△AHC;
(2)∵△ACF∽△AHC
∴∠2=∠ACH,
而∠1=∠ACH+∠3,
∴∠1=∠2+∠3.
∵∠1=45°,
∴∠1+∠2+∠3=90°.
15.解:∵△ADE∽△ABC,
∴==,
∵DE=4,BC=12,CD=9,AD=3,
∴AC=AD+CD=12,
∴AE=4,AB=9,
∴BE=AB﹣AE=5.
16.证明:∵四边形ABCD是正方形,
∴AD=AB=DC,∠A=∠D=90°,
∵E是AD中点,
∴=,
∵CF=3DF,
∴=,
∴=,
∴△ABE∽△DEF.
17.证明:(1)∵BD⊥AC,CE⊥AB,
∴∠BEF=∠CDF=90°,且∠EFB=∠DFC,
∴△BEF∽△CDF;
(2)∵∠BEF=∠CDF=90°,
∴点B,点C,点D,点E四点共圆,
∴∠DEF=∠DBC,∠BFC=∠DFE,
∴△DEF∽△CBF,
∴,
∴DE BF=EF BC
18.解:∵四边形ABCD是菱形,
∴BC∥AD
∴=
∵CD∥AB
∴=
∴+=+=1
又∵AB=AD=1,
∴+=1.
答:的值为1.
19.(1)证明:∵△PCD为等边三角形,
∴∠PCD=∠PDC=60°.
∴∠ACP=∠PDB=120°.
∵∠APB=120°,
∴∠A+∠B=60°.
∵∠PDB=120°,
∴∠DPB+∠B=60°.
∴∠A=∠DPB.
∴△ACP∽△PDB.
(2)解:由(1)得△ACP∽△PDB,
∴,
∵△PCD是等边三角形,
∴PC=PD=CD,
∴,
∴CD2=AC BD.
∵AC=4,BD=9,
∴CD=6.
20.(1)证明:∵CD⊥AB,
∴∠ADC=90°,
∵∠DAC=∠CAB,
∴Rt△ACD∽Rt△ABC,
∴AC:AB=AD:AC,
∴AC2=AB AD;
(2)解:∵AC2=AB AD,
∴62=(AD+5) AD,
整理得AD2+5AD﹣36=0,解得AD=﹣9(舍去)或AD=4,
∵CD2=AD BD,
∴CD==2.
21.解:连接DC,
设:路灯AB高为x米,BO的长度为y米,
由中心投影可知△ABE∽△DOE,
∴,
∵△ABF∽△COF,
∴
∴,
解得
答:路灯AB的高度为米.
22.解:设宽度AB为x米,
∵DE∥BC,
∴△ABC∽△ADE,
∴=,
又∵BC=24,BD=12,DE=40,
∴=,
解得x=18,
答:河的宽度为18米.
23.解:过B作BH⊥AC于H,过A作AP⊥EF于P,
∴PE=AD=0.5,
在Rt△BCH中,BC=,∠ACB=45°,
∴BH=HC=1,
在Rt△ABH中,∠BAH=30°,
∴AH=,
∴AC=+1,
∴PC=(+1),
∴CE=(+1)+0.5≈2.4m.
答:屏幕下边沿C离教室顶部的距离CE为2.4m.
24.解:如图,设AH交DG于点K.设DE=x,则DG=2x,
∵DG∥BC,
∴△ADG∽△ABC,
∴=,即=,解得x=20,
∴2x=40,
即DE=x,DG=40,
∴矩形EFGD的面积为40×20=800(mm2).
答:矩形的面积为800mm2.
25.解:这种测量方法可行.
理由如下:
设旗杆高AB=x.过F作FG⊥AB于G,交CE于H(如图).
所以△AGF∽△EHF.
因为FD=1.5,GF=27+3=30,HF=3,
所以EH=3.5﹣1.5=2,AG=x﹣1.5.
由△AGF∽△EHF,
得=,
即=,
所以x﹣1.5=20,
解得x=21.5(米)
答:旗杆的高为21.5米.
26.解:∵光是沿直线传播的,
∴BD∥AE,
∴△CBD∽△CAE,
∴=,
即=,
解得BC=4.
27.解;∵正方形ABCD,边长为1丈.
∴AB=AD=CD=10寸
∵DE=3寸=0.3尺,
AE=10﹣0.3=9.7(尺),
又∵AB∥CD,
∴PA∥CD,
∴△PAE∽△CDE,
∴=,
∴=,
∴PA≈323.3,
∴PB=PA+AB=323.3+10=333.3
答:树木与人的距离约为333.3尺.
