2022-2023学年人教版八年级数学上册第一次阶段性(11.1—12.3)综合训练题(含解析)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册第一次阶段性(11.1—12.3)综合训练题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 143.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 10:45:52 | ||
图片预览



文档简介
2022-2023学年人教版八年级数学上册第一次阶段性(11.1—12.3)综合训练题(附答案)
一、选择题(每题3分,共36分)
1.下列每组数分别表示三根木棒的长度,将它们首尾连接后,能摆成三角形的一组是( )
A.1,2,6 B.2,2,4 C.1,2,3 D.2,3,4
2.图中能表示△ABC的BC边上的高的是( )
A. B.
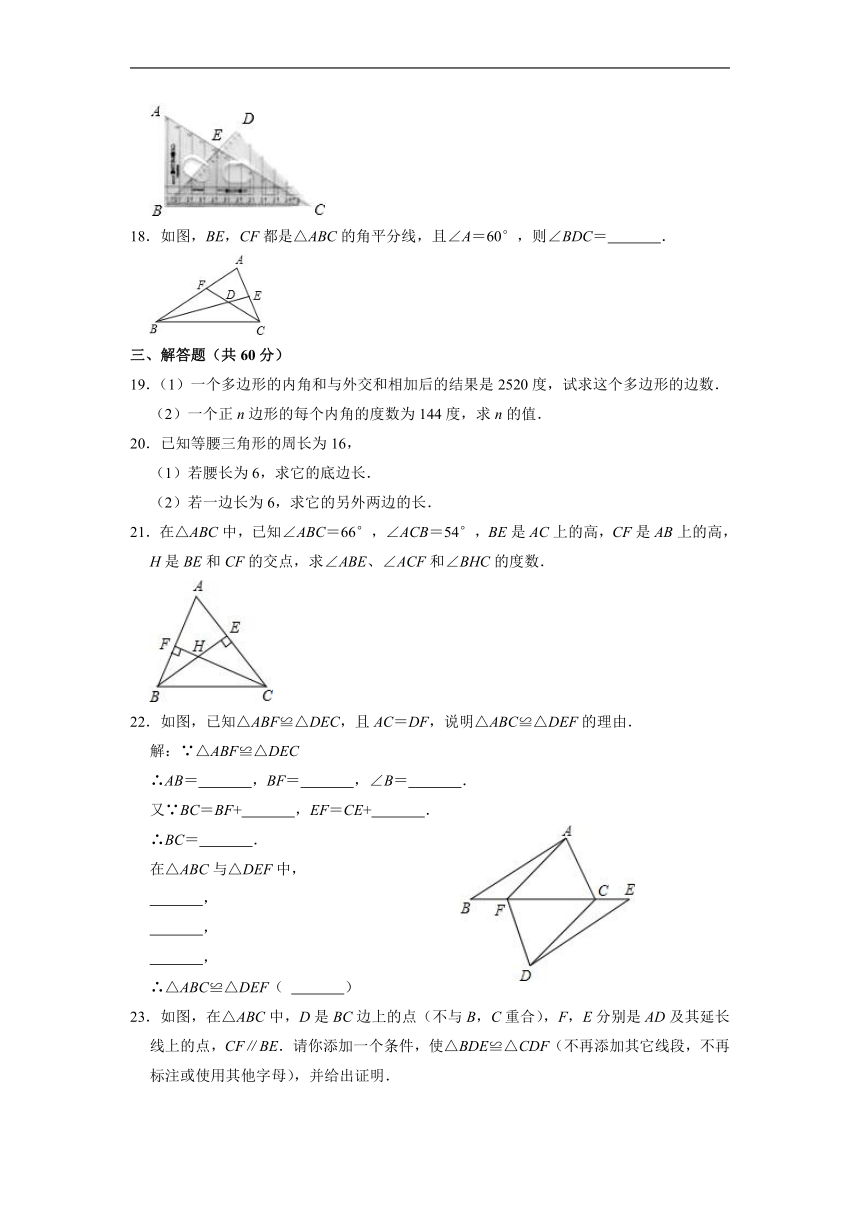
C. D.
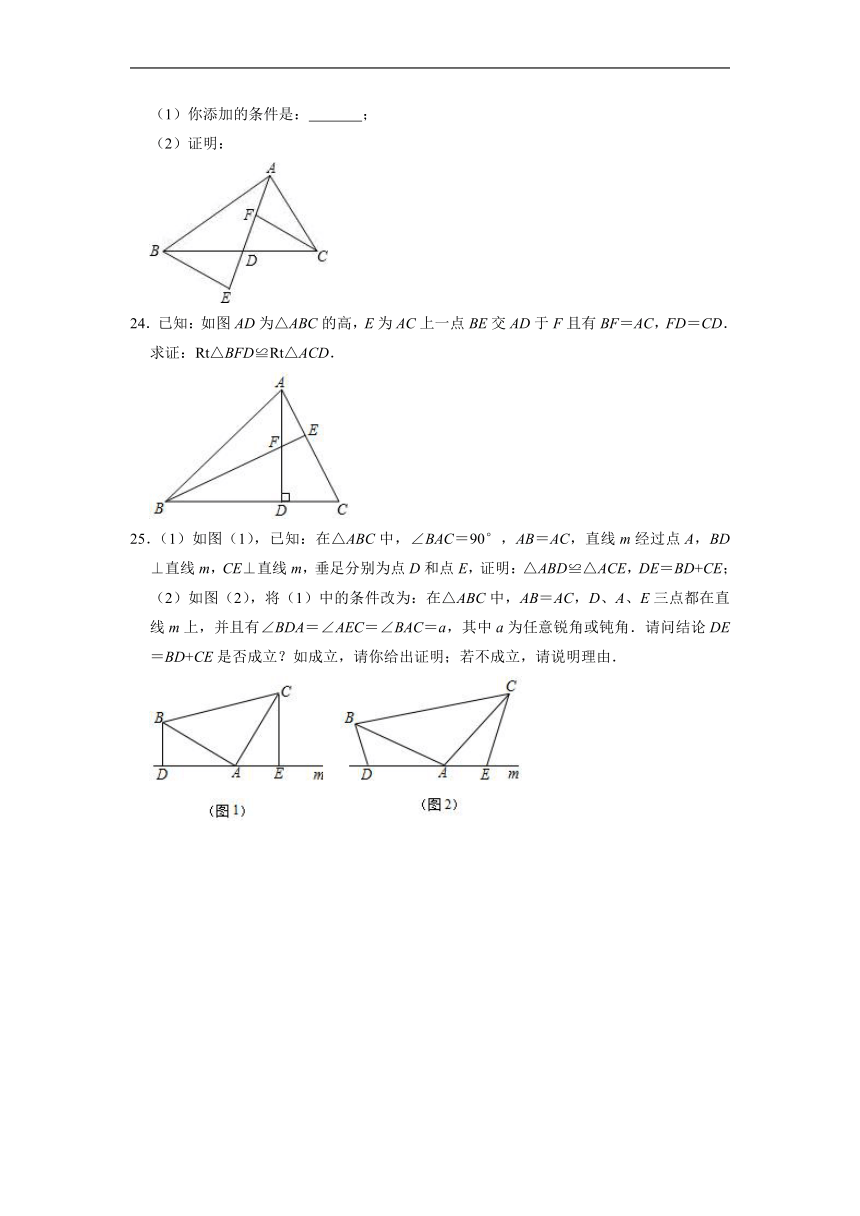
3.能将三角形的面积平分的是三角形的( )
A.三条中线 B.三条高
C.三条角平分线 D.三边的垂直平分线
4.下列说法正确的是( )
A.形状相同的两个三角形全等 B.面积相等的两个三角形全等
C.完全重合的两个三角形全等 D.所有的等边三角形全等
5.在下列条件中:①∠A+∠B=∠C;②∠A=∠B=2∠C;③∠A:∠B:∠C=1:2:3,能确定△ABC为直角三角形的条件有( )
A.1个 B.2个 C.3个 D.0个
6.一等腰三角形的两边长分别为4和8,则这个等腰三角形的周长为( )
A.16 B.20 C.18 D.16或20
7.一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )
A.108° B.90° C.72° D.60°
8.已知△ABC的六个元素如图,则甲、乙、丙三个三角形中和△ABC全等的图形是( )
A.甲、乙 B.乙、丙 C.只有乙 D.只有丙
9.如图,∠ACD是△ABC的外角,若∠ACD=110°,∠B=50°,则∠A=( )
A.40° B.50° C.55° D.60°
10.如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=12,AC=8,则CD的长为( )
A.5.5 B.4 C.4.5 D.3
11.从多边形一条边上的一点(不是顶点)出发,连接各个顶点得到2013个三角形,则这个多边形的边数为( )
A.2011 B.2015 C.2014 D.2016
12.如图,AD是△ABC的中线,E、F分别是AD和AD延长线上的点,且DE=DF,连接BF、CE,下列说法:①CE=BF;②△ABD和△ACD的面积相等;③BF∥CE;④△BDF≌△CDE,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每题4分,共24分)
13.生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有 性.
14.如果三角形的两边长分别是3和5,那么它的第三边x的取值范围是 .
15.已知在△ABC中,∠A=40°,∠B﹣∠C=40°,则∠B= ,∠C= .
16.等腰三角形一腰上的中线将其周长分为15和12两部分,则它的底边长是 .
17.如图是一副三角尺拼成的图案,则∠CEB= °.
18.如图,BE,CF都是△ABC的角平分线,且∠A=60°,则∠BDC= .
三、解答题(共60分)
19.(1)一个多边形的内角和与外交和相加后的结果是2520度,试求这个多边形的边数.
(2)一个正n边形的每个内角的度数为144度,求n的值.
20.已知等腰三角形的周长为16,
(1)若腰长为6,求它的底边长.
(2)若一边长为6,求它的另外两边的长.
21.在△ABC中,已知∠ABC=66°,∠ACB=54°,BE是AC上的高,CF是AB上的高,H是BE和CF的交点,求∠ABE、∠ACF和∠BHC的度数.
22.如图,已知△ABF≌△DEC,且AC=DF,说明△ABC≌△DEF的理由.
解:∵△ABF≌△DEC
∴AB= ,BF= ,∠B= .
又∵BC=BF+ ,EF=CE+ .
∴BC= .
在△ABC与△DEF中,
,
,
,
∴△ABC≌△DEF( )
23.如图,在△ABC中,D是BC边上的点(不与B,C重合),F,E分别是AD及其延长线上的点,CF∥BE.请你添加一个条件,使△BDE≌△CDF(不再添加其它线段,不再标注或使用其他字母),并给出证明.
(1)你添加的条件是: ;
(2)证明:
24.已知:如图AD为△ABC的高,E为AC上一点BE交AD于F且有BF=AC,FD=CD.
求证:Rt△BFD≌Rt△ACD.
25.(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D和点E,证明:△ABD≌△ACE,DE=BD+CE;
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=a,其中a为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
参考答案
一、选择题(每题3分,共36分)
1.解:A、1+2<6,不能组成三角形,故此选项错误;
B、2+2=4,不能组成三角形,故此选项错误;
C、1+2=3,不能组成三角形,故此选项错误;
D、2+3>4,能组成三角形,故此选项正确;
故选:D.
2.解:题中需要画△ABC的BC边上的高.应当过顶点A向BC边作垂线,顶点A到垂足E的垂线段就为BC边上的高.钝角三角形钝角两夹边的高在三角形的外部.
故选:D.
3.解:三角形的中线将三角形分成面积相等的两部分.
故选:A.
4.解:A、形状相同的两个三角形全等,说法错误,应该是形状相同且大小也相同的两个三角形全等;
B、面积相等的两个三角形全等,说法错误;
C、完全重合的两个三角形全等,说法正确;
D、所有的等边三角形全等,说法错误;
故选:C.
5.解:∵∠A+∠B+∠C=180°,
∴若 ①∠A+∠B=∠C,则∠C=90°.三角形为直角三角形;
②∠A=∠B=2∠C,则∠A=∠B=72°,∠C=36°.三角形不是直角三角形;
③∠A:∠B:∠C=1:2:3,则∠A=30°,∠B=60°,∠C=90°.三角形为直角三角形;
故选:B.
6.解:①若4是腰,则另一腰也是4,底是8,但是4+4=8,故不构成三角形,舍去.
②若4是底,则腰是8,8.
4+8>8,符合条件.成立.
故周长为:4+8+8=20.
故选:B.
7.解:设此多边形为n边形,
根据题意得:180(n﹣2)=540,
解得:n=5,
∴这个正多边形的每一个外角等于:=72°.
故选:C.
8.解:A、甲和已知图形不符合全等三角形的判定定理,即不能推出甲图和已知△ABC全等′,故本选项错误;
B、乙和已知图形符合全等三角形的判定定理SAS,即能推出乙图和已知△ABC全等′,
丙图和已知图形符合全等三角形的判定定理AAS,即能推出丙图和已知△ABC全等,故本选项正确;
C、根据B选项得出此选项错误;
D、根据B选项得出此选项错误;
故选:B.
9.解:∵∠ACD是△ABC的外角,
∴∠ACD=∠B+∠A,
∴∠A=∠ACD﹣∠B,
∵∠ACD=110°,∠B=50°,
∴∠A=60°,
故选:D.
10.解:∵AB∥EF,
∴∠A=∠E,
在△ABC和△EFD中,
,
∴△ABC≌△EFD(ASA),
∴AC=ED=8,
∴AD=AE﹣ED=12﹣8=4,
∴CD=AC﹣AD=8﹣4=4.
故选:B.
11.解:多边形一条边上的一点(不是顶点)出发,连接各个顶点得到2003个三角形,
则这个多边形的边数为2013+1=2014.
故选:C.
12.解:∵AD是△ABC的中线,
∴BD=CD,
在△BDF和△CDE中,
,
∴△BDF≌△CDE(SAS),故④正确
∴CE=BF,∠F=∠CED,故①正确,
∴BF∥CE,故③正确,
∵BD=CD,点A到BD、CD的距离相等,
∴△ABD和△ACD面积相等,故②正确,
综上所述,正确的有4个,
故选:D.
二、填空题(每题4分,共24分)
13.解:生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有稳定性.
故答案为:稳定.
14.解:由题意得:5﹣3<x<5+3,
即:2<x<8,
故答案为:2<x<8.
15.解:∵∠A=40°,
∴∠B+∠C=180°﹣∠A=140°①,
∵∠B﹣∠C=40°②,
①+②得:2∠B=180°,
∴∠B=90°,
①﹣②得:2∠C=100°,
∴∠C=50°,
故答案为:90°;50°.
16.解:如图,在△ABC中,AB=AC;BD为腰AC上的中线;
设AB=λ,BC=μ;由题意得:
,
分别解这两个方程组得:或,
故它的底边长是7或11.
故答案为:7或11.
17.解:∠ABE=∠ABC﹣∠DBC=45°,
∴∠CEB=∠A+∠DBA=105°,
故答案为:105.
18.解:∵BE、CF都是△ABC的角平分线,
∴∠A=180°﹣(∠ABC+∠ACB)
=180°﹣2(∠DBC+∠BCD),
∵∠BDC=180°﹣(∠DBC+∠BCD),
∴∠A=180°﹣2(180°﹣∠BDC),
∴∠BDC=90°+∠A,
∵∠A=60°,
∴∠BDC=90°+×60°=90°+30°=120°,
故答案为:120°.
三、解答题(共60分)
19.解:(1)设边数为n,
则(n﹣2) 180°=2520﹣360,
解得:n=14.
所以这个多边形的边数是14.
(2)(n﹣2)×180°=144°n,
180°n﹣360°=144°n,
180°n﹣144°n=360°,
36°n=360°,
n=10.
答:n的值为10.
20.解:(1)∵腰长为6,
∴底边=16﹣2×6=4;
(2)当腰长为6,
∴底边=16﹣2×6=4,
∵6﹣4<6<6+4,
∴另两边为4和6,
当底边为6,
∴腰长==5,
∵5﹣5<6<5+5,
∴另两边为5和5.
21.解:∵∠ABC=66°,∠ACB=54°,
∴∠A=180°﹣∠ABC﹣∠ACB=180°﹣66°﹣54°=60°.
又∵BE是AC边上的高,所以∠AEB=90°,
∴∠ABE=180°﹣∠BAC﹣∠AEB=180°﹣90°﹣60°=30°.
同理,∠ACF=30°,
∴∠BHC=∠BEC+∠ACF=90°+30°=120°.
22.解:∵△ABF≌△DEC,
∴AB=DE,BF=CE,∠B=∠E,
又∵BC=BF+CF,EF=CE+CF,
∴BC=EF,
在△ABC与△DEF中,
,
∴△ABC≌△DEF(SAS),
故答案为:DE;CE;∠E;FC;FC;EF;AB=DE;∠B=∠E;BC=EF;SAS.
23.解:(1)BD=DC(或点D是线段BC的中点)或FD=ED或CF=BE中
任选一个即可.
(2)以BD=DC为例进行证明:
∵CF∥BE,
∴∠FCD=∠EBD,
在△BDE与△CDF中,
∵,
∴△BDE≌△CDF(ASA)
24.证明:∵AD是△ABC的高,
∴∠ADB=∠ADC=90°.
在Rt△BFD和Rt△ACD中
,
∴Rt△BFD≌Rt△ACD(HL).
25.证明:(1)∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(2)∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE.
一、选择题(每题3分,共36分)
1.下列每组数分别表示三根木棒的长度,将它们首尾连接后,能摆成三角形的一组是( )
A.1,2,6 B.2,2,4 C.1,2,3 D.2,3,4
2.图中能表示△ABC的BC边上的高的是( )
A. B.
C. D.
3.能将三角形的面积平分的是三角形的( )
A.三条中线 B.三条高
C.三条角平分线 D.三边的垂直平分线
4.下列说法正确的是( )
A.形状相同的两个三角形全等 B.面积相等的两个三角形全等
C.完全重合的两个三角形全等 D.所有的等边三角形全等
5.在下列条件中:①∠A+∠B=∠C;②∠A=∠B=2∠C;③∠A:∠B:∠C=1:2:3,能确定△ABC为直角三角形的条件有( )
A.1个 B.2个 C.3个 D.0个
6.一等腰三角形的两边长分别为4和8,则这个等腰三角形的周长为( )
A.16 B.20 C.18 D.16或20
7.一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )
A.108° B.90° C.72° D.60°
8.已知△ABC的六个元素如图,则甲、乙、丙三个三角形中和△ABC全等的图形是( )
A.甲、乙 B.乙、丙 C.只有乙 D.只有丙
9.如图,∠ACD是△ABC的外角,若∠ACD=110°,∠B=50°,则∠A=( )
A.40° B.50° C.55° D.60°
10.如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=12,AC=8,则CD的长为( )
A.5.5 B.4 C.4.5 D.3
11.从多边形一条边上的一点(不是顶点)出发,连接各个顶点得到2013个三角形,则这个多边形的边数为( )
A.2011 B.2015 C.2014 D.2016
12.如图,AD是△ABC的中线,E、F分别是AD和AD延长线上的点,且DE=DF,连接BF、CE,下列说法:①CE=BF;②△ABD和△ACD的面积相等;③BF∥CE;④△BDF≌△CDE,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每题4分,共24分)
13.生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有 性.
14.如果三角形的两边长分别是3和5,那么它的第三边x的取值范围是 .
15.已知在△ABC中,∠A=40°,∠B﹣∠C=40°,则∠B= ,∠C= .
16.等腰三角形一腰上的中线将其周长分为15和12两部分,则它的底边长是 .
17.如图是一副三角尺拼成的图案,则∠CEB= °.
18.如图,BE,CF都是△ABC的角平分线,且∠A=60°,则∠BDC= .
三、解答题(共60分)
19.(1)一个多边形的内角和与外交和相加后的结果是2520度,试求这个多边形的边数.
(2)一个正n边形的每个内角的度数为144度,求n的值.
20.已知等腰三角形的周长为16,
(1)若腰长为6,求它的底边长.
(2)若一边长为6,求它的另外两边的长.
21.在△ABC中,已知∠ABC=66°,∠ACB=54°,BE是AC上的高,CF是AB上的高,H是BE和CF的交点,求∠ABE、∠ACF和∠BHC的度数.
22.如图,已知△ABF≌△DEC,且AC=DF,说明△ABC≌△DEF的理由.
解:∵△ABF≌△DEC
∴AB= ,BF= ,∠B= .
又∵BC=BF+ ,EF=CE+ .
∴BC= .
在△ABC与△DEF中,
,
,
,
∴△ABC≌△DEF( )
23.如图,在△ABC中,D是BC边上的点(不与B,C重合),F,E分别是AD及其延长线上的点,CF∥BE.请你添加一个条件,使△BDE≌△CDF(不再添加其它线段,不再标注或使用其他字母),并给出证明.
(1)你添加的条件是: ;
(2)证明:
24.已知:如图AD为△ABC的高,E为AC上一点BE交AD于F且有BF=AC,FD=CD.
求证:Rt△BFD≌Rt△ACD.
25.(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D和点E,证明:△ABD≌△ACE,DE=BD+CE;
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=a,其中a为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
参考答案
一、选择题(每题3分,共36分)
1.解:A、1+2<6,不能组成三角形,故此选项错误;
B、2+2=4,不能组成三角形,故此选项错误;
C、1+2=3,不能组成三角形,故此选项错误;
D、2+3>4,能组成三角形,故此选项正确;
故选:D.
2.解:题中需要画△ABC的BC边上的高.应当过顶点A向BC边作垂线,顶点A到垂足E的垂线段就为BC边上的高.钝角三角形钝角两夹边的高在三角形的外部.
故选:D.
3.解:三角形的中线将三角形分成面积相等的两部分.
故选:A.
4.解:A、形状相同的两个三角形全等,说法错误,应该是形状相同且大小也相同的两个三角形全等;
B、面积相等的两个三角形全等,说法错误;
C、完全重合的两个三角形全等,说法正确;
D、所有的等边三角形全等,说法错误;
故选:C.
5.解:∵∠A+∠B+∠C=180°,
∴若 ①∠A+∠B=∠C,则∠C=90°.三角形为直角三角形;
②∠A=∠B=2∠C,则∠A=∠B=72°,∠C=36°.三角形不是直角三角形;
③∠A:∠B:∠C=1:2:3,则∠A=30°,∠B=60°,∠C=90°.三角形为直角三角形;
故选:B.
6.解:①若4是腰,则另一腰也是4,底是8,但是4+4=8,故不构成三角形,舍去.
②若4是底,则腰是8,8.
4+8>8,符合条件.成立.
故周长为:4+8+8=20.
故选:B.
7.解:设此多边形为n边形,
根据题意得:180(n﹣2)=540,
解得:n=5,
∴这个正多边形的每一个外角等于:=72°.
故选:C.
8.解:A、甲和已知图形不符合全等三角形的判定定理,即不能推出甲图和已知△ABC全等′,故本选项错误;
B、乙和已知图形符合全等三角形的判定定理SAS,即能推出乙图和已知△ABC全等′,
丙图和已知图形符合全等三角形的判定定理AAS,即能推出丙图和已知△ABC全等,故本选项正确;
C、根据B选项得出此选项错误;
D、根据B选项得出此选项错误;
故选:B.
9.解:∵∠ACD是△ABC的外角,
∴∠ACD=∠B+∠A,
∴∠A=∠ACD﹣∠B,
∵∠ACD=110°,∠B=50°,
∴∠A=60°,
故选:D.
10.解:∵AB∥EF,
∴∠A=∠E,
在△ABC和△EFD中,
,
∴△ABC≌△EFD(ASA),
∴AC=ED=8,
∴AD=AE﹣ED=12﹣8=4,
∴CD=AC﹣AD=8﹣4=4.
故选:B.
11.解:多边形一条边上的一点(不是顶点)出发,连接各个顶点得到2003个三角形,
则这个多边形的边数为2013+1=2014.
故选:C.
12.解:∵AD是△ABC的中线,
∴BD=CD,
在△BDF和△CDE中,
,
∴△BDF≌△CDE(SAS),故④正确
∴CE=BF,∠F=∠CED,故①正确,
∴BF∥CE,故③正确,
∵BD=CD,点A到BD、CD的距离相等,
∴△ABD和△ACD面积相等,故②正确,
综上所述,正确的有4个,
故选:D.
二、填空题(每题4分,共24分)
13.解:生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有稳定性.
故答案为:稳定.
14.解:由题意得:5﹣3<x<5+3,
即:2<x<8,
故答案为:2<x<8.
15.解:∵∠A=40°,
∴∠B+∠C=180°﹣∠A=140°①,
∵∠B﹣∠C=40°②,
①+②得:2∠B=180°,
∴∠B=90°,
①﹣②得:2∠C=100°,
∴∠C=50°,
故答案为:90°;50°.
16.解:如图,在△ABC中,AB=AC;BD为腰AC上的中线;
设AB=λ,BC=μ;由题意得:
,
分别解这两个方程组得:或,
故它的底边长是7或11.
故答案为:7或11.
17.解:∠ABE=∠ABC﹣∠DBC=45°,
∴∠CEB=∠A+∠DBA=105°,
故答案为:105.
18.解:∵BE、CF都是△ABC的角平分线,
∴∠A=180°﹣(∠ABC+∠ACB)
=180°﹣2(∠DBC+∠BCD),
∵∠BDC=180°﹣(∠DBC+∠BCD),
∴∠A=180°﹣2(180°﹣∠BDC),
∴∠BDC=90°+∠A,
∵∠A=60°,
∴∠BDC=90°+×60°=90°+30°=120°,
故答案为:120°.
三、解答题(共60分)
19.解:(1)设边数为n,
则(n﹣2) 180°=2520﹣360,
解得:n=14.
所以这个多边形的边数是14.
(2)(n﹣2)×180°=144°n,
180°n﹣360°=144°n,
180°n﹣144°n=360°,
36°n=360°,
n=10.
答:n的值为10.
20.解:(1)∵腰长为6,
∴底边=16﹣2×6=4;
(2)当腰长为6,
∴底边=16﹣2×6=4,
∵6﹣4<6<6+4,
∴另两边为4和6,
当底边为6,
∴腰长==5,
∵5﹣5<6<5+5,
∴另两边为5和5.
21.解:∵∠ABC=66°,∠ACB=54°,
∴∠A=180°﹣∠ABC﹣∠ACB=180°﹣66°﹣54°=60°.
又∵BE是AC边上的高,所以∠AEB=90°,
∴∠ABE=180°﹣∠BAC﹣∠AEB=180°﹣90°﹣60°=30°.
同理,∠ACF=30°,
∴∠BHC=∠BEC+∠ACF=90°+30°=120°.
22.解:∵△ABF≌△DEC,
∴AB=DE,BF=CE,∠B=∠E,
又∵BC=BF+CF,EF=CE+CF,
∴BC=EF,
在△ABC与△DEF中,
,
∴△ABC≌△DEF(SAS),
故答案为:DE;CE;∠E;FC;FC;EF;AB=DE;∠B=∠E;BC=EF;SAS.
23.解:(1)BD=DC(或点D是线段BC的中点)或FD=ED或CF=BE中
任选一个即可.
(2)以BD=DC为例进行证明:
∵CF∥BE,
∴∠FCD=∠EBD,
在△BDE与△CDF中,
∵,
∴△BDE≌△CDF(ASA)
24.证明:∵AD是△ABC的高,
∴∠ADB=∠ADC=90°.
在Rt△BFD和Rt△ACD中
,
∴Rt△BFD≌Rt△ACD(HL).
25.证明:(1)∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(2)∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE.
