2022-2023学年鲁教版(五四学制)九年级数学上册第2章直角三角形的边角关系 同步达标测试题(含解析)
文档属性
| 名称 | 2022-2023学年鲁教版(五四学制)九年级数学上册第2章直角三角形的边角关系 同步达标测试题(含解析) | 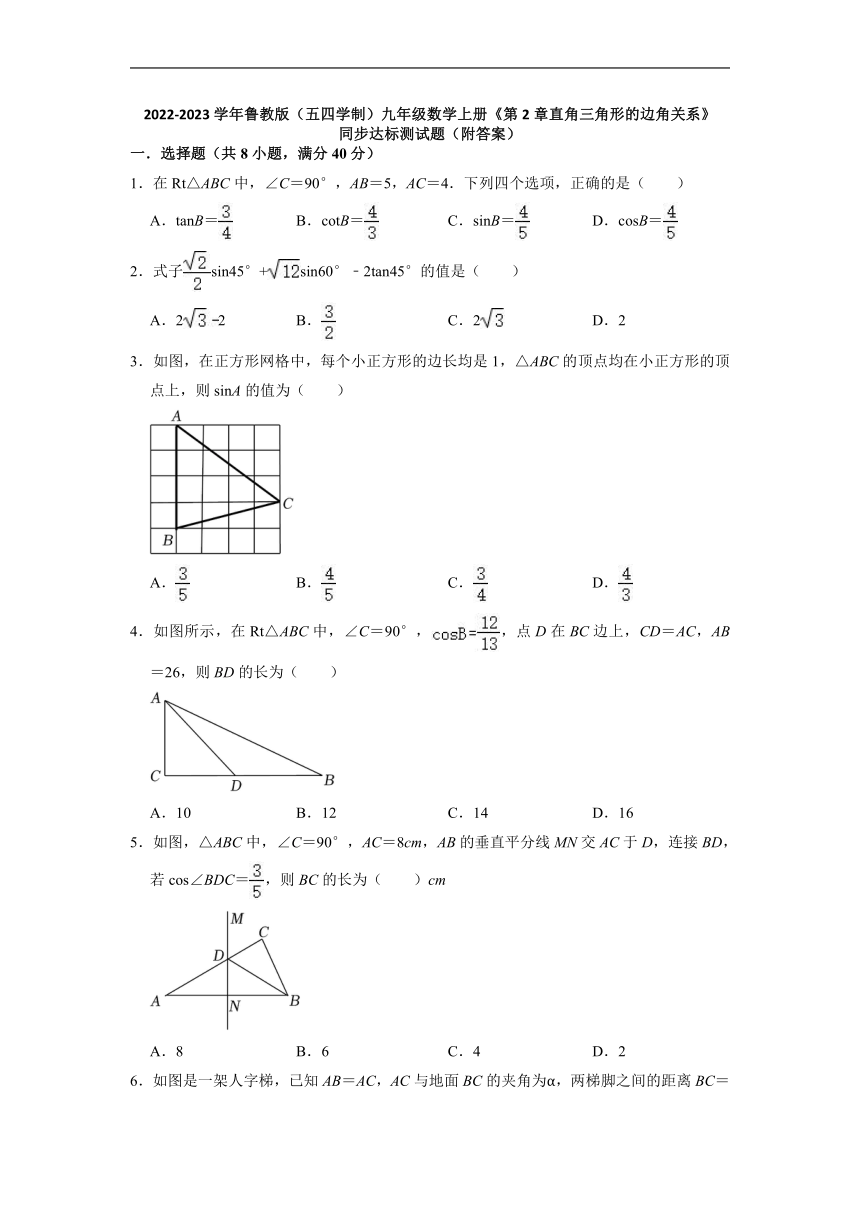 | |
| 格式 | docx | ||
| 文件大小 | 424.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 11:06:43 | ||
图片预览




文档简介
2022-2023学年鲁教版(五四学制)九年级数学上册《第2章直角三角形的边角关系》
同步达标测试题(附答案)
一.选择题(共8小题,满分40分)
1.在Rt△ABC中,∠C=90°,AB=5,AC=4.下列四个选项,正确的是( )
A.tanB= B.cotB= C.sinB= D.cosB=
2.式子sin45°+sin60°﹣2tan45°的值是( )
A.22 B. C.2 D.2
3.如图,在正方形网格中,每个小正方形的边长均是1,△ABC的顶点均在小正方形的顶点上,则sinA的值为( )
A. B. C. D.
4.如图所示,在Rt△ABC中,∠C=90°,,点D在BC边上,CD=AC,AB=26,则BD的长为( )
A.10 B.12 C.14 D.16
5.如图,△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于D,连接BD,若cos∠BDC=,则BC的长为( )cm
A.8 B.6 C.4 D.2
6.如图是一架人字梯,已知AB=AC,AC与地面BC的夹角为α,两梯脚之间的距离BC=8米,则线段AB长为( )米.
A.4cosα B.4sinα C.4tanα D.
7.如图,一辆小车沿着坡度为i=1:的斜坡向上行驶了100米,则此时该小车上升的高度为( )
A.50米 B.50米 C.50米 D.100米
8.如图,校内数学兴趣小组组织了一次测量探究活动.大楼的顶部竖有一块广告牌CD,小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:,AB=12米,AE=24米.测角器的高度忽略不计,则广告牌CD的高度约为( )(结果精确到0.1米,参考数据:≈1.41,≈1.73,sin53°≈,cos53°≈,tan53°≈)
A.2.4米 B.4.2米 C.8.4米 D.8.6米
二.填空题(共8小题,满分40分)
9.在Rt△ABC中,∠B=90°,AC=200,sinA=0.6,则BC= .
10.在锐角△ABC中,若,则∠C的度数是 度.
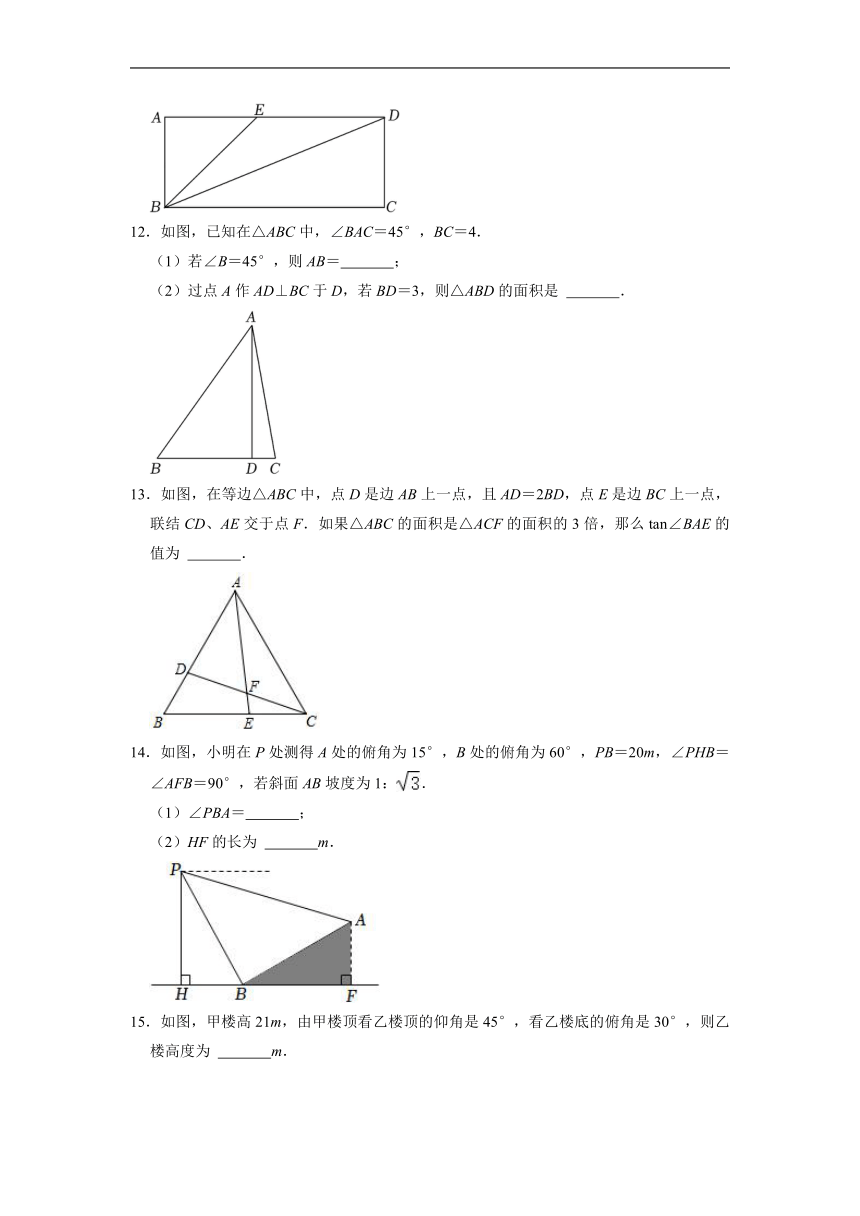
11.如图,在矩形ABCD中,E为AD上的点,AE=AB,BE=DE,则tan∠BDE= .
12.如图,已知在△ABC中,∠BAC=45°,BC=4.
(1)若∠B=45°,则AB= ;
(2)过点A作AD⊥BC于D,若BD=3,则△ABD的面积是 .
13.如图,在等边△ABC中,点D是边AB上一点,且AD=2BD,点E是边BC上一点,联结CD、AE交于点F.如果△ABC的面积是△ACF的面积的3倍,那么tan∠BAE的值为 .
14.如图,小明在P处测得A处的俯角为15°,B处的俯角为60°,PB=20m,∠PHB=∠AFB=90°,若斜面AB坡度为1:.
(1)∠PBA= ;
(2)HF的长为 m.
15.如图,甲楼高21m,由甲楼顶看乙楼顶的仰角是45°,看乙楼底的俯角是30°,则乙楼高度为 m.
16.一大门的栏杆如图所示,杆BA垂直于地面AE于A,杆CD平行于地面AE,已知AB=1米,BC=2.4米,∠BCD=150°,则此时杆CD到地面AE的距离是 米.
三.解答题(共6小题,满分40分)
17.计算:.
18.如图,在Rt△ABC中,∠C=90°,AB=10,tan∠A=,求BC的长和sin∠B的值.
19.如图,在△ABC中,BA=BC,点E在BC上,且AE⊥BC,cos∠B=,EC=3.
(1)分别求AB和AE;
(2)若点P在AB边上,且BP=4,求△BPE的面积.
20.位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道MP上架设测角仪,先在点M处测得观星台最高点A的仰角为22°,然后沿MP方向前进16m到达点N处,测得点A的仰角为45°,测角仪的高度为1.6m.
(Ⅰ)求观星台最高点A距离地面的高度(结果精确到0.1m);
(Ⅱ)“景点简介”显示,观星台的高度为12.6m,请计算本次测量结果的误差.
参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,≈1.41.
21.如图,某数学活动小组进行综合实践活动测量学校旗杆AB的高度,从旗杆正前方2米处的点C出发,沿斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,仪器的高DE为1.5米.已知A,B,C,D,E,M在同一平面内,∠DCM=30°,AB⊥BC,AB∥DE.求旗杆AB的高度.(参考数据:sin37°≈,cos37°≈,tan37°≈,计算结果保留根号)
22.如图,宝塔底座BC的高度为m,小明在D处测得底座最高点C的仰角为α,沿着DB方向前进n到达测量点E处,测得宝塔顶端A的仰角为β,求宝塔AB的高度.(用含α,β,m,n的式子表示)
参考答案
一.选择题(共8小题,满分40分)
1.解:如图,根据勾股定理得:BC===3,
tanB==,
cotB==,
sinB==,
cosB==,
故选:C.
2.解:原式=×+2×﹣2×1
=+3﹣2
=,
故选:B.
3.解:如图,过点C作CD⊥AB,垂足为D,
在Rt△ADC中,根据勾股定理得,AC===5,
∴sinA==.
故选:B.
4.解:在Rt△ABC中,∠C=90°,,AB=26,
∴BC=ABcosB=26×=24,
∴AC===10,
∵CD=AC,
∴CD=10,
∴BD=BC﹣CD=24﹣10=14,
故选:C.
5.解:在Rt△BCD中,
∵cos∠BDC==,
设CD=3k,BD=5k,
∴BC==4k.
∵MN是线段AB的垂直平分线,
∴AD=BD=5k.
∵AD+CD=8k=8cm,
∴k=1cm.
∴BC=4k=4cm.
故选:C.
6.解:过点A作AD⊥BC于点D,
∵AB=AC,BC=8米,
∴CD=BC=4米,
在Rt△ADC中,cosα=,
∴AC=,
∴AB=AC=.
故选:D.
7.解:设此时该小车上升的高度为x米,则水平前进了x米.
根据勾股定理可得:x2+(x)2=1002,
解得x=50.
即此时该小车上升的高度为50米.
故选:A.
8.解:过点B作BF⊥AE,垂足为F,过点B作BG⊥CE,垂足为G,
则BF=GE,BG=EF,
∵山坡AB的坡度i=1:,
∴==,
∴∠BAF=30°,
在Rt△ABF中,AB=12m,
∴BF=AB=6(m),
AF=BF=6(m),
∵AE=24m,
∴BG=EF=AF+AE=(6+24)米,
在Rt△BCG中,∠CBG=45°,
∴CG=BG tan45°=(6+24)米,
∴CE=CG+GE=(30+6)米,
在Rt△ADE中,∠DAE=53°,
∴DE=AE tan53°≈24×=32(米),
∴CD=CE﹣DE=30+6﹣32=6﹣2≈8.4(米),
故选:C.
二.填空题(共8小题,满分40分)
9.解:∵cos80°=sin10°,10°<20°<55°,
∴cos80°<sin20°<sin55°<1,
∵tan70°>tan45°=1,
∴cos80°<sin20°<sin55°<tan70°,
故答案为:cos80°<sin20°<sin55°<tan70°.
10.解:如图:
∵∠C=90°,BC=8,tanA==,
∴AC=6,
∵AB2=AC2+BC2,
∴AB2=62+82=100,
∴AB=10.
故答案为:10.
11.解:∵|sinα﹣|+(tanβ﹣1)2=0,
∴sinα﹣=0,tanβ﹣1=0,
∴sinα=,tanβ=1,
∴α=30°,β=45°,
则α+β=30°+45°=75°.
故答案为:75°.
12.解:在△ABC中,∠C=90°,tanA=,
∴∠A=30°,
∴∠ABC=90°﹣∠A=60°,
∵BD平分∠ABC,
∴∠DBC=∠ABC=30°,
在Rt△BDC中,CD=,
∴tan30°=,
∴BC===3,
∴AB=2BC=6,
∴AB的长为6,
故答案为:6.
13.解:如图,作AE⊥CD,交CD延长线于E,作BF⊥AE于F,则四边形BCEF是矩形.
在Rt△BCD中,∵∠C=90°,BD=40,∠BDC=65°,
∴BC=BD sin∠BDC≈40×0.91=36.4,∠CBD=90°﹣∠BDC=25°,
∴FE=BC≈36.4.
∵∠CBF=∠ABD=90°,
∴∠ABF=∠CBD=25°,
∴∠BAF=90°﹣∠ABF=65°.
在Rt△ABF中,∵∠AFB=90°,AB=30,∠BAF=65°,
∴AF=AB cos∠BAF≈30×0.42=12.6,
∴AE=AF+FE≈12.6+36.4=49.0.
即点A到CD的距离约为49.0.
故答案为:49.0.
14.解:过点B作BD⊥AC于点D,过点C作CE⊥AB于点E,则BD=AD=3,CD=1,如图所示.
AB==3,BC==.
∵AC BD=AB CE,即×2×3=×3 CE,
∴CE=,
∴sin∠ABC===.
故答案为:.
15.解:过点A作AE⊥BC交BC的延长线于点E,
由题意得:BC=12海里,∠ABC=90°﹣60°=30°,∠ACE=90°﹣30°=60°,
∴∠BAC=∠ACE﹣∠ABC=30°,
∴∠BAC=∠ABC,
∴AC=BC=12海里,
在Rt△ACE中,sin∠ACE=,
∴AE=AC sin∠ACE=12×=6(海里),
即小岛A到航线BC的距离是6海里,
故答案为:6.
16.解:过点D作DE⊥AB于点E,过点C作CF⊥DE于点F,
则四边形BCFE是矩形,
由题意得,AB=80米,DE=20米,∠ADE=90°﹣30°=60°,∠CDF=90°﹣45°=45°.
在Rt△ADE中,∠AED=90°,
∵tanADE==tan60°=,
∴AE=DE=60(米),
∴BE=AB﹣AE=80﹣60=20(米),
∵四边形BCFE是矩形,
∴CF=BE=20米,
在Rt△DCF中,∠DFC=90°,∠CDF=∠DCF=45°,
∴DF=CF=20米,
∴BC=EF=DE﹣DF=20﹣20≈14(米).
答:教学楼BC高约14米.
三.解答题(共6小题,满分40分)
17.解:
=
=
=.
18.解:∵tan∠A==,
∴AC=2BC,
在Rt△ABC中,AC2+BC2=AB2,
即(2BC)2+BC2=102,
解得BC=2,
∴AC=2BC=4,
sin∠B===.
19.解:(1)∵AE⊥BC,cos∠B=,
∴设AB=5x,BE=4x,
∵BA=BC,
∴BC=5x,
∵EC=3,CE=BC﹣BE,
∴5x﹣4x=3,
解得x=3,
∴AB=5×3=15,
BE=4×3=12,
在Rt△ABE中,根据勾股定理得,AE===9;
(2)△ABE的面积=BE AE=×12×9=54,
∵BP=4,
∴△BPE的面积=×54=14.4.
20.解:(1)过点A作AE⊥MP,交MP的延长线于点E,连接BC并延长,交AE于点D.
则CD⊥AE,BM=CN=DE=1.6m,BC=MN=16m,∠ABC=22°,∠ACD=45°,
设AD=xm,则CD=xm,BD=(16+x)m,
在Rt△ABD中,
tan22°=≈0.40,
∴x≈10.7m,
∴AE=AD+DE=10.7+1.6=12.3(m).
即观星台最高点A距离地面的高度约为12.3m.
(2)12.6﹣12.3=0.3(m).
∴本次测量结果的误差为0.3m.
21.解:过点E作EF⊥AB于点F,延长ED交BC于点G,
在Rt△CDG中,∠DCG=30°,
∴GD=CD=2(米),CG=CD cos∠DCG=2(米),
∴BG=CB+CG==2+2=4(米),
在Rt△AFE中,AF=EF tan∠AEF=4×=3(米),
∴AB=AF+BF=AF+ED+DG=3+1.5+2=(3+3.5)米,
答:旗杆AB的高度为(3+3.5)m.
22.解:在Rt△BCD中,∠CDB=α,BC=m,
tanα=,
∴BD=,
∴BE=BD﹣DE=﹣n,
在Rt△AEB中,∠AEB=β,
tanβ=,
∴AB=tanβ (﹣n)=.
答:宝塔AB的高度为.
同步达标测试题(附答案)
一.选择题(共8小题,满分40分)
1.在Rt△ABC中,∠C=90°,AB=5,AC=4.下列四个选项,正确的是( )
A.tanB= B.cotB= C.sinB= D.cosB=
2.式子sin45°+sin60°﹣2tan45°的值是( )
A.22 B. C.2 D.2
3.如图,在正方形网格中,每个小正方形的边长均是1,△ABC的顶点均在小正方形的顶点上,则sinA的值为( )
A. B. C. D.
4.如图所示,在Rt△ABC中,∠C=90°,,点D在BC边上,CD=AC,AB=26,则BD的长为( )
A.10 B.12 C.14 D.16
5.如图,△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于D,连接BD,若cos∠BDC=,则BC的长为( )cm
A.8 B.6 C.4 D.2
6.如图是一架人字梯,已知AB=AC,AC与地面BC的夹角为α,两梯脚之间的距离BC=8米,则线段AB长为( )米.
A.4cosα B.4sinα C.4tanα D.
7.如图,一辆小车沿着坡度为i=1:的斜坡向上行驶了100米,则此时该小车上升的高度为( )
A.50米 B.50米 C.50米 D.100米
8.如图,校内数学兴趣小组组织了一次测量探究活动.大楼的顶部竖有一块广告牌CD,小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:,AB=12米,AE=24米.测角器的高度忽略不计,则广告牌CD的高度约为( )(结果精确到0.1米,参考数据:≈1.41,≈1.73,sin53°≈,cos53°≈,tan53°≈)
A.2.4米 B.4.2米 C.8.4米 D.8.6米
二.填空题(共8小题,满分40分)
9.在Rt△ABC中,∠B=90°,AC=200,sinA=0.6,则BC= .
10.在锐角△ABC中,若,则∠C的度数是 度.
11.如图,在矩形ABCD中,E为AD上的点,AE=AB,BE=DE,则tan∠BDE= .
12.如图,已知在△ABC中,∠BAC=45°,BC=4.
(1)若∠B=45°,则AB= ;
(2)过点A作AD⊥BC于D,若BD=3,则△ABD的面积是 .
13.如图,在等边△ABC中,点D是边AB上一点,且AD=2BD,点E是边BC上一点,联结CD、AE交于点F.如果△ABC的面积是△ACF的面积的3倍,那么tan∠BAE的值为 .
14.如图,小明在P处测得A处的俯角为15°,B处的俯角为60°,PB=20m,∠PHB=∠AFB=90°,若斜面AB坡度为1:.
(1)∠PBA= ;
(2)HF的长为 m.
15.如图,甲楼高21m,由甲楼顶看乙楼顶的仰角是45°,看乙楼底的俯角是30°,则乙楼高度为 m.
16.一大门的栏杆如图所示,杆BA垂直于地面AE于A,杆CD平行于地面AE,已知AB=1米,BC=2.4米,∠BCD=150°,则此时杆CD到地面AE的距离是 米.
三.解答题(共6小题,满分40分)
17.计算:.
18.如图,在Rt△ABC中,∠C=90°,AB=10,tan∠A=,求BC的长和sin∠B的值.
19.如图,在△ABC中,BA=BC,点E在BC上,且AE⊥BC,cos∠B=,EC=3.
(1)分别求AB和AE;
(2)若点P在AB边上,且BP=4,求△BPE的面积.
20.位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道MP上架设测角仪,先在点M处测得观星台最高点A的仰角为22°,然后沿MP方向前进16m到达点N处,测得点A的仰角为45°,测角仪的高度为1.6m.
(Ⅰ)求观星台最高点A距离地面的高度(结果精确到0.1m);
(Ⅱ)“景点简介”显示,观星台的高度为12.6m,请计算本次测量结果的误差.
参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,≈1.41.
21.如图,某数学活动小组进行综合实践活动测量学校旗杆AB的高度,从旗杆正前方2米处的点C出发,沿斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,仪器的高DE为1.5米.已知A,B,C,D,E,M在同一平面内,∠DCM=30°,AB⊥BC,AB∥DE.求旗杆AB的高度.(参考数据:sin37°≈,cos37°≈,tan37°≈,计算结果保留根号)
22.如图,宝塔底座BC的高度为m,小明在D处测得底座最高点C的仰角为α,沿着DB方向前进n到达测量点E处,测得宝塔顶端A的仰角为β,求宝塔AB的高度.(用含α,β,m,n的式子表示)
参考答案
一.选择题(共8小题,满分40分)
1.解:如图,根据勾股定理得:BC===3,
tanB==,
cotB==,
sinB==,
cosB==,
故选:C.
2.解:原式=×+2×﹣2×1
=+3﹣2
=,
故选:B.
3.解:如图,过点C作CD⊥AB,垂足为D,
在Rt△ADC中,根据勾股定理得,AC===5,
∴sinA==.
故选:B.
4.解:在Rt△ABC中,∠C=90°,,AB=26,
∴BC=ABcosB=26×=24,
∴AC===10,
∵CD=AC,
∴CD=10,
∴BD=BC﹣CD=24﹣10=14,
故选:C.
5.解:在Rt△BCD中,
∵cos∠BDC==,
设CD=3k,BD=5k,
∴BC==4k.
∵MN是线段AB的垂直平分线,
∴AD=BD=5k.
∵AD+CD=8k=8cm,
∴k=1cm.
∴BC=4k=4cm.
故选:C.
6.解:过点A作AD⊥BC于点D,
∵AB=AC,BC=8米,
∴CD=BC=4米,
在Rt△ADC中,cosα=,
∴AC=,
∴AB=AC=.
故选:D.
7.解:设此时该小车上升的高度为x米,则水平前进了x米.
根据勾股定理可得:x2+(x)2=1002,
解得x=50.
即此时该小车上升的高度为50米.
故选:A.
8.解:过点B作BF⊥AE,垂足为F,过点B作BG⊥CE,垂足为G,
则BF=GE,BG=EF,
∵山坡AB的坡度i=1:,
∴==,
∴∠BAF=30°,
在Rt△ABF中,AB=12m,
∴BF=AB=6(m),
AF=BF=6(m),
∵AE=24m,
∴BG=EF=AF+AE=(6+24)米,
在Rt△BCG中,∠CBG=45°,
∴CG=BG tan45°=(6+24)米,
∴CE=CG+GE=(30+6)米,
在Rt△ADE中,∠DAE=53°,
∴DE=AE tan53°≈24×=32(米),
∴CD=CE﹣DE=30+6﹣32=6﹣2≈8.4(米),
故选:C.
二.填空题(共8小题,满分40分)
9.解:∵cos80°=sin10°,10°<20°<55°,
∴cos80°<sin20°<sin55°<1,
∵tan70°>tan45°=1,
∴cos80°<sin20°<sin55°<tan70°,
故答案为:cos80°<sin20°<sin55°<tan70°.
10.解:如图:
∵∠C=90°,BC=8,tanA==,
∴AC=6,
∵AB2=AC2+BC2,
∴AB2=62+82=100,
∴AB=10.
故答案为:10.
11.解:∵|sinα﹣|+(tanβ﹣1)2=0,
∴sinα﹣=0,tanβ﹣1=0,
∴sinα=,tanβ=1,
∴α=30°,β=45°,
则α+β=30°+45°=75°.
故答案为:75°.
12.解:在△ABC中,∠C=90°,tanA=,
∴∠A=30°,
∴∠ABC=90°﹣∠A=60°,
∵BD平分∠ABC,
∴∠DBC=∠ABC=30°,
在Rt△BDC中,CD=,
∴tan30°=,
∴BC===3,
∴AB=2BC=6,
∴AB的长为6,
故答案为:6.
13.解:如图,作AE⊥CD,交CD延长线于E,作BF⊥AE于F,则四边形BCEF是矩形.
在Rt△BCD中,∵∠C=90°,BD=40,∠BDC=65°,
∴BC=BD sin∠BDC≈40×0.91=36.4,∠CBD=90°﹣∠BDC=25°,
∴FE=BC≈36.4.
∵∠CBF=∠ABD=90°,
∴∠ABF=∠CBD=25°,
∴∠BAF=90°﹣∠ABF=65°.
在Rt△ABF中,∵∠AFB=90°,AB=30,∠BAF=65°,
∴AF=AB cos∠BAF≈30×0.42=12.6,
∴AE=AF+FE≈12.6+36.4=49.0.
即点A到CD的距离约为49.0.
故答案为:49.0.
14.解:过点B作BD⊥AC于点D,过点C作CE⊥AB于点E,则BD=AD=3,CD=1,如图所示.
AB==3,BC==.
∵AC BD=AB CE,即×2×3=×3 CE,
∴CE=,
∴sin∠ABC===.
故答案为:.
15.解:过点A作AE⊥BC交BC的延长线于点E,
由题意得:BC=12海里,∠ABC=90°﹣60°=30°,∠ACE=90°﹣30°=60°,
∴∠BAC=∠ACE﹣∠ABC=30°,
∴∠BAC=∠ABC,
∴AC=BC=12海里,
在Rt△ACE中,sin∠ACE=,
∴AE=AC sin∠ACE=12×=6(海里),
即小岛A到航线BC的距离是6海里,
故答案为:6.
16.解:过点D作DE⊥AB于点E,过点C作CF⊥DE于点F,
则四边形BCFE是矩形,
由题意得,AB=80米,DE=20米,∠ADE=90°﹣30°=60°,∠CDF=90°﹣45°=45°.
在Rt△ADE中,∠AED=90°,
∵tanADE==tan60°=,
∴AE=DE=60(米),
∴BE=AB﹣AE=80﹣60=20(米),
∵四边形BCFE是矩形,
∴CF=BE=20米,
在Rt△DCF中,∠DFC=90°,∠CDF=∠DCF=45°,
∴DF=CF=20米,
∴BC=EF=DE﹣DF=20﹣20≈14(米).
答:教学楼BC高约14米.
三.解答题(共6小题,满分40分)
17.解:
=
=
=.
18.解:∵tan∠A==,
∴AC=2BC,
在Rt△ABC中,AC2+BC2=AB2,
即(2BC)2+BC2=102,
解得BC=2,
∴AC=2BC=4,
sin∠B===.
19.解:(1)∵AE⊥BC,cos∠B=,
∴设AB=5x,BE=4x,
∵BA=BC,
∴BC=5x,
∵EC=3,CE=BC﹣BE,
∴5x﹣4x=3,
解得x=3,
∴AB=5×3=15,
BE=4×3=12,
在Rt△ABE中,根据勾股定理得,AE===9;
(2)△ABE的面积=BE AE=×12×9=54,
∵BP=4,
∴△BPE的面积=×54=14.4.
20.解:(1)过点A作AE⊥MP,交MP的延长线于点E,连接BC并延长,交AE于点D.
则CD⊥AE,BM=CN=DE=1.6m,BC=MN=16m,∠ABC=22°,∠ACD=45°,
设AD=xm,则CD=xm,BD=(16+x)m,
在Rt△ABD中,
tan22°=≈0.40,
∴x≈10.7m,
∴AE=AD+DE=10.7+1.6=12.3(m).
即观星台最高点A距离地面的高度约为12.3m.
(2)12.6﹣12.3=0.3(m).
∴本次测量结果的误差为0.3m.
21.解:过点E作EF⊥AB于点F,延长ED交BC于点G,
在Rt△CDG中,∠DCG=30°,
∴GD=CD=2(米),CG=CD cos∠DCG=2(米),
∴BG=CB+CG==2+2=4(米),
在Rt△AFE中,AF=EF tan∠AEF=4×=3(米),
∴AB=AF+BF=AF+ED+DG=3+1.5+2=(3+3.5)米,
答:旗杆AB的高度为(3+3.5)m.
22.解:在Rt△BCD中,∠CDB=α,BC=m,
tanα=,
∴BD=,
∴BE=BD﹣DE=﹣n,
在Rt△AEB中,∠AEB=β,
tanβ=,
∴AB=tanβ (﹣n)=.
答:宝塔AB的高度为.
