2022-2023学年北师大版数学七年级上册《2.11有理数的混合运算》解答题优生辅导训练(含答案)
文档属性
| 名称 | 2022-2023学年北师大版数学七年级上册《2.11有理数的混合运算》解答题优生辅导训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 115.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 00:00:00 | ||
图片预览


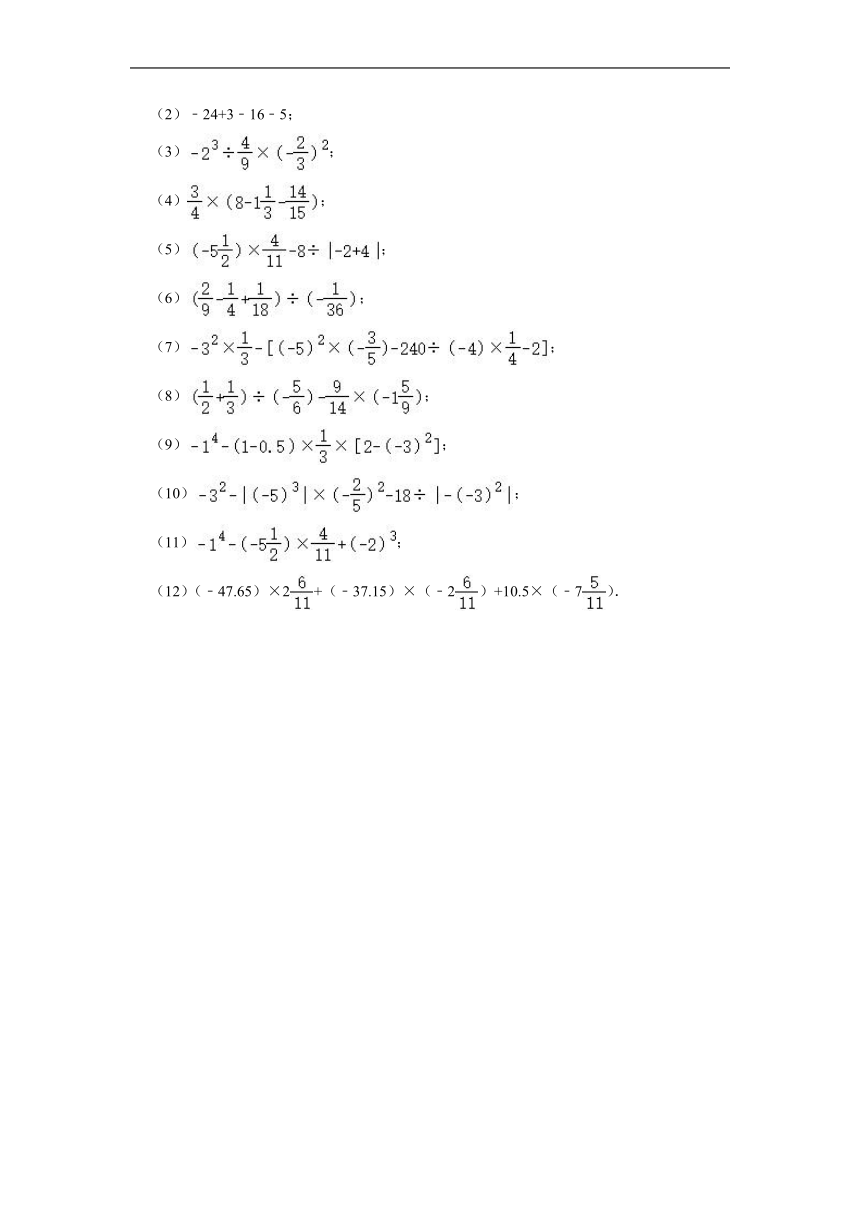

文档简介
2022-2023学年北师大版七年级数学上册《2.11有理数的混合运算》
解答题优生辅导训练(附答案)
1.已知x、y为有理数,现规定一种新运算※,满足x※y=xy+1.
(1)求2※4的值;
(2)求(1※4)※(﹣2)的值;
(3)任意选择两个有理数(至少有一个是负数),分别填入下列□和〇中,并比较它们的运算结果:□※〇和〇※□;
(4)探索a※(b+c)与a※b+a※c的关系,并用等式把它们表达出来.
2.计算:(﹣2)4÷(﹣2)2+5×(﹣)﹣0.25.
3.计算:.
4.计算:(﹣2)2+[18﹣(﹣3)×2]÷4.
5.有四个有理数3,4,﹣6,10,运用“二十四点”游戏规则,写出两种不同的方法的运算式,使其结果等于24.
6.计算:﹣42×+|﹣2|3×(﹣)3
7.计算:(﹣2)3+(﹣3)×[(﹣4)2+2]﹣(﹣3)2÷(﹣2)
8.计算:2×(﹣3)2.
9.计算:.
10.我们常用的数是十进制数,如4657=4×103+6×102+5×101+7×100,数要用10个数码(又叫数字):0,1,2,3,4,5,6,7,8,9,在电子计算机中用的二进制,只要两个数码:0和1,如二进制中110=1×22+1×21+0×20等于十进制的数6,110101=1×25+1×24+0×23+1×22+0×21+1×20等于十进制的数53.那么二进制中的数101011等于十进制中的哪个数?
11.如果a、b互为相反数,c、d互为倒数,x的绝对值是1,求的值.
12.已知a,b互为相反数,c,d互为倒数,x的绝对值为1,求a+b+x2﹣cdx.
13.计算题
(1)(﹣2)3+(﹣3)×[(﹣4)2+2]﹣(﹣3)2÷(﹣2);
(2).
14.我们把符号“n!”读作“n的阶乘”,规定“其中n为自然数,当n≠0时,n!=n (n﹣1) (n﹣2)…2 1,当n=0时,0!=1”.例如:6!=6×5×4×3×2×1=720.
又规定“在含有阶乘和加、减、乘、除运算时,应先计算阶乘,再乘除,后加减,有括号就先算括号里面的”.
按照以上的定义和运算顺序,计算:
(1)4!= ;
(2)= ;
(3)(3+2)!﹣4!= ;
(4)用具体数试验一下,看看等式(m+n)!=m!+n!是否成立?
15.已知a、b互为相反数且a≠0,c、d互为倒数,m的绝对值是最小的正整数,求的值.
16.已知a,b互为相反数,c,d互为倒数,x的绝对值等于2,求x2﹣(a+b+cd)+(a+b)2021+(﹣cd)2021的值.
17.计算:(﹣3)2÷2×(﹣)+4+22×(﹣).
18.计算:﹣22﹣÷(﹣2)3
19.若a,b互为相反数,c,d互为倒数,|m|=2,求+m2﹣3cd的值.
20.计算:﹣34+(﹣0.25)100×4100+()×()﹣2÷|﹣2|.
21.如果规定*的意思是a*b=,求2*(﹣3)*4的值.
22.25×﹣(﹣25)×+25×(﹣)
23.我们定义一种新运算:a*b=a2﹣b+ab.例如:1*3=12﹣3+1×3=1
(1)求2*(﹣3)的值.
(2)求(﹣2)*[2*(﹣3)]的值.
24..
25.计算:.
26.对于有理数a、b,定义一种新运算“⊙”,规定:a⊙b=|a+b|+|a﹣b|.
(1)计算2⊙(﹣4)的值;
(2)若a,b在数轴上的位置如图所示,化简a⊙b.
27.计算:(1);
(2)﹣24+3﹣16﹣5;
(3);
(4);
(5);
(6);
(7);
(8);
(9);
(10);
(11);
(12)(﹣47.65)×2+(﹣37.15)×(﹣2)+10.5×(﹣7).
参考答案
1.解:(1)2※4=2×4+1=9;
(2)(1※4)※(﹣2)=(1×4+1)×(﹣2)+1=﹣9;
(3)令□为﹣1,〇为5,(﹣1)※5=﹣1×5+1=﹣4,
5※(﹣1)=5×(﹣1)+1=﹣4;
(4)∵a※(b+c)=a(b+c)+1=ab+ac+1,a※b+a※c=ab+1+ac+1=ab+ac+2.
∴a※(b+c)+1=a※b+a※c.
2.解:原式=16÷+×(﹣)﹣=﹣﹣=.
3.解:原式=
=
=
=.
4.解:原式=4+24÷4=10.
5.解:答案不唯一.
(1)[10+(﹣6)+4]×3;
(2)(10﹣4)×3﹣(﹣6);
(3)4﹣[10×(﹣6)÷3];
(4)10﹣3×(﹣6)﹣4.
6.解:原式==﹣1﹣1=﹣2.
7.解:原式=﹣8+(﹣3)×18﹣9÷(﹣2),
=﹣8﹣54﹣9÷(﹣2),
=﹣62+4.5,
=﹣57.5.
8.解:2×(﹣3)2
=2×9﹣5×2×2
=18﹣20
=﹣2.
9.解:
=
=
=18.
10.解:101011=1×25+0×24+1×23+0×22+1×21+1×20=32+0+8+0+2+1=43.
11.解:∵a,b互为相反数,
∴a+b=0,
∵c,d互为倒数,
∴cd=1,
∵|x|=1,
∴x=±1,
∴原式=0+1+1=2或0﹣1+1=0.
12.解:∵a,b互为相反数,
∴a+b=0,
∵c,d互为倒数,
∴cd=1,
∵|x|=1,∴x=±1,
当x=1时,
a+b+x2﹣cdx=0+12﹣1×1=0;
当x=﹣1时,
a+b+x2+cdx=0+(﹣1)2﹣1×(﹣1)=2.
13.解:(1)(﹣2)3+(﹣3)×[(﹣4)2+2]﹣(﹣3)2÷(﹣2)
=﹣8+(﹣3)×18+
=﹣62+
=﹣;
(2)
=()×(﹣24)+1
=+1
=﹣3﹣32+66+1
=32.
14.解:(1)4!=4×3×2×1=24;
(2)=;
(3)(3+2)!﹣4!=5×4×3×2×1﹣4×3×2×1=120﹣24=96;
(4)如当m=3,n=2时,(m+n)!=(3+2)!=120,m!+n!=3!+2!=8.
但是当m=n=1时,(m+n)!=m!+n!
所以,当m、m不同时为1时,(m+n)!≠m!+n!,等式(m+n)!=m!+n!不成立.
15.解:根据题意可得a+b=0,cd=1,m=±1,
∴m2=1.
∴=1+1+0﹣1=1.
16.解:由题意可得:a+b=0,cd=1;|x|=2,即x2=4.
原式=4﹣1+0﹣1=2.
17.解:原式=﹣9××+4+4×(﹣)
=﹣+4+(﹣)
=﹣.
18.解:原式=﹣4﹣÷(﹣8)=﹣4+=﹣3.
19.解:由题意得:a+b=0,cd=1,m2=4,
原式=m2﹣3=4﹣3=1.
20.解:原式=﹣81+1+×36×=﹣81+1+3=﹣77.
21.解:∵2*(﹣3)==6,
∴2*(﹣3)*4=6*4==2.4.
22.解:原式=25×(+﹣)=25×1=25.
23.解:(1)2*(﹣3)=22﹣(﹣3)+2×(﹣3)=4+3﹣6=1;
(2)(﹣2)*[2*(﹣3)]=(﹣2)*1=(﹣2)2﹣1+(﹣2)×1=4﹣1﹣2=1.
24.解:
=﹣18÷9+5×(﹣)+3
=﹣2﹣+3
=.
25.解:原式=﹣+﹣+…+﹣=1﹣=.
26.解:(1)2⊙(﹣4)=|2﹣4|+|2+4|=2+6=8;
(2)由数轴知a<0<b,且|a|>|b|,
则a+b<0、a﹣b<0,
所以原式=﹣(a+b)﹣(a﹣b)
=﹣a﹣b﹣a+b
=﹣2a.
27.解:(1)原式=﹣+﹣=﹣=3﹣6=﹣3;
(2)原式=﹣21﹣16﹣5=﹣37﹣5=﹣42;
(3)原式=﹣8××=﹣8;
(4)原式=×8﹣×﹣×=6﹣1﹣=;
(5)原式=﹣×﹣8÷2=﹣2﹣4=﹣6;
(6)原式=×(﹣36)﹣×(﹣36)+×(﹣36)=﹣8+9﹣2=1﹣2=﹣1;
(7)原式=﹣9×﹣[25×(﹣)﹣240×(﹣)×﹣2]
=﹣3﹣(﹣15+15﹣2)=﹣3+2=﹣1;
(8)原式=×(﹣)﹣×(﹣)=﹣1+1=0;
(9)原式=﹣1﹣××(2﹣9)=﹣1﹣×(﹣7)=﹣1+=;
(10)原式=﹣9﹣125×﹣18÷9=﹣9﹣20﹣2=﹣31;
(11)原式=﹣1﹣(﹣)×﹣8=﹣1+2﹣8=﹣7;
(12)原式=(37.15﹣47.65)×2﹣10.5×7
=﹣10.5×﹣10.5×
=﹣10.5×(+)
=﹣10.5×10
=﹣105.
解答题优生辅导训练(附答案)
1.已知x、y为有理数,现规定一种新运算※,满足x※y=xy+1.
(1)求2※4的值;
(2)求(1※4)※(﹣2)的值;
(3)任意选择两个有理数(至少有一个是负数),分别填入下列□和〇中,并比较它们的运算结果:□※〇和〇※□;
(4)探索a※(b+c)与a※b+a※c的关系,并用等式把它们表达出来.
2.计算:(﹣2)4÷(﹣2)2+5×(﹣)﹣0.25.
3.计算:.
4.计算:(﹣2)2+[18﹣(﹣3)×2]÷4.
5.有四个有理数3,4,﹣6,10,运用“二十四点”游戏规则,写出两种不同的方法的运算式,使其结果等于24.
6.计算:﹣42×+|﹣2|3×(﹣)3
7.计算:(﹣2)3+(﹣3)×[(﹣4)2+2]﹣(﹣3)2÷(﹣2)
8.计算:2×(﹣3)2.
9.计算:.
10.我们常用的数是十进制数,如4657=4×103+6×102+5×101+7×100,数要用10个数码(又叫数字):0,1,2,3,4,5,6,7,8,9,在电子计算机中用的二进制,只要两个数码:0和1,如二进制中110=1×22+1×21+0×20等于十进制的数6,110101=1×25+1×24+0×23+1×22+0×21+1×20等于十进制的数53.那么二进制中的数101011等于十进制中的哪个数?
11.如果a、b互为相反数,c、d互为倒数,x的绝对值是1,求的值.
12.已知a,b互为相反数,c,d互为倒数,x的绝对值为1,求a+b+x2﹣cdx.
13.计算题
(1)(﹣2)3+(﹣3)×[(﹣4)2+2]﹣(﹣3)2÷(﹣2);
(2).
14.我们把符号“n!”读作“n的阶乘”,规定“其中n为自然数,当n≠0时,n!=n (n﹣1) (n﹣2)…2 1,当n=0时,0!=1”.例如:6!=6×5×4×3×2×1=720.
又规定“在含有阶乘和加、减、乘、除运算时,应先计算阶乘,再乘除,后加减,有括号就先算括号里面的”.
按照以上的定义和运算顺序,计算:
(1)4!= ;
(2)= ;
(3)(3+2)!﹣4!= ;
(4)用具体数试验一下,看看等式(m+n)!=m!+n!是否成立?
15.已知a、b互为相反数且a≠0,c、d互为倒数,m的绝对值是最小的正整数,求的值.
16.已知a,b互为相反数,c,d互为倒数,x的绝对值等于2,求x2﹣(a+b+cd)+(a+b)2021+(﹣cd)2021的值.
17.计算:(﹣3)2÷2×(﹣)+4+22×(﹣).
18.计算:﹣22﹣÷(﹣2)3
19.若a,b互为相反数,c,d互为倒数,|m|=2,求+m2﹣3cd的值.
20.计算:﹣34+(﹣0.25)100×4100+()×()﹣2÷|﹣2|.
21.如果规定*的意思是a*b=,求2*(﹣3)*4的值.
22.25×﹣(﹣25)×+25×(﹣)
23.我们定义一种新运算:a*b=a2﹣b+ab.例如:1*3=12﹣3+1×3=1
(1)求2*(﹣3)的值.
(2)求(﹣2)*[2*(﹣3)]的值.
24..
25.计算:.
26.对于有理数a、b,定义一种新运算“⊙”,规定:a⊙b=|a+b|+|a﹣b|.
(1)计算2⊙(﹣4)的值;
(2)若a,b在数轴上的位置如图所示,化简a⊙b.
27.计算:(1);
(2)﹣24+3﹣16﹣5;
(3);
(4);
(5);
(6);
(7);
(8);
(9);
(10);
(11);
(12)(﹣47.65)×2+(﹣37.15)×(﹣2)+10.5×(﹣7).
参考答案
1.解:(1)2※4=2×4+1=9;
(2)(1※4)※(﹣2)=(1×4+1)×(﹣2)+1=﹣9;
(3)令□为﹣1,〇为5,(﹣1)※5=﹣1×5+1=﹣4,
5※(﹣1)=5×(﹣1)+1=﹣4;
(4)∵a※(b+c)=a(b+c)+1=ab+ac+1,a※b+a※c=ab+1+ac+1=ab+ac+2.
∴a※(b+c)+1=a※b+a※c.
2.解:原式=16÷+×(﹣)﹣=﹣﹣=.
3.解:原式=
=
=
=.
4.解:原式=4+24÷4=10.
5.解:答案不唯一.
(1)[10+(﹣6)+4]×3;
(2)(10﹣4)×3﹣(﹣6);
(3)4﹣[10×(﹣6)÷3];
(4)10﹣3×(﹣6)﹣4.
6.解:原式==﹣1﹣1=﹣2.
7.解:原式=﹣8+(﹣3)×18﹣9÷(﹣2),
=﹣8﹣54﹣9÷(﹣2),
=﹣62+4.5,
=﹣57.5.
8.解:2×(﹣3)2
=2×9﹣5×2×2
=18﹣20
=﹣2.
9.解:
=
=
=18.
10.解:101011=1×25+0×24+1×23+0×22+1×21+1×20=32+0+8+0+2+1=43.
11.解:∵a,b互为相反数,
∴a+b=0,
∵c,d互为倒数,
∴cd=1,
∵|x|=1,
∴x=±1,
∴原式=0+1+1=2或0﹣1+1=0.
12.解:∵a,b互为相反数,
∴a+b=0,
∵c,d互为倒数,
∴cd=1,
∵|x|=1,∴x=±1,
当x=1时,
a+b+x2﹣cdx=0+12﹣1×1=0;
当x=﹣1时,
a+b+x2+cdx=0+(﹣1)2﹣1×(﹣1)=2.
13.解:(1)(﹣2)3+(﹣3)×[(﹣4)2+2]﹣(﹣3)2÷(﹣2)
=﹣8+(﹣3)×18+
=﹣62+
=﹣;
(2)
=()×(﹣24)+1
=+1
=﹣3﹣32+66+1
=32.
14.解:(1)4!=4×3×2×1=24;
(2)=;
(3)(3+2)!﹣4!=5×4×3×2×1﹣4×3×2×1=120﹣24=96;
(4)如当m=3,n=2时,(m+n)!=(3+2)!=120,m!+n!=3!+2!=8.
但是当m=n=1时,(m+n)!=m!+n!
所以,当m、m不同时为1时,(m+n)!≠m!+n!,等式(m+n)!=m!+n!不成立.
15.解:根据题意可得a+b=0,cd=1,m=±1,
∴m2=1.
∴=1+1+0﹣1=1.
16.解:由题意可得:a+b=0,cd=1;|x|=2,即x2=4.
原式=4﹣1+0﹣1=2.
17.解:原式=﹣9××+4+4×(﹣)
=﹣+4+(﹣)
=﹣.
18.解:原式=﹣4﹣÷(﹣8)=﹣4+=﹣3.
19.解:由题意得:a+b=0,cd=1,m2=4,
原式=m2﹣3=4﹣3=1.
20.解:原式=﹣81+1+×36×=﹣81+1+3=﹣77.
21.解:∵2*(﹣3)==6,
∴2*(﹣3)*4=6*4==2.4.
22.解:原式=25×(+﹣)=25×1=25.
23.解:(1)2*(﹣3)=22﹣(﹣3)+2×(﹣3)=4+3﹣6=1;
(2)(﹣2)*[2*(﹣3)]=(﹣2)*1=(﹣2)2﹣1+(﹣2)×1=4﹣1﹣2=1.
24.解:
=﹣18÷9+5×(﹣)+3
=﹣2﹣+3
=.
25.解:原式=﹣+﹣+…+﹣=1﹣=.
26.解:(1)2⊙(﹣4)=|2﹣4|+|2+4|=2+6=8;
(2)由数轴知a<0<b,且|a|>|b|,
则a+b<0、a﹣b<0,
所以原式=﹣(a+b)﹣(a﹣b)
=﹣a﹣b﹣a+b
=﹣2a.
27.解:(1)原式=﹣+﹣=﹣=3﹣6=﹣3;
(2)原式=﹣21﹣16﹣5=﹣37﹣5=﹣42;
(3)原式=﹣8××=﹣8;
(4)原式=×8﹣×﹣×=6﹣1﹣=;
(5)原式=﹣×﹣8÷2=﹣2﹣4=﹣6;
(6)原式=×(﹣36)﹣×(﹣36)+×(﹣36)=﹣8+9﹣2=1﹣2=﹣1;
(7)原式=﹣9×﹣[25×(﹣)﹣240×(﹣)×﹣2]
=﹣3﹣(﹣15+15﹣2)=﹣3+2=﹣1;
(8)原式=×(﹣)﹣×(﹣)=﹣1+1=0;
(9)原式=﹣1﹣××(2﹣9)=﹣1﹣×(﹣7)=﹣1+=;
(10)原式=﹣9﹣125×﹣18÷9=﹣9﹣20﹣2=﹣31;
(11)原式=﹣1﹣(﹣)×﹣8=﹣1+2﹣8=﹣7;
(12)原式=(37.15﹣47.65)×2﹣10.5×7
=﹣10.5×﹣10.5×
=﹣10.5×(+)
=﹣10.5×10
=﹣105.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
