2022-2023学年华师大版数学八年级上册12.3乘法公式同步达标测试题 (含答案)
文档属性
| 名称 | 2022-2023学年华师大版数学八年级上册12.3乘法公式同步达标测试题 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 116.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 11:37:14 | ||
图片预览



文档简介
2022-2023学年华东师大版八年级数学上册《12.3乘法公式》同步达标测试题(附答案)
一.选择题(共8小题,满分32分)
1.如果多项式x2+2x+k是完全平方式,则常数k的值为( )
A.1 B.﹣1 C.4 D.﹣4
2.如图所示,将四张全等的长方形硬纸片围成一个正方形,根据图形阴影部分面积的关系,可以直观地得到一个关于a、b的恒等式为( )
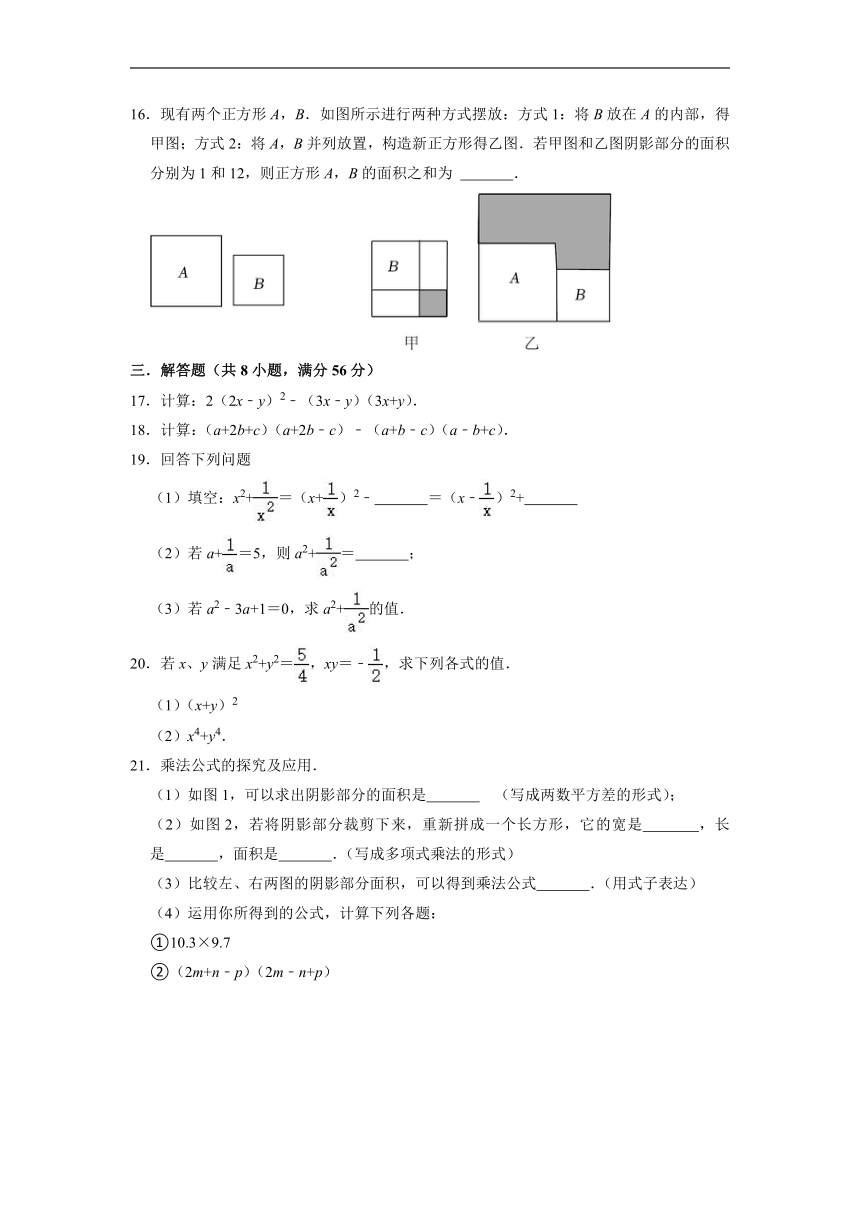
A.a2﹣b2=(a+b)(a﹣b) B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=(a+b)2﹣4ab D.a2+ab=a(a+b)
3.下列运算正确的是( )
A.(x+y)(y﹣x)=x2﹣y2 B.(﹣x+y)2=﹣x2+2xy+y2
C.(﹣x﹣y)2=﹣x2﹣2xy﹣y2 D.(x+y)(﹣y+x)=x2﹣y2
4.2×(3+1)(32+1)(34+1)(38+1)(316+1)+1的计算结果是( )
A.332+1 B.332﹣1 C.331 D.332
5.从前,一位农场主把一块边长为a米(a>4)的正方形土地租给租户张老汉,第二年,他对张老汉说:“我把这块地的一边增加4米,相邻的另一边减少4米,变成长方形土地继续租给你,租金不变,你也没有吃亏,你看如何?”如果这样,你觉得张老汉的租地面积会( )
A.没有变化 B.变大了 C.变小了 D.无法确定
6.若(a+b)2=25,a2+b2=13,则ab的值为( )
A.6 B.﹣6 C.12 D.﹣12
7.如图,点C是线段BG上的一点,以BC,CG为边向两边作正方形,面积分别是S1和S2,两正方形的面积和S1+S2=40,已知BG=8,则图中阴影部分面积为( )
A.6 B.8 C.10 D.12
8.若n满足关系式(n﹣2020)2+(2021﹣n)2=3,则代数式(n﹣2020)(2021﹣n)=( )
A.﹣1 B.0 C. D.1
二.填空题(共8小题,满分32分)
9.若x2﹣4x﹣1=(x+a)2﹣b,则|a﹣b|= .
10.如图,两个正方形的边长分别为a,b(a>b),若a+b=10,ab=6,则阴影部分的面积为 .
11.若(a+b)2=9,(a﹣b)2=4,则a2+b2= .
12.我们已经知道:
(a+b)0=1
(a+b)1=a+b
(a+b)2=a2+2ab+b2
再经过计算又可以知道:
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
将这些等式右边的系数从左到右进行排列,又得如图所示“三角形”形状,根据这个规律,猜测(a+b)5的结果是 .
13.若x2+2(m﹣3)x+9是完全平方式,则m的值等于 .
14.计算20222﹣2020×2024的结果是 .
15.如图,大正方形与小正方形的面积之差是40,则阴影部分的面积是 .
16.现有两个正方形A,B.如图所示进行两种方式摆放:方式1:将B放在A的内部,得甲图;方式2:将A,B并列放置,构造新正方形得乙图.若甲图和乙图阴影部分的面积分别为1和12,则正方形A,B的面积之和为 .
三.解答题(共8小题,满分56分)
17.计算:2(2x﹣y)2﹣(3x﹣y)(3x+y).
18.计算:(a+2b+c)(a+2b﹣c)﹣(a+b﹣c)(a﹣b+c).
19.回答下列问题
(1)填空:x2+=(x+)2﹣ =(x﹣)2+
(2)若a+=5,则a2+= ;
(3)若a2﹣3a+1=0,求a2+的值.
20.若x、y满足x2+y2=,xy=﹣,求下列各式的值.
(1)(x+y)2
(2)x4+y4.
21.乘法公式的探究及应用.
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个长方形,它的宽是 ,长是 ,面积是 .(写成多项式乘法的形式)
(3)比较左、右两图的阴影部分面积,可以得到乘法公式 .(用式子表达)
(4)运用你所得到的公式,计算下列各题:
①10.3×9.7
②(2m+n﹣p)(2m﹣n+p)
22.如图,边长为a的正方形中有一个边长为b(b<a)的小正方形,如图2是由图1中的阴影部分拼成的一个长方形.
(1)设图1阴影部分的面积为S1,图2中阴影部分的面积为S2,请直接用含a,b的式子表示S1= ,S2= ,写出上述过程中所揭示的乘法公式 ;
(2)直接应用,利用这个公式计算:
①(﹣x﹣y)(y﹣x);
②102×98.
(3)拓展应用,试利用这个公式求下面代数式的结果.
(3+1)×(32+1)×(34+1)×(38+1)×(316+1)×…×(31024+1)+1.
23.数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为a、宽为b的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系;
(2)若要拼出一个面积为(a+2b)(a+b)的矩形,则需要A号卡片1张,B号卡片2张,C号卡片 张.
(3)根据(1)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=11,求ab的值;
②已知(x﹣2019)2+(x﹣2021)2=20,求x﹣2020的值.
24.若x满足(x﹣4)(x﹣9)=6,求(x﹣4)2+(x﹣9)2的值.阅读下面求解的方法:
解:设(x﹣4)=a,(x﹣9)=b,则ab=(x﹣4)(x﹣9)=6,a﹣b=(x﹣4)﹣(x﹣9)=5
∴(x﹣4)2+(x﹣9)2=a2+b2=(a﹣b)2+2ab=52+2×6=37.
请仿照上面的方法求解下面的问题:
(1)若x满足(x﹣2)(x﹣5)=10,求(x﹣2)2+(x﹣5)2的值;
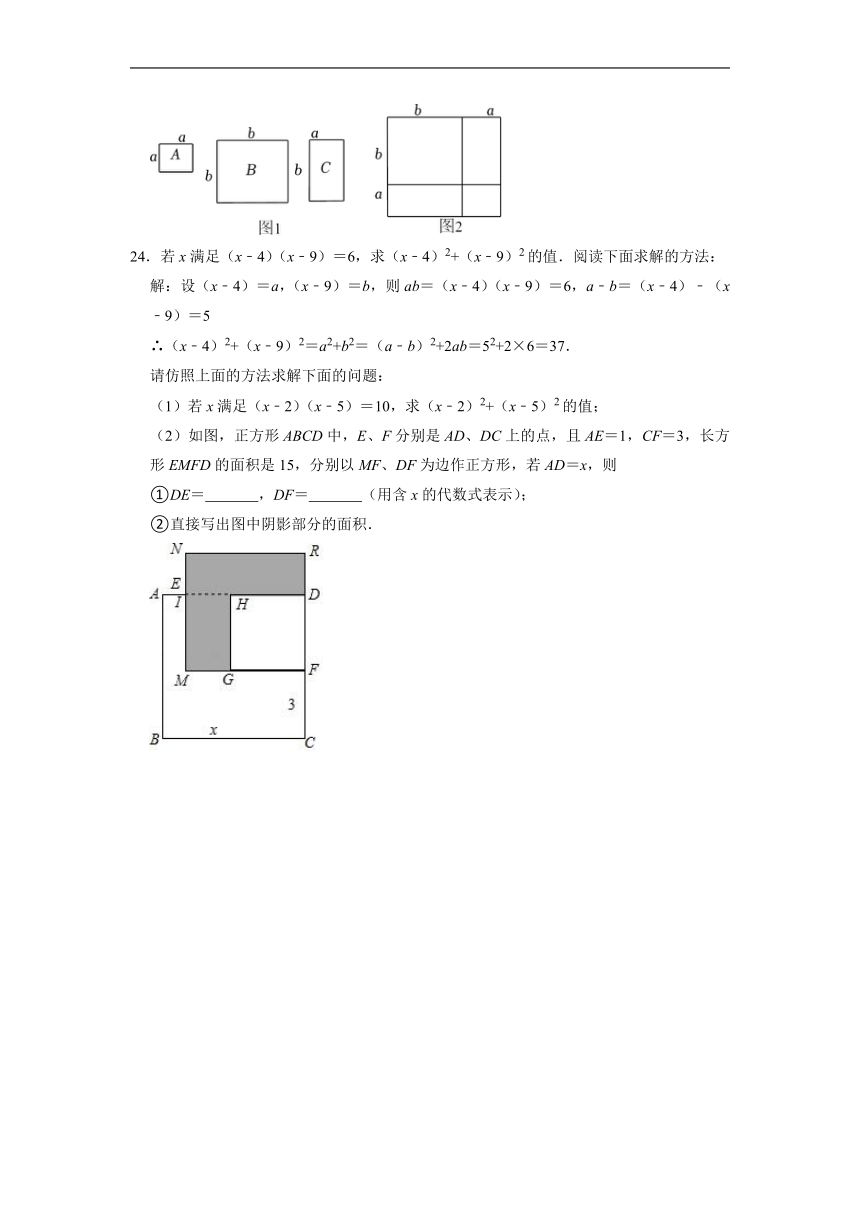
(2)如图,正方形ABCD中,E、F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是15,分别以MF、DF为边作正方形,若AD=x,则
①DE= ,DF= (用含x的代数式表示);
②直接写出图中阴影部分的面积.
参考答案
一.选择题(共8小题满分32分)
1.解:∵2x=2×1 x,
∴k=12=1,
故选A.
2.解:方法一阴影部分的面积为:(a﹣b)2,
方法二阴影部分的面积为:(a+b)2﹣4ab,
所以根据图形阴影部分面积的关系,可以直观地得到一个关于a、b的恒等式为(a﹣b)2=(a+b)2﹣4ab.
故选:C.
3.解:A、结果是y2﹣x2,故本选项不符合题意;
B、结果是x2﹣2xy+y2,故本选项不符合题意;
C、结果是x2+2xy+y2,故本选项不符合题意;
D、结果是x2﹣y2,故本选项符合题意;
故选:D.
4.解:2×(3+1)(32+1)(34+1)(38+1)(316+1)+1
=(3﹣1)(3+1)(32+1)(34+1)(38+1)(316+1)+1
=(32﹣1)(32+1)(34+1)(38+1)(316+1)+1
=(34﹣1)(34+1)(38+1)(316+1)+1
=(38﹣1)(38+1)(316+1)+1
=(316﹣1)(316+1)+1
=332﹣1+1
=332,
故选:D.
5.解:原来租的土地面积:a2(平方米).
现在租的土地面积:(a+4)(a﹣4)=a2﹣16(平方米).
∵a2>a2﹣16.
∴张老汉的租地面积会减少.
故选:C.
6.解:∵(a+b)2=a2+2ab+b2=25,a2+b2=13,
∴2ab=25﹣13=12,
∴ab=6,
故选:A.
7.解:设BC=a,CG=b,则S1=a2,S2=b2,a+b=BG=8.
∴a2+b2=40.
∵(a+b)2=a2+b2+2ab=64,
∴2ab=64﹣40=24,
∴ab=12,
∴阴影部分的面积等于ab=×12=6.
故选:A.
8.解:∵(n﹣2020)2+(2021﹣n)2=3,
∴(n﹣2020)2+2(n﹣2020)(2021﹣n)+(2021﹣n)2﹣2(n﹣2020)(2021﹣n)=﹣3,
∴1﹣2(n﹣2020)(2021﹣n)=3,
∴﹣2(n﹣2020)(2021﹣n)=2,
∴(n﹣2020)(2021﹣n)=﹣1,
故选:A.
二.填空题(共8小题,满分32分)
9.解:∵(x+a)2﹣b=x2+2ax+a2﹣b,
∴2a=﹣4,a2﹣b=﹣1,
解得a=﹣2,b=5,
∴|a﹣b|=|﹣2﹣5|=7.
故本题的答案是7.
10.解:S阴影=S大正方形+S小正方形﹣S△ABD﹣S△BEF
=a2+b2﹣a2﹣b(a+b)
=a2+b2﹣ab
=(a2+b2+2ab)﹣ab
=(a+b)2﹣ab
∵a+b=10,ab=6;
∴原式=×102﹣×6
=×100﹣9
=41
故答案为:41.
11.解:由完全平方公式(a+b)2=a2+2ab+b2和(a﹣b)2=a2﹣2ab+b2,可得,
∵(a+b)2=9,(a﹣b)2=4,
∴==6.5.
故答案为:6.5.
12.解:根据规律可知:(a+b)5的展开式中的系数分别为1、5、10、10、5、1.
∴(a+b)5的=a5+5a4b+10a3b2+10a2b3+5ab4+b5.
故答案为a5+5a4b+10a3b2+10a2b3+5ab4+b5.
13.解:∵x2+2(m﹣3)x+9是完全平方式,
∴m﹣3=±3,
解得:m=6或0.
故答案为:6或0.
14.解:20222﹣2020×2024
=20222﹣(2022﹣2)(2022+2)
=20222﹣(20222﹣22)
=20222﹣20222+22
=4.
故答案为:4.
15.解:设大正方形的边长为a,小正方形的边长为b,
根据题意得a2﹣b2=40,
∴(a+b)(a﹣b)=40;
∵S阴=S△ACD﹣S△CDE,
∴S阴=×CD×AB﹣×CD×BE
=(a+b)a﹣(a+b)b
=(a+b)(a﹣b)
∵(a+b)(a﹣b)=40,
∴S阴=×40
=20.
故答案为:20.
16.解:设正方形A的边长为a,正方形B的边长为b,
由图甲得a2﹣b2﹣2(a﹣b)b=1,
即a2+b2﹣2ab=1,
由图乙得(a+b)2﹣a2﹣b2=12,
得:2ab=12,
所以a2+b2=13,
故答案为:13.
三.解答题(共8小题,满分56分)
17.解:原式=2(4x2﹣4xy+y2)﹣9x2+y2
=8x2﹣8xy+2y2﹣9x2+y2
=﹣x2﹣8xy+3y2,
18.解:原式=(a+2b)2﹣c2﹣a2+(b﹣c)2
=a2+4ab+4b2﹣c2﹣a2+b2﹣2bc+c2
=4ab+5b2﹣2bc,
19.解:(1)2、2.
(2)23.
(3)∵a=0时方程不成立,
∴a≠0,
∵a2﹣3a+1=0
两边同除a得:a﹣3+=0,
移项得:a+=3,
∴a2+=(a+)2﹣2=7.
20.解:(1)∵x2+y2=,xy=﹣,
∴原式=x2+y2+2xy=﹣1=;
(2)∵x2+y2=,xy=﹣,
∴原式=(x2+y2)2﹣2x2y2=﹣=.
21.解:(1)利用正方形的面积公式可知:阴影部分的面积=a2﹣b2;
故答案为:a2﹣b2;
(2)由图可知矩形的宽是a﹣b,长是a+b,所以面积是(a+b)(a﹣b);
故答案为:a﹣b,a+b,(a+b)(a﹣b);
(3)(a+b)(a﹣b)=a2﹣b2(等式两边交换位置也可);
故答案为:(a+b)(a﹣b)=a2﹣b2;
(4)①解:原式=(10+0.3)×(10﹣0.3)
=102﹣0.32
=100﹣0.09
=99.91;
②解:原式=[2m+(n﹣p)] [2m﹣(n﹣p)]
=(2m)2﹣(n﹣p)2
=4m2﹣n2+2np﹣p2.
22.解:(1)S1=a2﹣b2,S2=(a+b)(a﹣b),
∵S1=S2,
∴a2﹣b2=(a+b)(a﹣b).
(2)①(﹣x﹣y)(y﹣x)=(﹣x)2﹣y2=x2﹣y2;
②102×98=(100+2)×(100﹣2)=9996.
(3)(3+1)×(32+1)×(34+1)×(38+1)×(316+1)......×(31024+1)+1,
=(3﹣1)×[(3+1)×(32+1)×(34+1)×(38+1)×(316+1)......×(31024+1)]÷(3﹣1)+1,
=(32﹣1)×(32+1)×(34+1)×(38+1)×(316+1)......×(31024+1)÷2+1,
=[(31024)2﹣12]÷2+1,
=(32048﹣1)÷2+1,
=.
23.解:(1)大正方形的面积可以表示为:(a+b)2,或表示为:a2+b2+2ab;
因此有(a+b)2=a2+b2+2ab;
(2)∵(a+2b)(a+b)=a2+3ab+2b2,
∴需要A号卡片1张,B号卡片2张,C号卡片3张,
故答案为:3;
(3)①∵(a+b)2=a2+b2+2ab,a+b=5,a2+b2=11,
∴25=11+2ab,
∴ab=7,
即ab的值为7;
②令a=x﹣2020,
∴x﹣2019
=[x﹣(2020﹣1)]
=x﹣2020+1
=a+1,
x﹣2021
=[x﹣(2020+1)]
=x﹣2020﹣1
=a﹣1,
∵(x﹣2019)2+(x﹣2021)2=20,
∴(a+1)2+(a﹣1)2=20,
解得a2=9.
∴(x﹣2020)2=9,
∴x﹣2020=±3.
24.解:(1)设(x﹣2)=a,(x﹣5)=b,则ab=(x﹣2)(x﹣5)=10,a﹣b=(x﹣2)﹣(x﹣5)=3,
∴(x﹣2)2+(x﹣5)2=a2+b2=(a﹣b)2+2ab=32+2×10=29;
(2)①∵AE=1,CF=3,正方形ABCD边长为x,
∴DE=x﹣1,DF=x﹣3.
故答案为:x﹣1,x﹣3;
②∵长方形EMFD的面积是15,
∴(x﹣1)(x﹣3)=15,
设x﹣1=a,x﹣3=b,则ab=15,a﹣b=2,
∴(x﹣1+x﹣3) =(a+b) =(a﹣b) +4ab=2 +4×15=64,
∵a≥0,b≥0,
∴x﹣1+x﹣3=a+b=8,
∴阴影部分面积为(x﹣1)2﹣(x﹣3)2=a ﹣b =(a+b)(a﹣b)=16.
一.选择题(共8小题,满分32分)
1.如果多项式x2+2x+k是完全平方式,则常数k的值为( )
A.1 B.﹣1 C.4 D.﹣4
2.如图所示,将四张全等的长方形硬纸片围成一个正方形,根据图形阴影部分面积的关系,可以直观地得到一个关于a、b的恒等式为( )
A.a2﹣b2=(a+b)(a﹣b) B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=(a+b)2﹣4ab D.a2+ab=a(a+b)
3.下列运算正确的是( )
A.(x+y)(y﹣x)=x2﹣y2 B.(﹣x+y)2=﹣x2+2xy+y2
C.(﹣x﹣y)2=﹣x2﹣2xy﹣y2 D.(x+y)(﹣y+x)=x2﹣y2
4.2×(3+1)(32+1)(34+1)(38+1)(316+1)+1的计算结果是( )
A.332+1 B.332﹣1 C.331 D.332
5.从前,一位农场主把一块边长为a米(a>4)的正方形土地租给租户张老汉,第二年,他对张老汉说:“我把这块地的一边增加4米,相邻的另一边减少4米,变成长方形土地继续租给你,租金不变,你也没有吃亏,你看如何?”如果这样,你觉得张老汉的租地面积会( )
A.没有变化 B.变大了 C.变小了 D.无法确定
6.若(a+b)2=25,a2+b2=13,则ab的值为( )
A.6 B.﹣6 C.12 D.﹣12
7.如图,点C是线段BG上的一点,以BC,CG为边向两边作正方形,面积分别是S1和S2,两正方形的面积和S1+S2=40,已知BG=8,则图中阴影部分面积为( )
A.6 B.8 C.10 D.12
8.若n满足关系式(n﹣2020)2+(2021﹣n)2=3,则代数式(n﹣2020)(2021﹣n)=( )
A.﹣1 B.0 C. D.1
二.填空题(共8小题,满分32分)
9.若x2﹣4x﹣1=(x+a)2﹣b,则|a﹣b|= .
10.如图,两个正方形的边长分别为a,b(a>b),若a+b=10,ab=6,则阴影部分的面积为 .
11.若(a+b)2=9,(a﹣b)2=4,则a2+b2= .
12.我们已经知道:
(a+b)0=1
(a+b)1=a+b
(a+b)2=a2+2ab+b2
再经过计算又可以知道:
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
将这些等式右边的系数从左到右进行排列,又得如图所示“三角形”形状,根据这个规律,猜测(a+b)5的结果是 .
13.若x2+2(m﹣3)x+9是完全平方式,则m的值等于 .
14.计算20222﹣2020×2024的结果是 .
15.如图,大正方形与小正方形的面积之差是40,则阴影部分的面积是 .
16.现有两个正方形A,B.如图所示进行两种方式摆放:方式1:将B放在A的内部,得甲图;方式2:将A,B并列放置,构造新正方形得乙图.若甲图和乙图阴影部分的面积分别为1和12,则正方形A,B的面积之和为 .
三.解答题(共8小题,满分56分)
17.计算:2(2x﹣y)2﹣(3x﹣y)(3x+y).
18.计算:(a+2b+c)(a+2b﹣c)﹣(a+b﹣c)(a﹣b+c).
19.回答下列问题
(1)填空:x2+=(x+)2﹣ =(x﹣)2+
(2)若a+=5,则a2+= ;
(3)若a2﹣3a+1=0,求a2+的值.
20.若x、y满足x2+y2=,xy=﹣,求下列各式的值.
(1)(x+y)2
(2)x4+y4.
21.乘法公式的探究及应用.
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个长方形,它的宽是 ,长是 ,面积是 .(写成多项式乘法的形式)
(3)比较左、右两图的阴影部分面积,可以得到乘法公式 .(用式子表达)
(4)运用你所得到的公式,计算下列各题:
①10.3×9.7
②(2m+n﹣p)(2m﹣n+p)
22.如图,边长为a的正方形中有一个边长为b(b<a)的小正方形,如图2是由图1中的阴影部分拼成的一个长方形.
(1)设图1阴影部分的面积为S1,图2中阴影部分的面积为S2,请直接用含a,b的式子表示S1= ,S2= ,写出上述过程中所揭示的乘法公式 ;
(2)直接应用,利用这个公式计算:
①(﹣x﹣y)(y﹣x);
②102×98.
(3)拓展应用,试利用这个公式求下面代数式的结果.
(3+1)×(32+1)×(34+1)×(38+1)×(316+1)×…×(31024+1)+1.
23.数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为a、宽为b的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系;
(2)若要拼出一个面积为(a+2b)(a+b)的矩形,则需要A号卡片1张,B号卡片2张,C号卡片 张.
(3)根据(1)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=11,求ab的值;
②已知(x﹣2019)2+(x﹣2021)2=20,求x﹣2020的值.
24.若x满足(x﹣4)(x﹣9)=6,求(x﹣4)2+(x﹣9)2的值.阅读下面求解的方法:
解:设(x﹣4)=a,(x﹣9)=b,则ab=(x﹣4)(x﹣9)=6,a﹣b=(x﹣4)﹣(x﹣9)=5
∴(x﹣4)2+(x﹣9)2=a2+b2=(a﹣b)2+2ab=52+2×6=37.
请仿照上面的方法求解下面的问题:
(1)若x满足(x﹣2)(x﹣5)=10,求(x﹣2)2+(x﹣5)2的值;
(2)如图,正方形ABCD中,E、F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是15,分别以MF、DF为边作正方形,若AD=x,则
①DE= ,DF= (用含x的代数式表示);
②直接写出图中阴影部分的面积.
参考答案
一.选择题(共8小题满分32分)
1.解:∵2x=2×1 x,
∴k=12=1,
故选A.
2.解:方法一阴影部分的面积为:(a﹣b)2,
方法二阴影部分的面积为:(a+b)2﹣4ab,
所以根据图形阴影部分面积的关系,可以直观地得到一个关于a、b的恒等式为(a﹣b)2=(a+b)2﹣4ab.
故选:C.
3.解:A、结果是y2﹣x2,故本选项不符合题意;
B、结果是x2﹣2xy+y2,故本选项不符合题意;
C、结果是x2+2xy+y2,故本选项不符合题意;
D、结果是x2﹣y2,故本选项符合题意;
故选:D.
4.解:2×(3+1)(32+1)(34+1)(38+1)(316+1)+1
=(3﹣1)(3+1)(32+1)(34+1)(38+1)(316+1)+1
=(32﹣1)(32+1)(34+1)(38+1)(316+1)+1
=(34﹣1)(34+1)(38+1)(316+1)+1
=(38﹣1)(38+1)(316+1)+1
=(316﹣1)(316+1)+1
=332﹣1+1
=332,
故选:D.
5.解:原来租的土地面积:a2(平方米).
现在租的土地面积:(a+4)(a﹣4)=a2﹣16(平方米).
∵a2>a2﹣16.
∴张老汉的租地面积会减少.
故选:C.
6.解:∵(a+b)2=a2+2ab+b2=25,a2+b2=13,
∴2ab=25﹣13=12,
∴ab=6,
故选:A.
7.解:设BC=a,CG=b,则S1=a2,S2=b2,a+b=BG=8.
∴a2+b2=40.
∵(a+b)2=a2+b2+2ab=64,
∴2ab=64﹣40=24,
∴ab=12,
∴阴影部分的面积等于ab=×12=6.
故选:A.
8.解:∵(n﹣2020)2+(2021﹣n)2=3,
∴(n﹣2020)2+2(n﹣2020)(2021﹣n)+(2021﹣n)2﹣2(n﹣2020)(2021﹣n)=﹣3,
∴1﹣2(n﹣2020)(2021﹣n)=3,
∴﹣2(n﹣2020)(2021﹣n)=2,
∴(n﹣2020)(2021﹣n)=﹣1,
故选:A.
二.填空题(共8小题,满分32分)
9.解:∵(x+a)2﹣b=x2+2ax+a2﹣b,
∴2a=﹣4,a2﹣b=﹣1,
解得a=﹣2,b=5,
∴|a﹣b|=|﹣2﹣5|=7.
故本题的答案是7.
10.解:S阴影=S大正方形+S小正方形﹣S△ABD﹣S△BEF
=a2+b2﹣a2﹣b(a+b)
=a2+b2﹣ab
=(a2+b2+2ab)﹣ab
=(a+b)2﹣ab
∵a+b=10,ab=6;
∴原式=×102﹣×6
=×100﹣9
=41
故答案为:41.
11.解:由完全平方公式(a+b)2=a2+2ab+b2和(a﹣b)2=a2﹣2ab+b2,可得,
∵(a+b)2=9,(a﹣b)2=4,
∴==6.5.
故答案为:6.5.
12.解:根据规律可知:(a+b)5的展开式中的系数分别为1、5、10、10、5、1.
∴(a+b)5的=a5+5a4b+10a3b2+10a2b3+5ab4+b5.
故答案为a5+5a4b+10a3b2+10a2b3+5ab4+b5.
13.解:∵x2+2(m﹣3)x+9是完全平方式,
∴m﹣3=±3,
解得:m=6或0.
故答案为:6或0.
14.解:20222﹣2020×2024
=20222﹣(2022﹣2)(2022+2)
=20222﹣(20222﹣22)
=20222﹣20222+22
=4.
故答案为:4.
15.解:设大正方形的边长为a,小正方形的边长为b,
根据题意得a2﹣b2=40,
∴(a+b)(a﹣b)=40;
∵S阴=S△ACD﹣S△CDE,
∴S阴=×CD×AB﹣×CD×BE
=(a+b)a﹣(a+b)b
=(a+b)(a﹣b)
∵(a+b)(a﹣b)=40,
∴S阴=×40
=20.
故答案为:20.
16.解:设正方形A的边长为a,正方形B的边长为b,
由图甲得a2﹣b2﹣2(a﹣b)b=1,
即a2+b2﹣2ab=1,
由图乙得(a+b)2﹣a2﹣b2=12,
得:2ab=12,
所以a2+b2=13,
故答案为:13.
三.解答题(共8小题,满分56分)
17.解:原式=2(4x2﹣4xy+y2)﹣9x2+y2
=8x2﹣8xy+2y2﹣9x2+y2
=﹣x2﹣8xy+3y2,
18.解:原式=(a+2b)2﹣c2﹣a2+(b﹣c)2
=a2+4ab+4b2﹣c2﹣a2+b2﹣2bc+c2
=4ab+5b2﹣2bc,
19.解:(1)2、2.
(2)23.
(3)∵a=0时方程不成立,
∴a≠0,
∵a2﹣3a+1=0
两边同除a得:a﹣3+=0,
移项得:a+=3,
∴a2+=(a+)2﹣2=7.
20.解:(1)∵x2+y2=,xy=﹣,
∴原式=x2+y2+2xy=﹣1=;
(2)∵x2+y2=,xy=﹣,
∴原式=(x2+y2)2﹣2x2y2=﹣=.
21.解:(1)利用正方形的面积公式可知:阴影部分的面积=a2﹣b2;
故答案为:a2﹣b2;
(2)由图可知矩形的宽是a﹣b,长是a+b,所以面积是(a+b)(a﹣b);
故答案为:a﹣b,a+b,(a+b)(a﹣b);
(3)(a+b)(a﹣b)=a2﹣b2(等式两边交换位置也可);
故答案为:(a+b)(a﹣b)=a2﹣b2;
(4)①解:原式=(10+0.3)×(10﹣0.3)
=102﹣0.32
=100﹣0.09
=99.91;
②解:原式=[2m+(n﹣p)] [2m﹣(n﹣p)]
=(2m)2﹣(n﹣p)2
=4m2﹣n2+2np﹣p2.
22.解:(1)S1=a2﹣b2,S2=(a+b)(a﹣b),
∵S1=S2,
∴a2﹣b2=(a+b)(a﹣b).
(2)①(﹣x﹣y)(y﹣x)=(﹣x)2﹣y2=x2﹣y2;
②102×98=(100+2)×(100﹣2)=9996.
(3)(3+1)×(32+1)×(34+1)×(38+1)×(316+1)......×(31024+1)+1,
=(3﹣1)×[(3+1)×(32+1)×(34+1)×(38+1)×(316+1)......×(31024+1)]÷(3﹣1)+1,
=(32﹣1)×(32+1)×(34+1)×(38+1)×(316+1)......×(31024+1)÷2+1,
=[(31024)2﹣12]÷2+1,
=(32048﹣1)÷2+1,
=.
23.解:(1)大正方形的面积可以表示为:(a+b)2,或表示为:a2+b2+2ab;
因此有(a+b)2=a2+b2+2ab;
(2)∵(a+2b)(a+b)=a2+3ab+2b2,
∴需要A号卡片1张,B号卡片2张,C号卡片3张,
故答案为:3;
(3)①∵(a+b)2=a2+b2+2ab,a+b=5,a2+b2=11,
∴25=11+2ab,
∴ab=7,
即ab的值为7;
②令a=x﹣2020,
∴x﹣2019
=[x﹣(2020﹣1)]
=x﹣2020+1
=a+1,
x﹣2021
=[x﹣(2020+1)]
=x﹣2020﹣1
=a﹣1,
∵(x﹣2019)2+(x﹣2021)2=20,
∴(a+1)2+(a﹣1)2=20,
解得a2=9.
∴(x﹣2020)2=9,
∴x﹣2020=±3.
24.解:(1)设(x﹣2)=a,(x﹣5)=b,则ab=(x﹣2)(x﹣5)=10,a﹣b=(x﹣2)﹣(x﹣5)=3,
∴(x﹣2)2+(x﹣5)2=a2+b2=(a﹣b)2+2ab=32+2×10=29;
(2)①∵AE=1,CF=3,正方形ABCD边长为x,
∴DE=x﹣1,DF=x﹣3.
故答案为:x﹣1,x﹣3;
②∵长方形EMFD的面积是15,
∴(x﹣1)(x﹣3)=15,
设x﹣1=a,x﹣3=b,则ab=15,a﹣b=2,
∴(x﹣1+x﹣3) =(a+b) =(a﹣b) +4ab=2 +4×15=64,
∵a≥0,b≥0,
∴x﹣1+x﹣3=a+b=8,
∴阴影部分面积为(x﹣1)2﹣(x﹣3)2=a ﹣b =(a+b)(a﹣b)=16.
