2022-2023学年华东师大版八年级数学上册12.3乘法公式 优生辅导练习题(含答案)
文档属性
| 名称 | 2022-2023学年华东师大版八年级数学上册12.3乘法公式 优生辅导练习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 233.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 07:31:53 | ||
图片预览




文档简介
2022-2023学年华东师大版八年级数学上册《12.3乘法公式》优生辅导练习题(附答案)
一.选择题
1.计算:(1﹣)×(1﹣)×(1﹣)×…×(1﹣)×(1﹣)的结果是( )
A. B. C. D.
2.(a+b)n(n为非负整数)当n=0,1,2,3,…时的展开情况如下所示:
(a+b)0=1
(a+b)1=a+b
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
观察上面式子的等号右边各项的系数,我们得到了如图所示:
这就是南宋数学家杨辉在其著作《详解九章算法》中列出的一个神奇的“图”,他揭示了(a+b)n展开后各项系数的情况,被后人称为“杨辉三角”.根据图,你认为(a+b)9展开式中所有项系数的和应该是( )
A.128 B.256 C.512 D.1024
3.图1,是一个长为2m、宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2形式拼成一个正方形,那么中间阴影部分的面积为( )
A.mn B.m2﹣n2 C.(m﹣n)2 D.(m+n)2
4.一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是( )
A.a2﹣4b2 B.(a﹣2b)2 C.2ab D.ab
5.如图,把一块面积为100的大长方形木板被分割成2个大小一样的大正方形①,1个小正方形②和2个大小一样的长方形③后,如图摆放,且每个小长方形③的面积为16,则标号为②的正方形的面积是( )
A.16 B.14 C.12 D.10
6.若x2+mx+25是完全平方式,则m的值是( )
A.±10 B.5 C.﹣10 D.±5
7.已知a+b=2,则a2﹣b2+4b的值为( )
A.0 B.1 C.3 D.4
8.如图,正方形ABCD的边长为x,其中AI=5,JC=3,两个阴影部分都是正方形且面积和为60,则重叠部分FJDI的面积为( )
A.28 B.29 C.30 D.31
9.如图,两个正方形边长分别为a、b,如果a+b=7,ab=10,则阴影部分的面积为( )
A.25 B.12.5 C.13 D.9.5
二.填空题
10.若a+b=8,ab=5,则a2+b2= .
11.计算:20232﹣2022×2024= .
12.已知m2+n2+10=6m﹣2n,则m﹣n= .
三.解答题
13.已知x+=3,求下列各式的值:
(1)(x﹣)2;
(2)x4+.
14.【初试锋芒】若x+y=8,x2+y2=40,求xy的值;
【再展风采】已知4a2+b2=57,ab=6,求2a+b的值;
【尽显才华】若(20﹣x)(x﹣30)=10,则(20﹣x)2+(x﹣30)2的值是 .
15.如图1,将边长为a的大正方形剪去一个边长为b的小正方形,然后将剩余部分拼成图2所示长方形.
(1)上述操作能验证的等式是 .
A.a2﹣2ab+b2=(a﹣b)2
B.a2﹣b2=(a+b)(a﹣b)
C.a2﹣ab=a(a﹣b)
(2)应用你从(1)中选出的等式,完成下列各题:
①已知x2﹣4y2=18,x﹣2y=3,求x+2y.
②计算:(1﹣)×(1﹣)×(1﹣)×……×(1﹣)×(1﹣).
16.两个边长分别为a和b的正方形如图放置(图①),其未叠合部分(阴影)面积为S1;若再在大正方形中的右下角摆放一个边长为b的小正方形(如图②),两个小正方形叠合部分(阴影)面积为S2.
(1)用含a、b的代数式分别表示S1、S2;
(2)若a﹣b=8,ab=13,求S1+S2的值;
(3)用a、b的代数式表示S3;并当S1+S2=34时,求出图③中阴影部分的面积S3.
17.如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).
(1)观察图1,长方形的周长是 ,面积是 ;
(2)观察图2,大正方形的边长是 ,小正方形的边长是 ;
(3)观察图2,请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 ;
(4)根据(3)中的结论,若x+y=5,x=4,求x﹣y的值.
18.现有长与宽分别为a、b的小长方形若干个,用两个这样的小长方形拼成如图1的图形,用四个相同的小长方形拼成图2的图形,请认真观察图形,解答下列问题:
(1)根据图中条件,请写出图1和图2所验证的关于a、b的关系式:(用含a、b的代数式表示出来);
图1表示: ;
图2表示: ;
根据上面的解题思路与方法,解决下列问题:
(2)若x+y=8,x2+y2=40,求xy的值;
(3)请直接写出下列问题答案:
①若2m+3n=5,mn=1,则2m﹣3n= ;
②若(4﹣m)(5﹣m)=6,则(4﹣m)2+(5﹣m)2= .
(4)如图3,点C是线段AB上的一点,以AC,BC为边向两边作正方形,设AB=7,两正方形的面积和S1+S2=16,求图中阴影部分面积.
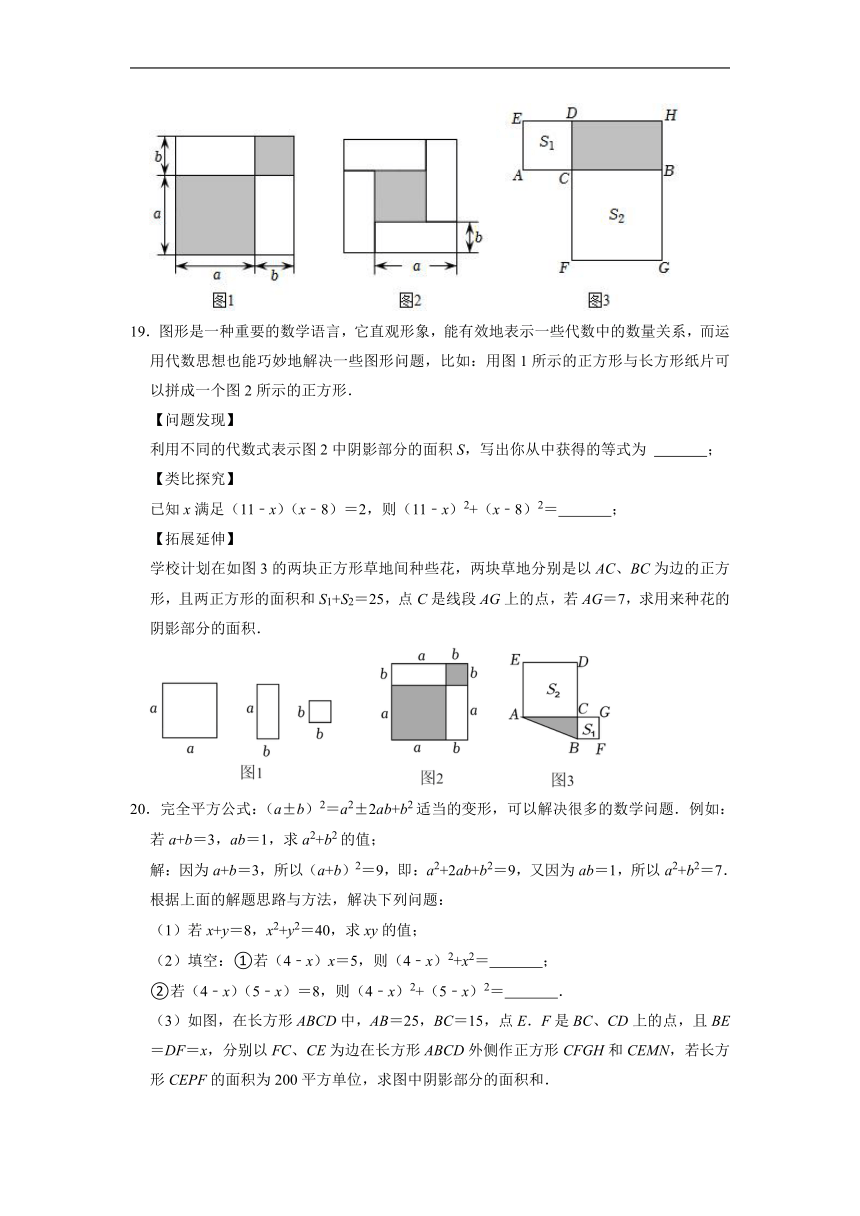
19.图形是一种重要的数学语言,它直观形象,能有效地表示一些代数中的数量关系,而运用代数思想也能巧妙地解决一些图形问题,比如:用图1所示的正方形与长方形纸片可以拼成一个图2所示的正方形.
【问题发现】
利用不同的代数式表示图2中阴影部分的面积S,写出你从中获得的等式为 ;
【类比探究】
已知x满足(11﹣x)(x﹣8)=2,则(11﹣x)2+(x﹣8)2= ;
【拓展延伸】
学校计划在如图3的两块正方形草地间种些花,两块草地分别是以AC、BC为边的正方形,且两正方形的面积和S1+S2=25,点C是线段AG上的点,若AG=7,求用来种花的阴影部分的面积.
20.完全平方公式:(a±b)2=a2±2ab+b2适当的变形,可以解决很多的数学问题.例如:若a+b=3,ab=1,求a2+b2的值;
解:因为a+b=3,所以(a+b)2=9,即:a2+2ab+b2=9,又因为ab=1,所以a2+b2=7.
根据上面的解题思路与方法,解决下列问题:
(1)若x+y=8,x2+y2=40,求xy的值;
(2)填空:①若(4﹣x)x=5,则(4﹣x)2+x2= ;
②若(4﹣x)(5﹣x)=8,则(4﹣x)2+(5﹣x)2= .
(3)如图,在长方形ABCD中,AB=25,BC=15,点E.F是BC、CD上的点,且BE=DF=x,分别以FC、CE为边在长方形ABCD外侧作正方形CFGH和CEMN,若长方形CEPF的面积为200平方单位,求图中阴影部分的面积和.
21.如图1是一个长为4a,宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个如图2的图形.
(1)观察图形,请你写出(a+b)2、(a﹣b)2、ab之间的等量关系式;
(2)若x+=3,利用(1)中的结论,求x﹣的值;
(3)若(2021﹣m)(2022﹣m)=4,求(m﹣2021)2+(2022﹣m)2的值.
22.利用完全平方公式(a±b)2=a2±2ab+b2,可以解决很多的数学问题.
例如:若a+b=3,ab=1,求a2+b2的值.
解:图为a+b=3,ab=1,
所以(a+b)2=9,
所以a2+b2+2ab=9.
所以a2+b2+2×1=9.
得a2+b2=7.
根据上面的解题思路与方法,解决下列问题:
(1)若x﹣y=4,x2+y2=40,求xy的值;
(2)若(2022﹣x)(x﹣2020)=﹣2021,求(2022﹣x)2+(x﹣2020)2的值.
23.图(1)是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图(2)的形状拼成一个正方形.
(1)你认为图(2)中阴影部分的正方形的边长是 (用m、n表示);
(2)请用两种不同的方法表示出图(2)中阴影部分的面积:①: ,②: ;
(3)观察图(2),请写出(m+n)2、(m﹣n)2、mn之间的一个等量关系 ;
(4)根据(3)中的等量关系,解决如下问题:若a+b=7,ab=6,求a﹣b的值.
24.我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”,如图所示,此图揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律.例如:(a+b)0=1,它只有1项,系数为1;(a+b)1=a+b,它有2项,系数分别为1,1,系数和为2;(a+b)2=a2+2ab+b2,它有3项系数分别为1,2,1,系数和为4;(a+b)3=a3+3a2b+3ab2+b3,它有4项,系数分别为1,3,3,1,系数和为8….
根据以上规律,解答下列问题.
(1)(a+b)4的展开式共有 项,系数分别为 .
(2)(a+b)n的展开式共有 项,系数和为 .
(3)计算:25+5×24+10×23+10×22+5×2+1.
参考答案
一.选择题
1.解:原式=(1﹣)×(1+)×(1﹣)×(1+)×(1﹣)×(1+)×…×(1﹣)×(1+)×(1﹣)×(1+)
=××××××…××××
=×
=.
故选:B.
2.解:当n=0时展开式所有系数的和为1=20.
当n=1时展开式所有系数的和为2=21.
当n=2时展开式所有系数的和为22.
当n=3时展开式所有系数的和为8=23.
当n=4时展开式所有系数的和为16=24.
当n=5时展开式所有系数的和为32=25.
……
∴当n=5时展开式所有系数的和为29=512.
故选:C.
3.解:方法一:
图2中四个长方形的面积的和=图1的长方形的面积=2m×2n=4mn,
图2的大正方形的面积=(m+n)2,
图2中阴影部分的面积=图2的大正方形的面积﹣图2中四个长方形的面积的和
=(m+n)2﹣4mn
=m2+2mn+n2﹣4mn
=m2﹣2mn+n2
=(m﹣n)2.
方法二:
图中阴影部分是正方形,且四个边长都是(m﹣n),
∴阴影部分的面积=(m﹣n)2.
故选:C.
4.解:由题意可知,小正方形的边长为,大正方形的边长为b+×2=,
所以阴影部分的面积为()2﹣()2×4=ab,
故选:D.
5.解:设标号为①的正方形的边长为x,标号为②的正方形的边长为y,则标号为③的长方形长为(x+y),宽为(x﹣y),
∵每个小长方形③的面积均为16,
∴(x+y)(x﹣y)=16,
∴x2﹣y2=16,
∴x2=16+y2
∵大长方形的长等于标号为③的小长方形的长与标号为①的正方形的边长的和,宽等于标号为③的小长方形的宽与标号为①的正方形的边长的和,
∴大长方形的长为:[(x+y)+x]=2x+y,宽为:[(x﹣y)+x]=2x﹣y,
∵大长方形的面积为100,
∴(2x+y)(2x﹣y)=100,
∴4x2﹣y2=100,
∴4(16+y2)﹣y2=100,
∴y2=12,
即标号为②的正方形的面积为y2=12.
故选:C.
6.解:∵x2+mx+25是完全平方式,且(±5)2=25,
∴x2+mx+25=(x±5)2=x2±2×1×5x+25=x2±10x+25,
∴m=±10,
故选:A.
7.解:当a+b=2时,
原式=(a+b)(a﹣b)+4b
=2(a﹣b)+4b
=2a﹣2b+4b
=2a+2b
=2(a+b)
=2×2
=4.
故选:D.
8.解:设ID=y,DJ=z,
∵两个阴影部分都是正方形,
∴DN=ID=x,DM=DJ=y,
∵四边形ABCD为正方形,
∴AD=CD,
∵AD=AI+ID,CD=CJ+DJ,
∴AI+ID=CJ+DJ,
∵AI=5,CJ=3,
∴5+y=3+z,
∴y=z﹣2,
:∵阴影部分面积和为60,
∴y2+z2=60,
方法1:将y=z﹣2代入y2+z2=60中,得:
(z﹣2)2+z2=60,
解得:z=1+或z=1﹣(舍),
∴y=z﹣2=﹣1,
∴ID=﹣1,DJ=1+,
∴S长方形FJDI=ID DJ=(﹣1)×(1+)=28;
方法2:∵z﹣y=2,
所以(z﹣y)2=4,
∴y2+z2﹣2yz=4,
∴60﹣2yz=4,
yz=28,
∴S长方形FJDI=ID DJ=28.
故选:A.
9.解:由题意知,阴影部分的面积=a2﹣﹣(a﹣b)b=a2+b2﹣ab=(a+b)2﹣ab,
∵a+b=7,ab=10,
∴阴影部分的面积=×72﹣×10==9.5,
故选:D.
二.填空题
10.解:∵(a+b)2=a2+2ab+b2,
又∵a+b=8,ab=5,
∴64=a2+b2+10,
∴a2+b2=54,
故答案为:54.
11.解:20232﹣2022×2024
=20232﹣(2023﹣1)(2023+1)
=20232﹣(20232﹣12)
=20232﹣20232+1
=1.
故答案为:1.
12.解:∵m2+n2+10=6m﹣2n,
∴m2﹣6m+9+n2+2n+1=0,
即(m﹣3)2+(n+1)2=0,
∴m=3,n=﹣1,
∴m﹣n=4,
故答案为:4.
三.解答题
13.解:(1)∵=
∴=
=
=﹣4x
=32﹣4
=5;
(2)∵=,
∴
=+2
=5+2
=7,
∵=,
∴
=﹣2
=49﹣2
=47.
14.解:(1)x+y=8,x2+y2=40,
xy=[(x+y)2﹣x2﹣y2]×=(82﹣40)×=12;
(2)4a2+b2=57,ab=6,
(2a+b)2=4a2+b2+4ab=81,
∴2a+b=±9;
(3)设a=20﹣x,b=x﹣30,
则(20﹣x)(x﹣30)=ab=10,
a+b=(20﹣x)+(x﹣30)=﹣10,
所以(20﹣x)2+(x﹣30)2
=a2+b2
=(a+b)2﹣2ab
=(﹣10)2﹣2×10
=80.
15.解:(1)根据阴影部分的面积相等得出:a2﹣b2=(a+b)(a﹣b).
故选:B.
(2)①∵x2﹣4y2=18,x﹣2y=3,
∴x+2y=(x2﹣4y2)÷(x﹣2y)=18÷3=6;
②原式=(1﹣)×(1+)×(1﹣)×(1+)×……×(1﹣)×(1+)
=××××……××
=×
=.
16.解:(1)图①中阴影部分的面积是边长为a、b的正方形的面积差,即S1=a2﹣b2;
图②中阴影部分是长为b,宽为2b﹣a的长方形,因此面积为:S2=b(2b﹣a)=2b2﹣ab;
(2)∵a﹣b=8,ab=13,
∴S1+S2=a2﹣b2+2b2﹣ab
=a2+b2﹣ab
=(a﹣b)2+ab
=64+13
=77;
(3)S3=a2+b2﹣a2﹣b(a+b)
=(a2+b2﹣ab),
当S1+S2=34时,即a2+b2﹣ab=34,
∴S3=(a2+b2﹣ab)=17.
17.解:(1)由长方形的周长、面积的计算公式可得,长方形的周长为8a+2b,面积为4ab,
故答案为:8a+2b,4ab;
(2)由拼图可得,大正方形的边长为a+b,小正方形的边长为b﹣a,
故答案为:a+b,b﹣a;
(3)由于S大正方形的面积=S阴影部分+4S长方形
∴(a+b)2=(b﹣a)2+4ab,
故答案为:(a+b)2=(b﹣a)2+4ab;
(4)∵x+y=5,x=4,
∴y=1,
∴x﹣y=4﹣1=3.
18.解:(1)图1中,由图可知S大正方形=(a+b)2,
S组成大正方形的四部分的面积之和=a2+b2+2ab,
由题意得,S大正方形=S组成大正方形的四部分的面积之和,
即(a+b)2=a2+b2+2ab,
故答案为:(a+b)2=a2+b2+2ab.
图2中,由图可知S大正方形=(a+b)2,S小正方形=(a﹣b)2,S四个长方形=4ab,
由题图可知,S大正方形=S小正方形+S四个长方形,
即(a+b)2=(a﹣b)2+4ab,
故答案为:(a+b)2=(a﹣b)2+4ab.
(2)∵(x+y)2=x2+y2+2xy,
∴xy=【(x+y)2﹣(x2+y2)】
∵x+y=8,x2+y2=40,
∴xy=(64﹣40)
=12.
(3)①由图2可得(2m﹣3n)2=(2m+3n)2﹣24mn,
∵2m+3n=5,mn=1,
∴(2m﹣3n)2=52﹣24=1,
∴2m﹣3n=±1.
故答案为:±1.
②由图1可得【(4﹣m)﹣(5﹣m)】2=(4﹣m)2+(5﹣m)2﹣2(4﹣m)(5﹣m),
∴(4﹣m)2+(5﹣m)2=【(4﹣m)﹣(5﹣m)】2+2(4﹣m)(5﹣m),
∵(4﹣m)(5﹣m)=6,
∴原式=1+2×6=13.
故答案为:13.
(4)由题意得AB=AC+CB,
∵AB=7,
∴AC+CB=7,
∵S1+S2=16,
∴AC2+CB2=16,
∵(AC+BC)2=AC2+CB2+2AC CB,
∴AC CB=[(AC+CB)2﹣(AC2+CB2)]
=(49﹣16)
=,
∴S阴影=CD CB=AC CB=.
即图中阴影部分的面积为.
19.解:【问题发现】根据面积的不同算法得:(a+b)2=a2+2ab+b2;
【类比探究】令a=11﹣x,b=x﹣8,
∴a+b=3,ab=2,
∵(a+b)2=a2+2ab+b2,
∴a2+b2=(a+b)2﹣2ab=9﹣4=5,
故答案为:5;
【拓展延伸】由题意得:AC+CG=7,AC2+CG2=25,
则2AC BC=2AC CG=(AC+CG)2﹣(AC2+CG2)=49﹣25=24,
∴阴影部分的面积为:AC BC=12.
20.解:(1)∵2xy=(x+y)2﹣(x2+y2)=64﹣40=26,
∴xy=13.
(2)①令a=4﹣x,b=x,
则a+b=4,ab=5,
∴a2+b2=(a+b)2﹣2ab=16﹣10=6.\,
∴(4﹣x)2+x2=6,
故答案为:6.
②令a=4﹣x,b=5﹣x,
则a﹣b=﹣1,ab=8,
∴a2+b2=(a﹣b)2+2ab=1+16=17,
∴(4﹣x)2+(5﹣x)2=17,
故答案为:17.
(3)由题意得:(25﹣x)(15﹣x)=200,
令a=25﹣x,b=15﹣x,
则:a﹣b=10,ab=200,
∴a2+b2=(a﹣b)2+2ab=100+400=500,
∴(25﹣x)2+(15﹣x)2=500,
所以阴影部分的面积和为500平方米.
21.解:(1)(a+b)2﹣(a﹣b)2=4ab.
观察图形知,图2中大正方形的面积为:(a+b)2,阴影面积为:(a﹣b)2,则图2中4个小长方形面积的和为:(a+b)2﹣(a﹣b)2;图1中4个小长方形面积的和为:4ab;由此得出:(a+b)2﹣(a﹣b)2=4ab.
(2)由(1)中的结论可知,(x+)2﹣(x﹣)2=4 x =4,
∵x+=3,
∴等号两边平方得,(x+)2=9,
∴(x﹣)2=(x+)2﹣4=9﹣4=5,
∴x﹣=±.
(3)(m﹣2021)2+(2022﹣m)2
=(2021﹣m)2+(2022﹣m)2
=[(2021﹣m)﹣(2022﹣m)]2+2(2021﹣m)(2022﹣m),
把(2021﹣m)(2022﹣m)=4代入,
原式=[2021﹣m﹣2022+m]2+2×4
=[﹣1]2+8
=1+8
=9.
22.解:(1)∵x﹣y=4,
∴(x﹣y)2=16,即x2﹣2xy+y2=16.
又∵x2+y2=40,
∴40﹣2xy=16,
解得xy=12,
答:xy的值是12;
(2)设2022﹣x=a,x﹣2020=b,则a+b=2.
∵(2022﹣x)(x﹣2020)=﹣2021,
∴ab=﹣2021,
把2022﹣x=a,x﹣2020=b,a+b=2代入得,
(2022﹣x)2+(x﹣2020)2
=(a+b)2﹣2ab
=22﹣2×(﹣2021)
=4+4042
=4046.
23.解:(1)图(2)中阴影部分的正方形的边长是m﹣n;
故答案为:m﹣n;
(2)请用两种不同的方法求图(2)中阴影部分面积.
①:(m﹣n)2;②:(m+n)2﹣4mn;
故答案为:(m﹣n)2,(m+n)2﹣4mn;
(3)观察图(2),(m+n)2、(m﹣n)2、mm之间的一个等量关系:
(m﹣n)2=(m+n)2﹣4mn;
故答案为:(m﹣n)2=(m+n)2﹣4mn;
(4)因为a+b=7,ab=6,
所以(a﹣b)2=(a+b)2﹣4ab
=72﹣4×6
=25,
所以a﹣b的值是±5.
24.解:(1)根据题意知,(a+b)4的展开后,共有5项,
各项系数分别为1、(1+3)、(3+3)、(3+1)、1,
即:1、4、6、4、1;
故答案为:5;1,4,6,4,1;
(2)根据题意,得(a+b)n的展开式共有(n+1)项,
(a+b)0的系数和为1=20,
(a+b)1的系数和为2=21,
(a+b)2的系数和为4=22,
(a+b)3的系数和为8=23,
,
由此规律可得,(a+b)n的系数和为2n.
∴(a+b)n的展开式共有(n+1)项,系数和为2n.
故答案为:(n+1),2n;
(3)25+5×24+10×23+10×22+5×2+1=(2+1)5=243.
一.选择题
1.计算:(1﹣)×(1﹣)×(1﹣)×…×(1﹣)×(1﹣)的结果是( )
A. B. C. D.
2.(a+b)n(n为非负整数)当n=0,1,2,3,…时的展开情况如下所示:
(a+b)0=1
(a+b)1=a+b
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
观察上面式子的等号右边各项的系数,我们得到了如图所示:
这就是南宋数学家杨辉在其著作《详解九章算法》中列出的一个神奇的“图”,他揭示了(a+b)n展开后各项系数的情况,被后人称为“杨辉三角”.根据图,你认为(a+b)9展开式中所有项系数的和应该是( )
A.128 B.256 C.512 D.1024
3.图1,是一个长为2m、宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2形式拼成一个正方形,那么中间阴影部分的面积为( )
A.mn B.m2﹣n2 C.(m﹣n)2 D.(m+n)2
4.一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是( )
A.a2﹣4b2 B.(a﹣2b)2 C.2ab D.ab
5.如图,把一块面积为100的大长方形木板被分割成2个大小一样的大正方形①,1个小正方形②和2个大小一样的长方形③后,如图摆放,且每个小长方形③的面积为16,则标号为②的正方形的面积是( )
A.16 B.14 C.12 D.10
6.若x2+mx+25是完全平方式,则m的值是( )
A.±10 B.5 C.﹣10 D.±5
7.已知a+b=2,则a2﹣b2+4b的值为( )
A.0 B.1 C.3 D.4
8.如图,正方形ABCD的边长为x,其中AI=5,JC=3,两个阴影部分都是正方形且面积和为60,则重叠部分FJDI的面积为( )
A.28 B.29 C.30 D.31
9.如图,两个正方形边长分别为a、b,如果a+b=7,ab=10,则阴影部分的面积为( )
A.25 B.12.5 C.13 D.9.5
二.填空题
10.若a+b=8,ab=5,则a2+b2= .
11.计算:20232﹣2022×2024= .
12.已知m2+n2+10=6m﹣2n,则m﹣n= .
三.解答题
13.已知x+=3,求下列各式的值:
(1)(x﹣)2;
(2)x4+.
14.【初试锋芒】若x+y=8,x2+y2=40,求xy的值;
【再展风采】已知4a2+b2=57,ab=6,求2a+b的值;
【尽显才华】若(20﹣x)(x﹣30)=10,则(20﹣x)2+(x﹣30)2的值是 .
15.如图1,将边长为a的大正方形剪去一个边长为b的小正方形,然后将剩余部分拼成图2所示长方形.
(1)上述操作能验证的等式是 .
A.a2﹣2ab+b2=(a﹣b)2
B.a2﹣b2=(a+b)(a﹣b)
C.a2﹣ab=a(a﹣b)
(2)应用你从(1)中选出的等式,完成下列各题:
①已知x2﹣4y2=18,x﹣2y=3,求x+2y.
②计算:(1﹣)×(1﹣)×(1﹣)×……×(1﹣)×(1﹣).
16.两个边长分别为a和b的正方形如图放置(图①),其未叠合部分(阴影)面积为S1;若再在大正方形中的右下角摆放一个边长为b的小正方形(如图②),两个小正方形叠合部分(阴影)面积为S2.
(1)用含a、b的代数式分别表示S1、S2;
(2)若a﹣b=8,ab=13,求S1+S2的值;
(3)用a、b的代数式表示S3;并当S1+S2=34时,求出图③中阴影部分的面积S3.
17.如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).
(1)观察图1,长方形的周长是 ,面积是 ;
(2)观察图2,大正方形的边长是 ,小正方形的边长是 ;
(3)观察图2,请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 ;
(4)根据(3)中的结论,若x+y=5,x=4,求x﹣y的值.
18.现有长与宽分别为a、b的小长方形若干个,用两个这样的小长方形拼成如图1的图形,用四个相同的小长方形拼成图2的图形,请认真观察图形,解答下列问题:
(1)根据图中条件,请写出图1和图2所验证的关于a、b的关系式:(用含a、b的代数式表示出来);
图1表示: ;
图2表示: ;
根据上面的解题思路与方法,解决下列问题:
(2)若x+y=8,x2+y2=40,求xy的值;
(3)请直接写出下列问题答案:
①若2m+3n=5,mn=1,则2m﹣3n= ;
②若(4﹣m)(5﹣m)=6,则(4﹣m)2+(5﹣m)2= .
(4)如图3,点C是线段AB上的一点,以AC,BC为边向两边作正方形,设AB=7,两正方形的面积和S1+S2=16,求图中阴影部分面积.
19.图形是一种重要的数学语言,它直观形象,能有效地表示一些代数中的数量关系,而运用代数思想也能巧妙地解决一些图形问题,比如:用图1所示的正方形与长方形纸片可以拼成一个图2所示的正方形.
【问题发现】
利用不同的代数式表示图2中阴影部分的面积S,写出你从中获得的等式为 ;
【类比探究】
已知x满足(11﹣x)(x﹣8)=2,则(11﹣x)2+(x﹣8)2= ;
【拓展延伸】
学校计划在如图3的两块正方形草地间种些花,两块草地分别是以AC、BC为边的正方形,且两正方形的面积和S1+S2=25,点C是线段AG上的点,若AG=7,求用来种花的阴影部分的面积.
20.完全平方公式:(a±b)2=a2±2ab+b2适当的变形,可以解决很多的数学问题.例如:若a+b=3,ab=1,求a2+b2的值;
解:因为a+b=3,所以(a+b)2=9,即:a2+2ab+b2=9,又因为ab=1,所以a2+b2=7.
根据上面的解题思路与方法,解决下列问题:
(1)若x+y=8,x2+y2=40,求xy的值;
(2)填空:①若(4﹣x)x=5,则(4﹣x)2+x2= ;
②若(4﹣x)(5﹣x)=8,则(4﹣x)2+(5﹣x)2= .
(3)如图,在长方形ABCD中,AB=25,BC=15,点E.F是BC、CD上的点,且BE=DF=x,分别以FC、CE为边在长方形ABCD外侧作正方形CFGH和CEMN,若长方形CEPF的面积为200平方单位,求图中阴影部分的面积和.
21.如图1是一个长为4a,宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个如图2的图形.
(1)观察图形,请你写出(a+b)2、(a﹣b)2、ab之间的等量关系式;
(2)若x+=3,利用(1)中的结论,求x﹣的值;
(3)若(2021﹣m)(2022﹣m)=4,求(m﹣2021)2+(2022﹣m)2的值.
22.利用完全平方公式(a±b)2=a2±2ab+b2,可以解决很多的数学问题.
例如:若a+b=3,ab=1,求a2+b2的值.
解:图为a+b=3,ab=1,
所以(a+b)2=9,
所以a2+b2+2ab=9.
所以a2+b2+2×1=9.
得a2+b2=7.
根据上面的解题思路与方法,解决下列问题:
(1)若x﹣y=4,x2+y2=40,求xy的值;
(2)若(2022﹣x)(x﹣2020)=﹣2021,求(2022﹣x)2+(x﹣2020)2的值.
23.图(1)是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图(2)的形状拼成一个正方形.
(1)你认为图(2)中阴影部分的正方形的边长是 (用m、n表示);
(2)请用两种不同的方法表示出图(2)中阴影部分的面积:①: ,②: ;
(3)观察图(2),请写出(m+n)2、(m﹣n)2、mn之间的一个等量关系 ;
(4)根据(3)中的等量关系,解决如下问题:若a+b=7,ab=6,求a﹣b的值.
24.我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”,如图所示,此图揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律.例如:(a+b)0=1,它只有1项,系数为1;(a+b)1=a+b,它有2项,系数分别为1,1,系数和为2;(a+b)2=a2+2ab+b2,它有3项系数分别为1,2,1,系数和为4;(a+b)3=a3+3a2b+3ab2+b3,它有4项,系数分别为1,3,3,1,系数和为8….
根据以上规律,解答下列问题.
(1)(a+b)4的展开式共有 项,系数分别为 .
(2)(a+b)n的展开式共有 项,系数和为 .
(3)计算:25+5×24+10×23+10×22+5×2+1.
参考答案
一.选择题
1.解:原式=(1﹣)×(1+)×(1﹣)×(1+)×(1﹣)×(1+)×…×(1﹣)×(1+)×(1﹣)×(1+)
=××××××…××××
=×
=.
故选:B.
2.解:当n=0时展开式所有系数的和为1=20.
当n=1时展开式所有系数的和为2=21.
当n=2时展开式所有系数的和为22.
当n=3时展开式所有系数的和为8=23.
当n=4时展开式所有系数的和为16=24.
当n=5时展开式所有系数的和为32=25.
……
∴当n=5时展开式所有系数的和为29=512.
故选:C.
3.解:方法一:
图2中四个长方形的面积的和=图1的长方形的面积=2m×2n=4mn,
图2的大正方形的面积=(m+n)2,
图2中阴影部分的面积=图2的大正方形的面积﹣图2中四个长方形的面积的和
=(m+n)2﹣4mn
=m2+2mn+n2﹣4mn
=m2﹣2mn+n2
=(m﹣n)2.
方法二:
图中阴影部分是正方形,且四个边长都是(m﹣n),
∴阴影部分的面积=(m﹣n)2.
故选:C.
4.解:由题意可知,小正方形的边长为,大正方形的边长为b+×2=,
所以阴影部分的面积为()2﹣()2×4=ab,
故选:D.
5.解:设标号为①的正方形的边长为x,标号为②的正方形的边长为y,则标号为③的长方形长为(x+y),宽为(x﹣y),
∵每个小长方形③的面积均为16,
∴(x+y)(x﹣y)=16,
∴x2﹣y2=16,
∴x2=16+y2
∵大长方形的长等于标号为③的小长方形的长与标号为①的正方形的边长的和,宽等于标号为③的小长方形的宽与标号为①的正方形的边长的和,
∴大长方形的长为:[(x+y)+x]=2x+y,宽为:[(x﹣y)+x]=2x﹣y,
∵大长方形的面积为100,
∴(2x+y)(2x﹣y)=100,
∴4x2﹣y2=100,
∴4(16+y2)﹣y2=100,
∴y2=12,
即标号为②的正方形的面积为y2=12.
故选:C.
6.解:∵x2+mx+25是完全平方式,且(±5)2=25,
∴x2+mx+25=(x±5)2=x2±2×1×5x+25=x2±10x+25,
∴m=±10,
故选:A.
7.解:当a+b=2时,
原式=(a+b)(a﹣b)+4b
=2(a﹣b)+4b
=2a﹣2b+4b
=2a+2b
=2(a+b)
=2×2
=4.
故选:D.
8.解:设ID=y,DJ=z,
∵两个阴影部分都是正方形,
∴DN=ID=x,DM=DJ=y,
∵四边形ABCD为正方形,
∴AD=CD,
∵AD=AI+ID,CD=CJ+DJ,
∴AI+ID=CJ+DJ,
∵AI=5,CJ=3,
∴5+y=3+z,
∴y=z﹣2,
:∵阴影部分面积和为60,
∴y2+z2=60,
方法1:将y=z﹣2代入y2+z2=60中,得:
(z﹣2)2+z2=60,
解得:z=1+或z=1﹣(舍),
∴y=z﹣2=﹣1,
∴ID=﹣1,DJ=1+,
∴S长方形FJDI=ID DJ=(﹣1)×(1+)=28;
方法2:∵z﹣y=2,
所以(z﹣y)2=4,
∴y2+z2﹣2yz=4,
∴60﹣2yz=4,
yz=28,
∴S长方形FJDI=ID DJ=28.
故选:A.
9.解:由题意知,阴影部分的面积=a2﹣﹣(a﹣b)b=a2+b2﹣ab=(a+b)2﹣ab,
∵a+b=7,ab=10,
∴阴影部分的面积=×72﹣×10==9.5,
故选:D.
二.填空题
10.解:∵(a+b)2=a2+2ab+b2,
又∵a+b=8,ab=5,
∴64=a2+b2+10,
∴a2+b2=54,
故答案为:54.
11.解:20232﹣2022×2024
=20232﹣(2023﹣1)(2023+1)
=20232﹣(20232﹣12)
=20232﹣20232+1
=1.
故答案为:1.
12.解:∵m2+n2+10=6m﹣2n,
∴m2﹣6m+9+n2+2n+1=0,
即(m﹣3)2+(n+1)2=0,
∴m=3,n=﹣1,
∴m﹣n=4,
故答案为:4.
三.解答题
13.解:(1)∵=
∴=
=
=﹣4x
=32﹣4
=5;
(2)∵=,
∴
=+2
=5+2
=7,
∵=,
∴
=﹣2
=49﹣2
=47.
14.解:(1)x+y=8,x2+y2=40,
xy=[(x+y)2﹣x2﹣y2]×=(82﹣40)×=12;
(2)4a2+b2=57,ab=6,
(2a+b)2=4a2+b2+4ab=81,
∴2a+b=±9;
(3)设a=20﹣x,b=x﹣30,
则(20﹣x)(x﹣30)=ab=10,
a+b=(20﹣x)+(x﹣30)=﹣10,
所以(20﹣x)2+(x﹣30)2
=a2+b2
=(a+b)2﹣2ab
=(﹣10)2﹣2×10
=80.
15.解:(1)根据阴影部分的面积相等得出:a2﹣b2=(a+b)(a﹣b).
故选:B.
(2)①∵x2﹣4y2=18,x﹣2y=3,
∴x+2y=(x2﹣4y2)÷(x﹣2y)=18÷3=6;
②原式=(1﹣)×(1+)×(1﹣)×(1+)×……×(1﹣)×(1+)
=××××……××
=×
=.
16.解:(1)图①中阴影部分的面积是边长为a、b的正方形的面积差,即S1=a2﹣b2;
图②中阴影部分是长为b,宽为2b﹣a的长方形,因此面积为:S2=b(2b﹣a)=2b2﹣ab;
(2)∵a﹣b=8,ab=13,
∴S1+S2=a2﹣b2+2b2﹣ab
=a2+b2﹣ab
=(a﹣b)2+ab
=64+13
=77;
(3)S3=a2+b2﹣a2﹣b(a+b)
=(a2+b2﹣ab),
当S1+S2=34时,即a2+b2﹣ab=34,
∴S3=(a2+b2﹣ab)=17.
17.解:(1)由长方形的周长、面积的计算公式可得,长方形的周长为8a+2b,面积为4ab,
故答案为:8a+2b,4ab;
(2)由拼图可得,大正方形的边长为a+b,小正方形的边长为b﹣a,
故答案为:a+b,b﹣a;
(3)由于S大正方形的面积=S阴影部分+4S长方形
∴(a+b)2=(b﹣a)2+4ab,
故答案为:(a+b)2=(b﹣a)2+4ab;
(4)∵x+y=5,x=4,
∴y=1,
∴x﹣y=4﹣1=3.
18.解:(1)图1中,由图可知S大正方形=(a+b)2,
S组成大正方形的四部分的面积之和=a2+b2+2ab,
由题意得,S大正方形=S组成大正方形的四部分的面积之和,
即(a+b)2=a2+b2+2ab,
故答案为:(a+b)2=a2+b2+2ab.
图2中,由图可知S大正方形=(a+b)2,S小正方形=(a﹣b)2,S四个长方形=4ab,
由题图可知,S大正方形=S小正方形+S四个长方形,
即(a+b)2=(a﹣b)2+4ab,
故答案为:(a+b)2=(a﹣b)2+4ab.
(2)∵(x+y)2=x2+y2+2xy,
∴xy=【(x+y)2﹣(x2+y2)】
∵x+y=8,x2+y2=40,
∴xy=(64﹣40)
=12.
(3)①由图2可得(2m﹣3n)2=(2m+3n)2﹣24mn,
∵2m+3n=5,mn=1,
∴(2m﹣3n)2=52﹣24=1,
∴2m﹣3n=±1.
故答案为:±1.
②由图1可得【(4﹣m)﹣(5﹣m)】2=(4﹣m)2+(5﹣m)2﹣2(4﹣m)(5﹣m),
∴(4﹣m)2+(5﹣m)2=【(4﹣m)﹣(5﹣m)】2+2(4﹣m)(5﹣m),
∵(4﹣m)(5﹣m)=6,
∴原式=1+2×6=13.
故答案为:13.
(4)由题意得AB=AC+CB,
∵AB=7,
∴AC+CB=7,
∵S1+S2=16,
∴AC2+CB2=16,
∵(AC+BC)2=AC2+CB2+2AC CB,
∴AC CB=[(AC+CB)2﹣(AC2+CB2)]
=(49﹣16)
=,
∴S阴影=CD CB=AC CB=.
即图中阴影部分的面积为.
19.解:【问题发现】根据面积的不同算法得:(a+b)2=a2+2ab+b2;
【类比探究】令a=11﹣x,b=x﹣8,
∴a+b=3,ab=2,
∵(a+b)2=a2+2ab+b2,
∴a2+b2=(a+b)2﹣2ab=9﹣4=5,
故答案为:5;
【拓展延伸】由题意得:AC+CG=7,AC2+CG2=25,
则2AC BC=2AC CG=(AC+CG)2﹣(AC2+CG2)=49﹣25=24,
∴阴影部分的面积为:AC BC=12.
20.解:(1)∵2xy=(x+y)2﹣(x2+y2)=64﹣40=26,
∴xy=13.
(2)①令a=4﹣x,b=x,
则a+b=4,ab=5,
∴a2+b2=(a+b)2﹣2ab=16﹣10=6.\,
∴(4﹣x)2+x2=6,
故答案为:6.
②令a=4﹣x,b=5﹣x,
则a﹣b=﹣1,ab=8,
∴a2+b2=(a﹣b)2+2ab=1+16=17,
∴(4﹣x)2+(5﹣x)2=17,
故答案为:17.
(3)由题意得:(25﹣x)(15﹣x)=200,
令a=25﹣x,b=15﹣x,
则:a﹣b=10,ab=200,
∴a2+b2=(a﹣b)2+2ab=100+400=500,
∴(25﹣x)2+(15﹣x)2=500,
所以阴影部分的面积和为500平方米.
21.解:(1)(a+b)2﹣(a﹣b)2=4ab.
观察图形知,图2中大正方形的面积为:(a+b)2,阴影面积为:(a﹣b)2,则图2中4个小长方形面积的和为:(a+b)2﹣(a﹣b)2;图1中4个小长方形面积的和为:4ab;由此得出:(a+b)2﹣(a﹣b)2=4ab.
(2)由(1)中的结论可知,(x+)2﹣(x﹣)2=4 x =4,
∵x+=3,
∴等号两边平方得,(x+)2=9,
∴(x﹣)2=(x+)2﹣4=9﹣4=5,
∴x﹣=±.
(3)(m﹣2021)2+(2022﹣m)2
=(2021﹣m)2+(2022﹣m)2
=[(2021﹣m)﹣(2022﹣m)]2+2(2021﹣m)(2022﹣m),
把(2021﹣m)(2022﹣m)=4代入,
原式=[2021﹣m﹣2022+m]2+2×4
=[﹣1]2+8
=1+8
=9.
22.解:(1)∵x﹣y=4,
∴(x﹣y)2=16,即x2﹣2xy+y2=16.
又∵x2+y2=40,
∴40﹣2xy=16,
解得xy=12,
答:xy的值是12;
(2)设2022﹣x=a,x﹣2020=b,则a+b=2.
∵(2022﹣x)(x﹣2020)=﹣2021,
∴ab=﹣2021,
把2022﹣x=a,x﹣2020=b,a+b=2代入得,
(2022﹣x)2+(x﹣2020)2
=(a+b)2﹣2ab
=22﹣2×(﹣2021)
=4+4042
=4046.
23.解:(1)图(2)中阴影部分的正方形的边长是m﹣n;
故答案为:m﹣n;
(2)请用两种不同的方法求图(2)中阴影部分面积.
①:(m﹣n)2;②:(m+n)2﹣4mn;
故答案为:(m﹣n)2,(m+n)2﹣4mn;
(3)观察图(2),(m+n)2、(m﹣n)2、mm之间的一个等量关系:
(m﹣n)2=(m+n)2﹣4mn;
故答案为:(m﹣n)2=(m+n)2﹣4mn;
(4)因为a+b=7,ab=6,
所以(a﹣b)2=(a+b)2﹣4ab
=72﹣4×6
=25,
所以a﹣b的值是±5.
24.解:(1)根据题意知,(a+b)4的展开后,共有5项,
各项系数分别为1、(1+3)、(3+3)、(3+1)、1,
即:1、4、6、4、1;
故答案为:5;1,4,6,4,1;
(2)根据题意,得(a+b)n的展开式共有(n+1)项,
(a+b)0的系数和为1=20,
(a+b)1的系数和为2=21,
(a+b)2的系数和为4=22,
(a+b)3的系数和为8=23,
,
由此规律可得,(a+b)n的系数和为2n.
∴(a+b)n的展开式共有(n+1)项,系数和为2n.
故答案为:(n+1),2n;
(3)25+5×24+10×23+10×22+5×2+1=(2+1)5=243.
