2022—2023学年人教版数学八年级上册11.2.2三角形的外角 导学案(含简略答案)
文档属性
| 名称 | 2022—2023学年人教版数学八年级上册11.2.2三角形的外角 导学案(含简略答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 437.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 23:00:47 | ||
图片预览


文档简介
11.2.2三角形的外角
班级: 组号: 姓名:
一、旧知回顾
1.画图说明什么是邻补角?互为邻补角的两个角的度数之和是多少度?
2.如图两直线相交,共有几对邻补角,请根据图中所给的字母把互为邻补角写出来。
二、新知梳理
3.学习三角形的外角定义时,要注意的是另一边的延长线是什么意思;如图, 是的外角;每个顶点处对应 个外角,这两个是 角。一个三角形共有 个外角。
三、试一试
4.写出下列图形中和度数:
∠1= , ∠1= , ∠1= , ∠1= ,
∠2= 。 ∠2= 。 ∠2= 。 ∠2= 。
5.如图,D是AB上一点,E是AC上一点,BE、CD相交于点F,,,,求和的度数。
★通过预习你还有什么困惑?
精练反馈
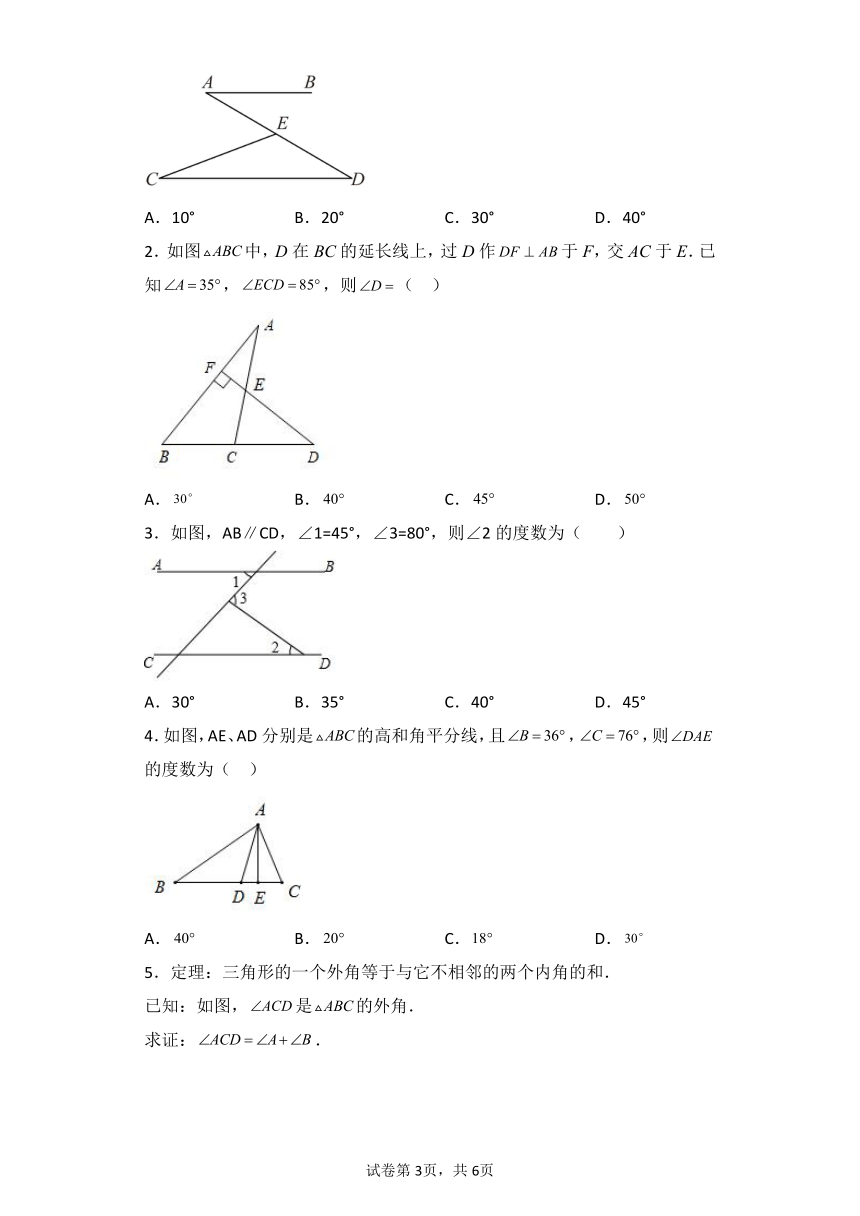
1.如图,已知,点E在线段AD上(不与点A,点D重合),连接CE.若∠C=20°,∠AEC=50°,则∠A=( )
A.10° B.20° C.30° D.40°
2.如图中,D在BC的延长线上,过D作于F,交AC于E.已知,,则( )
A. B. C. D.
3.如图,AB∥CD,∠1=45°,∠3=80°,则∠2的度数为( )
A.30° B.35° C.40° D.45°
4.如图,AE、AD分别是的高和角平分线,且,,则的度数为( )
A. B. C. D.
5.定理:三角形的一个外角等于与它不相邻的两个内角的和.
已知:如图,是的外角.
求证:.
下列说法正确的是( )
A.证法1还需证明其他形状的三角形,该定理的证明才完整
B.证法1用严谨的推理证明了该定理
C.证法2用特殊到一般法证明了该定理
D.证法2只要测量够一百个三角形进行验证,就能证明该定理
6.如图,BE、CE分别为的内、外角平分线,BF、CF分别为的内、外角平分线,若,则_______度.
7.如图,BE、CF是△ABC的角平分线,BE、CF相交于点D,若,则∠CDE的度数为______°.
8.三角形的一个外角是100°,则与它不相邻的两内角平分线夹角(钝角)是 _____.
9.如图,在中,,,于D,点E为BC边上一点,连接AE.把沿着AE对折后,点B的对应点刚好落在AC边上的点F处.
(1)求∠FEC的度数;
(2)求∠DAE的度数.
10.已知:如图,点E在AC上,点F在AB上,BE、CF交于点O,且,,求的度数.
11.如图,CE平分,F为CA延长线上一点,交AB于点G,,,求的度数.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
2.B
3.B
4.B
5.B
6.13
7.60;
8.130°
9.(1)
(2)
10.45°
11.25°
5 / 5
班级: 组号: 姓名:
一、旧知回顾
1.画图说明什么是邻补角?互为邻补角的两个角的度数之和是多少度?
2.如图两直线相交,共有几对邻补角,请根据图中所给的字母把互为邻补角写出来。
二、新知梳理
3.学习三角形的外角定义时,要注意的是另一边的延长线是什么意思;如图, 是的外角;每个顶点处对应 个外角,这两个是 角。一个三角形共有 个外角。
三、试一试
4.写出下列图形中和度数:
∠1= , ∠1= , ∠1= , ∠1= ,
∠2= 。 ∠2= 。 ∠2= 。 ∠2= 。
5.如图,D是AB上一点,E是AC上一点,BE、CD相交于点F,,,,求和的度数。
★通过预习你还有什么困惑?
精练反馈
1.如图,已知,点E在线段AD上(不与点A,点D重合),连接CE.若∠C=20°,∠AEC=50°,则∠A=( )
A.10° B.20° C.30° D.40°
2.如图中,D在BC的延长线上,过D作于F,交AC于E.已知,,则( )
A. B. C. D.
3.如图,AB∥CD,∠1=45°,∠3=80°,则∠2的度数为( )
A.30° B.35° C.40° D.45°
4.如图,AE、AD分别是的高和角平分线,且,,则的度数为( )
A. B. C. D.
5.定理:三角形的一个外角等于与它不相邻的两个内角的和.
已知:如图,是的外角.
求证:.
下列说法正确的是( )
A.证法1还需证明其他形状的三角形,该定理的证明才完整
B.证法1用严谨的推理证明了该定理
C.证法2用特殊到一般法证明了该定理
D.证法2只要测量够一百个三角形进行验证,就能证明该定理
6.如图,BE、CE分别为的内、外角平分线,BF、CF分别为的内、外角平分线,若,则_______度.
7.如图,BE、CF是△ABC的角平分线,BE、CF相交于点D,若,则∠CDE的度数为______°.
8.三角形的一个外角是100°,则与它不相邻的两内角平分线夹角(钝角)是 _____.
9.如图,在中,,,于D,点E为BC边上一点,连接AE.把沿着AE对折后,点B的对应点刚好落在AC边上的点F处.
(1)求∠FEC的度数;
(2)求∠DAE的度数.
10.已知:如图,点E在AC上,点F在AB上,BE、CF交于点O,且,,求的度数.
11.如图,CE平分,F为CA延长线上一点,交AB于点G,,,求的度数.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
2.B
3.B
4.B
5.B
6.13
7.60;
8.130°
9.(1)
(2)
10.45°
11.25°
5 / 5
