2022—2023学年人教版数学八年级上册11.3.2多边形的内角和 导学案(表格式,含简略答案)
文档属性
| 名称 | 2022—2023学年人教版数学八年级上册11.3.2多边形的内角和 导学案(表格式,含简略答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 79.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 00:00:00 | ||
图片预览

文档简介
11.3.2多边形的内角和
学 习目 标 1.能记住多边形的内角和、外角和的概念。2.能通过不同方法推导多边形的内角和与外角和公式,进一步体会数学化归思想。3.能熟练运用多边形的内角和与外角和公式进行有关计算
学 习方 法 合作交流、讨论
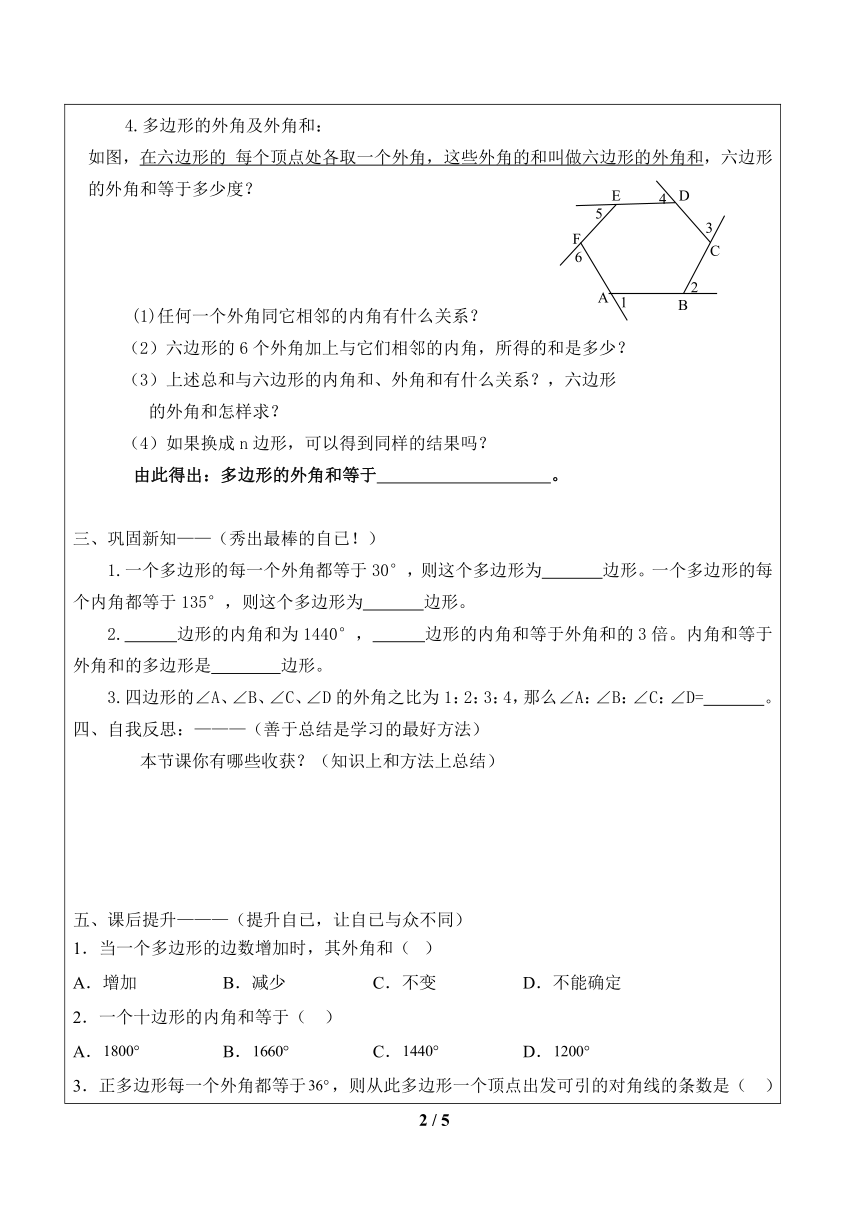
一、自主学习——(相信自已,一定行!)1.我们知道三角形的内角和为__________。2.我们还知道,正方形的四个角都等于____。,那么它的内角和为_____。,同样长方形的内角和也是_______。 3.正方形和长方形都是特殊的四边形,其内角和为360°,那么一般的四边形的内角和为多少呢?二、合作交流——(集体的智慧是无穷的,携手解决下面的问题吧!)1.从四边形的一个顶点出发可以引 条对角线?它们将四边形分成 个三角形?那么四边 形的内角和等于 度?你是怎么得到的?刚才我们是以某一个顶点来分割原图形成若干个三角形,还能在其它地方取点采取同样的方法吗?2.从五边形一个顶点出发可以引 条对角线?它们将五边形分成 个三角形?那么这五边形的内角和为 度?3.从n边形的一个顶点出发,可以引 条对角线?它们将n边形分成 个三角形?n边形的内角和等于 度?综上所述,你能得到多边形内角和公式吗? 设多边形的边数为n,则n边形的内角和等于______________。 4.多边形的外角及外角和:如图,在六边形的 每个顶点处各取一个外角,这些外角的和叫做六边形的外角和,六边形的外角和等于多少度? (1)任何一个外角同它相邻的内角有什么关系?六边形的6个外角加上与它们相邻的内角,所得的和是多少?上述总和与六边形的内角和、外角和有什么关系?,六边形 的外角和怎样求?如果换成n边形,可以得到同样的结果吗? 由此得出:多边形的外角和等于 。三、巩固新知——(秀出最棒的自已!)1.一个多边形的每一个外角都等于30°,则这个多边形为 边形。一个多边形的每个内角都等于135°,则这个多边形为 边形。 2. 边形的内角和为1440°, 边形的内角和等于外角和的3倍。内角和等于外角和的多边形是 边形。3.四边形的∠A、∠B、∠C、∠D的外角之比为1:2:3:4,那么∠A:∠B:∠C:∠D= 。四、自我反思:———(善于总结是学习的最好方法) 本节课你有哪些收获?(知识上和方法上总结)五、课后提升———(提升自已,让自已与众不同)1.当一个多边形的边数增加时,其外角和( )A.增加 B.减少 C.不变 D.不能确定2.一个十边形的内角和等于( )A. B. C. D.3.正多边形每一个外角都等于,则从此多边形一个顶点出发可引的对角线的条数是( )A.5条 B.6条 C.7条 D.8条4.一个多边形的内角和为900°,则这个多边形是( )A.七边形 B.八边形 C.九边形 D.十边形5.如图,AD是△ABC的高,BE是△ABC的角平分线,BE,AD相交于点F,已知∠BAD=42°,则∠BFD=( )A.45° B.54° C.56° D.66°6.一个正多边形,它的一个内角恰好是一个外角的4倍,则这个正多边形的边数是___________.7.一个多边形的内角和是四边形的内角和的2倍,并且这个多边形的各个内角都相等,这个多边形每个外角等于______.8.正五边形每个内角的度数是_______.9.求出图形中的x值10.若一个多边形的内角和的比一个四边形的内角和多90°,那么这个多边形的边数是多少?11.【感知】如图①,在四边形AEFC中,EB、FD分别是边AE、CF的延长线,我们把∠BEF、∠DFE称为四边形AEFC的外角,若∠A+∠C=260°,则∠BEF+∠DFE= 度.【探究】如图②,在四边形AECF中,EB、FD分别是边AE、AF的延长线,我们把∠BEC、∠DFC称为四边形AECF的外角,试探究∠A、∠C与∠BEC、∠DFC之间的数量关系.【结论】综合以上,请你用文字描述上述关系: .【应用】如图③,FM、EM分别是四边形AEFC的外角∠DFE、∠BEF的平分线,若∠A+∠C=210°,求∠M的度数.参考答案:1.C2.C3.C4.A5.D6.107.60°##60度8.9.3010.[感知]260;[探究]∠A+∠C=∠BEC+∠DFC;[结论]四边形的任意两个外角的和等于与它们不相邻的两个内角的和;[应用]75°
A
B
C
D
E
F
1
2
3
4
5
6
3 / 3
学 习目 标 1.能记住多边形的内角和、外角和的概念。2.能通过不同方法推导多边形的内角和与外角和公式,进一步体会数学化归思想。3.能熟练运用多边形的内角和与外角和公式进行有关计算
学 习方 法 合作交流、讨论
一、自主学习——(相信自已,一定行!)1.我们知道三角形的内角和为__________。2.我们还知道,正方形的四个角都等于____。,那么它的内角和为_____。,同样长方形的内角和也是_______。 3.正方形和长方形都是特殊的四边形,其内角和为360°,那么一般的四边形的内角和为多少呢?二、合作交流——(集体的智慧是无穷的,携手解决下面的问题吧!)1.从四边形的一个顶点出发可以引 条对角线?它们将四边形分成 个三角形?那么四边 形的内角和等于 度?你是怎么得到的?刚才我们是以某一个顶点来分割原图形成若干个三角形,还能在其它地方取点采取同样的方法吗?2.从五边形一个顶点出发可以引 条对角线?它们将五边形分成 个三角形?那么这五边形的内角和为 度?3.从n边形的一个顶点出发,可以引 条对角线?它们将n边形分成 个三角形?n边形的内角和等于 度?综上所述,你能得到多边形内角和公式吗? 设多边形的边数为n,则n边形的内角和等于______________。 4.多边形的外角及外角和:如图,在六边形的 每个顶点处各取一个外角,这些外角的和叫做六边形的外角和,六边形的外角和等于多少度? (1)任何一个外角同它相邻的内角有什么关系?六边形的6个外角加上与它们相邻的内角,所得的和是多少?上述总和与六边形的内角和、外角和有什么关系?,六边形 的外角和怎样求?如果换成n边形,可以得到同样的结果吗? 由此得出:多边形的外角和等于 。三、巩固新知——(秀出最棒的自已!)1.一个多边形的每一个外角都等于30°,则这个多边形为 边形。一个多边形的每个内角都等于135°,则这个多边形为 边形。 2. 边形的内角和为1440°, 边形的内角和等于外角和的3倍。内角和等于外角和的多边形是 边形。3.四边形的∠A、∠B、∠C、∠D的外角之比为1:2:3:4,那么∠A:∠B:∠C:∠D= 。四、自我反思:———(善于总结是学习的最好方法) 本节课你有哪些收获?(知识上和方法上总结)五、课后提升———(提升自已,让自已与众不同)1.当一个多边形的边数增加时,其外角和( )A.增加 B.减少 C.不变 D.不能确定2.一个十边形的内角和等于( )A. B. C. D.3.正多边形每一个外角都等于,则从此多边形一个顶点出发可引的对角线的条数是( )A.5条 B.6条 C.7条 D.8条4.一个多边形的内角和为900°,则这个多边形是( )A.七边形 B.八边形 C.九边形 D.十边形5.如图,AD是△ABC的高,BE是△ABC的角平分线,BE,AD相交于点F,已知∠BAD=42°,则∠BFD=( )A.45° B.54° C.56° D.66°6.一个正多边形,它的一个内角恰好是一个外角的4倍,则这个正多边形的边数是___________.7.一个多边形的内角和是四边形的内角和的2倍,并且这个多边形的各个内角都相等,这个多边形每个外角等于______.8.正五边形每个内角的度数是_______.9.求出图形中的x值10.若一个多边形的内角和的比一个四边形的内角和多90°,那么这个多边形的边数是多少?11.【感知】如图①,在四边形AEFC中,EB、FD分别是边AE、CF的延长线,我们把∠BEF、∠DFE称为四边形AEFC的外角,若∠A+∠C=260°,则∠BEF+∠DFE= 度.【探究】如图②,在四边形AECF中,EB、FD分别是边AE、AF的延长线,我们把∠BEC、∠DFC称为四边形AECF的外角,试探究∠A、∠C与∠BEC、∠DFC之间的数量关系.【结论】综合以上,请你用文字描述上述关系: .【应用】如图③,FM、EM分别是四边形AEFC的外角∠DFE、∠BEF的平分线,若∠A+∠C=210°,求∠M的度数.参考答案:1.C2.C3.C4.A5.D6.107.60°##60度8.9.3010.[感知]260;[探究]∠A+∠C=∠BEC+∠DFC;[结论]四边形的任意两个外角的和等于与它们不相邻的两个内角的和;[应用]75°
A
B
C
D
E
F
1
2
3
4
5
6
3 / 3
