1.5.1 第1课时 有理数的乘法 课件(共29张ppt)
文档属性
| 名称 | 1.5.1 第1课时 有理数的乘法 课件(共29张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 07:12:52 | ||
图片预览







文档简介
(共29张PPT)
1.5 有理数的乘法和除法
1.5.1 有理数的乘法
第1课时 有理数的乘法
湘教版七年级上册
教学目标
1.掌握有理数的乘法法则并能进行熟练地运算.
(重点)
2.掌握多个有理数相乘的积的符号法则.(难点)
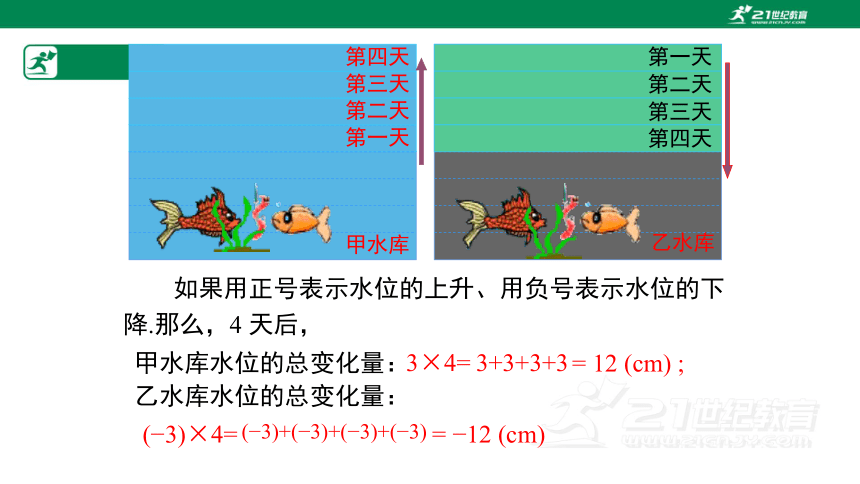
甲水库
第一天
乙水库
第二天
第三天
第四天
第一天
第二天
第三天
第四天
问题1 如图,甲水库的水位每天升高3cm ,乙水库的水位每天下降 3cm ,4 天后,甲、乙水库水位的总变化量是多少?
导入新课
情境引入
甲水库
第一天
乙水库
第二天
第三天
第四天
第一天
第二天
第三天
第四天
如果用正号表示水位的上升、用负号表示水位的下降.那么,4 天后,
甲水库水位的总变化量:
乙水库水位的总变化量:
3+3+3+3
3×4=
= 12 (cm) ;
( 3)×4=
= 12 (cm)
( 3)+( 3)+( 3)+( 3)
( 3)×4=( 3)+( 3)+( 3)+( 3) = 12
( 3)×3 = _____________=_____,
( 3)×2 =_____________=_____,
( 3)×1 =_____,
( 3)×0 =_____.
9
6
3
0
类比前面得到的两个式子,填空:
( 3)+( 3)+( 3)
( 3)+( 3)
3×4=3+3+3+3 = 12
问题2 观看下面视频,你能算出李大爷的餐馆九月份的亏损情况吗?
思考 若两个有理数相乘,其中有负数时,该怎么办?
如图,一只蜗牛沿直线 l爬行,它现在的位置在l上的点O.
l
O
1.如果一只蜗牛向右爬行2cm记为+2cm,那么向左爬行2cm应该记为 .
2.如果3分钟以后记为+3分钟,那么3分钟以前应该记为 .
-2cm
-3分钟
讲授新课
有理数的乘法运算
一
合作探究
探究1
2
O
2
6
4
l
结果:3分钟后在l上点O 边 cm处
表示: .
右
6
(+2)×(+3)= 6
(1)如果蜗牛一直以每分钟2cm的速度向右爬行,3分钟后它在什么位置?
规定:向左为负,向右为正.
现在前为负,现在后为正.
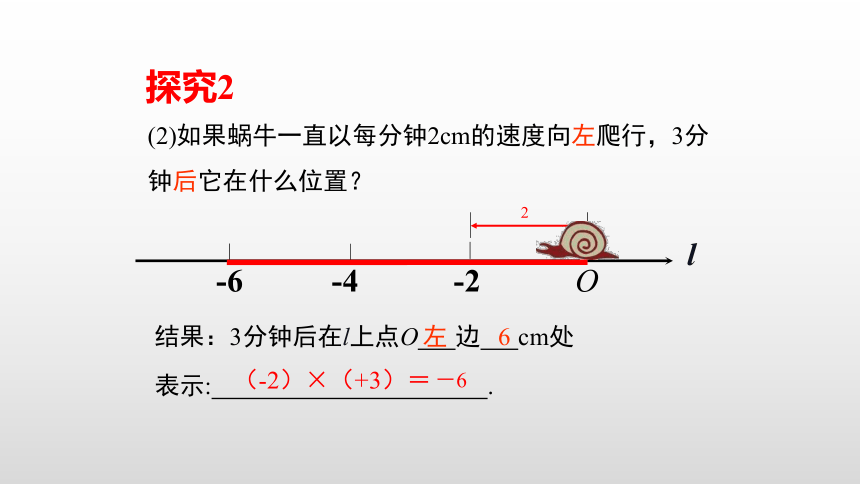
(2)如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟后它在什么位置?
探究2
-6
-4
O
-2
2
l
结果:3分钟后在l上点O 边 cm处
左
6
表示: .
(-2)×(+3)=
-6
2 × 3 = 6
(-2)× 3 = -6
一个因数换成相反数
积是原来的积的相反数
发现:两数相乘,把一个因数换成它的相反数,所得的积是原来积的相反数.
议一议
2 × 3 = 6
2×( -3) =
-6
(-2) ×(-3)=
6
相反数
相反数
相反数
相反数
猜一猜
(3)如果蜗牛一直以每分钟2cm的速度向右爬行,3分钟前它在什么位置?
探究3
2
-6
-4
O
-2
2
l
结果:3分钟前在l上点O 边 cm处
表示: .
(+2)×(-3)=
-6
左
6
验证了前面猜想
(4)如果蜗牛一直以每分钟2 cm的速度向左爬行,3分钟前它在什么位置?
探究4
2
O
2
6
4
-2
l
结果:3钟分前在l上点O 边 cm处.
右
6
表示: .
(-2)×(-3)=
+6
分组讨论:
(1) 2×3 = 6
(2)(-2)×(-3)= 6
(3)(-2) × 3 = -6
(4) 2×(-3) = -6
正数×正数
负数×负数
负数×正数
=正数
=正数
=负数
=负数
正数×负数
发现:两数相乘,同号得正,异号得负,并把绝对值相乘.
结果:都是仍在原处,即结果都是 .
若用式子表达:
探究5
(5)原地不动或运动了零次,结果是什么?
0×3=0;0×(-3)=0;
2×0=0;(-2)×0=0.
零
O
发现:任何数与0相乘,积仍为0.
两数相乘,综合如下:
(1) 2×3 = 6
(2)(-2)×(-3)= 6
(3)(-2) × 3 = -6
(4) 2×(-3) = -6
(5) 3×0= 0,
0×3 = 0
(6)(-3)×0 = 0,
0×(-2)= 0
同号相乘,积为正数
异号相乘,积为负数
如果有一个因数是0时,所得的积还是0.
两数的 符号特征 积的符号 积的绝对值
同 号
异 号 一个因数 为 0 有理数乘法法则:
+
-
绝对值相乘
得 0
先定符号,再定绝对值!
归纳总结
讨论:
(1)若a<0,b>0,则ab____0 ;
(2)若a<0,b<0,则ab____0 ;
(3)若ab>0,则a、b应满足什么条件?
(4)若ab<0,则a、b应满足什么条件?
<
>
a、b同号
a、b异号
先确定下列积的符号,再计算结果:
(1) 5×(-3)
(2)(-4)×6
(3)(-7)×(-9)
(4) 0.5×0.7
积的符号为负
积的符号为负
积的符号为正
积的符号为正
= -15
= -24
= 63
=0.35
做一做
例1 计算:
(1) 3.5×(-2);
(2)
(3)
(4) (-0.57)×0.
解:(1) 3.5×(-2)=-(3.5×2)=-7;
(4) (-0.57)×0=0.
总结:有理数乘法的求解步骤:先确定积的符号;再确定积的绝对值.
例2 用正负数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km,气温的变化量为-6℃,攀登3km后,气温有什么变化?
解:(-6)×3=-18
答:气温下降18℃.
有理数的乘法的应用
二
【变式】气象观测统计资料表明,在一般情况下,高度每上升1km,气温下降6℃.已知甲地现在地面气温为21℃,求甲地上空9km处的气温大约是多少.
解:(-6)×9=-54(℃);
21+(-54)=-33(℃).
答:甲地上空9km处的气温大约为-33℃.
被乘数 乘数 积的符号 积的绝对值 结果
-5 7
15 6
-30 -6
4 -25
1.填空:
-
35
-35
+
90
90
+
180
180
-
100
-100
当堂练习
2. 若 ab>0,则必有 ( )
A. a>0,b>0 B. a<0,b<0
C. a>0,b<0 D. a>0,b>0或a<0,b<0
3.若ab=0,则一定有( )
a=b=0 B. a,b至少有一个为0
C. a=0 D. a,b最多有一个为0
D
B
解:
4.计算:
5.商店降价销售某种商品,每件降5元,售出60件后,与按原价销售同样数量的商品相比,销售额有什么变化?
解:(-5)×60=-300(元)
答:销售额减少300元.
课堂小结
有理数乘法法则
一般法则
应用
两数相乘,同号得正,异号得负,并把绝对值相乘.
特殊
任何数同0相乘,都得0.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.5 有理数的乘法和除法
1.5.1 有理数的乘法
第1课时 有理数的乘法
湘教版七年级上册
教学目标
1.掌握有理数的乘法法则并能进行熟练地运算.
(重点)
2.掌握多个有理数相乘的积的符号法则.(难点)
甲水库
第一天
乙水库
第二天
第三天
第四天
第一天
第二天
第三天
第四天
问题1 如图,甲水库的水位每天升高3cm ,乙水库的水位每天下降 3cm ,4 天后,甲、乙水库水位的总变化量是多少?
导入新课
情境引入
甲水库
第一天
乙水库
第二天
第三天
第四天
第一天
第二天
第三天
第四天
如果用正号表示水位的上升、用负号表示水位的下降.那么,4 天后,
甲水库水位的总变化量:
乙水库水位的总变化量:
3+3+3+3
3×4=
= 12 (cm) ;
( 3)×4=
= 12 (cm)
( 3)+( 3)+( 3)+( 3)
( 3)×4=( 3)+( 3)+( 3)+( 3) = 12
( 3)×3 = _____________=_____,
( 3)×2 =_____________=_____,
( 3)×1 =_____,
( 3)×0 =_____.
9
6
3
0
类比前面得到的两个式子,填空:
( 3)+( 3)+( 3)
( 3)+( 3)
3×4=3+3+3+3 = 12
问题2 观看下面视频,你能算出李大爷的餐馆九月份的亏损情况吗?
思考 若两个有理数相乘,其中有负数时,该怎么办?
如图,一只蜗牛沿直线 l爬行,它现在的位置在l上的点O.
l
O
1.如果一只蜗牛向右爬行2cm记为+2cm,那么向左爬行2cm应该记为 .
2.如果3分钟以后记为+3分钟,那么3分钟以前应该记为 .
-2cm
-3分钟
讲授新课
有理数的乘法运算
一
合作探究
探究1
2
O
2
6
4
l
结果:3分钟后在l上点O 边 cm处
表示: .
右
6
(+2)×(+3)= 6
(1)如果蜗牛一直以每分钟2cm的速度向右爬行,3分钟后它在什么位置?
规定:向左为负,向右为正.
现在前为负,现在后为正.
(2)如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟后它在什么位置?
探究2
-6
-4
O
-2
2
l
结果:3分钟后在l上点O 边 cm处
左
6
表示: .
(-2)×(+3)=
-6
2 × 3 = 6
(-2)× 3 = -6
一个因数换成相反数
积是原来的积的相反数
发现:两数相乘,把一个因数换成它的相反数,所得的积是原来积的相反数.
议一议
2 × 3 = 6
2×( -3) =
-6
(-2) ×(-3)=
6
相反数
相反数
相反数
相反数
猜一猜
(3)如果蜗牛一直以每分钟2cm的速度向右爬行,3分钟前它在什么位置?
探究3
2
-6
-4
O
-2
2
l
结果:3分钟前在l上点O 边 cm处
表示: .
(+2)×(-3)=
-6
左
6
验证了前面猜想
(4)如果蜗牛一直以每分钟2 cm的速度向左爬行,3分钟前它在什么位置?
探究4
2
O
2
6
4
-2
l
结果:3钟分前在l上点O 边 cm处.
右
6
表示: .
(-2)×(-3)=
+6
分组讨论:
(1) 2×3 = 6
(2)(-2)×(-3)= 6
(3)(-2) × 3 = -6
(4) 2×(-3) = -6
正数×正数
负数×负数
负数×正数
=正数
=正数
=负数
=负数
正数×负数
发现:两数相乘,同号得正,异号得负,并把绝对值相乘.
结果:都是仍在原处,即结果都是 .
若用式子表达:
探究5
(5)原地不动或运动了零次,结果是什么?
0×3=0;0×(-3)=0;
2×0=0;(-2)×0=0.
零
O
发现:任何数与0相乘,积仍为0.
两数相乘,综合如下:
(1) 2×3 = 6
(2)(-2)×(-3)= 6
(3)(-2) × 3 = -6
(4) 2×(-3) = -6
(5) 3×0= 0,
0×3 = 0
(6)(-3)×0 = 0,
0×(-2)= 0
同号相乘,积为正数
异号相乘,积为负数
如果有一个因数是0时,所得的积还是0.
两数的 符号特征 积的符号 积的绝对值
同 号
异 号 一个因数 为 0 有理数乘法法则:
+
-
绝对值相乘
得 0
先定符号,再定绝对值!
归纳总结
讨论:
(1)若a<0,b>0,则ab____0 ;
(2)若a<0,b<0,则ab____0 ;
(3)若ab>0,则a、b应满足什么条件?
(4)若ab<0,则a、b应满足什么条件?
<
>
a、b同号
a、b异号
先确定下列积的符号,再计算结果:
(1) 5×(-3)
(2)(-4)×6
(3)(-7)×(-9)
(4) 0.5×0.7
积的符号为负
积的符号为负
积的符号为正
积的符号为正
= -15
= -24
= 63
=0.35
做一做
例1 计算:
(1) 3.5×(-2);
(2)
(3)
(4) (-0.57)×0.
解:(1) 3.5×(-2)=-(3.5×2)=-7;
(4) (-0.57)×0=0.
总结:有理数乘法的求解步骤:先确定积的符号;再确定积的绝对值.
例2 用正负数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km,气温的变化量为-6℃,攀登3km后,气温有什么变化?
解:(-6)×3=-18
答:气温下降18℃.
有理数的乘法的应用
二
【变式】气象观测统计资料表明,在一般情况下,高度每上升1km,气温下降6℃.已知甲地现在地面气温为21℃,求甲地上空9km处的气温大约是多少.
解:(-6)×9=-54(℃);
21+(-54)=-33(℃).
答:甲地上空9km处的气温大约为-33℃.
被乘数 乘数 积的符号 积的绝对值 结果
-5 7
15 6
-30 -6
4 -25
1.填空:
-
35
-35
+
90
90
+
180
180
-
100
-100
当堂练习
2. 若 ab>0,则必有 ( )
A. a>0,b>0 B. a<0,b<0
C. a>0,b<0 D. a>0,b>0或a<0,b<0
3.若ab=0,则一定有( )
a=b=0 B. a,b至少有一个为0
C. a=0 D. a,b最多有一个为0
D
B
解:
4.计算:
5.商店降价销售某种商品,每件降5元,售出60件后,与按原价销售同样数量的商品相比,销售额有什么变化?
解:(-5)×60=-300(元)
答:销售额减少300元.
课堂小结
有理数乘法法则
一般法则
应用
两数相乘,同号得正,异号得负,并把绝对值相乘.
特殊
任何数同0相乘,都得0.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
