北师大版九年级数学上册1.1菱形的性质与判定 综合复习测评 (含答案)
文档属性
| 名称 | 北师大版九年级数学上册1.1菱形的性质与判定 综合复习测评 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 462.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 15:02:21 | ||
图片预览


文档简介
2022-2023学年北师大版九年级数学上册《1.1菱形的性质与判定》
期中综合复习测评(附答案)
一.选择题(共9小题,满分27分)
1.平行四边形ABCD的对角线AC与BD相交于点O,添加以下条件,不能判定平行四边形ABCD为菱形的是( )
A.AC⊥BD B.∠ABD=∠CBD C.AB=BC D.AC=BD
2.已知菱形的两条对角线的长分别为6cm和8cm,则这个菱形的面积是( )
A.20cm2 B.24cm2 C.48cm2 D.100cm2
3.从菱形的钝角顶点,向对角的两边条垂线,垂足恰好在该边的中点,则菱形的内角中钝角的度数是( )
A.150° B.135° C.120° D.100°
4.如图,菱形ABCD的两条对角线相交于点O,若AC=6,菱形的面积等于12,则菱形ABCD的周长等于( )
A.4 B.2 C. D.4
5.如图,菱形ABCD中,AC交BD于O,DE⊥BC于E,连接OE,若∠ABC=140°,则∠OED的度数为( )
A.15° B.20° C.25° D.30°
6.如图,在菱形ABCD中,AC与BD相交于点O,AB=AC,点E在BC上,且∠CAE=15°,AE与BD相交于F,下列结论不正确的是( )
A.∠EBF=30° B.BE=BF C.FA>EF D.OE⊥BC
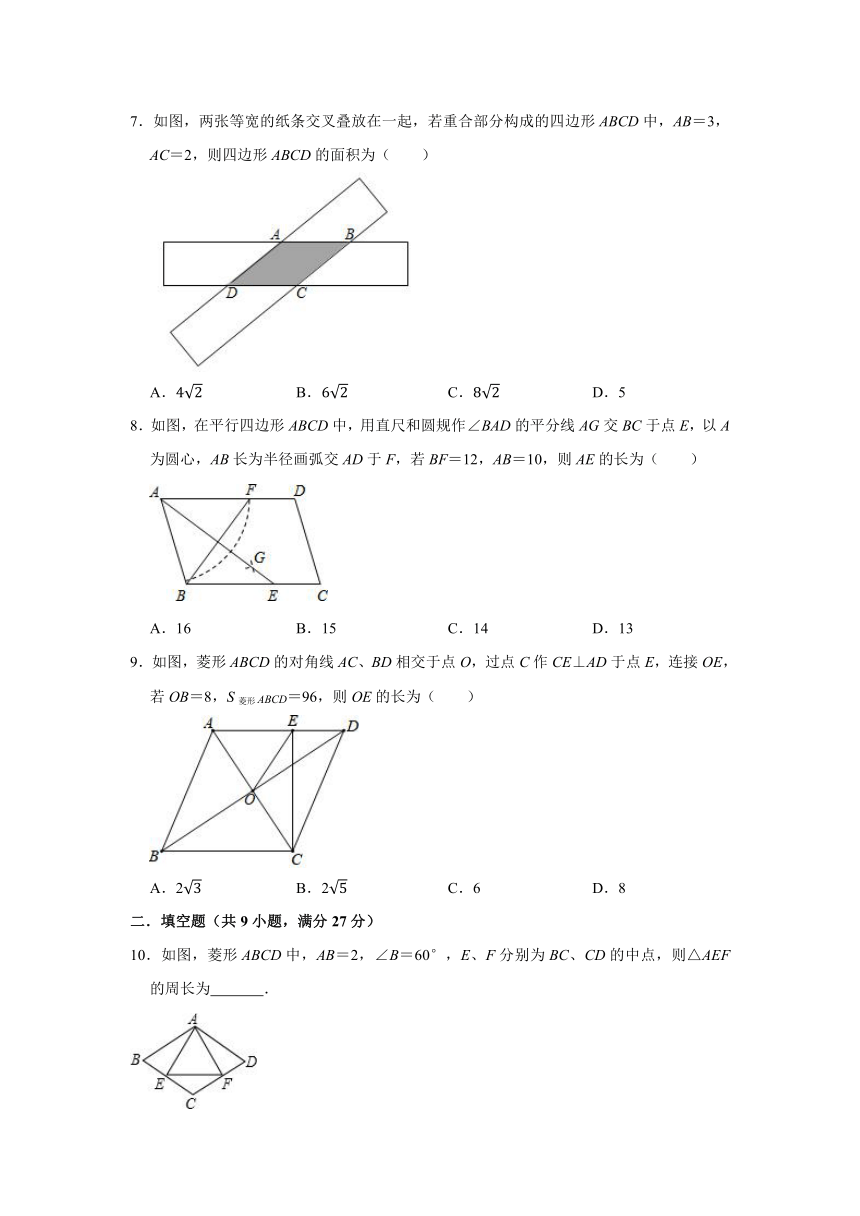
7.如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形ABCD中,AB=3,AC=2,则四边形ABCD的面积为( )
A. B. C. D.5
8.如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB长为半径画弧交AD于F,若BF=12,AB=10,则AE的长为( )
A.16 B.15 C.14 D.13
9.如图,菱形ABCD的对角线AC、BD相交于点O,过点C作CE⊥AD于点E,连接OE,若OB=8,S菱形ABCD=96,则OE的长为( )
A.2 B.2 C.6 D.8
二.填空题(共9小题,满分27分)
10.如图,菱形ABCD中,AB=2,∠B=60°,E、F分别为BC、CD的中点,则△AEF的周长为 .
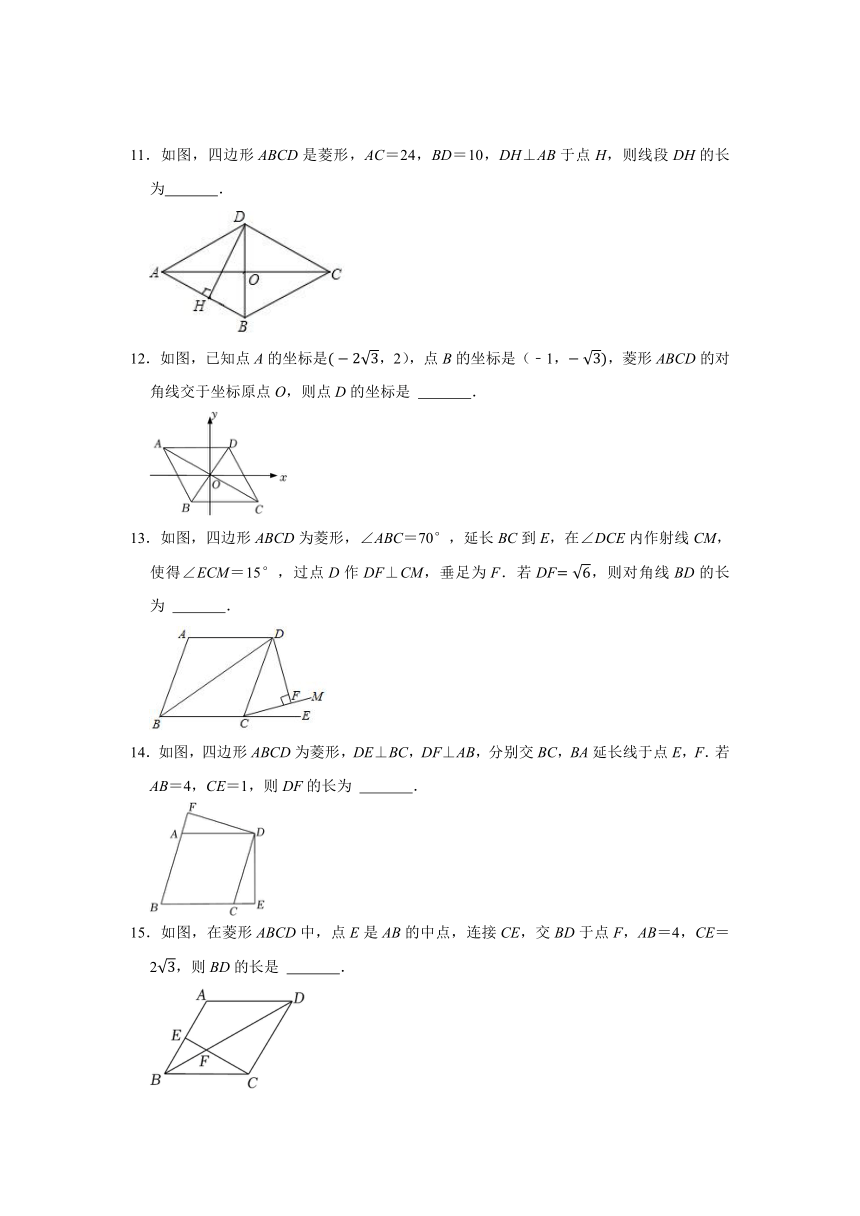
11.如图,四边形ABCD是菱形,AC=24,BD=10,DH⊥AB于点H,则线段DH的长为 .
12.如图,已知点A的坐标是,2),点B的坐标是(﹣1,,菱形ABCD的对角线交于坐标原点O,则点D的坐标是 .
13.如图,四边形ABCD为菱形,∠ABC=70°,延长BC到E,在∠DCE内作射线CM,使得∠ECM=15°,过点D作DF⊥CM,垂足为F.若DF,则对角线BD的长为 .
14.如图,四边形ABCD为菱形,DE⊥BC,DF⊥AB,分别交BC,BA延长线于点E,F.若AB=4,CE=1,则DF的长为 .
15.如图,在菱形ABCD中,点E是AB的中点,连接CE,交BD于点F,AB=4,CE=2,则BD的长是 .
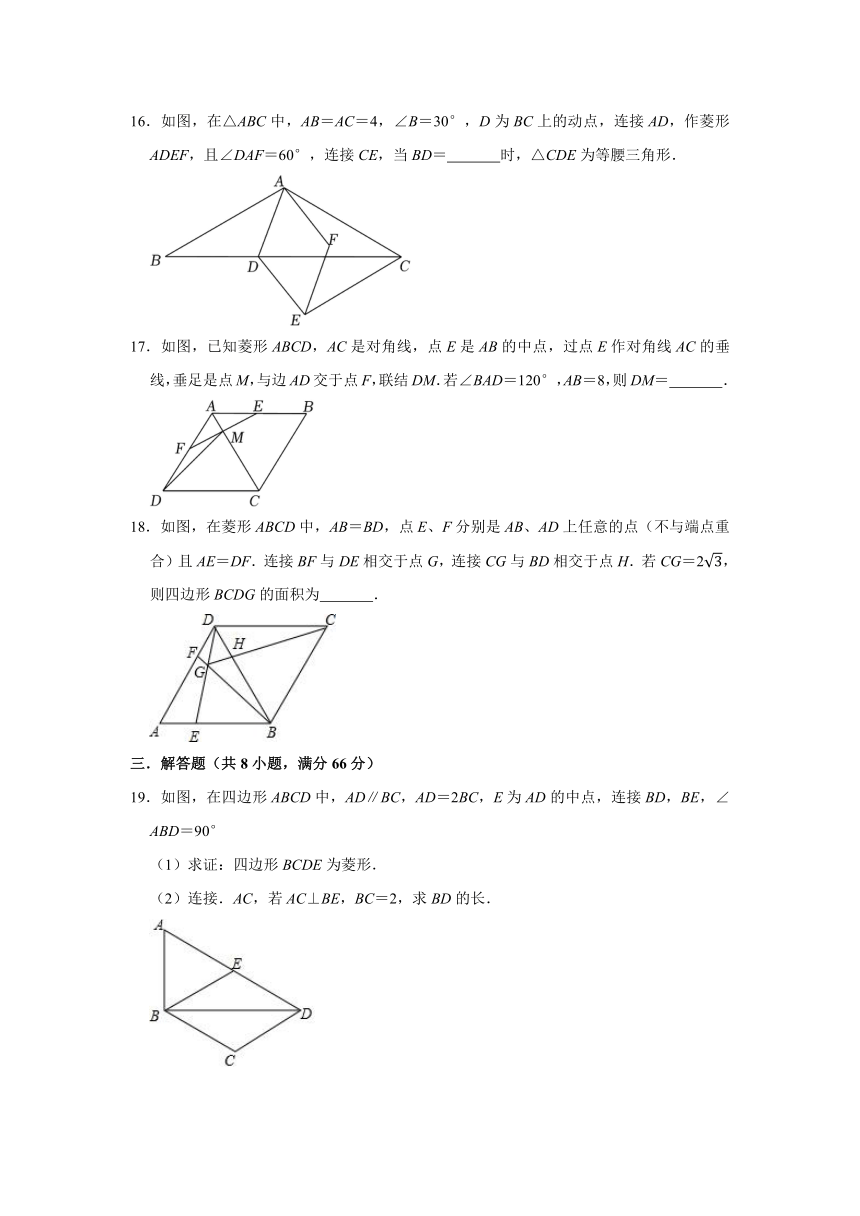
16.如图,在△ABC中,AB=AC=4,∠B=30°,D为BC上的动点,连接AD,作菱形ADEF,且∠DAF=60°,连接CE,当BD= 时,△CDE为等腰三角形.
17.如图,已知菱形ABCD,AC是对角线,点E是AB的中点,过点E作对角线AC的垂线,垂足是点M,与边AD交于点F,联结DM.若∠BAD=120°,AB=8,则DM= .
18.如图,在菱形ABCD中,AB=BD,点E、F分别是AB、AD上任意的点(不与端点重合)且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H.若CG=2,则四边形BCDG的面积为 .
三.解答题(共8小题,满分66分)
19.如图,在四边形ABCD中,AD∥BC,AD=2BC,E为AD的中点,连接BD,BE,∠ABD=90°
(1)求证:四边形BCDE为菱形.
(2)连接.AC,若AC⊥BE,BC=2,求BD的长.
20.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点F,连接OE
(1)求证:四边形ABCD是菱形;
(2)若AB,BD=2,请直接写出△OBE的面积为 .
21.如图,菱形ABCD的周长为8,对角线BD=2,E、F分别是边AD,CD上的两个动点;且满足AE+CF=2.
(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由.
22.已知:如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于点F.
(1)求证:AM=DM;
(2)若DF=3,求菱形ABCD的周长.
23.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且DE=BF,连接AE,CF.
(1)求证:△ADE≌△CBF;
(2)连接AF,CE.当BD与AC满足什么条件时,四边形AFCE是菱形?请说明理由.
24.如图,已知四边形ABCD的对角线AC、BD交于点O,AO=OC,OB=OD且∠1=∠2.
(1)求证:四边形ABCD是菱形;
(2)E为AO上一点,连接BE,若AE=4,AB=6,EB=2,求AO的长.
25.如图,在四边形ABCD中,AD∥BC,对角线BD的垂直平分线与边AD、BC分别相交于点M、N.
(1)求证:四边形BNDM是菱形;
(2)若BD=12,MN=4,求菱形BNDM的周长.
26.如图(1),在菱形ABCD中,E、F分别是边CB,DC上的点,∠B=∠EAF=60°,
(I)求证:∠BAE=∠CEF;
(Ⅱ)如图(2),若点E,F分别移动到边CB,DC的延长线上,其余条件不变,请猜想∠BAE与∠CEF的大小关系,并给予证明.
参考答案
一.选择题(共9小题,满分27分)
1.解:A、∵四边形ABCD是平行四边形,AC⊥BD,
∴平行四边形ABCD是菱形,故选项A不符合题意;
B、∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABD=∠CDB,
又∵∠ABD=∠CBD,
∴∠CDB=∠CBD,
∴BC=DC,
∴平行四边形ABCD是菱形,故选项B不符合题意;
C、∵四边形ABCD是平行四边形,AB=BC,
∴平行四边形ABCD是菱形,故选项C不符合题意;
D、∵四边形ABCD是平行四边形,AC=BD,
∴平行四边形ABCD是矩形,故选项D不符合题意;
故选:D.
2.解:∵菱形的两条对角线的长分别为6cm和8cm,
∴这个菱形的面积6×8=24(cm2),
故选:B.
3.解:过A作AE⊥BC,
由题意知AE⊥BC,且E为BC的中点,
则△ABC为等腰三角形
即AB=AC,即AB=AC=BC,
∴∠ABC=60°,
∴∠BAD=180°﹣∠ABC=180°﹣60°=120°.
故选:C.
4.解:∵菱形的面积等于12,
∴AC BD=12,
∵AC=6,
∴BD=4,
∵菱形ABCD对角线互相垂直平分,
∴BO=OD=2,AO=OC=3,
∴AB,
∴菱形的周长为4.
故选:D.
5.解:∵四边形ABCD是菱形,∠ABC=140°,
∴∠ABD=∠CBD∠ABC=70°,BO=DO,
∵DE⊥BC,
∴OE=OD=OB,∠BDE=20°,
∴∠ODE=∠OED=20°,
故选:B.
6.解:如图在菱形ABCD中,AB=CB=AD=CD,
∵AB=AC,
∴AB=CB=AD=CD=AC,
∴△ABC和△ADC都是等边三角形,
∴∠ABC=∠BAC=∠ACB=60°,
∵BD=BD(公共边)
∴△ABD≌△CBD(SSS),
∴∠ABD=∠CBD∠ABC=30°;
∴∠EBF=30°.
∴A正确;
∵∠ABC=∠BAC=60°,∠CAE=15°,
∴∠BAE=60°﹣15°=45°,
∴∠BEF=180°﹣60°﹣45°=75°,
∴∠BFE=180°﹣30°﹣75°=75°,
∴∠BEF=∠BFE,
∴BE=BF.
∴B正确;
过点F作FG∥BC,交AD于点G,
∵∠GFB=∠FBE=∠GBF,
∴GF=BG,
∴,
∴,
∴,
∵AB=BC>BE,
∴FA>EF,
∴C正确;
假设OE⊥BC正确,则∠BEO=90°,
∵∠BEF=75°,
∴∠OEA=90°﹣75°=15°=∠CAE,
∴OE=OA=OC,
∴∠OEC=∠OCE=60°,
∵∠OEC=60°与OE⊥BC相矛盾,
∴假设不成立,
∴OE⊥BC错误,
∴D不正确.故选:D.
7.解:过点A作AE⊥CD于E,AF⊥BC于F,连接AC,BD交于点O,
∵两条纸条宽度相同,
∴AE=AF.
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
∵S ABCD=BC AF=CD AE.
又∵AE=AF.
∴BC=CD,
∴四边形ABCD是菱形,
∴AO=CO=1,BO=DO,AC⊥BD,
∴BO2,
∴BD=4,
∴四边形ABCD的面积4,
故选:A.
8.解:连接EF,AE与BF交于点O,如图,
∵AO平分∠BAD,
∴∠1=∠2,
∵四边形ABCD为平行四边形,
∴AF∥BE,
∴∠1=∠3,
∴∠2=∠3,
∴AB=EB,
同理:AF=BE,
又∵AF∥BE,
∴四边形ABEF是平行四边形,
∴四边形ABEF是菱形,
∴AE⊥BF,OB=OF=6,OA=OE,
在Rt△AOB中,由勾股定理得:OA8,
∴AE=2OA=16.
故选:A.
9.解:∵四边形ABCD是菱形,
∴OA=OC,OB=ODBD,BD⊥AC,
∴BD=16,
∵S菱形ABCDAC×BD=96,
∴AC=12,
∵CE⊥AD,
∴∠AEC=90°,
∴OEAC=6,
故选:C.
二.填空题(共9小题,满分27分)
10.解:连接AC,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD=2,∠D=∠B=60°,
∴△ABC与△ACD是等边三角形,
∵E、F分别为BC、CD的中点,
∴AE⊥BC,AF⊥CD,
∴AE=AF,∠BAE=∠CAE=∠DAF=∠CAF=30°,
∴∠EAF=60°,
∴AE=AF=EF,
∴△AEF的周长为3.
故答案为3.
11.解:∵四边形ABCD是菱形,AC=24,BD=10,
∴S菱形ABCDAC×BD=120,AO=12,OD=5,AC⊥BD,
∴AD=AB13,
∵DH⊥AB,
∴AO×BD=DH×AB,
∴12×10=13×DH,
∴DH.
故答案为:.
12.解:∵四边形ABCD为菱形,
∴OB=OD,
又∵点O为坐标原点,
∴点B和点D关于原点对称,
∵点B的坐标为(﹣1,),
∴D点坐标为(1,),
故答案为:(1,).
13.解:如图,连接AC交BD于点H,
∵四边形ABCD是菱形,∠ABC=70°,
∴BH=DH,AC⊥BD,CB=CD,∠CBD∠ABC=35°,AB∥CD,
∴∠DHC=90°,∠CDB=∠CBD=35°,∠DCE=∠ABC=70°,
∵∠ECM=15°,
∴∠DCF=∠DCB﹣∠ECM=70°﹣15°=55°,
∵DF⊥CM,
∴∠DFC=90°,
∴∠CDF=90°﹣∠DCF=35°,
∴∠CDH=∠CDF,
在△CDH和△CDF中,
,
∴△CDH≌△CDF(AAS),
∴DH=DF,
∴BD=2DH=2,
故答案为:2.
14.解:∵四边形ABCD为菱形,
∴AB=AD=CD=4,∠DAB=∠DCB,
∴∠DAF=∠DCE,
∵DE⊥BC,DF⊥AB,
∴∠F=∠E=90°,
在△ADF和△CDE中,
,
∴△ADF≌△CDE(AAS),
∴AF=CE=1,
∴DF.
故答案为:.
15.解:∵四边形ABCD是菱形,
∴BC=AB=4.
∵E是AB的中点,
∴BE.
∵BE2+EC216,BC2=42=16,
∴BE2+EC2=BC2.
∴∠BEC=90°.
即CE⊥AB.
连接AC,AC与BD交与点O,如图,
∵四边形ABCD是菱形,
∴AO⊥BD,BO=ODBD,AOAC.
∴∠ABC=60°.
∴△ABC为等边三角形.
∴AC=4.
∴AO=2.
∴BO2.
∴BD=2BO=4.
故答案为:4.
16.解:如图,过点A作AG⊥BC于点G,过点E作EH⊥BC于点H,过点D作DK⊥AB于点K,
在Rt△ABG中,∠AGB=90°,∠B=30°,AB=4,
∴AGAB=2,
∴BG2,
∵AB=AC,AG⊥BC,
∴BC=2BG=4,∠BAG=∠CAG∠BAC,
∵AB=AC,∠B=30°,
∴∠C=∠B=30°,
∴∠BAC=120°,
∴∠BAG=∠CAG=60°,
∵四边形ADEF是菱形,且∠DAF=60°,
∴AD=DE,
设BD=x,则CD=4x,DG=2x,
∴AD2=AG2+DG2=22+(2x)2=x2﹣4x+16,
∴DE2=x2﹣4x+16,
在Rt△BDK中,∠B=30°,
∴DKBDx,
∴BKx,
∴AK=AB﹣BK=4x,
∵∠DAF=60°,
∴∠EDH+∠ADG=120°,
∵∠ADG+∠DAG=90°,∠DAK+∠DAG=∠BAG=60°,
∴∠ADG=∠DAK+30°,
∴∠EDH+∠DAK=90°,
∵∠ADK+∠DAK=90°,
∴∠EDH=∠ADK,
在△EDH和△ADK中,
,
∴△EDH≌△ADK(AAS),
∴EH=AK=4x,DH=DKx,
∴CH=CD﹣DH=4xx=4x,
在Rt△CEH中,CE2=CH2+EH2=(4x)2+(4x)2=3x2﹣16x+64,
∵△CDE为等腰三角形,
∴CD2=CE2或CD2=DE2或CE2=DE2,
当CD2=CE2时,(4x)2=3x2﹣16x+64,
解得:x=22或x=22,
∴BD=22或22;
当CD2=DE2时,(4x)2=x2﹣4x+16,
解得:x,
∴BD,DC,
此时点在点G的右侧,DG=BD﹣BG2,
∴tan∠ADG,
∴∠ADG=60°,
∴∠ADC=120°,
∵四边形ADEF是菱形,且∠DAF=60°,
∴DE=AD,且∠ADE=∠ADC=120°
即点E与点C重合,△CDE不存在,
∴BD不符合题意,舍去;
当CE2=DE2时,3x2﹣16x+64=x2﹣4x+16,
化简得:x2﹣6x+24=0,
解得:x=2或x=4,
当x=4,即BD=4时,点D与点C重合,△CDE不存在,故舍去,
∴BD=2.
综上所述,BD=22或22或或2时,△CDE为等腰三角形.
故答案为:22或22或2.
17.解:过M作MN⊥AD于N,
∵四边形ABCD是菱形,AB=8,
∴∠DAC=∠BAC∠BAD120°=60°,
∵EF⊥AC,
∴AE=AF=4,∠AFM=30°,
∴AM=2,
Rt△AMN中,∠AMN=30°,
∴AN=1,MN,
∵AD=AB=2AE=8,
∴DN=8﹣1=7,
由勾股定理得:DM,
故答案为:2.
18.解:如图,过点C作CM⊥GB于M,CN⊥GD于N,则∠CMG=∠CNG=90°,
∵四边形ABCD为菱形,
∴AB=AD.
又∵AB=BD,
∴△ABD为等边三角形.
∴∠A=∠BDF=60°.
又∵AE=DF,AD=BD,
∴△AED≌△DFB(SAS),
∴∠ADE=∠DBF,
∴∠BGE=∠BDG+∠DBG=∠BDG+∠ADE=60°,
∴∠BGD=120°,
又∵菱形ABCD中,∠BCD=∠A=60°,
∴∠BGD+∠BCD=180°,
∴∠CBM+∠CDG=180°,
又∵∠CDN+∠CDG=180°,
∴∠CDN=∠CBM,
又∵CD=CB,∠CMB=∠CNG=90°,
∴△CBM≌△CDN(AAS),
∴CN=CM,
又∵CM⊥GB,CN⊥GD,
∴CG平分∠BGD,
∴∠MGC=60°,
∵△CBM≌△CDN,
∴S四边形BCDG=S四边形CMGN,
∵CG=CG,CM=CN,∠CMG=∠CNG=90°,
∴△CMG≌△CNG(HL),
∴S四边形CMGN=2S△CMG,
∵∠CGM=60°,CM⊥GM,
∴∠GCM=30°,
∴GMCG,CMCG=3,
∴S四边形BCDG=S四边形CMGN=2S△CMG=23=3.
故答案为:.
三.解答题(共8小题,满分66分)
19.(1)证明:∵∠ABD=90°,E是AD的中点,
∴BE=DE=AE,
∵AD=2BC,
∴BC=DE,
∵AD∥BC,
∴四边形BCDE为平行四边形,
∵BE=DE,
∴四边形BCDE为菱形;
(2)解:由(1)得:四边形BCDE为菱形,
∴BC=BE,
∵AD∥BC,
∴四边形ABCE为平行四边形,
∵AC⊥BE,
∴四边形ABCE为菱形,
∴BC=AB=2,AD=2BC=4,
∵∠ABD=90°,
∴BD.
20.(1)证明:∵AB∥CD,
∴∠CAB=∠DCA,
∵AC为∠BAD的平分线,
∴∠CAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD,
∵AB=AD,
∴AB=CD,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AB=AD,
∴平行四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,OBBD=1,
∴∠AOB=90°,
∴OA3,
∴AC=2OA=6,
∵CE⊥AB,
∴∠AEC=90°=∠AOB,
又∵∠OAB=∠EAC,
∴:EA,
∴BE=EA﹣AB,
过O作OP⊥AE于P,
则OP,
∴△OBE的面积,
故答案为:.
21.(1)证明:∵菱形ABCD的边长为2,对角线BD=2,
∴AB=AD=BD=2,BC=CD=BD=2,
∴△ABD与△BCD都是等边三角形,
∴∠BDE=∠C=60°,
∵AE+CF=2,
∴CF=2﹣AE,
又∵DE=AD﹣AE=2﹣AE,
∴DE=CF,
在△BDE和△BCF中,
,
∴△BDE≌△BCF(SAS);
(2)解:△BEF是等边三角形.理由如下:
由(1)可知△BDE≌△BCF,
∴BE=BF,∠DBE=∠CBF,
∴∠EBF=∠DBE+∠DBF=∠CBF+∠DBF=∠DBC=60°,
∴△BEF是等边三角形.
22.(1)证明:连接BD,如图所示:
∵四边形ABCD是菱形,
∴BD⊥AC,AB∥CD,
∵EF⊥AC,
∴EF∥BD,
∴四边形EFDB是平行四边形,
∴DF=EB,
∵E是AB中点,
∴AE=EB,
∴AE=DF,
∵AB∥CD,
∴∠EAM=∠ADF,
在△AEM和△DMF中,
,
∴△AME≌△DMF(AAS),
∴AM=DM;
(2)解:由(1)知△AME≌△DMF,
∴AE=DF=3,
.∵E为AB的中点,
∴AB=2AE=6,
∴菱形ABCD的周长为6×4=24.
23.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADB=∠CBD,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS);
(2)解:当AC⊥BD时,四边形AFCE是菱形,理由如下:
∵四边形ABCD是平行四边形,
∴OB=OD,
∴AC⊥BD,
∵△ADE≌△CBF,
∴AE=CF,∠AED=∠CFB,
∴AE∥CF,
∴四边形AFCE是平行四边形,
∵AC⊥BD,
∴ AFCE是菱形.
24.(1)证明:∵AO=OC,OB=OD,
∴四边形ABCD是平行四边形,
∴AD∥BC,
∴∠2=∠ACB,
∵∠1=∠2,
∴∠1=∠ACB
∴AB=CB,
∴平行四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴AC⊥BD,
在Rt△ABO和Rt△EBO中,根据勾股定理得:OB2=AB2﹣AO2=BE2﹣OE2,
设OE=x,
∵AE=4,AB=6,EB=2,AO=4+x,
∴62﹣(4+x)2=(2)2﹣x2,
解得:x=1,
∴AO=AE+OE=4+1=5.
25.(1)证明:∵AD∥BC,
∴∠DMO=∠BNO,
∵MN是对角线BD的垂直平分线,
∴OB=OD,MN⊥BD,
在△MOD和△NOB中,
,
∴△MOD≌△NOB(AAS),
∴OM=ON,
∵OB=OD,
∴四边形BNDM是平行四边形,
∵MN⊥BD,
∴平行四边形BNDM是菱形;
(2)解:由(1)可知,OB=OBD=6,OM=ONMN=2,四边形BNDM是菱形,
∴BN=DN=DM=BM,
∵MN⊥BD,
∴∠BON=90°,
∴BN2,
∴菱形BNDM的周长=4BN=8.
26.(I)证明:在图(1)中,连接AC.
∵四边形ABCD是菱形,
∴AB=BC,AB∥CD,CA平分∠BCD.
∵∠B=60°,
∴△ABC是等边三角形,
∴∠B=∠BAC=60°,AB=AC.
∵AB∥CD,
∴∠ACD=∠BAC=60°,
∴∠B=∠ACD=60°.
∵∠EAF=60°,
∴∠BAE+∠EAC=∠EAC+∠CAF=60°,
∴∠BAE=∠CAF.
在△ABE和△ACF中,,
∴△ABE≌△ACF(ASA),
∴AE=AF,
∴△AEF为等边三角形,
∴∠AEF=60°,
∴∠CEF+∠AEB=120°.
∵∠BAE+∠AEB=120°,
∴∠BAE=∠CEF.
(II)解:∠BAE=∠CEF.
在图(2)中,连接AC,由(I)知:∠ABC=∠ACD=60°,∠EAF=∠BAC=60°,AB=AC,
∴∠ABE=∠ACF=120°,∠BAE=∠CAF.
在△ABE和△ACF中,,
∴△ABE≌△ACF(AAS),
∴AE=AF,
∴△AEF为等边三角形,
∴∠AEF=60°,
∴∠AEB+∠CEF=60°.
∵∠AEB+∠BAE=∠ABC=60°,
∴∠BAE=∠CEF.
期中综合复习测评(附答案)
一.选择题(共9小题,满分27分)
1.平行四边形ABCD的对角线AC与BD相交于点O,添加以下条件,不能判定平行四边形ABCD为菱形的是( )
A.AC⊥BD B.∠ABD=∠CBD C.AB=BC D.AC=BD
2.已知菱形的两条对角线的长分别为6cm和8cm,则这个菱形的面积是( )
A.20cm2 B.24cm2 C.48cm2 D.100cm2
3.从菱形的钝角顶点,向对角的两边条垂线,垂足恰好在该边的中点,则菱形的内角中钝角的度数是( )
A.150° B.135° C.120° D.100°
4.如图,菱形ABCD的两条对角线相交于点O,若AC=6,菱形的面积等于12,则菱形ABCD的周长等于( )
A.4 B.2 C. D.4
5.如图,菱形ABCD中,AC交BD于O,DE⊥BC于E,连接OE,若∠ABC=140°,则∠OED的度数为( )
A.15° B.20° C.25° D.30°
6.如图,在菱形ABCD中,AC与BD相交于点O,AB=AC,点E在BC上,且∠CAE=15°,AE与BD相交于F,下列结论不正确的是( )
A.∠EBF=30° B.BE=BF C.FA>EF D.OE⊥BC
7.如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形ABCD中,AB=3,AC=2,则四边形ABCD的面积为( )
A. B. C. D.5
8.如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB长为半径画弧交AD于F,若BF=12,AB=10,则AE的长为( )
A.16 B.15 C.14 D.13
9.如图,菱形ABCD的对角线AC、BD相交于点O,过点C作CE⊥AD于点E,连接OE,若OB=8,S菱形ABCD=96,则OE的长为( )
A.2 B.2 C.6 D.8
二.填空题(共9小题,满分27分)
10.如图,菱形ABCD中,AB=2,∠B=60°,E、F分别为BC、CD的中点,则△AEF的周长为 .
11.如图,四边形ABCD是菱形,AC=24,BD=10,DH⊥AB于点H,则线段DH的长为 .
12.如图,已知点A的坐标是,2),点B的坐标是(﹣1,,菱形ABCD的对角线交于坐标原点O,则点D的坐标是 .
13.如图,四边形ABCD为菱形,∠ABC=70°,延长BC到E,在∠DCE内作射线CM,使得∠ECM=15°,过点D作DF⊥CM,垂足为F.若DF,则对角线BD的长为 .
14.如图,四边形ABCD为菱形,DE⊥BC,DF⊥AB,分别交BC,BA延长线于点E,F.若AB=4,CE=1,则DF的长为 .
15.如图,在菱形ABCD中,点E是AB的中点,连接CE,交BD于点F,AB=4,CE=2,则BD的长是 .
16.如图,在△ABC中,AB=AC=4,∠B=30°,D为BC上的动点,连接AD,作菱形ADEF,且∠DAF=60°,连接CE,当BD= 时,△CDE为等腰三角形.
17.如图,已知菱形ABCD,AC是对角线,点E是AB的中点,过点E作对角线AC的垂线,垂足是点M,与边AD交于点F,联结DM.若∠BAD=120°,AB=8,则DM= .
18.如图,在菱形ABCD中,AB=BD,点E、F分别是AB、AD上任意的点(不与端点重合)且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H.若CG=2,则四边形BCDG的面积为 .
三.解答题(共8小题,满分66分)
19.如图,在四边形ABCD中,AD∥BC,AD=2BC,E为AD的中点,连接BD,BE,∠ABD=90°
(1)求证:四边形BCDE为菱形.
(2)连接.AC,若AC⊥BE,BC=2,求BD的长.
20.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点F,连接OE
(1)求证:四边形ABCD是菱形;
(2)若AB,BD=2,请直接写出△OBE的面积为 .
21.如图,菱形ABCD的周长为8,对角线BD=2,E、F分别是边AD,CD上的两个动点;且满足AE+CF=2.
(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由.
22.已知:如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于点F.
(1)求证:AM=DM;
(2)若DF=3,求菱形ABCD的周长.
23.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且DE=BF,连接AE,CF.
(1)求证:△ADE≌△CBF;
(2)连接AF,CE.当BD与AC满足什么条件时,四边形AFCE是菱形?请说明理由.
24.如图,已知四边形ABCD的对角线AC、BD交于点O,AO=OC,OB=OD且∠1=∠2.
(1)求证:四边形ABCD是菱形;
(2)E为AO上一点,连接BE,若AE=4,AB=6,EB=2,求AO的长.
25.如图,在四边形ABCD中,AD∥BC,对角线BD的垂直平分线与边AD、BC分别相交于点M、N.
(1)求证:四边形BNDM是菱形;
(2)若BD=12,MN=4,求菱形BNDM的周长.
26.如图(1),在菱形ABCD中,E、F分别是边CB,DC上的点,∠B=∠EAF=60°,
(I)求证:∠BAE=∠CEF;
(Ⅱ)如图(2),若点E,F分别移动到边CB,DC的延长线上,其余条件不变,请猜想∠BAE与∠CEF的大小关系,并给予证明.
参考答案
一.选择题(共9小题,满分27分)
1.解:A、∵四边形ABCD是平行四边形,AC⊥BD,
∴平行四边形ABCD是菱形,故选项A不符合题意;
B、∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABD=∠CDB,
又∵∠ABD=∠CBD,
∴∠CDB=∠CBD,
∴BC=DC,
∴平行四边形ABCD是菱形,故选项B不符合题意;
C、∵四边形ABCD是平行四边形,AB=BC,
∴平行四边形ABCD是菱形,故选项C不符合题意;
D、∵四边形ABCD是平行四边形,AC=BD,
∴平行四边形ABCD是矩形,故选项D不符合题意;
故选:D.
2.解:∵菱形的两条对角线的长分别为6cm和8cm,
∴这个菱形的面积6×8=24(cm2),
故选:B.
3.解:过A作AE⊥BC,
由题意知AE⊥BC,且E为BC的中点,
则△ABC为等腰三角形
即AB=AC,即AB=AC=BC,
∴∠ABC=60°,
∴∠BAD=180°﹣∠ABC=180°﹣60°=120°.
故选:C.
4.解:∵菱形的面积等于12,
∴AC BD=12,
∵AC=6,
∴BD=4,
∵菱形ABCD对角线互相垂直平分,
∴BO=OD=2,AO=OC=3,
∴AB,
∴菱形的周长为4.
故选:D.
5.解:∵四边形ABCD是菱形,∠ABC=140°,
∴∠ABD=∠CBD∠ABC=70°,BO=DO,
∵DE⊥BC,
∴OE=OD=OB,∠BDE=20°,
∴∠ODE=∠OED=20°,
故选:B.
6.解:如图在菱形ABCD中,AB=CB=AD=CD,
∵AB=AC,
∴AB=CB=AD=CD=AC,
∴△ABC和△ADC都是等边三角形,
∴∠ABC=∠BAC=∠ACB=60°,
∵BD=BD(公共边)
∴△ABD≌△CBD(SSS),
∴∠ABD=∠CBD∠ABC=30°;
∴∠EBF=30°.
∴A正确;
∵∠ABC=∠BAC=60°,∠CAE=15°,
∴∠BAE=60°﹣15°=45°,
∴∠BEF=180°﹣60°﹣45°=75°,
∴∠BFE=180°﹣30°﹣75°=75°,
∴∠BEF=∠BFE,
∴BE=BF.
∴B正确;
过点F作FG∥BC,交AD于点G,
∵∠GFB=∠FBE=∠GBF,
∴GF=BG,
∴,
∴,
∴,
∵AB=BC>BE,
∴FA>EF,
∴C正确;
假设OE⊥BC正确,则∠BEO=90°,
∵∠BEF=75°,
∴∠OEA=90°﹣75°=15°=∠CAE,
∴OE=OA=OC,
∴∠OEC=∠OCE=60°,
∵∠OEC=60°与OE⊥BC相矛盾,
∴假设不成立,
∴OE⊥BC错误,
∴D不正确.故选:D.
7.解:过点A作AE⊥CD于E,AF⊥BC于F,连接AC,BD交于点O,
∵两条纸条宽度相同,
∴AE=AF.
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
∵S ABCD=BC AF=CD AE.
又∵AE=AF.
∴BC=CD,
∴四边形ABCD是菱形,
∴AO=CO=1,BO=DO,AC⊥BD,
∴BO2,
∴BD=4,
∴四边形ABCD的面积4,
故选:A.
8.解:连接EF,AE与BF交于点O,如图,
∵AO平分∠BAD,
∴∠1=∠2,
∵四边形ABCD为平行四边形,
∴AF∥BE,
∴∠1=∠3,
∴∠2=∠3,
∴AB=EB,
同理:AF=BE,
又∵AF∥BE,
∴四边形ABEF是平行四边形,
∴四边形ABEF是菱形,
∴AE⊥BF,OB=OF=6,OA=OE,
在Rt△AOB中,由勾股定理得:OA8,
∴AE=2OA=16.
故选:A.
9.解:∵四边形ABCD是菱形,
∴OA=OC,OB=ODBD,BD⊥AC,
∴BD=16,
∵S菱形ABCDAC×BD=96,
∴AC=12,
∵CE⊥AD,
∴∠AEC=90°,
∴OEAC=6,
故选:C.
二.填空题(共9小题,满分27分)
10.解:连接AC,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD=2,∠D=∠B=60°,
∴△ABC与△ACD是等边三角形,
∵E、F分别为BC、CD的中点,
∴AE⊥BC,AF⊥CD,
∴AE=AF,∠BAE=∠CAE=∠DAF=∠CAF=30°,
∴∠EAF=60°,
∴AE=AF=EF,
∴△AEF的周长为3.
故答案为3.
11.解:∵四边形ABCD是菱形,AC=24,BD=10,
∴S菱形ABCDAC×BD=120,AO=12,OD=5,AC⊥BD,
∴AD=AB13,
∵DH⊥AB,
∴AO×BD=DH×AB,
∴12×10=13×DH,
∴DH.
故答案为:.
12.解:∵四边形ABCD为菱形,
∴OB=OD,
又∵点O为坐标原点,
∴点B和点D关于原点对称,
∵点B的坐标为(﹣1,),
∴D点坐标为(1,),
故答案为:(1,).
13.解:如图,连接AC交BD于点H,
∵四边形ABCD是菱形,∠ABC=70°,
∴BH=DH,AC⊥BD,CB=CD,∠CBD∠ABC=35°,AB∥CD,
∴∠DHC=90°,∠CDB=∠CBD=35°,∠DCE=∠ABC=70°,
∵∠ECM=15°,
∴∠DCF=∠DCB﹣∠ECM=70°﹣15°=55°,
∵DF⊥CM,
∴∠DFC=90°,
∴∠CDF=90°﹣∠DCF=35°,
∴∠CDH=∠CDF,
在△CDH和△CDF中,
,
∴△CDH≌△CDF(AAS),
∴DH=DF,
∴BD=2DH=2,
故答案为:2.
14.解:∵四边形ABCD为菱形,
∴AB=AD=CD=4,∠DAB=∠DCB,
∴∠DAF=∠DCE,
∵DE⊥BC,DF⊥AB,
∴∠F=∠E=90°,
在△ADF和△CDE中,
,
∴△ADF≌△CDE(AAS),
∴AF=CE=1,
∴DF.
故答案为:.
15.解:∵四边形ABCD是菱形,
∴BC=AB=4.
∵E是AB的中点,
∴BE.
∵BE2+EC216,BC2=42=16,
∴BE2+EC2=BC2.
∴∠BEC=90°.
即CE⊥AB.
连接AC,AC与BD交与点O,如图,
∵四边形ABCD是菱形,
∴AO⊥BD,BO=ODBD,AOAC.
∴∠ABC=60°.
∴△ABC为等边三角形.
∴AC=4.
∴AO=2.
∴BO2.
∴BD=2BO=4.
故答案为:4.
16.解:如图,过点A作AG⊥BC于点G,过点E作EH⊥BC于点H,过点D作DK⊥AB于点K,
在Rt△ABG中,∠AGB=90°,∠B=30°,AB=4,
∴AGAB=2,
∴BG2,
∵AB=AC,AG⊥BC,
∴BC=2BG=4,∠BAG=∠CAG∠BAC,
∵AB=AC,∠B=30°,
∴∠C=∠B=30°,
∴∠BAC=120°,
∴∠BAG=∠CAG=60°,
∵四边形ADEF是菱形,且∠DAF=60°,
∴AD=DE,
设BD=x,则CD=4x,DG=2x,
∴AD2=AG2+DG2=22+(2x)2=x2﹣4x+16,
∴DE2=x2﹣4x+16,
在Rt△BDK中,∠B=30°,
∴DKBDx,
∴BKx,
∴AK=AB﹣BK=4x,
∵∠DAF=60°,
∴∠EDH+∠ADG=120°,
∵∠ADG+∠DAG=90°,∠DAK+∠DAG=∠BAG=60°,
∴∠ADG=∠DAK+30°,
∴∠EDH+∠DAK=90°,
∵∠ADK+∠DAK=90°,
∴∠EDH=∠ADK,
在△EDH和△ADK中,
,
∴△EDH≌△ADK(AAS),
∴EH=AK=4x,DH=DKx,
∴CH=CD﹣DH=4xx=4x,
在Rt△CEH中,CE2=CH2+EH2=(4x)2+(4x)2=3x2﹣16x+64,
∵△CDE为等腰三角形,
∴CD2=CE2或CD2=DE2或CE2=DE2,
当CD2=CE2时,(4x)2=3x2﹣16x+64,
解得:x=22或x=22,
∴BD=22或22;
当CD2=DE2时,(4x)2=x2﹣4x+16,
解得:x,
∴BD,DC,
此时点在点G的右侧,DG=BD﹣BG2,
∴tan∠ADG,
∴∠ADG=60°,
∴∠ADC=120°,
∵四边形ADEF是菱形,且∠DAF=60°,
∴DE=AD,且∠ADE=∠ADC=120°
即点E与点C重合,△CDE不存在,
∴BD不符合题意,舍去;
当CE2=DE2时,3x2﹣16x+64=x2﹣4x+16,
化简得:x2﹣6x+24=0,
解得:x=2或x=4,
当x=4,即BD=4时,点D与点C重合,△CDE不存在,故舍去,
∴BD=2.
综上所述,BD=22或22或或2时,△CDE为等腰三角形.
故答案为:22或22或2.
17.解:过M作MN⊥AD于N,
∵四边形ABCD是菱形,AB=8,
∴∠DAC=∠BAC∠BAD120°=60°,
∵EF⊥AC,
∴AE=AF=4,∠AFM=30°,
∴AM=2,
Rt△AMN中,∠AMN=30°,
∴AN=1,MN,
∵AD=AB=2AE=8,
∴DN=8﹣1=7,
由勾股定理得:DM,
故答案为:2.
18.解:如图,过点C作CM⊥GB于M,CN⊥GD于N,则∠CMG=∠CNG=90°,
∵四边形ABCD为菱形,
∴AB=AD.
又∵AB=BD,
∴△ABD为等边三角形.
∴∠A=∠BDF=60°.
又∵AE=DF,AD=BD,
∴△AED≌△DFB(SAS),
∴∠ADE=∠DBF,
∴∠BGE=∠BDG+∠DBG=∠BDG+∠ADE=60°,
∴∠BGD=120°,
又∵菱形ABCD中,∠BCD=∠A=60°,
∴∠BGD+∠BCD=180°,
∴∠CBM+∠CDG=180°,
又∵∠CDN+∠CDG=180°,
∴∠CDN=∠CBM,
又∵CD=CB,∠CMB=∠CNG=90°,
∴△CBM≌△CDN(AAS),
∴CN=CM,
又∵CM⊥GB,CN⊥GD,
∴CG平分∠BGD,
∴∠MGC=60°,
∵△CBM≌△CDN,
∴S四边形BCDG=S四边形CMGN,
∵CG=CG,CM=CN,∠CMG=∠CNG=90°,
∴△CMG≌△CNG(HL),
∴S四边形CMGN=2S△CMG,
∵∠CGM=60°,CM⊥GM,
∴∠GCM=30°,
∴GMCG,CMCG=3,
∴S四边形BCDG=S四边形CMGN=2S△CMG=23=3.
故答案为:.
三.解答题(共8小题,满分66分)
19.(1)证明:∵∠ABD=90°,E是AD的中点,
∴BE=DE=AE,
∵AD=2BC,
∴BC=DE,
∵AD∥BC,
∴四边形BCDE为平行四边形,
∵BE=DE,
∴四边形BCDE为菱形;
(2)解:由(1)得:四边形BCDE为菱形,
∴BC=BE,
∵AD∥BC,
∴四边形ABCE为平行四边形,
∵AC⊥BE,
∴四边形ABCE为菱形,
∴BC=AB=2,AD=2BC=4,
∵∠ABD=90°,
∴BD.
20.(1)证明:∵AB∥CD,
∴∠CAB=∠DCA,
∵AC为∠BAD的平分线,
∴∠CAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD,
∵AB=AD,
∴AB=CD,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AB=AD,
∴平行四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,OBBD=1,
∴∠AOB=90°,
∴OA3,
∴AC=2OA=6,
∵CE⊥AB,
∴∠AEC=90°=∠AOB,
又∵∠OAB=∠EAC,
∴:EA,
∴BE=EA﹣AB,
过O作OP⊥AE于P,
则OP,
∴△OBE的面积,
故答案为:.
21.(1)证明:∵菱形ABCD的边长为2,对角线BD=2,
∴AB=AD=BD=2,BC=CD=BD=2,
∴△ABD与△BCD都是等边三角形,
∴∠BDE=∠C=60°,
∵AE+CF=2,
∴CF=2﹣AE,
又∵DE=AD﹣AE=2﹣AE,
∴DE=CF,
在△BDE和△BCF中,
,
∴△BDE≌△BCF(SAS);
(2)解:△BEF是等边三角形.理由如下:
由(1)可知△BDE≌△BCF,
∴BE=BF,∠DBE=∠CBF,
∴∠EBF=∠DBE+∠DBF=∠CBF+∠DBF=∠DBC=60°,
∴△BEF是等边三角形.
22.(1)证明:连接BD,如图所示:
∵四边形ABCD是菱形,
∴BD⊥AC,AB∥CD,
∵EF⊥AC,
∴EF∥BD,
∴四边形EFDB是平行四边形,
∴DF=EB,
∵E是AB中点,
∴AE=EB,
∴AE=DF,
∵AB∥CD,
∴∠EAM=∠ADF,
在△AEM和△DMF中,
,
∴△AME≌△DMF(AAS),
∴AM=DM;
(2)解:由(1)知△AME≌△DMF,
∴AE=DF=3,
.∵E为AB的中点,
∴AB=2AE=6,
∴菱形ABCD的周长为6×4=24.
23.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADB=∠CBD,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS);
(2)解:当AC⊥BD时,四边形AFCE是菱形,理由如下:
∵四边形ABCD是平行四边形,
∴OB=OD,
∴AC⊥BD,
∵△ADE≌△CBF,
∴AE=CF,∠AED=∠CFB,
∴AE∥CF,
∴四边形AFCE是平行四边形,
∵AC⊥BD,
∴ AFCE是菱形.
24.(1)证明:∵AO=OC,OB=OD,
∴四边形ABCD是平行四边形,
∴AD∥BC,
∴∠2=∠ACB,
∵∠1=∠2,
∴∠1=∠ACB
∴AB=CB,
∴平行四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴AC⊥BD,
在Rt△ABO和Rt△EBO中,根据勾股定理得:OB2=AB2﹣AO2=BE2﹣OE2,
设OE=x,
∵AE=4,AB=6,EB=2,AO=4+x,
∴62﹣(4+x)2=(2)2﹣x2,
解得:x=1,
∴AO=AE+OE=4+1=5.
25.(1)证明:∵AD∥BC,
∴∠DMO=∠BNO,
∵MN是对角线BD的垂直平分线,
∴OB=OD,MN⊥BD,
在△MOD和△NOB中,
,
∴△MOD≌△NOB(AAS),
∴OM=ON,
∵OB=OD,
∴四边形BNDM是平行四边形,
∵MN⊥BD,
∴平行四边形BNDM是菱形;
(2)解:由(1)可知,OB=OBD=6,OM=ONMN=2,四边形BNDM是菱形,
∴BN=DN=DM=BM,
∵MN⊥BD,
∴∠BON=90°,
∴BN2,
∴菱形BNDM的周长=4BN=8.
26.(I)证明:在图(1)中,连接AC.
∵四边形ABCD是菱形,
∴AB=BC,AB∥CD,CA平分∠BCD.
∵∠B=60°,
∴△ABC是等边三角形,
∴∠B=∠BAC=60°,AB=AC.
∵AB∥CD,
∴∠ACD=∠BAC=60°,
∴∠B=∠ACD=60°.
∵∠EAF=60°,
∴∠BAE+∠EAC=∠EAC+∠CAF=60°,
∴∠BAE=∠CAF.
在△ABE和△ACF中,,
∴△ABE≌△ACF(ASA),
∴AE=AF,
∴△AEF为等边三角形,
∴∠AEF=60°,
∴∠CEF+∠AEB=120°.
∵∠BAE+∠AEB=120°,
∴∠BAE=∠CEF.
(II)解:∠BAE=∠CEF.
在图(2)中,连接AC,由(I)知:∠ABC=∠ACD=60°,∠EAF=∠BAC=60°,AB=AC,
∴∠ABE=∠ACF=120°,∠BAE=∠CAF.
在△ABE和△ACF中,,
∴△ABE≌△ACF(AAS),
∴AE=AF,
∴△AEF为等边三角形,
∴∠AEF=60°,
∴∠AEB+∠CEF=60°.
∵∠AEB+∠BAE=∠ABC=60°,
∴∠BAE=∠CEF.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
