1.5.2 第1课时 有理数的除法 课件(共28页ppt)
文档属性
| 名称 | 1.5.2 第1课时 有理数的除法 课件(共28页ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 08:41:31 | ||
图片预览








文档简介
(共28张PPT)
1.5 有理数的乘法和除法
1.5.2 有理数的除法
第1课时 有理数的除法
湘教版七年级上册
教学目标
1.认识有理数的除法,经历除法的运算过程.
2.理解除法法则,体验除法与乘法的转化关系.
3.掌握有理数的除法及乘除混合运算.(重点、难点)
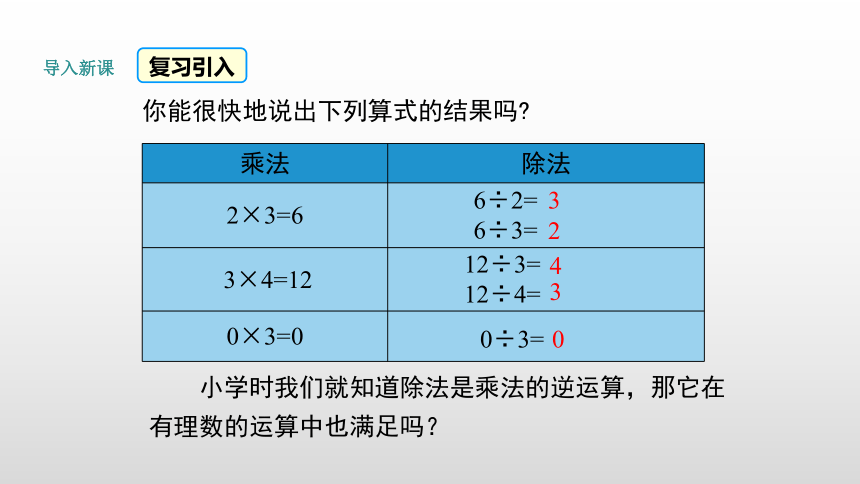
你能很快地说出下列算式的结果吗
小学时我们就知道除法是乘法的逆运算,那它在有理数的运算中也满足吗?
导入新课
复习引入
乘法 除法
2×3=6
3×4=12
0×3=0
0÷3=
12÷3=
12÷4=
6÷2=
6÷3=
3
3
2
4
0
2×(-3)=____ ,
(-4)×(-3)=____,
8×9=____,
0×(-6)=____,
(-4)×3 =____ ,
(-6) ÷2=____,
12÷(-4)=____,
72÷9=____,
(-12)÷(-4)=____,
0÷(-6)=____,
观察右侧算式, 你能发现两个有理数相除时:
商的符号如何确定
商的绝对值如何确定
-6
12
72
-12
0
-3
-3
8
0
3
问题1 对于有理数,除法也是乘法的逆运算,根据这个关系请计算:
讲授新课
有理数的除法
一
(-6) ÷2=____,
12÷(-4)=____,
72÷9=____,
(-12)÷(-4)=____,
0÷(-6)=____,
-3
-3
8
0
异号两数相除得负,
并把绝对值相除
同号两数相除得正,
并把绝对值相除
零除以任何非零数得零
3
1.同号两数相除得正数,异号两数相除得负数,
并把它们的绝对值相除.
2.0除以一个不等于0的数都得0,0不能做除数.
总结归纳
有理数的除法法则1:
(1)(-24)÷4;
(2)(-18)÷(-9);
例1 计算:
解:(2)原式=+(18÷9)=2;
(3)10÷(-5).
解:(3)原式=-( 10 ÷ 5 )=-2.
解:(1)原式=-(24÷4)=-6;
典例精析
(-12)÷( )÷(-100)
下面两种计算正确吗 请说明理由:
(1)解:原式=(-12)÷( ÷100)
=(-12) ÷ =-14400
(2)解:原式=( )÷(-12)÷(-100)
= ÷(-100)=
除法不适合交换律与结合律,所以不正确.
(×)
(×)
想一想
(1)(-15)÷(-3)
(2)12÷(- )
1
4
计算:
解:(2)原式=-(12÷ )=-48
1
4
(3)(-0.75)÷0.25
解:(3)原式=-( 0.75 ÷ 0.25 )=-3
解:(1)原式=+(15÷3)=5
练一练
做一做: 计算:
(1) ×2; (2)(- )×(-2).
解:(1) ×2 = 1
(2)(- )×(-2)= 1
观察上面两题有何特点
结论:
有理数中仍然有:乘积是1的两个数互为倒数.
倒数
二
倒 数 的 定 义
我们把乘积为1的两个有理数称为互为倒数,
其中的一个数是另一个数的倒数.
注意:
1.正数的倒数是正数,负数的倒数是负数;
2.分数的倒数是分子与分母颠倒位置;
3.求小数的倒数,先化成分数,再求倒数;
4.0没有倒数.
知识要点
(1)1的倒数为_____;
(2)-1的倒数为______;
(3) 的倒数为______;
(4) 的倒数为______;
(5) 的倒数为_____;
(6) 的倒数为______.
1
-1
3
-3
思考 a的倒数是 对吗?
不对,a≠0时,a的倒数是 .
练一练
填空:
例2 已知a与b互为相反数,c与d互为倒数,m的绝对值为6,求 -cd+m的值.
解:由题意得a+b=0,cd=1,|m|=6,m=±6;
∴ 当m=6时,原式=0-1+6=5;
当m=-6时,原式=0-1-6=-7.
故 -cd+|m|的值为5.
方法总结:解答此题的关键是先根据题意得出a+b=0,cd=1及m=±6,再代入所求代数式进行计算.
问题 先填空,再对比两边,你能发现什么规律?
观察与发现:
互为倒数
互为倒数
互为倒数
互为倒数
思考 从中你能得出什么结论?
注意:0不能作除数.
有理数的除法法则2:
除以一个不等于零的数等于乘这个数的倒数.
总结归纳
互为倒数
除法变乘法
例3 计算:
典例精析
方法总结:运算中遇到小数和分数时,把小数化成分数,带分数化成假分数,然后相除.
除以一个不等于0的数,等于乘这个数的倒数
有理数除法法则
两数相除,同号得正,异号得负,并把绝对值相除.0除以任何一个不等于0的数,都得0
不能够整除的或是含有分数时选择
能够整除时选择
求两有理数相除如何选择才合适:
总结归纳
例4 已知|a|=5,b=3,且 <0,求a+b的值.
解:因为|a|=5,所以a=±5.
因为b=3, <0,所以a=-5,
所以a+b=-5+3=-2.
方法总结:有理数a,b相除的符号确定:
若 >0,则a>0,b>0或a<0,b<0;
若 =0,则a=0,b≠0;
若 <0,则a>0,b<0或a<0,b>0.
【变式】已知a、b为有理数,且ab>0,求
的值.
解:因为ab>0,
所以a>0,b>0或a<0,b<0.
当a>0,b>0时,
当a<0,b<0时,
-4
-8
0
1. 计算:
当堂练习
2.填空:
(1)若 互为相反数,且 ,则 ________,
________;
(2)当 时, =_______;
(3)若 则 的符号分别是_____________.
3.计算 :
解:
拓展 a,b,c为非零有理数,求 的值.
解:当a<0,b>0,c>0时,
原式= =-1+1+(-1)+(-1)=-2;
当a<0,b<0,c>0时,
原式= =1+(-1)+(-1)+1=0;
当a<0,b<0,c<0时,
原式= =1+1+1+(-1)=2;
当a>0,b>0,c>0时,
原式= =4.
两个有理数相除,同号得正,异号得负,并把绝对值相除.
法则一
法则二
除法
有理数
0除以任何非0的数都得0.
除以一个数等于乘这个数的倒数.
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.5 有理数的乘法和除法
1.5.2 有理数的除法
第1课时 有理数的除法
湘教版七年级上册
教学目标
1.认识有理数的除法,经历除法的运算过程.
2.理解除法法则,体验除法与乘法的转化关系.
3.掌握有理数的除法及乘除混合运算.(重点、难点)
你能很快地说出下列算式的结果吗
小学时我们就知道除法是乘法的逆运算,那它在有理数的运算中也满足吗?
导入新课
复习引入
乘法 除法
2×3=6
3×4=12
0×3=0
0÷3=
12÷3=
12÷4=
6÷2=
6÷3=
3
3
2
4
0
2×(-3)=____ ,
(-4)×(-3)=____,
8×9=____,
0×(-6)=____,
(-4)×3 =____ ,
(-6) ÷2=____,
12÷(-4)=____,
72÷9=____,
(-12)÷(-4)=____,
0÷(-6)=____,
观察右侧算式, 你能发现两个有理数相除时:
商的符号如何确定
商的绝对值如何确定
-6
12
72
-12
0
-3
-3
8
0
3
问题1 对于有理数,除法也是乘法的逆运算,根据这个关系请计算:
讲授新课
有理数的除法
一
(-6) ÷2=____,
12÷(-4)=____,
72÷9=____,
(-12)÷(-4)=____,
0÷(-6)=____,
-3
-3
8
0
异号两数相除得负,
并把绝对值相除
同号两数相除得正,
并把绝对值相除
零除以任何非零数得零
3
1.同号两数相除得正数,异号两数相除得负数,
并把它们的绝对值相除.
2.0除以一个不等于0的数都得0,0不能做除数.
总结归纳
有理数的除法法则1:
(1)(-24)÷4;
(2)(-18)÷(-9);
例1 计算:
解:(2)原式=+(18÷9)=2;
(3)10÷(-5).
解:(3)原式=-( 10 ÷ 5 )=-2.
解:(1)原式=-(24÷4)=-6;
典例精析
(-12)÷( )÷(-100)
下面两种计算正确吗 请说明理由:
(1)解:原式=(-12)÷( ÷100)
=(-12) ÷ =-14400
(2)解:原式=( )÷(-12)÷(-100)
= ÷(-100)=
除法不适合交换律与结合律,所以不正确.
(×)
(×)
想一想
(1)(-15)÷(-3)
(2)12÷(- )
1
4
计算:
解:(2)原式=-(12÷ )=-48
1
4
(3)(-0.75)÷0.25
解:(3)原式=-( 0.75 ÷ 0.25 )=-3
解:(1)原式=+(15÷3)=5
练一练
做一做: 计算:
(1) ×2; (2)(- )×(-2).
解:(1) ×2 = 1
(2)(- )×(-2)= 1
观察上面两题有何特点
结论:
有理数中仍然有:乘积是1的两个数互为倒数.
倒数
二
倒 数 的 定 义
我们把乘积为1的两个有理数称为互为倒数,
其中的一个数是另一个数的倒数.
注意:
1.正数的倒数是正数,负数的倒数是负数;
2.分数的倒数是分子与分母颠倒位置;
3.求小数的倒数,先化成分数,再求倒数;
4.0没有倒数.
知识要点
(1)1的倒数为_____;
(2)-1的倒数为______;
(3) 的倒数为______;
(4) 的倒数为______;
(5) 的倒数为_____;
(6) 的倒数为______.
1
-1
3
-3
思考 a的倒数是 对吗?
不对,a≠0时,a的倒数是 .
练一练
填空:
例2 已知a与b互为相反数,c与d互为倒数,m的绝对值为6,求 -cd+m的值.
解:由题意得a+b=0,cd=1,|m|=6,m=±6;
∴ 当m=6时,原式=0-1+6=5;
当m=-6时,原式=0-1-6=-7.
故 -cd+|m|的值为5.
方法总结:解答此题的关键是先根据题意得出a+b=0,cd=1及m=±6,再代入所求代数式进行计算.
问题 先填空,再对比两边,你能发现什么规律?
观察与发现:
互为倒数
互为倒数
互为倒数
互为倒数
思考 从中你能得出什么结论?
注意:0不能作除数.
有理数的除法法则2:
除以一个不等于零的数等于乘这个数的倒数.
总结归纳
互为倒数
除法变乘法
例3 计算:
典例精析
方法总结:运算中遇到小数和分数时,把小数化成分数,带分数化成假分数,然后相除.
除以一个不等于0的数,等于乘这个数的倒数
有理数除法法则
两数相除,同号得正,异号得负,并把绝对值相除.0除以任何一个不等于0的数,都得0
不能够整除的或是含有分数时选择
能够整除时选择
求两有理数相除如何选择才合适:
总结归纳
例4 已知|a|=5,b=3,且 <0,求a+b的值.
解:因为|a|=5,所以a=±5.
因为b=3, <0,所以a=-5,
所以a+b=-5+3=-2.
方法总结:有理数a,b相除的符号确定:
若 >0,则a>0,b>0或a<0,b<0;
若 =0,则a=0,b≠0;
若 <0,则a>0,b<0或a<0,b>0.
【变式】已知a、b为有理数,且ab>0,求
的值.
解:因为ab>0,
所以a>0,b>0或a<0,b<0.
当a>0,b>0时,
当a<0,b<0时,
-4
-8
0
1. 计算:
当堂练习
2.填空:
(1)若 互为相反数,且 ,则 ________,
________;
(2)当 时, =_______;
(3)若 则 的符号分别是_____________.
3.计算 :
解:
拓展 a,b,c为非零有理数,求 的值.
解:当a<0,b>0,c>0时,
原式= =-1+1+(-1)+(-1)=-2;
当a<0,b<0,c>0时,
原式= =1+(-1)+(-1)+1=0;
当a<0,b<0,c<0时,
原式= =1+1+1+(-1)=2;
当a>0,b>0,c>0时,
原式= =4.
两个有理数相除,同号得正,异号得负,并把绝对值相除.
法则一
法则二
除法
有理数
0除以任何非0的数都得0.
除以一个数等于乘这个数的倒数.
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
