2021-2022学年人教版数学七年级上册1.2.1有理数 课件(共15张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学七年级上册1.2.1有理数 课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 700.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 15:06:27 | ||
图片预览




文档简介
(共15张PPT)
1.2.1有理数
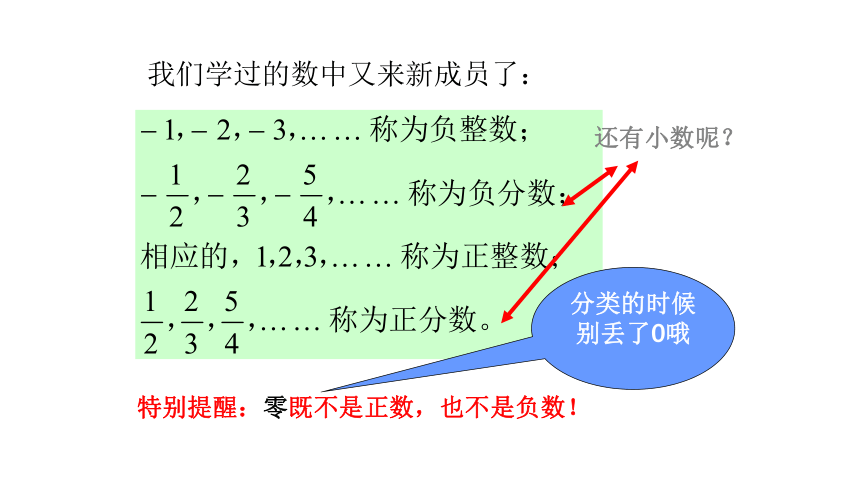
我们学过的数中又来新成员了:
特别提醒:零既不是正数,也不是负数!
分类的时候别丢了0哦
还有小数呢?
( )
整数 ( )
( )
有理数
( )
分数
( )
正整数
0
负整数
正分数
负整数
正整数、零和负整数统称为整数;正分数、负分数统称为分数;整数和分数统称有理数。
特别提醒:零既不是正数,也不是负数!
有理数
正整数
负整数
负分数
正有理数
负有理数
正分数
零
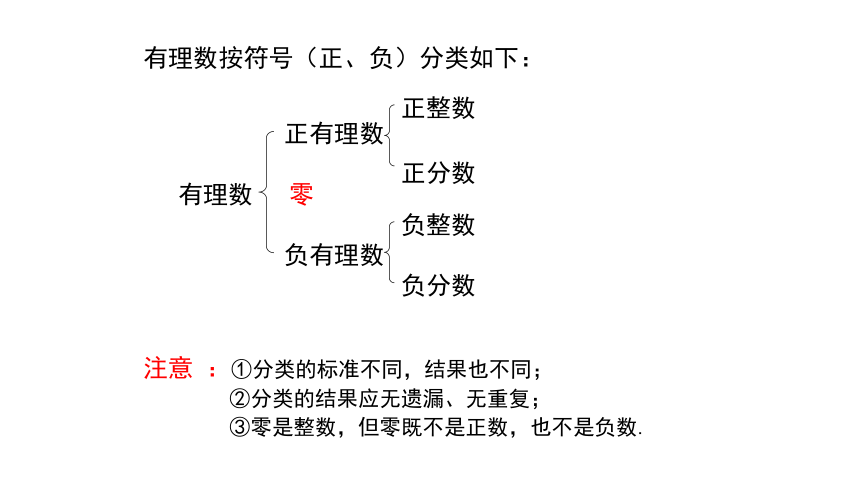
有理数按符号(正、负)分类如下:
注意 :①分类的标准不同,结果也不同;
②分类的结果应无遗漏、无重复;
③零是整数,但零既不是正数,也不是负数.
有理数
正整数
负整数
负分数
正有理数
负有理数
正分数
零
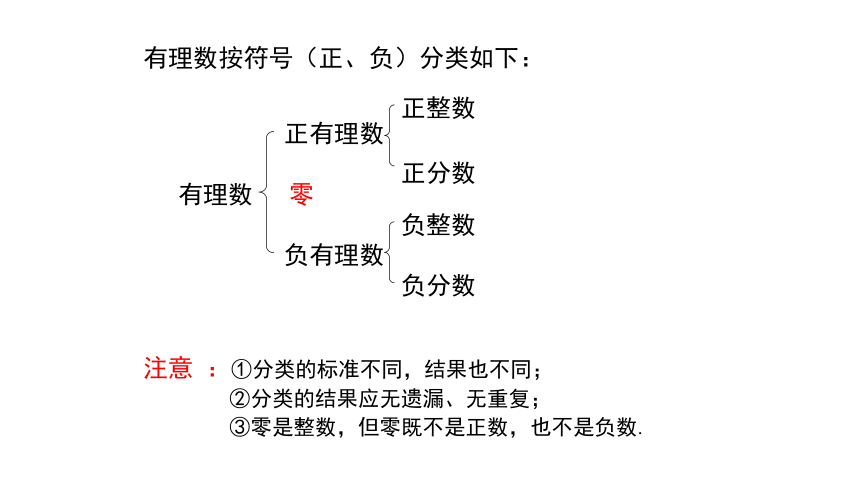
有理数按符号(正、负)分类如下:
注意 :①分类的标准不同,结果也不同;
②分类的结果应无遗漏、无重复;
③零是整数,但零既不是正数,也不是负数.
解:
22 , + , 0.33是正数;
-8.4 , - , -9 是负数;
22 , 0, -9 是整数;
以上所给各数均为有理数.
-8.4 , + , 0.33 , - 是分数;
例 下列给出的各数,哪些是正数?哪些是负数?哪些是整数?哪些是分数?哪些是有理数?
-8.44,22,+ ,0.33,0,- ,-9
我能解决!
2、判断表中各数分别是什么数,在相应的空格内打“√”。
正整数 整数 分数 正数 负数 有理数
2003 √ √ √ √
-4.9
0
-12
√ √ √
√ √ √
√ √
√ √ √
我能解决!
3.小数除有限小数、无限循环小数外,还有一类无限不循环小数(无理数),不在有理数的学习范围(以后学习).所以,我们不能说小数都是有理数.
0
理解概念
2.两个整数的比(如 等)、有限小数(如0.2,-3.14等)、无限循环小数(如 )等都是分数;
1.整数中除了正整数和负整数,还有_____.
几点注意:
2.下列说法错误的有几个?
①负整数和负分数统称为负有理数;
②正整数,0和负整数统称为整数;
③正有理数与负有理数组成全体有理数;
④一个有理数不是正数,就是负数;
⑤一个分数,不是正分数,就是负分数;
⑥最小的正整数是1.
1.下列说法正确的有几个?
①零是整数;②零是有理数;③零是自然数;
④零是正数;⑤零是负数;⑥零是非负数.
巩固概念
4个
2个
1.所有正数组成正数集合,所有负数组成负数集合.把下面的有理数填入它属于的集合的圈内:
2.指出下列各数中的正数、负数、整数、分数:
课堂练习
1.把下列各数填入相应的集合圈里:
巩固练习
(1)0是整数( )
(2)自然数一定是整数( )
(3)0一定是正整数( )
(4)整数一定是自然数( )
√
√
×
×
2、判 断
3、如果用一个字母表示一个数,那a可能是什么样的数?一定是正数吗?
答:不一定,a可能是正数,可能是负数,也可能是0。
探 究
课堂小结
这节课我们的收获:
1、有理数的概念。
2、有理数的分类。
3、数学方法:分类思想。
1.2.1有理数
我们学过的数中又来新成员了:
特别提醒:零既不是正数,也不是负数!
分类的时候别丢了0哦
还有小数呢?
( )
整数 ( )
( )
有理数
( )
分数
( )
正整数
0
负整数
正分数
负整数
正整数、零和负整数统称为整数;正分数、负分数统称为分数;整数和分数统称有理数。
特别提醒:零既不是正数,也不是负数!
有理数
正整数
负整数
负分数
正有理数
负有理数
正分数
零
有理数按符号(正、负)分类如下:
注意 :①分类的标准不同,结果也不同;
②分类的结果应无遗漏、无重复;
③零是整数,但零既不是正数,也不是负数.
有理数
正整数
负整数
负分数
正有理数
负有理数
正分数
零
有理数按符号(正、负)分类如下:
注意 :①分类的标准不同,结果也不同;
②分类的结果应无遗漏、无重复;
③零是整数,但零既不是正数,也不是负数.
解:
22 , + , 0.33是正数;
-8.4 , - , -9 是负数;
22 , 0, -9 是整数;
以上所给各数均为有理数.
-8.4 , + , 0.33 , - 是分数;
例 下列给出的各数,哪些是正数?哪些是负数?哪些是整数?哪些是分数?哪些是有理数?
-8.44,22,+ ,0.33,0,- ,-9
我能解决!
2、判断表中各数分别是什么数,在相应的空格内打“√”。
正整数 整数 分数 正数 负数 有理数
2003 √ √ √ √
-4.9
0
-12
√ √ √
√ √ √
√ √
√ √ √
我能解决!
3.小数除有限小数、无限循环小数外,还有一类无限不循环小数(无理数),不在有理数的学习范围(以后学习).所以,我们不能说小数都是有理数.
0
理解概念
2.两个整数的比(如 等)、有限小数(如0.2,-3.14等)、无限循环小数(如 )等都是分数;
1.整数中除了正整数和负整数,还有_____.
几点注意:
2.下列说法错误的有几个?
①负整数和负分数统称为负有理数;
②正整数,0和负整数统称为整数;
③正有理数与负有理数组成全体有理数;
④一个有理数不是正数,就是负数;
⑤一个分数,不是正分数,就是负分数;
⑥最小的正整数是1.
1.下列说法正确的有几个?
①零是整数;②零是有理数;③零是自然数;
④零是正数;⑤零是负数;⑥零是非负数.
巩固概念
4个
2个
1.所有正数组成正数集合,所有负数组成负数集合.把下面的有理数填入它属于的集合的圈内:
2.指出下列各数中的正数、负数、整数、分数:
课堂练习
1.把下列各数填入相应的集合圈里:
巩固练习
(1)0是整数( )
(2)自然数一定是整数( )
(3)0一定是正整数( )
(4)整数一定是自然数( )
√
√
×
×
2、判 断
3、如果用一个字母表示一个数,那a可能是什么样的数?一定是正数吗?
答:不一定,a可能是正数,可能是负数,也可能是0。
探 究
课堂小结
这节课我们的收获:
1、有理数的概念。
2、有理数的分类。
3、数学方法:分类思想。
