11.1.2 三角形的高、中线与角平分线-11.1.3 三角形的稳定性 习题课件(共18张PPT)
文档属性
| 名称 | 11.1.2 三角形的高、中线与角平分线-11.1.3 三角形的稳定性 习题课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 00:00:00 | ||
图片预览


文档简介
(共18张PPT)
知识构建
例题引路
台知识构建
高
三角形
相关
线段
中线
重心
角平分线
稳定性
例题引路
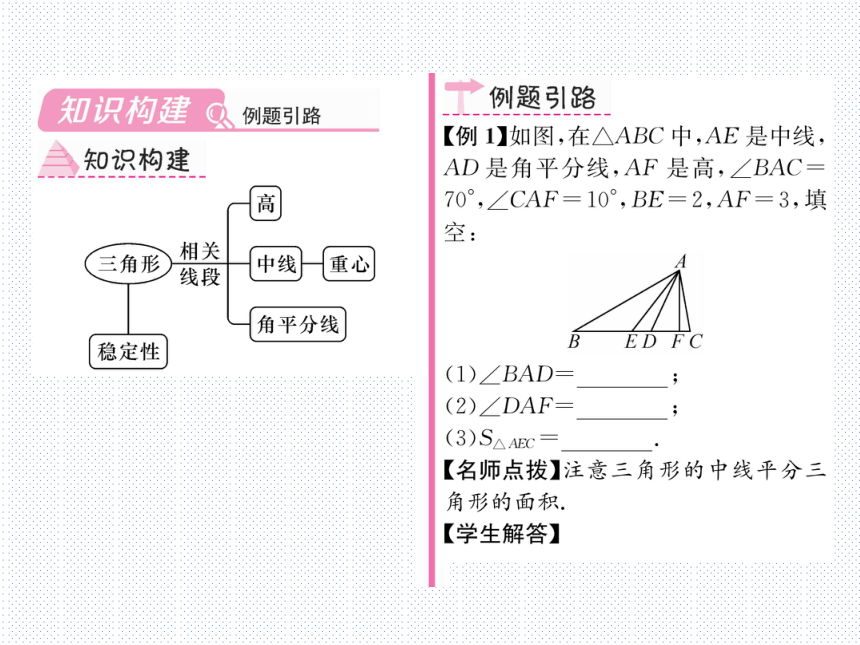
【例1】如图,在△ABC中,AE是中线,
AD是角平分线,AF是高,∠BAC=
70°,∠CAF=10°,BE=2,AF=3,填
空:
B ED FC
(1)∠BAD=
9
(2)∠DAF=
(3)SAAEC=
【名师点拨】注意三角形的中线平分三
角形的面积,
【学生解答】(1)35°;(2)25°;(3)3
【例2】桥梁拉杆、电视机底座都是三角形
结构,这是利用了三角形的
性.
【学生解答】稳定
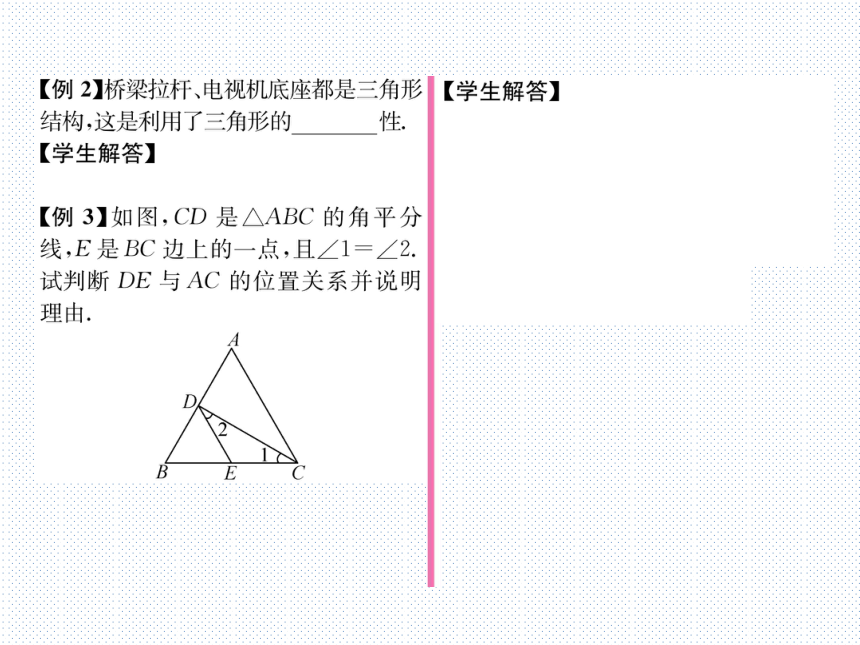
【例3】如图,CD是△ABC的角平分
线,E是BC边上的一点,且∠1=∠2.
试判断DE与AC的位置关系并说明
理由.
B
【学生解答】解:DE∥AC.理由如下:
CD是△ABC的角平分线,
.∠ACD=∠1.
.∠1=∠2,
.∠ACD=∠2,
∴.DE∥AC.
基础过关
逐点击破
知识点①
,三角形的高、中线及角平分线的应用
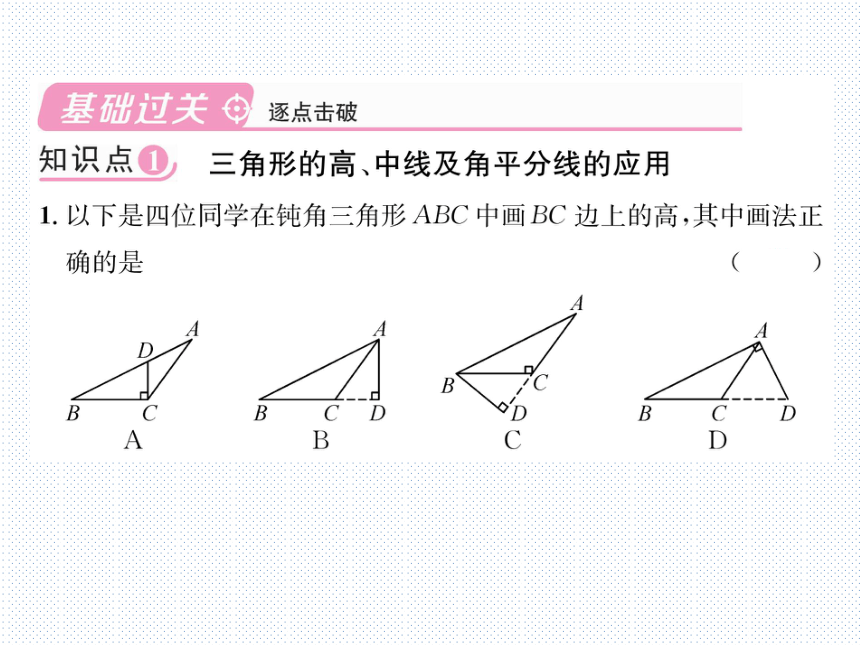
1.以下是四位同学在钝角三角形ABC中画BC边上的高,其中画法正
确的是
(B
B
2.三角形一边上的中线一定把原三角形分成两个
(B
A.形状相同的三角形
B.面积相等的三角形
C.直角三角形
D.周长相等的三角形
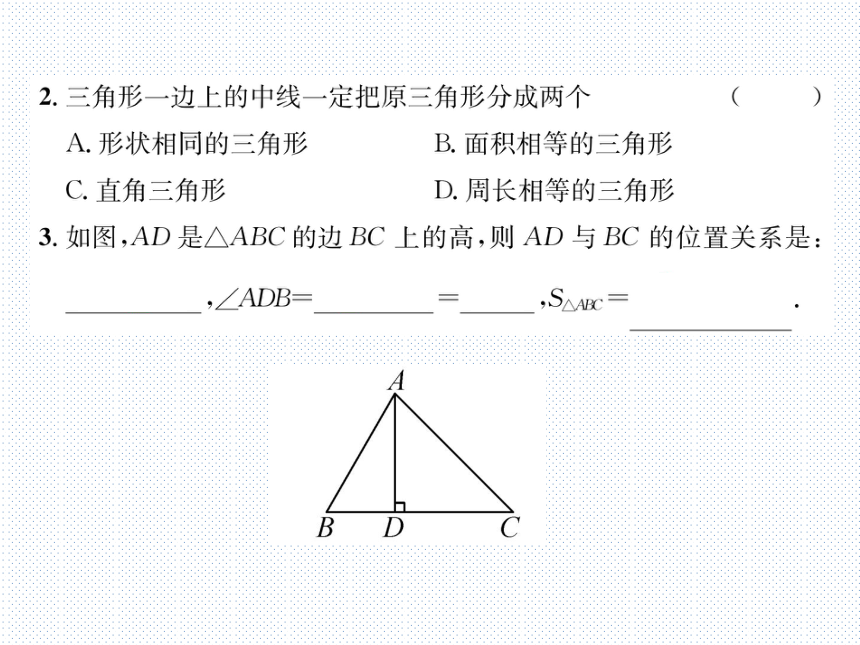
3.如图,AD是△ABC的边BC上的高,则AD与BC的位置关系是:
ADBC,∠ADB=∠ADC=90°,SMAIX=
BC·AD
D
(第3题图)
(第4题图)
(第5题图)
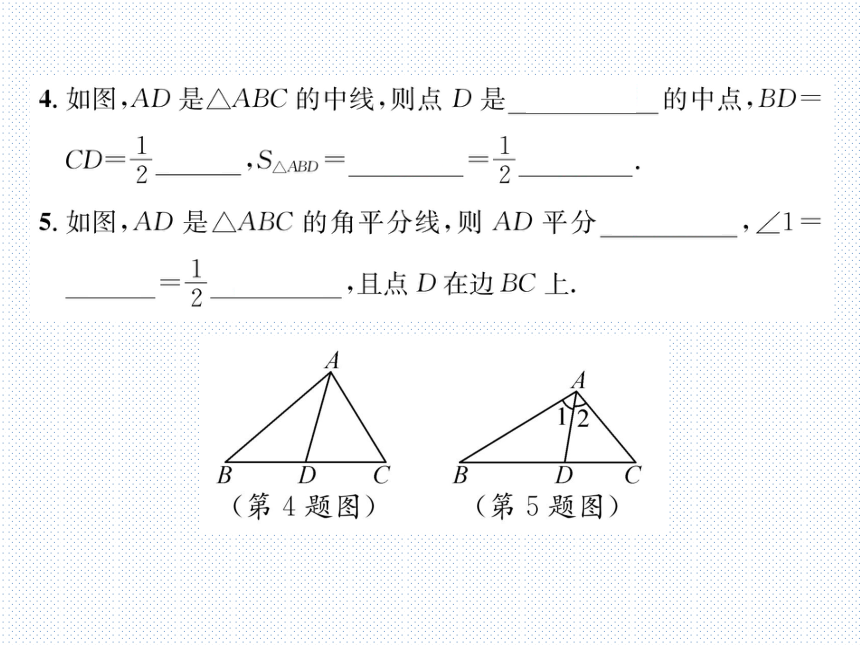
4.如图,AD是△ABC的中线,则点D是线段BC的中点,BD=
CD=BC,SAABD=SAACD-SAARC.
5.如图,AD是△ABC的角平分线,则AD平分
∠BAC,∠1=
∠2=2∠BAC,且点D在边BC上.
6.锐角三角形的三条高都在三角形内部,钝角三角形有2条
高在三角形外,直角三角形有两条高恰是它的直角边·
知识点②三角形的稳定性
7.如图,自行车的主框架采用了三角形结构,这样设计的依据是
三角形的稳定性·
B
DE C
(第7题图)
(第8题图)
易错点
对三角形的高的定义不理解而致错
8.如图,AD⊥BC于点D,那么图中以AD为高的三角形有6个.
能力提升
整合运用
9.如图,若∠1=∠2,∠3=∠4,则下列结论中错误的
是
(D
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.∠3=2∠ACB
D.CE是△ABC的角平分线
10.如图,在△ABC中,D,E,F分别是BC,AD,CE
的中点,S△ABc=4cm,则S△BEr等于
(B)
A.2 cm2
B.1 cm2
C.em D.cm
R
(第10题图)
(第11题图)
11.如图是一幅电动伸缩门的图片,则电动门能伸缩
的几何原理是四边形具有不稳定性·
12.如图,BD是△ABC的中线,AB=8,BC=6,
△ABD和△BCD的周长的差是2
(第12题图)
(第13题图)
13.(教材P,习题Ts变式)如图,在△ABC中,AD
BC,BE⊥AC,CF⊥AB,垂足分别是D,E,F.若
AC=4,AD=3,BE=2,则BC=
6
3
14.如图,已知△ABC,根据要求画图.
(1)画BC边上的高;
(2)画∠C的平分线:
(3)将△ABC分成面积相等的两部分,
解:如图,
(1)线段AD即为BC边上的高:
(2)CE即为∠ACB的平分线;
(3)中线BF将△ABC分成面积相等的两部分.
(此问答案不唯一)
知识构建
例题引路
台知识构建
高
三角形
相关
线段
中线
重心
角平分线
稳定性
例题引路
【例1】如图,在△ABC中,AE是中线,
AD是角平分线,AF是高,∠BAC=
70°,∠CAF=10°,BE=2,AF=3,填
空:
B ED FC
(1)∠BAD=
9
(2)∠DAF=
(3)SAAEC=
【名师点拨】注意三角形的中线平分三
角形的面积,
【学生解答】(1)35°;(2)25°;(3)3
【例2】桥梁拉杆、电视机底座都是三角形
结构,这是利用了三角形的
性.
【学生解答】稳定
【例3】如图,CD是△ABC的角平分
线,E是BC边上的一点,且∠1=∠2.
试判断DE与AC的位置关系并说明
理由.
B
【学生解答】解:DE∥AC.理由如下:
CD是△ABC的角平分线,
.∠ACD=∠1.
.∠1=∠2,
.∠ACD=∠2,
∴.DE∥AC.
基础过关
逐点击破
知识点①
,三角形的高、中线及角平分线的应用
1.以下是四位同学在钝角三角形ABC中画BC边上的高,其中画法正
确的是
(B
B
2.三角形一边上的中线一定把原三角形分成两个
(B
A.形状相同的三角形
B.面积相等的三角形
C.直角三角形
D.周长相等的三角形
3.如图,AD是△ABC的边BC上的高,则AD与BC的位置关系是:
ADBC,∠ADB=∠ADC=90°,SMAIX=
BC·AD
D
(第3题图)
(第4题图)
(第5题图)
4.如图,AD是△ABC的中线,则点D是线段BC的中点,BD=
CD=BC,SAABD=SAACD-SAARC.
5.如图,AD是△ABC的角平分线,则AD平分
∠BAC,∠1=
∠2=2∠BAC,且点D在边BC上.
6.锐角三角形的三条高都在三角形内部,钝角三角形有2条
高在三角形外,直角三角形有两条高恰是它的直角边·
知识点②三角形的稳定性
7.如图,自行车的主框架采用了三角形结构,这样设计的依据是
三角形的稳定性·
B
DE C
(第7题图)
(第8题图)
易错点
对三角形的高的定义不理解而致错
8.如图,AD⊥BC于点D,那么图中以AD为高的三角形有6个.
能力提升
整合运用
9.如图,若∠1=∠2,∠3=∠4,则下列结论中错误的
是
(D
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.∠3=2∠ACB
D.CE是△ABC的角平分线
10.如图,在△ABC中,D,E,F分别是BC,AD,CE
的中点,S△ABc=4cm,则S△BEr等于
(B)
A.2 cm2
B.1 cm2
C.em D.cm
R
(第10题图)
(第11题图)
11.如图是一幅电动伸缩门的图片,则电动门能伸缩
的几何原理是四边形具有不稳定性·
12.如图,BD是△ABC的中线,AB=8,BC=6,
△ABD和△BCD的周长的差是2
(第12题图)
(第13题图)
13.(教材P,习题Ts变式)如图,在△ABC中,AD
BC,BE⊥AC,CF⊥AB,垂足分别是D,E,F.若
AC=4,AD=3,BE=2,则BC=
6
3
14.如图,已知△ABC,根据要求画图.
(1)画BC边上的高;
(2)画∠C的平分线:
(3)将△ABC分成面积相等的两部分,
解:如图,
(1)线段AD即为BC边上的高:
(2)CE即为∠ACB的平分线;
(3)中线BF将△ABC分成面积相等的两部分.
(此问答案不唯一)
