人教版六上数学第八单元数学广角--数与形综合训练(二)(含答案)
文档属性
| 名称 | 人教版六上数学第八单元数学广角--数与形综合训练(二)(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 311.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 11:50:55 | ||
图片预览


文档简介
人教版六上第八单元数学广角--数与形综合训练(二)
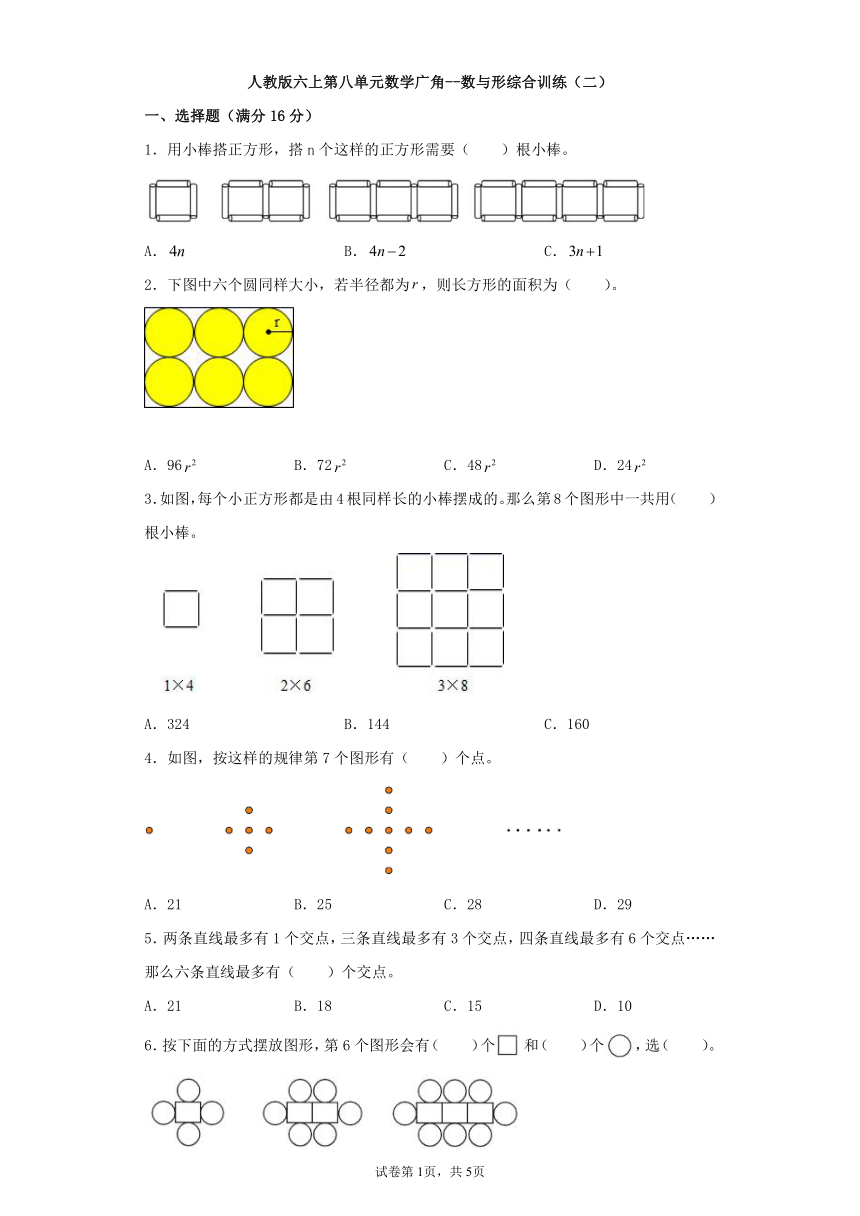
一、选择题(满分16分)
1.用小棒搭正方形,搭n个这样的正方形需要( )根小棒。
A. B. C.
2.下图中六个圆同样大小,若半径都为,则长方形的面积为( )。
A.96 B.72 C.48 D.24
3.如图,每个小正方形都是由4根同样长的小棒摆成的。那么第8个图形中一共用( )根小棒。
A.324 B.144 C.160
4.如图,按这样的规律第7个图形有( )个点。
A.21 B.25 C.28 D.29
5.两条直线最多有1个交点,三条直线最多有3个交点,四条直线最多有6个交点……那么六条直线最多有( )个交点。
A.21 B.18 C.15 D.10
6.按下面的方式摆放图形,第6个图形会有( )个和( )个,选( )。
A.6,8 B.6,10 C.6,12 D.6,14
7.一组图形有规律的排列着。○△□☆○△□☆○△□☆○△□☆…第79个是( )。
A.○ B.△ C.□ D.☆
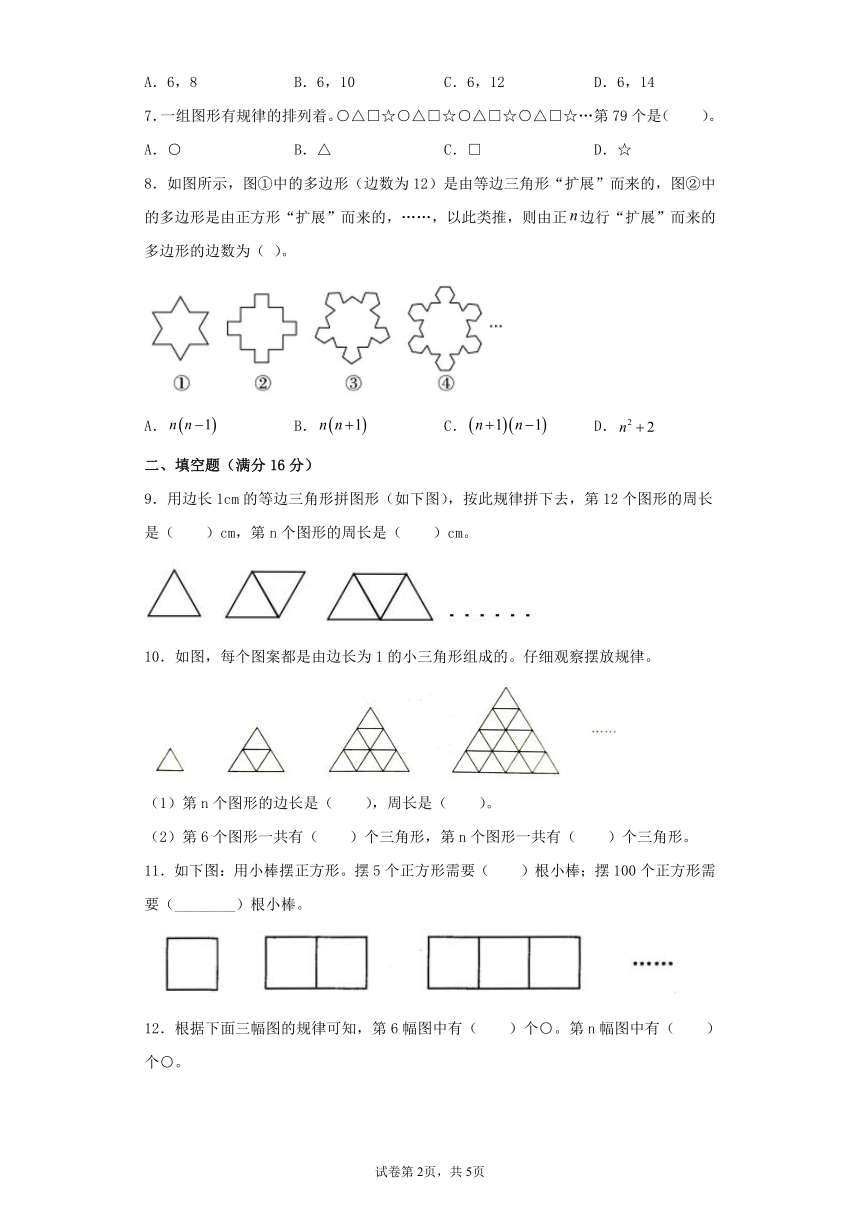
8.如图所示,图①中的多边形(边数为12)是由等边三角形“扩展”而来的,图②中的多边形是由正方形“扩展”而来的,……,以此类推,则由正边行“扩展”而来的多边形的边数为( )。
A. B. C. D.
二、填空题(满分16分)
9.用边长1cm的等边三角形拼图形(如下图),按此规律拼下去,第12个图形的周长是( )cm,第n个图形的周长是( )cm。
10.如图,每个图案都是由边长为1的小三角形组成的。仔细观察摆放规律。
(1)第n个图形的边长是( ),周长是( )。
(2)第6个图形一共有( )个三角形,第n个图形一共有( )个三角形。
11.如下图:用小棒摆正方形。摆5个正方形需要( )根小棒;摆100个正方形需要(________)根小棒。
12.根据下面三幅图的规律可知,第6幅图中有( )个○。第n幅图中有( )个○。
13.1+3+5+7+9=( )2=( )
++++=( )
14.找规律填空。
,,,…,则:1+3+5+7+9+11+…+48+49=( )2。
15.用黑白2种颜色的六边形地砖,按照规律,拼成下面三个图案:
第4个图案中有( )块白色图案,第8个图案中有( )块白色图案。
16.根据规律,在横线上画图。
( )
三、判断题(满分8分)
17.1+3+5+7+5+3+1=42+32。( )
18.摆1个△用3根小棒,摆2个△用5根小棒,摆3个△用7根小棒。照这样,摆5个△用11根小棒。( )
19.在中,从“1”到“15”的和是64.( )
20.在1+3+5+7+9+…中,从“1”到数“13”的和是49.( )
四、连线题(满分6分)
21.(6分)请你用线把点连起来,要求连接成正方形,使正方形的每个顶点都必须在这些给出的点上.比一比,看谁连接成的正方形最多.
五、作图题(满分12分)
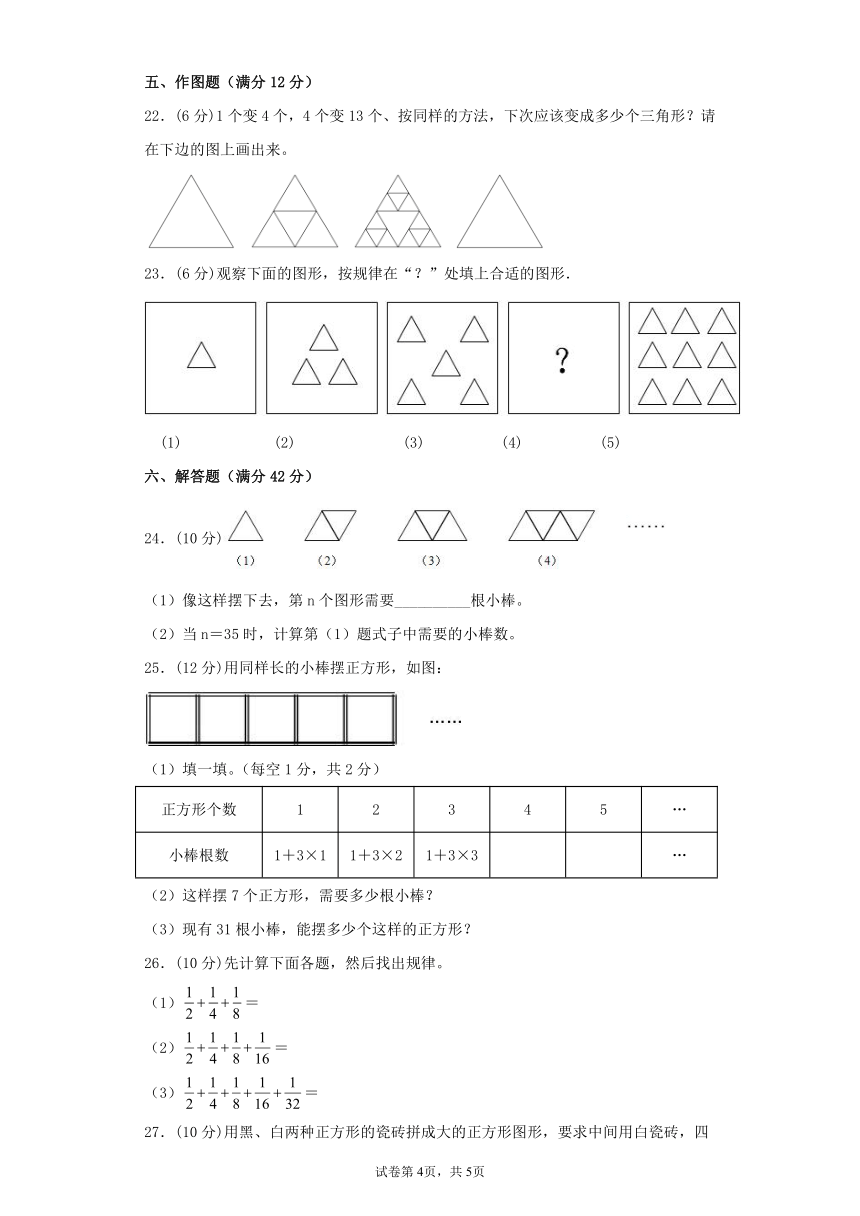
22.(6分)1个变4个,4个变13个、按同样的方法,下次应该变成多少个三角形?请在下边的图上画出来。
23.(6分)观察下面的图形,按规律在“?”处填上合适的图形.
(1) (2) (3) (4) (5)
六、解答题(满分42分)
24.(10分)
(1)像这样摆下去,第n个图形需要__________根小棒。
(2)当n=35时,计算第(1)题式子中需要的小棒数。
25.(12分)用同样长的小棒摆正方形,如图:
(1)填一填。(每空1分,共2分)
正方形个数 1 2 3 4 5 …
小棒根数 1+3×1 1+3×2 1+3×3 …
(2)这样摆7个正方形,需要多少根小棒?
(3)现有31根小棒,能摆多少个这样的正方形?
26.(10分)先计算下面各题,然后找出规律。
(1)=
(2)=
(3)=
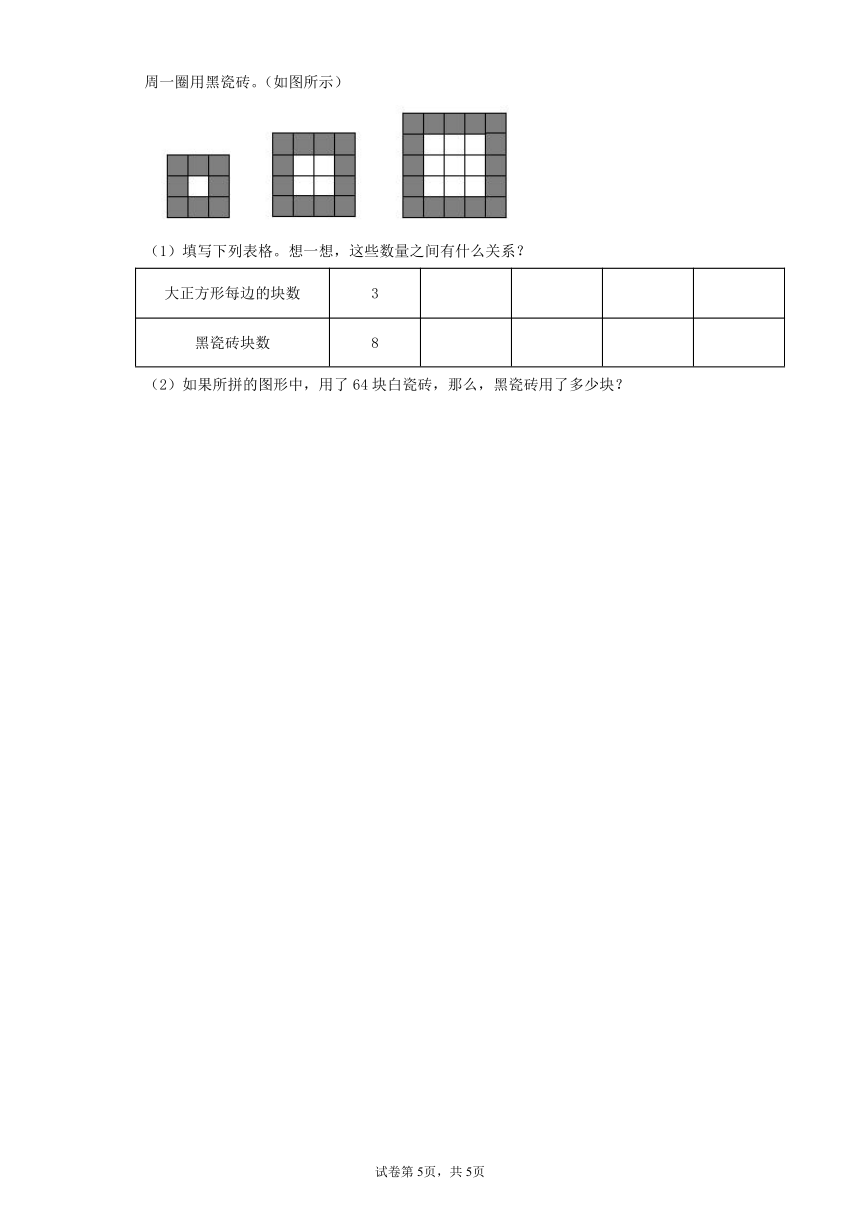
27.(10分)用黑、白两种正方形的瓷砖拼成大的正方形图形,要求中间用白瓷砖,四周一圈用黑瓷砖。(如图所示)
(1)填写下列表格。想一想,这些数量之间有什么关系?
大正方形每边的块数 3
黑瓷砖块数 8
(2)如果所拼的图形中,用了64块白瓷砖,那么,黑瓷砖用了多少块?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
2.D
3.B
4.B
5.C
6.D
7.C
8.B
9.14 n+2
10.n 3n 36 n2
11.16 301
12.36
13.5 25
14.25
15.18 34
16.
17.√
18.√
19.√
20.√
21.解:所以把所有的点连接起来,能组成5个正方形,并把四个小正方形的四条对角线围成的也是一个正方形,且每个正方形的顶点都在这些点上,则一共可以连接成5+1=6个正方形.如图:
22.
答:下次应该变成40个三角形。
23.
察下面的图形可知,按规律在“?”处填上7个三角形.
如图:
24.(1)根据分析可知,像这样摆下去,第n个图形需要(2n+1)根小棒。
(2)35×2+1
=70+1
= 71(根)
答:摆35个三角形需要71根小棒。
25.(1)
正方形个数 1 2 3 4 5 …
小棒根数 1+3×1 1+3×2 1+3×3 13 16 …
4个正方形小棒根数:1+3×4=13(根)
5个正方形小棒根数:1+3×5=16(根)
(2)1+3×7=22(根)
答:摆7个正方形,需要22根小棒。
(3)解:设31根小棒,能摆n个这样的正方形。
1+3n=31
3n=31-1
3n=30
n=30÷3
n=10
答:31根小棒,能摆10个这样的正方形。
26.(1),
=
=1-+-+-
=1-
=
(2)+++
=(1-)+(-)+(-)+(-)
=1+-+-+-
=1-
=
(3)++++
=(1-)+(-)+(-)+(-)+(-)
=1-+-+-+-+-
=1-
=
规律是:后一种加数是前一个加数的一半的连加算式的和是:1减最后一个加数的差,即分母是最后一个加数的分母,分子比分母少1。
27.(1)
大正方形每边的块数增加1块,所用的黑瓷砖数就增加4块;
(2)64=8×8;
(8+1)×4
=9×4
=36(块);
答:黑瓷砖用了36块。
答案第1页,共2页
答案第1页,共2页
一、选择题(满分16分)
1.用小棒搭正方形,搭n个这样的正方形需要( )根小棒。
A. B. C.
2.下图中六个圆同样大小,若半径都为,则长方形的面积为( )。
A.96 B.72 C.48 D.24
3.如图,每个小正方形都是由4根同样长的小棒摆成的。那么第8个图形中一共用( )根小棒。
A.324 B.144 C.160
4.如图,按这样的规律第7个图形有( )个点。
A.21 B.25 C.28 D.29
5.两条直线最多有1个交点,三条直线最多有3个交点,四条直线最多有6个交点……那么六条直线最多有( )个交点。
A.21 B.18 C.15 D.10
6.按下面的方式摆放图形,第6个图形会有( )个和( )个,选( )。
A.6,8 B.6,10 C.6,12 D.6,14
7.一组图形有规律的排列着。○△□☆○△□☆○△□☆○△□☆…第79个是( )。
A.○ B.△ C.□ D.☆
8.如图所示,图①中的多边形(边数为12)是由等边三角形“扩展”而来的,图②中的多边形是由正方形“扩展”而来的,……,以此类推,则由正边行“扩展”而来的多边形的边数为( )。
A. B. C. D.
二、填空题(满分16分)
9.用边长1cm的等边三角形拼图形(如下图),按此规律拼下去,第12个图形的周长是( )cm,第n个图形的周长是( )cm。
10.如图,每个图案都是由边长为1的小三角形组成的。仔细观察摆放规律。
(1)第n个图形的边长是( ),周长是( )。
(2)第6个图形一共有( )个三角形,第n个图形一共有( )个三角形。
11.如下图:用小棒摆正方形。摆5个正方形需要( )根小棒;摆100个正方形需要(________)根小棒。
12.根据下面三幅图的规律可知,第6幅图中有( )个○。第n幅图中有( )个○。
13.1+3+5+7+9=( )2=( )
++++=( )
14.找规律填空。
,,,…,则:1+3+5+7+9+11+…+48+49=( )2。
15.用黑白2种颜色的六边形地砖,按照规律,拼成下面三个图案:
第4个图案中有( )块白色图案,第8个图案中有( )块白色图案。
16.根据规律,在横线上画图。
( )
三、判断题(满分8分)
17.1+3+5+7+5+3+1=42+32。( )
18.摆1个△用3根小棒,摆2个△用5根小棒,摆3个△用7根小棒。照这样,摆5个△用11根小棒。( )
19.在中,从“1”到“15”的和是64.( )
20.在1+3+5+7+9+…中,从“1”到数“13”的和是49.( )
四、连线题(满分6分)
21.(6分)请你用线把点连起来,要求连接成正方形,使正方形的每个顶点都必须在这些给出的点上.比一比,看谁连接成的正方形最多.
五、作图题(满分12分)
22.(6分)1个变4个,4个变13个、按同样的方法,下次应该变成多少个三角形?请在下边的图上画出来。
23.(6分)观察下面的图形,按规律在“?”处填上合适的图形.
(1) (2) (3) (4) (5)
六、解答题(满分42分)
24.(10分)
(1)像这样摆下去,第n个图形需要__________根小棒。
(2)当n=35时,计算第(1)题式子中需要的小棒数。
25.(12分)用同样长的小棒摆正方形,如图:
(1)填一填。(每空1分,共2分)
正方形个数 1 2 3 4 5 …
小棒根数 1+3×1 1+3×2 1+3×3 …
(2)这样摆7个正方形,需要多少根小棒?
(3)现有31根小棒,能摆多少个这样的正方形?
26.(10分)先计算下面各题,然后找出规律。
(1)=
(2)=
(3)=
27.(10分)用黑、白两种正方形的瓷砖拼成大的正方形图形,要求中间用白瓷砖,四周一圈用黑瓷砖。(如图所示)
(1)填写下列表格。想一想,这些数量之间有什么关系?
大正方形每边的块数 3
黑瓷砖块数 8
(2)如果所拼的图形中,用了64块白瓷砖,那么,黑瓷砖用了多少块?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
2.D
3.B
4.B
5.C
6.D
7.C
8.B
9.14 n+2
10.n 3n 36 n2
11.16 301
12.36
13.5 25
14.25
15.18 34
16.
17.√
18.√
19.√
20.√
21.解:所以把所有的点连接起来,能组成5个正方形,并把四个小正方形的四条对角线围成的也是一个正方形,且每个正方形的顶点都在这些点上,则一共可以连接成5+1=6个正方形.如图:
22.
答:下次应该变成40个三角形。
23.
察下面的图形可知,按规律在“?”处填上7个三角形.
如图:
24.(1)根据分析可知,像这样摆下去,第n个图形需要(2n+1)根小棒。
(2)35×2+1
=70+1
= 71(根)
答:摆35个三角形需要71根小棒。
25.(1)
正方形个数 1 2 3 4 5 …
小棒根数 1+3×1 1+3×2 1+3×3 13 16 …
4个正方形小棒根数:1+3×4=13(根)
5个正方形小棒根数:1+3×5=16(根)
(2)1+3×7=22(根)
答:摆7个正方形,需要22根小棒。
(3)解:设31根小棒,能摆n个这样的正方形。
1+3n=31
3n=31-1
3n=30
n=30÷3
n=10
答:31根小棒,能摆10个这样的正方形。
26.(1),
=
=1-+-+-
=1-
=
(2)+++
=(1-)+(-)+(-)+(-)
=1+-+-+-
=1-
=
(3)++++
=(1-)+(-)+(-)+(-)+(-)
=1-+-+-+-+-
=1-
=
规律是:后一种加数是前一个加数的一半的连加算式的和是:1减最后一个加数的差,即分母是最后一个加数的分母,分子比分母少1。
27.(1)
大正方形每边的块数增加1块,所用的黑瓷砖数就增加4块;
(2)64=8×8;
(8+1)×4
=9×4
=36(块);
答:黑瓷砖用了36块。
答案第1页,共2页
答案第1页,共2页
