12.2.2 用“SAS”判定三角形全等 课件(共16张PPT)
文档属性
| 名称 | 12.2.2 用“SAS”判定三角形全等 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 939.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 22:33:18 | ||
图片预览




文档简介
(共16张PPT)
人教版 八年级上册
12.2全等三角形的判定
第2课时 用“SAS”判定三角形全等
情景导入
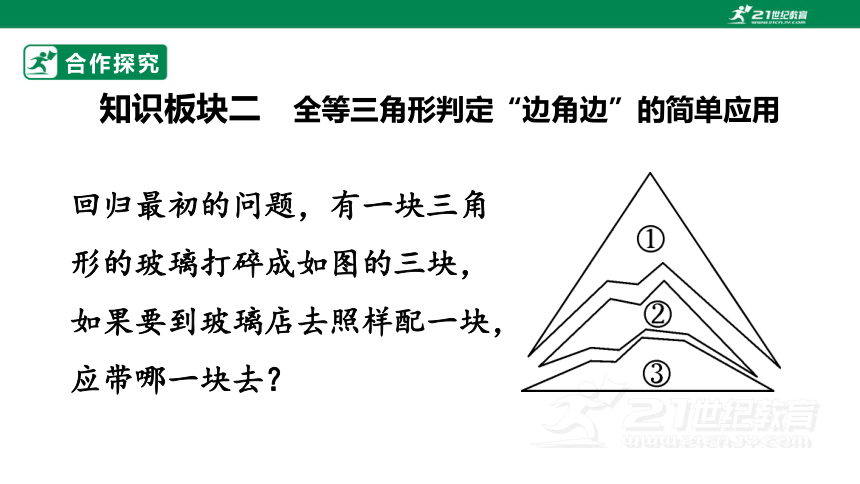
有一块三角形的玻璃打碎成如图的三块,如果要到玻璃店去照样配一块,应带哪一块去?
想一想
合作探究
知识板块一 判定两三角形全等的基本事实:“边角边”
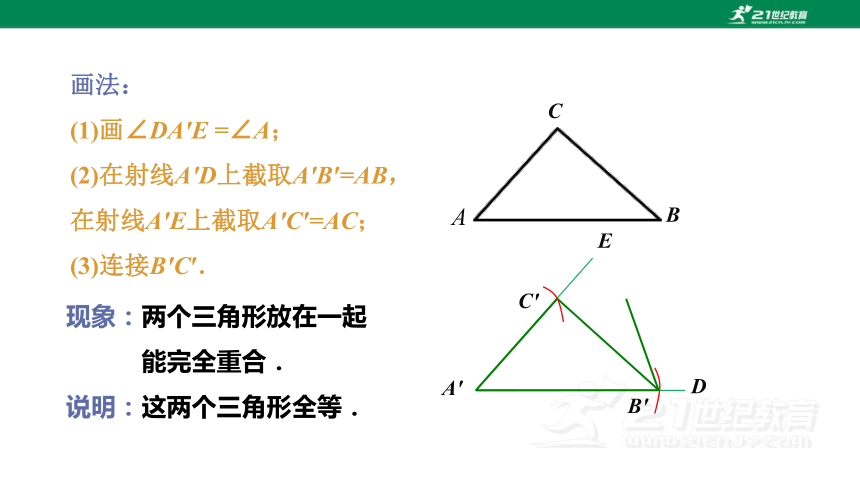
先任意画出一个△ABC.再画出一个△A′B′C′,
使A′B′=AB, A′C′=AC, ∠A′=∠A (即两边和它
们的夹角分别相等),把画好的△A′B′C′剪下来,
放到△ABC上,它们全等吗?
探究以下条件中的三角形是否全等
A
B
C
现象:两个三角形放在一起
能完全重合.
说明:这两个三角形全等.
画法:
(1)画∠DA′E =∠A;
(2)在射线A′D上截取A′B′=AB,
在射线A′E上截取A′C′=AC;
(3)连接B′C′.
A′
D
E
B′
C′
两个三角形全等的判定2:
两边和它们的夹角分别相等的两个三角形全等(简写成“边角边”或“SAS”).
几何语言:在△ABC和△A′B′C′中,
AB=A′B′,
∠ABC=∠A′B′C′,
BC=B′C′,
∴△ABC≌△A′B′C′.
∵
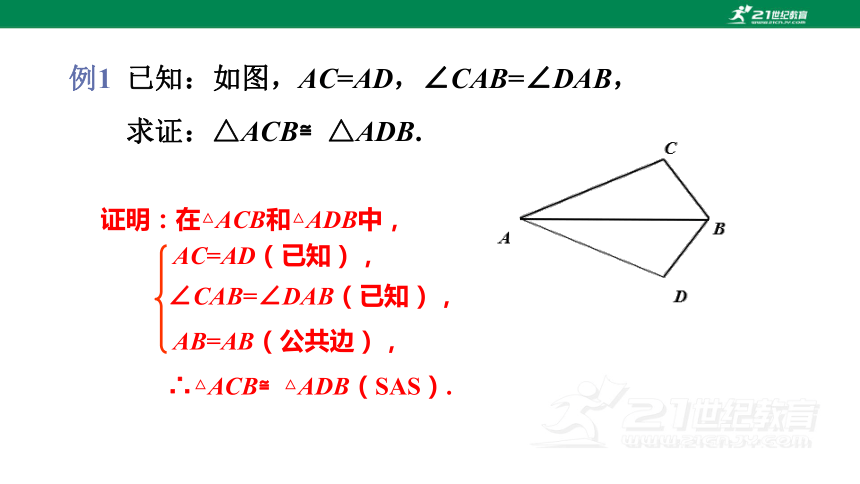
例1 已知:如图,AC=AD,∠CAB=∠DAB,
求证:△ACB≌△ADB.
AC=AD(已知),
∠CAB=∠DAB(已知),
AB=AB(公共边),
∴△ACB≌△ADB(SAS).
证明:在△ACB和△ADB中,
合作探究
知识板块二 全等三角形判定“边角边”的简单应用
回归最初的问题,有一块三角形的玻璃打碎成如图的三块,如果要到玻璃店去照样配一块,应带哪一块去?
利用今天所学“边角边”知识,带黑色的那块.因为它完整地保留了两边及其夹角,一个三角形两条边的长度和夹角的大小确定了,这个三角形的形状、大小就确定下来了.
如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从 点C不经过池塘可以直接到达点A和B. 连接AC 并延长到点D,使CD=CA.连接BC并延长到点 E,CE=CB.连接DE,那么量出的长就 是A,B的距离.为什么?
A
B
C
D
E
1
2
例2
分析:如果能证明△ABC≌△DEC ,就可以 得出
AB=DE.由题意可知,△ABC和△DEC 具备
“边角边”的条件.
证明:在△ABC和△DEC中,
CA=CD,
∠1=∠2,
CB=CE,
∴ △ABC≌△DEC(SAS).
∴ AB=DE.
当堂演练
1.如图,a,b,c分别表示△ABC的三边长,则下面与△ABC一定全等的三角形是( )
B
当堂演练
2.如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加的一个条件是( )
A.∠A=∠C
B.∠D=∠B
C.AD∥BC
D.DF∥BE
B
当堂演练
3.如图,AA′,BB′表示两根长度相同的木条,若O是AA′,BB′的中点,经测量AB=9 cm,则容器的内径A′B′为( )
A.8 cm
B.9 cm
C.10 cm
D.11 cm
B
当堂演练
4.如图,在△ABC和△ABD中,AC与BD相交于点E,AD=BC,∠DAB=∠CBA.
求证: AC=BD.
当堂演练
AD=BC,
∠DAB=∠CBA,
AB=BA
∴△BAD≌△ABC(SAS),
证明:在△ABC和△BAD中,
∴AC=BD.
板书设计
1.两边和它们的夹角分别相等的两个三角形全等,简写为“边角边”或“SAS”.
2.有两边和其中一边的对角分别相等的两个三角形不一定全等.
人教版 八年级上册
12.2全等三角形的判定
第2课时 用“SAS”判定三角形全等
情景导入
有一块三角形的玻璃打碎成如图的三块,如果要到玻璃店去照样配一块,应带哪一块去?
想一想
合作探究
知识板块一 判定两三角形全等的基本事实:“边角边”
先任意画出一个△ABC.再画出一个△A′B′C′,
使A′B′=AB, A′C′=AC, ∠A′=∠A (即两边和它
们的夹角分别相等),把画好的△A′B′C′剪下来,
放到△ABC上,它们全等吗?
探究以下条件中的三角形是否全等
A
B
C
现象:两个三角形放在一起
能完全重合.
说明:这两个三角形全等.
画法:
(1)画∠DA′E =∠A;
(2)在射线A′D上截取A′B′=AB,
在射线A′E上截取A′C′=AC;
(3)连接B′C′.
A′
D
E
B′
C′
两个三角形全等的判定2:
两边和它们的夹角分别相等的两个三角形全等(简写成“边角边”或“SAS”).
几何语言:在△ABC和△A′B′C′中,
AB=A′B′,
∠ABC=∠A′B′C′,
BC=B′C′,
∴△ABC≌△A′B′C′.
∵
例1 已知:如图,AC=AD,∠CAB=∠DAB,
求证:△ACB≌△ADB.
AC=AD(已知),
∠CAB=∠DAB(已知),
AB=AB(公共边),
∴△ACB≌△ADB(SAS).
证明:在△ACB和△ADB中,
合作探究
知识板块二 全等三角形判定“边角边”的简单应用
回归最初的问题,有一块三角形的玻璃打碎成如图的三块,如果要到玻璃店去照样配一块,应带哪一块去?
利用今天所学“边角边”知识,带黑色的那块.因为它完整地保留了两边及其夹角,一个三角形两条边的长度和夹角的大小确定了,这个三角形的形状、大小就确定下来了.
如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从 点C不经过池塘可以直接到达点A和B. 连接AC 并延长到点D,使CD=CA.连接BC并延长到点 E,CE=CB.连接DE,那么量出的长就 是A,B的距离.为什么?
A
B
C
D
E
1
2
例2
分析:如果能证明△ABC≌△DEC ,就可以 得出
AB=DE.由题意可知,△ABC和△DEC 具备
“边角边”的条件.
证明:在△ABC和△DEC中,
CA=CD,
∠1=∠2,
CB=CE,
∴ △ABC≌△DEC(SAS).
∴ AB=DE.
当堂演练
1.如图,a,b,c分别表示△ABC的三边长,则下面与△ABC一定全等的三角形是( )
B
当堂演练
2.如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加的一个条件是( )
A.∠A=∠C
B.∠D=∠B
C.AD∥BC
D.DF∥BE
B
当堂演练
3.如图,AA′,BB′表示两根长度相同的木条,若O是AA′,BB′的中点,经测量AB=9 cm,则容器的内径A′B′为( )
A.8 cm
B.9 cm
C.10 cm
D.11 cm
B
当堂演练
4.如图,在△ABC和△ABD中,AC与BD相交于点E,AD=BC,∠DAB=∠CBA.
求证: AC=BD.
当堂演练
AD=BC,
∠DAB=∠CBA,
AB=BA
∴△BAD≌△ABC(SAS),
证明:在△ABC和△BAD中,
∴AC=BD.
板书设计
1.两边和它们的夹角分别相等的两个三角形全等,简写为“边角边”或“SAS”.
2.有两边和其中一边的对角分别相等的两个三角形不一定全等.
