人教版七年级上册4.3.3余角和补角 课件(共21张PPT)
文档属性
| 名称 | 人教版七年级上册4.3.3余角和补角 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 15:54:07 | ||
图片预览






文档简介
(共21张PPT)
4.3.3 余角和补角
学习目标
1. 理解并掌握余角和补角的概念,了解方位角的概念.
2. 掌握余角和补角的性质,能运用余角与补角的性质解决实际问题.
3. 通过余角、补角性质的推导和应用,初步掌握图形语言与符号语言
之间的相互转化.
4. 在探究学习过程中,培养识图能力、知识运用能力,发展空间观念
进一步感受数学学习的意义.
余角和补角
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
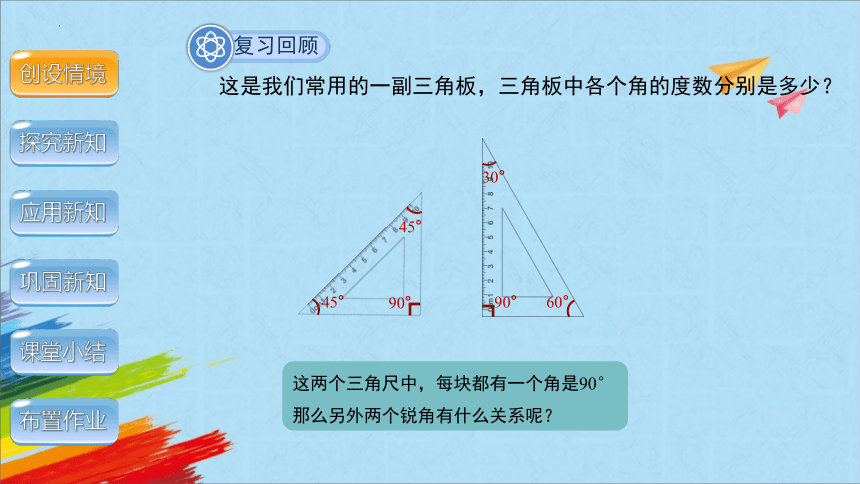
这是我们常用的一副三角板,三角板中各个角的度数分别是多少?
45°
90°
45°
30°
90°
60°
这两个三角尺中,每块都有一个角是90°
那么另外两个锐角有什么关系呢?
复习回顾
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
30°+60°=90° ,45°+45°=90°.
如果两个角的和等于90 (直角),就说这两个角互为余角(互余),
即其中每一个角是另一个角的余角.
即:若∠1+∠2=90°,
那么∠1和∠2互为余角.
∠1是∠2的余角,∠2也是∠1的余角.
30°的角和60°的角互余,45°的角和45°的角互余.
合作探究
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
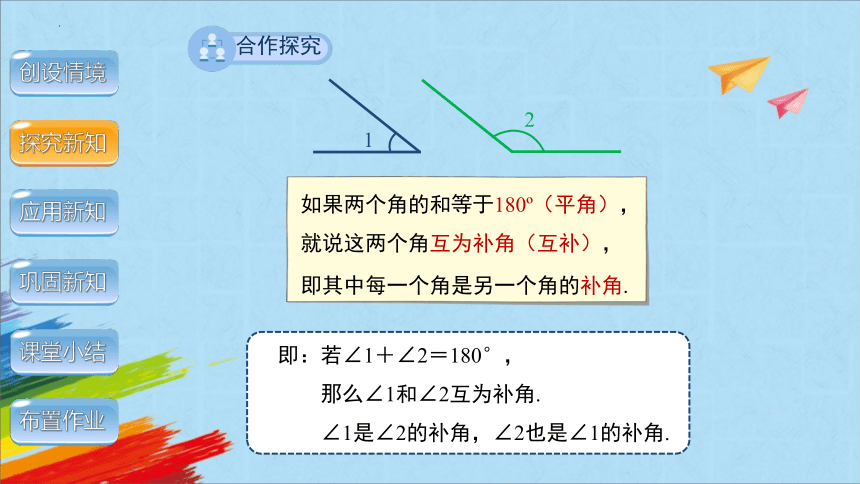
如果两个角的和等于180 (平角),就说这两个角互为补角(互补),
即其中每一个角是另一个角的补角.
即:若∠1+∠2=180°,
那么∠1和∠2互为补角.
∠1是∠2的补角,∠2也是∠1的补角.
1
2
合作探究
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
(1)若∠1与∠2互补,则∠1+∠2=______.
(2)∠1=90 -∠2,则∠1与∠2的关系为___________.
180°
互为余角
做一做
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
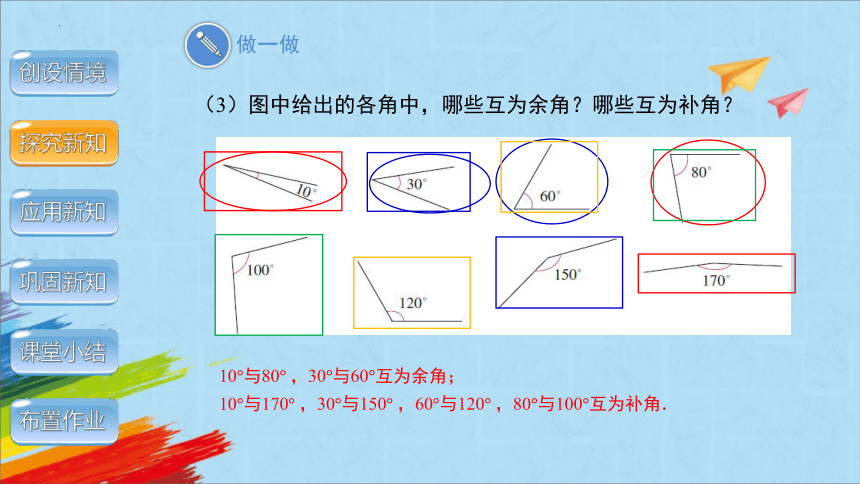
(3)图中给出的各角中,哪些互为余角?哪些互为补角?
做一做
10°与80° ,30°与60°互为余角;
10°与170° ,30°与150° ,60°与120° ,80°与100°互为补角.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
已知∠1与∠2,∠3都互为补角,那么∠2和∠3的大小有什么关系?
∠1与∠2和∠3都互为补角,
所以 ∠2=∠3.
结论
同角的补角相等.
那么 ∠2=180 -∠1,
∠3=180 -∠1,
问题
等角的补角是否也有类似性质?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
结论
等角的补角相等.
已知∠1与∠2互补,∠3与∠4互补.
若∠1=∠3,那么∠2和∠4 相等吗?为什么?
由∠1与∠2互补,得∠1+∠2=180 ,所以 ∠2=180 -∠1.
由∠3与∠4互补,得∠3+∠4=180 ,所以 ∠4=180 -∠3.
又因为∠1=∠3,180 -∠1=180 -∠3,所以∠2=∠4.
探究
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
对于余角是否也有类似性质?
补角的性质:同角(等角)的补角相等.
归纳
若∠1与∠2和∠3都互为余角,
所以 ∠2=∠3.
那么 ∠2=90 -∠1,
∠3=90 -∠1,
余角的性质:同角(等角)的余角相等.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
(1)若∠1与∠2互余,∠2与∠3互余,
则______=______,根据是_________ .
(2)若∠3与∠4互补,∠6与∠5互补,且∠3=∠6,
则______=______,根据是_______ __.
∠1
∠3
同角的余角相等
等角的补角相等
∠4
∠5
做一做
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
在航行、测绘等工作以及生活中,我们经常需要用方位角描述一个物体的方位,那么什么叫做方位角?如何用方位角描述方向呢?
方位角是表示方向的角.
A在O北偏东30°方向
B在O南偏西60°方向
以正北、正南方向为基准来描述物体所处的方向.
注意:方位角通常先写北或南,再写偏东或偏西.
如:“北偏东30°”一般不写成“东偏北60°”.
北
西
东
南
A
B
30°
60°
O
探究
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
在日常生活与实际应用中经常用到:
东北方向表示北偏东45°;西北方向表示北偏西45°;
东南方向表示南偏东45°;西南方向表示南偏西45°.
北
南
东
西
O
东北
东南
西南
45°
45°
45°
45°
西北
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
海上缉私艇发现离它500海里处停着一艘可疑船只,你能确定缉私艇的航线,并画出示意图吗?
可疑船
缉私艇
B
A
67°
北偏东67°
北
东
南
西
思考
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
例1 如图,点A,O,B在同一直线上,射线OD和射线OE分别
平分∠AOC 和 ∠BOC,图中哪些角互为余角?
解:
因为A,O,B在同一直线上,
所以∠AOC和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC,∠BOC,
所以∠COD +∠COE= ∠AOC+ ∠BOC
= (∠AOC+∠BOC )
=90°
所以, ∠COD 和∠COE互为余角,
同理, ∠AOD 和∠BOE,∠AOD和∠COE ,
∠COD 和∠BOE也互为余角.
典型例题
C
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
例2 如图,货轮O在航行过程中,发现灯塔A在它南偏东60 的方向上. 同时,在它北偏东40 、南偏西10 、西北(即北偏西45 )方向上又分别发现了客轮B,货轮C和海岛D.
仿照表示灯塔方位的方法,画出表示客轮B、货轮C和海岛D方向的射线.
O
●
东
南
西
北
● A
60°
40°
B
10°
45°
D
典型例题
解:
2.一个角的补角加上24°,恰好等于这个角的5倍,求这个角的度数.
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
1.已知∠α的补角是125°,则∠α的度数是( ).
A.55° B.65° C.75° D.85°
A
设这个角的度数为x°,依题意,得:
180-x+24=5x.
解得:x=34.
所以这个角的度数是34°.
随堂练习
解:
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
如图所示,
OB表示南偏东25°,
OC表示北偏西60°.
C
B
60°
30°
北
西
南
东
O
A
3.如图,OA是表示北偏东30°方向的一条射线,仿照这条射线画出
表示下列方向的射线:
(1)南偏东25°; (2)北偏西60°.
25°
随堂练习
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
余角和补角的性质:
互余和互补:
1.如果两个角的和等于90°(直角),就说这两个角互为余角,简称互余.
其中每一个角是另一个角的余角.
2.如果两个角的和等于180 °(平角),就说这两个角互为补角,简称互补.
其中每一个角是另一个角的补角.
1.同角(或等角)的余角相等.
2.同角(或等角)的补角相等.
余角和补角
方位角:
方位角是表示方向的角.
以正北、正南方向为基准来描述物体所处的方向.
布置作业
教科书第140页习题4.3
第11,12,13题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
4.3.3 余角和补角
学习目标
1. 理解并掌握余角和补角的概念,了解方位角的概念.
2. 掌握余角和补角的性质,能运用余角与补角的性质解决实际问题.
3. 通过余角、补角性质的推导和应用,初步掌握图形语言与符号语言
之间的相互转化.
4. 在探究学习过程中,培养识图能力、知识运用能力,发展空间观念
进一步感受数学学习的意义.
余角和补角
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
这是我们常用的一副三角板,三角板中各个角的度数分别是多少?
45°
90°
45°
30°
90°
60°
这两个三角尺中,每块都有一个角是90°
那么另外两个锐角有什么关系呢?
复习回顾
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
30°+60°=90° ,45°+45°=90°.
如果两个角的和等于90 (直角),就说这两个角互为余角(互余),
即其中每一个角是另一个角的余角.
即:若∠1+∠2=90°,
那么∠1和∠2互为余角.
∠1是∠2的余角,∠2也是∠1的余角.
30°的角和60°的角互余,45°的角和45°的角互余.
合作探究
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
如果两个角的和等于180 (平角),就说这两个角互为补角(互补),
即其中每一个角是另一个角的补角.
即:若∠1+∠2=180°,
那么∠1和∠2互为补角.
∠1是∠2的补角,∠2也是∠1的补角.
1
2
合作探究
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
(1)若∠1与∠2互补,则∠1+∠2=______.
(2)∠1=90 -∠2,则∠1与∠2的关系为___________.
180°
互为余角
做一做
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
(3)图中给出的各角中,哪些互为余角?哪些互为补角?
做一做
10°与80° ,30°与60°互为余角;
10°与170° ,30°与150° ,60°与120° ,80°与100°互为补角.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
已知∠1与∠2,∠3都互为补角,那么∠2和∠3的大小有什么关系?
∠1与∠2和∠3都互为补角,
所以 ∠2=∠3.
结论
同角的补角相等.
那么 ∠2=180 -∠1,
∠3=180 -∠1,
问题
等角的补角是否也有类似性质?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
结论
等角的补角相等.
已知∠1与∠2互补,∠3与∠4互补.
若∠1=∠3,那么∠2和∠4 相等吗?为什么?
由∠1与∠2互补,得∠1+∠2=180 ,所以 ∠2=180 -∠1.
由∠3与∠4互补,得∠3+∠4=180 ,所以 ∠4=180 -∠3.
又因为∠1=∠3,180 -∠1=180 -∠3,所以∠2=∠4.
探究
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
对于余角是否也有类似性质?
补角的性质:同角(等角)的补角相等.
归纳
若∠1与∠2和∠3都互为余角,
所以 ∠2=∠3.
那么 ∠2=90 -∠1,
∠3=90 -∠1,
余角的性质:同角(等角)的余角相等.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
(1)若∠1与∠2互余,∠2与∠3互余,
则______=______,根据是_________ .
(2)若∠3与∠4互补,∠6与∠5互补,且∠3=∠6,
则______=______,根据是_______ __.
∠1
∠3
同角的余角相等
等角的补角相等
∠4
∠5
做一做
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
在航行、测绘等工作以及生活中,我们经常需要用方位角描述一个物体的方位,那么什么叫做方位角?如何用方位角描述方向呢?
方位角是表示方向的角.
A在O北偏东30°方向
B在O南偏西60°方向
以正北、正南方向为基准来描述物体所处的方向.
注意:方位角通常先写北或南,再写偏东或偏西.
如:“北偏东30°”一般不写成“东偏北60°”.
北
西
东
南
A
B
30°
60°
O
探究
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
在日常生活与实际应用中经常用到:
东北方向表示北偏东45°;西北方向表示北偏西45°;
东南方向表示南偏东45°;西南方向表示南偏西45°.
北
南
东
西
O
东北
东南
西南
45°
45°
45°
45°
西北
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
海上缉私艇发现离它500海里处停着一艘可疑船只,你能确定缉私艇的航线,并画出示意图吗?
可疑船
缉私艇
B
A
67°
北偏东67°
北
东
南
西
思考
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
例1 如图,点A,O,B在同一直线上,射线OD和射线OE分别
平分∠AOC 和 ∠BOC,图中哪些角互为余角?
解:
因为A,O,B在同一直线上,
所以∠AOC和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC,∠BOC,
所以∠COD +∠COE= ∠AOC+ ∠BOC
= (∠AOC+∠BOC )
=90°
所以, ∠COD 和∠COE互为余角,
同理, ∠AOD 和∠BOE,∠AOD和∠COE ,
∠COD 和∠BOE也互为余角.
典型例题
C
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
例2 如图,货轮O在航行过程中,发现灯塔A在它南偏东60 的方向上. 同时,在它北偏东40 、南偏西10 、西北(即北偏西45 )方向上又分别发现了客轮B,货轮C和海岛D.
仿照表示灯塔方位的方法,画出表示客轮B、货轮C和海岛D方向的射线.
O
●
东
南
西
北
● A
60°
40°
B
10°
45°
D
典型例题
解:
2.一个角的补角加上24°,恰好等于这个角的5倍,求这个角的度数.
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
1.已知∠α的补角是125°,则∠α的度数是( ).
A.55° B.65° C.75° D.85°
A
设这个角的度数为x°,依题意,得:
180-x+24=5x.
解得:x=34.
所以这个角的度数是34°.
随堂练习
解:
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
如图所示,
OB表示南偏东25°,
OC表示北偏西60°.
C
B
60°
30°
北
西
南
东
O
A
3.如图,OA是表示北偏东30°方向的一条射线,仿照这条射线画出
表示下列方向的射线:
(1)南偏东25°; (2)北偏西60°.
25°
随堂练习
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
余角和补角的性质:
互余和互补:
1.如果两个角的和等于90°(直角),就说这两个角互为余角,简称互余.
其中每一个角是另一个角的余角.
2.如果两个角的和等于180 °(平角),就说这两个角互为补角,简称互补.
其中每一个角是另一个角的补角.
1.同角(或等角)的余角相等.
2.同角(或等角)的补角相等.
余角和补角
方位角:
方位角是表示方向的角.
以正北、正南方向为基准来描述物体所处的方向.
布置作业
教科书第140页习题4.3
第11,12,13题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
