人教版七年级上册4.2直线、射线、线段(第2课时) 课件(共23张PPT)
文档属性
| 名称 | 人教版七年级上册4.2直线、射线、线段(第2课时) 课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 16:00:16 | ||
图片预览






文档简介
(共23张PPT)
4.2 直线、射线、线段
第 2 课时
学习目标
1. 会用尺规作图画一条线段等于已知线段,会比较两条线段的长短.
2. 理解线段等分点的意义.
3. 体会文字语言、符号语言和图形语言的相互转化.
4. 培养学生对几何图形的兴趣,提高学习几何的积极性.
重点
直线
射线
线段
难点
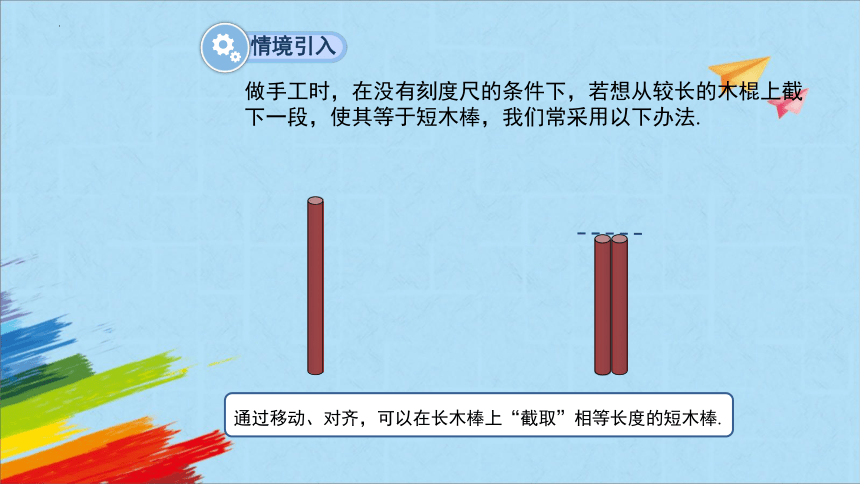
做手工时,在没有刻度尺的条件下,若想从较长的木棍上截下一段,使其等于短木棒,我们常采用以下办法.
情境引入
通过移动、对齐,可以在长木棒上“截取”相等长度的短木棒.
思考
圆规可截取任意长度,相当于可以移动的“小木棍”.
在只有圆规和无刻度的直尺的情况下,大家想想办法,如何画出一条与已知线段相等的线段?
a
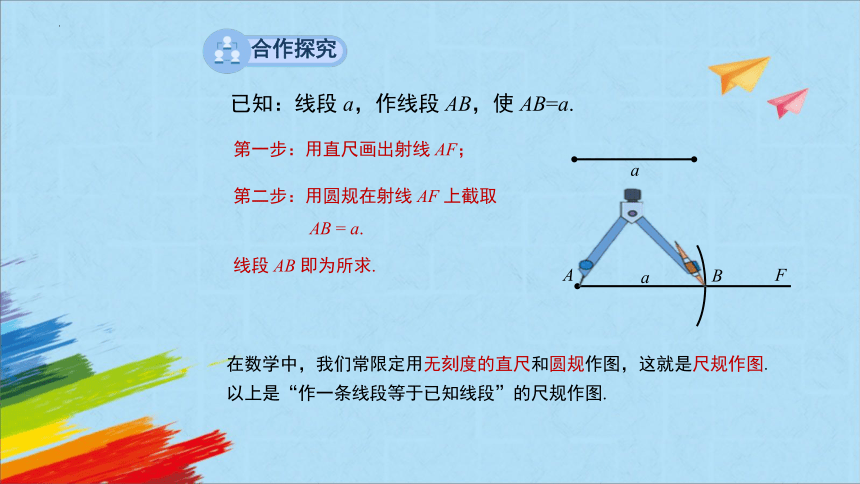
已知:线段 a,作线段 AB,使 AB=a.
第一步:用直尺画出射线 AF;
第二步:用圆规在射线 AF 上截取
AB = a.
线段 AB 即为所求.
a
A F
a
B
在数学中,我们常限定用无刻度的直尺和圆规作图,这就是尺规作图.
以上是“作一条线段等于已知线段”的尺规作图.
合作探究
如何比较两个同学的身高?
思考
方法:
目测法:准确率太低;
测量法:先测量出两人的身高,再比较;
脚等高:站在同一水平线上,看头顶高低.
类比上面的方法,你能比较两条线段的长短吗?
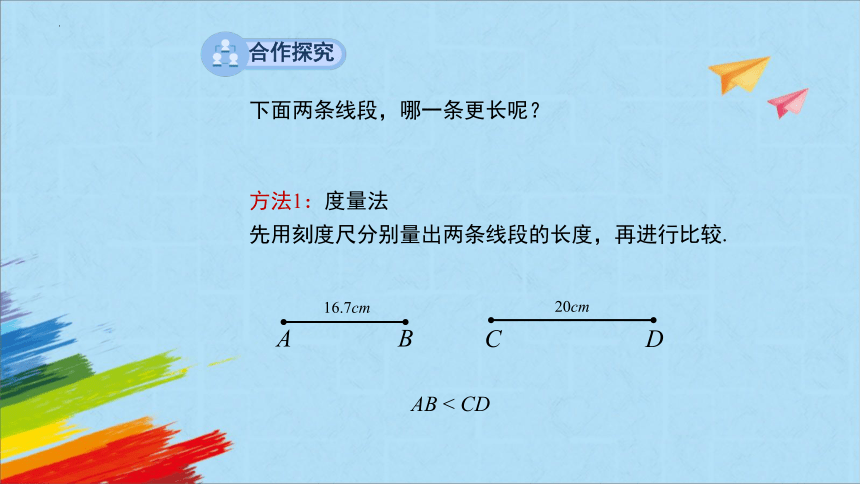
下面两条线段,哪一条更长呢?
C D
A B
16.7cm
20cm
AB < CD
方法1:度量法
先用刻度尺分别量出两条线段的长度,再进行比较.
合作探究
思考
C D
A B
AB方法2:叠合法
移动其中一条线段,使它们有一个端点重合,
然后根据另一个端点的位置,进行判断.
下面两条线段,哪一条更长呢?
若点 A 与点 C 重合,点 B 落在C,D之间,那么 AB CD.
(A)
B
<
B
A
C
D
叠合法可能会出现哪些情况?
交流
情形一:
思考
若点 A 与点 C 重合,点 B 与点 D重合,那么 AB ___ CD.
=
C
D
A
B
(A)
(B)
情形二:
叠合法可能会出现哪些情况?
思考
若点 A 与点 C 重合,点 B 落在 CD 的延长线上,那么 AB CD.
>
C
D
B
(A)
B
A
情形三:
叠合法可能会出现哪些情况?
比较线段长短的方法.
(1) 度量法:先利用刻度尺分别测量出两条直线的长度,然后根据测量结果进行比较;
C D
A B
(2) 叠合法:移动其中的一条线段,使其一个端点与另一条线段的一个端点重合,然后根据另一个端点的位置进行比较.
归纳
已知线段a,b,尝试用尺规作图作线段的和a+b.
a
b
A
B
a
C
b
(1)用直尺画出直线.
(2)用圆规在直线上作线段 AB = a;
在AB延长线上作线段 BC=b.
则线段 AC 就是 a 与 b 的和,记作 AC=a+b.
探究
已知线段a,b(a>b),尝试用尺规作图作线段的差a-b.
a
b
A
B
a
D
b
(1)用直尺画出直线.
(2)用圆规在直线上作线段 AB = a;
在线段 AB 上作线段 BD=b.
则线段 AD 就是 a 与 b 的差,记作 AD = a-b.
探究
思考
在纸片上画一条线段,折叠纸片,使线段的端点重合.
折痕与线段的交点处于线段的什么位置?
A
B
M
点 M 把线段 AB 分成相等的两条线段AM 与 BM,点 M 叫做线段 AB 的中点.
如图,点 M 为线段 AB 的中点.
A
B
M
归纳
已知AM=MB,M 就是线段AB的中点吗?
反之也成立:因为AM =MB = AB (或 AB = 2 AM = 2 MB),
所以 M 是线段 AB 的中点.
几何语言:因为 M 是线段 AB 的中点,
所以 AM = MB = AB (或 AB = 2AM = 2MB).
类似地,还有线段的三等分点、四等分点等.
N
M
B
A
线段的三等分点
线段的四等分点
A
O
P
Q
B
(或 AB = 3AM = 3MN = 3NB)
(或 AB = 4AO = 4OP = 4PQ = 4QB)
线段的三等分点有两个、线段的四等分点有三个.
探究
AM = MN = NB = AB
AO = OP = PQ = QB = AB
比较线段的长短:
(1)度量法;(2)叠合法.
归纳总结
尺规作图:
在数学中,常限定用无刻度的直尺和圆规作图,这就是尺规作图.
线段的中点:
把线段分为两条相等的线段的点,叫做这条线段的中点.
典型例题
如图,线段 AB=4,点 O 是线段 AB 上一点,C,D 分别是线段 OA,OB 的中点,求线段 CD 的长.
解:
因为 C,D 分别是线段 OA,OB 的中点,
所以 OC= AO,OD= BO.
所以 CD=OC+OD= (OA+OB)= AB= 4=2.
A C O D B
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
估计下列图中线段AB与线段AC的大小关系,再检验你的估计.
刻度尺:
AB<AC
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
估计下列图中线段AB与线段AC的大小关系,再检验你的估计.
圆规:
AB<AC
B′
探究新知
应用新知
布置作业
课堂小结
尺规作图:
比较线段的长短:
(1)度量法;(2)叠合法.
在数学中,常限定用无刻度的直尺和圆规作图,这就是尺规作图.
直线
射线
线段
线段的中点:
把线段分为两条相等的线段的点,叫做这条线段的中点.
布置作业
教科书第130页 习题4.2
第7,9,10题
探究新知
应用新知
课堂小结
4.2 直线、射线、线段
第 2 课时
学习目标
1. 会用尺规作图画一条线段等于已知线段,会比较两条线段的长短.
2. 理解线段等分点的意义.
3. 体会文字语言、符号语言和图形语言的相互转化.
4. 培养学生对几何图形的兴趣,提高学习几何的积极性.
重点
直线
射线
线段
难点
做手工时,在没有刻度尺的条件下,若想从较长的木棍上截下一段,使其等于短木棒,我们常采用以下办法.
情境引入
通过移动、对齐,可以在长木棒上“截取”相等长度的短木棒.
思考
圆规可截取任意长度,相当于可以移动的“小木棍”.
在只有圆规和无刻度的直尺的情况下,大家想想办法,如何画出一条与已知线段相等的线段?
a
已知:线段 a,作线段 AB,使 AB=a.
第一步:用直尺画出射线 AF;
第二步:用圆规在射线 AF 上截取
AB = a.
线段 AB 即为所求.
a
A F
a
B
在数学中,我们常限定用无刻度的直尺和圆规作图,这就是尺规作图.
以上是“作一条线段等于已知线段”的尺规作图.
合作探究
如何比较两个同学的身高?
思考
方法:
目测法:准确率太低;
测量法:先测量出两人的身高,再比较;
脚等高:站在同一水平线上,看头顶高低.
类比上面的方法,你能比较两条线段的长短吗?
下面两条线段,哪一条更长呢?
C D
A B
16.7cm
20cm
AB < CD
方法1:度量法
先用刻度尺分别量出两条线段的长度,再进行比较.
合作探究
思考
C D
A B
AB
移动其中一条线段,使它们有一个端点重合,
然后根据另一个端点的位置,进行判断.
下面两条线段,哪一条更长呢?
若点 A 与点 C 重合,点 B 落在C,D之间,那么 AB CD.
(A)
B
<
B
A
C
D
叠合法可能会出现哪些情况?
交流
情形一:
思考
若点 A 与点 C 重合,点 B 与点 D重合,那么 AB ___ CD.
=
C
D
A
B
(A)
(B)
情形二:
叠合法可能会出现哪些情况?
思考
若点 A 与点 C 重合,点 B 落在 CD 的延长线上,那么 AB CD.
>
C
D
B
(A)
B
A
情形三:
叠合法可能会出现哪些情况?
比较线段长短的方法.
(1) 度量法:先利用刻度尺分别测量出两条直线的长度,然后根据测量结果进行比较;
C D
A B
(2) 叠合法:移动其中的一条线段,使其一个端点与另一条线段的一个端点重合,然后根据另一个端点的位置进行比较.
归纳
已知线段a,b,尝试用尺规作图作线段的和a+b.
a
b
A
B
a
C
b
(1)用直尺画出直线.
(2)用圆规在直线上作线段 AB = a;
在AB延长线上作线段 BC=b.
则线段 AC 就是 a 与 b 的和,记作 AC=a+b.
探究
已知线段a,b(a>b),尝试用尺规作图作线段的差a-b.
a
b
A
B
a
D
b
(1)用直尺画出直线.
(2)用圆规在直线上作线段 AB = a;
在线段 AB 上作线段 BD=b.
则线段 AD 就是 a 与 b 的差,记作 AD = a-b.
探究
思考
在纸片上画一条线段,折叠纸片,使线段的端点重合.
折痕与线段的交点处于线段的什么位置?
A
B
M
点 M 把线段 AB 分成相等的两条线段AM 与 BM,点 M 叫做线段 AB 的中点.
如图,点 M 为线段 AB 的中点.
A
B
M
归纳
已知AM=MB,M 就是线段AB的中点吗?
反之也成立:因为AM =MB = AB (或 AB = 2 AM = 2 MB),
所以 M 是线段 AB 的中点.
几何语言:因为 M 是线段 AB 的中点,
所以 AM = MB = AB (或 AB = 2AM = 2MB).
类似地,还有线段的三等分点、四等分点等.
N
M
B
A
线段的三等分点
线段的四等分点
A
O
P
Q
B
(或 AB = 3AM = 3MN = 3NB)
(或 AB = 4AO = 4OP = 4PQ = 4QB)
线段的三等分点有两个、线段的四等分点有三个.
探究
AM = MN = NB = AB
AO = OP = PQ = QB = AB
比较线段的长短:
(1)度量法;(2)叠合法.
归纳总结
尺规作图:
在数学中,常限定用无刻度的直尺和圆规作图,这就是尺规作图.
线段的中点:
把线段分为两条相等的线段的点,叫做这条线段的中点.
典型例题
如图,线段 AB=4,点 O 是线段 AB 上一点,C,D 分别是线段 OA,OB 的中点,求线段 CD 的长.
解:
因为 C,D 分别是线段 OA,OB 的中点,
所以 OC= AO,OD= BO.
所以 CD=OC+OD= (OA+OB)= AB= 4=2.
A C O D B
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
估计下列图中线段AB与线段AC的大小关系,再检验你的估计.
刻度尺:
AB<AC
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
估计下列图中线段AB与线段AC的大小关系,再检验你的估计.
圆规:
AB<AC
B′
探究新知
应用新知
布置作业
课堂小结
尺规作图:
比较线段的长短:
(1)度量法;(2)叠合法.
在数学中,常限定用无刻度的直尺和圆规作图,这就是尺规作图.
直线
射线
线段
线段的中点:
把线段分为两条相等的线段的点,叫做这条线段的中点.
布置作业
教科书第130页 习题4.2
第7,9,10题
探究新知
应用新知
课堂小结
