2022-2023学年人教版七年级数学上册4.2直线、射线、线段 第1课时 课件(共19张PPT)
文档属性
| 名称 | 2022-2023学年人教版七年级数学上册4.2直线、射线、线段 第1课时 课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 16:01:53 | ||
图片预览




文档简介
(共19张PPT)
4.2 直线、射线、线段
第 1 课时
学习目标
1. 了解线段、射线、直线的特征及表示方法.
2. 体会射线、直线的无限延伸,归纳线段、直线和射线三者之间的
联系与区别.
3. 通过直线、射线、线段概念的教学,培养学生的几何想象能力和
观察能力.
4. 培养学生对几何图形的兴趣,提高学习几何的积极性.
重点
直线
射线
线段
难点
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
请分别画出一条直线,一条射线和一条线段,然后说说
它们之间的联系与区别.
线段
射线
直线
复习回顾
区别:直线没有端点,射线有一个端点,线段有两个端点.
联系:都是直直的线.
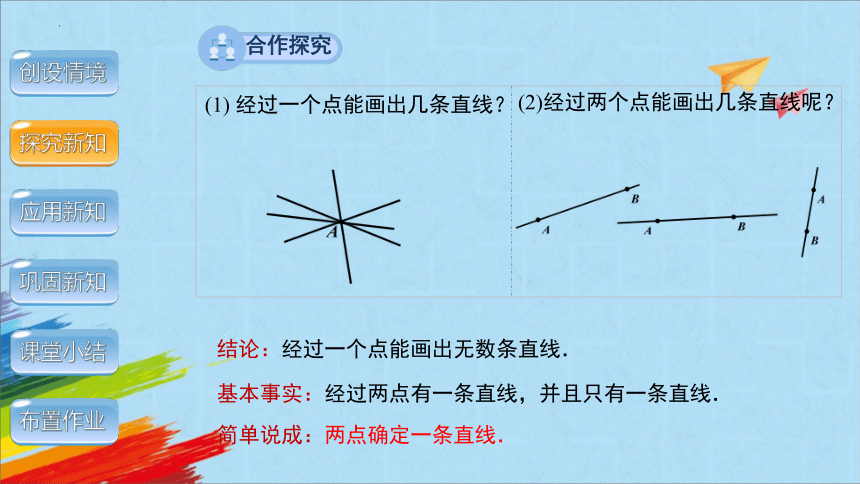
(1) 经过一个点能画出几条直线?
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
结论:经过一个点能画出无数条直线.
合作探究
(2)经过两个点能画出几条直线呢?
基本事实:经过两点有一条直线,并且只有一条直线.
简单说成:两点确定一条直线.
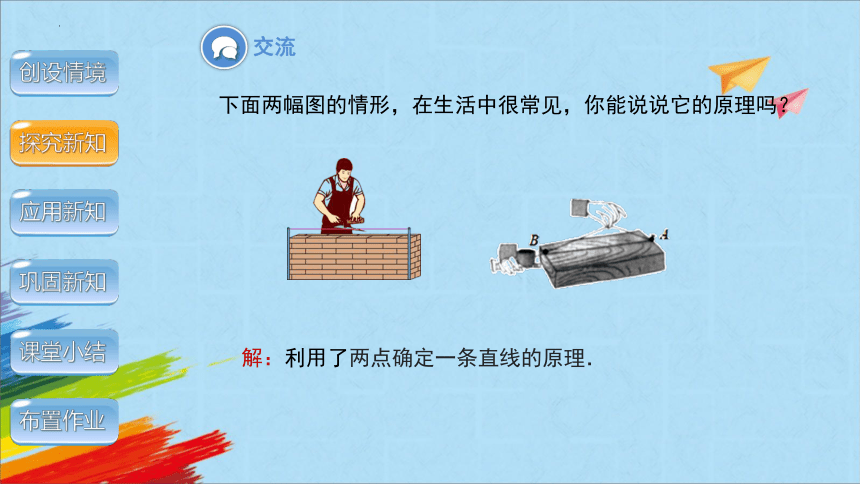
下面两幅图的情形,在生活中很常见,你能说说它的原理吗?
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
交流
解:利用了两点确定一条直线的原理.
一般地,几何图形都有对应的符号语言表示,直线如何表示呢?
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
1.用一个小写的英文字母表示,如:直线l.
2.用直线上的两个点来表示,如:直线AB(或直线BA).
l
A B
合作探究
同时,也可以说点A、B在直线l上
l
结论:一个点在一条直线上,也可以说这条直线经过这个点.
一个点在一条直线外,也可以说这条直线不经过这个点.
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
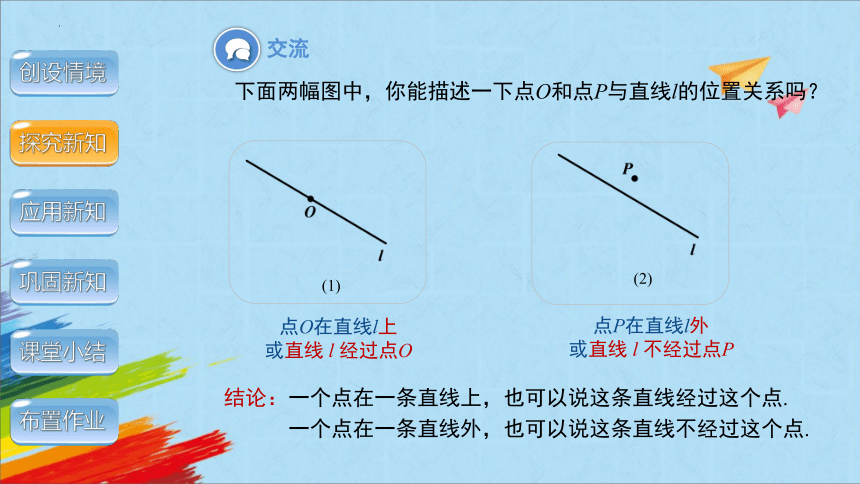
下面两幅图中,你能描述一下点O和点P与直线l的位置关系吗?
点O在直线l上
或直线 l 经过点O
(1)
(2)
点P在直线l外
或直线 l 不经过点P
交流
下面的两幅图中分别能画出几条直线?
用数学语言描述图中点与直线PQ的位置关系.
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
(2)可以画出3条直线;
点O在直线PQ外,点P在直线PQ上,点Q在直线PQ上.
思考
P
Q
P
Q
解:(1)可以画出1条直线;
点O、P、Q三点共线,且都在直线PQ上
(1)
(2)
当两条不同的直线有一个公共点时,我们称这两条直线相交,这个公共点叫做它们的交点 .
应用新知
巩固新知
课堂小结
布置作业
探究新知
思考
创设情境
如图:直线a和直线b相交于点O.
点O叫做交点
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
线段a 线段AB 线段BA
a
A
B
射线l 射线OA(端点字母在前)
注意:用两个大写字母表示射线或线段.
(1)表示射线时,前一个字母表示射线的端点,
后一个字母表示射线上除端点外的任意一点.
(2)表示线段时,两个字母的顺序无特殊要求.
线段和射线都是直线的一部分,类比直线的表示方法,
线段和射线又如何表示呢?
图形
表示方法
探究
基本事实:
经过两点有一条直线,并且只有一条直线.
简单记为:两点确定一条直线.
归纳总结
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
直线、射线、线段的表示方法:
(1)用一个小写英文字母表示;
(2)用线上的两个点表示.
直线l或直线 AB(BA)
射线l或射线OA
线段 a或线段 AB(BA)
点与直线的位置关系:
(1)点在直线上(直线经过点);
(2)点在直线外(直线不经过点).
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例1 如左图,用一个钉子把一根细木条钉在墙上,木条能绕着钉子转动,这表明过一个点__________________;
如右图,用两个钉子把细木条钉在墙上,就能固定细木条,这表明 .
可以画无数条直线
两点确定一条直线
(1)
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例2 读下列语句,分别画出图形.
(1)直线AB经过点M ,点N在直线AB外;
(2)线段AB与线段CD相交于点O;
(3)射线OA.
例2 读下列语句,分别画出图形.
(1)直线AB经过点M ,点N在直线AB外;
(2)线段AB与线段CD相交于点O;
(3)射线OA.
(2)
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
D
C
O
例2 读下列语句,分别画出图形.
(1)直线AB经过点M ,点N在直线AB外;
(2)线段AB与线段CD相交于点O;
(3)射线OA.
(3)
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
判断下列说法是否正确,并说明理由.
(1)线段AB和射线AB都是直线AB的一部分. ( )
(2)直线AB和直线BA是同一条直线. ( )
(3)射线AB和射线BA是同一条射线. ( )
(4)把线段向一个方向无限延伸可得到射线,向两个方向无限延伸可得到直线. ( )
√
√
√
×
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
直线、射线、线段的表示方法:
基本事实:
经过两点有一条直线,并且只有一条直线.
简单记为:两点确定一条直线.
(1)用一个小写英文字母表示;
(2)用两个大写字母表示.
直线
射线
线段
直线l或直线 AB(BA)
射线l或射线OA
线段 a或线段 AB(BA)
布置作业
教科书第129页 习题4.2
第1,2,3,4题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
4.2 直线、射线、线段
第 1 课时
学习目标
1. 了解线段、射线、直线的特征及表示方法.
2. 体会射线、直线的无限延伸,归纳线段、直线和射线三者之间的
联系与区别.
3. 通过直线、射线、线段概念的教学,培养学生的几何想象能力和
观察能力.
4. 培养学生对几何图形的兴趣,提高学习几何的积极性.
重点
直线
射线
线段
难点
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
请分别画出一条直线,一条射线和一条线段,然后说说
它们之间的联系与区别.
线段
射线
直线
复习回顾
区别:直线没有端点,射线有一个端点,线段有两个端点.
联系:都是直直的线.
(1) 经过一个点能画出几条直线?
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
结论:经过一个点能画出无数条直线.
合作探究
(2)经过两个点能画出几条直线呢?
基本事实:经过两点有一条直线,并且只有一条直线.
简单说成:两点确定一条直线.
下面两幅图的情形,在生活中很常见,你能说说它的原理吗?
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
交流
解:利用了两点确定一条直线的原理.
一般地,几何图形都有对应的符号语言表示,直线如何表示呢?
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
1.用一个小写的英文字母表示,如:直线l.
2.用直线上的两个点来表示,如:直线AB(或直线BA).
l
A B
合作探究
同时,也可以说点A、B在直线l上
l
结论:一个点在一条直线上,也可以说这条直线经过这个点.
一个点在一条直线外,也可以说这条直线不经过这个点.
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
下面两幅图中,你能描述一下点O和点P与直线l的位置关系吗?
点O在直线l上
或直线 l 经过点O
(1)
(2)
点P在直线l外
或直线 l 不经过点P
交流
下面的两幅图中分别能画出几条直线?
用数学语言描述图中点与直线PQ的位置关系.
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
(2)可以画出3条直线;
点O在直线PQ外,点P在直线PQ上,点Q在直线PQ上.
思考
P
Q
P
Q
解:(1)可以画出1条直线;
点O、P、Q三点共线,且都在直线PQ上
(1)
(2)
当两条不同的直线有一个公共点时,我们称这两条直线相交,这个公共点叫做它们的交点 .
应用新知
巩固新知
课堂小结
布置作业
探究新知
思考
创设情境
如图:直线a和直线b相交于点O.
点O叫做交点
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
线段a 线段AB 线段BA
a
A
B
射线l 射线OA(端点字母在前)
注意:用两个大写字母表示射线或线段.
(1)表示射线时,前一个字母表示射线的端点,
后一个字母表示射线上除端点外的任意一点.
(2)表示线段时,两个字母的顺序无特殊要求.
线段和射线都是直线的一部分,类比直线的表示方法,
线段和射线又如何表示呢?
图形
表示方法
探究
基本事实:
经过两点有一条直线,并且只有一条直线.
简单记为:两点确定一条直线.
归纳总结
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
直线、射线、线段的表示方法:
(1)用一个小写英文字母表示;
(2)用线上的两个点表示.
直线l或直线 AB(BA)
射线l或射线OA
线段 a或线段 AB(BA)
点与直线的位置关系:
(1)点在直线上(直线经过点);
(2)点在直线外(直线不经过点).
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例1 如左图,用一个钉子把一根细木条钉在墙上,木条能绕着钉子转动,这表明过一个点__________________;
如右图,用两个钉子把细木条钉在墙上,就能固定细木条,这表明 .
可以画无数条直线
两点确定一条直线
(1)
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例2 读下列语句,分别画出图形.
(1)直线AB经过点M ,点N在直线AB外;
(2)线段AB与线段CD相交于点O;
(3)射线OA.
例2 读下列语句,分别画出图形.
(1)直线AB经过点M ,点N在直线AB外;
(2)线段AB与线段CD相交于点O;
(3)射线OA.
(2)
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
D
C
O
例2 读下列语句,分别画出图形.
(1)直线AB经过点M ,点N在直线AB外;
(2)线段AB与线段CD相交于点O;
(3)射线OA.
(3)
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
判断下列说法是否正确,并说明理由.
(1)线段AB和射线AB都是直线AB的一部分. ( )
(2)直线AB和直线BA是同一条直线. ( )
(3)射线AB和射线BA是同一条射线. ( )
(4)把线段向一个方向无限延伸可得到射线,向两个方向无限延伸可得到直线. ( )
√
√
√
×
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
直线、射线、线段的表示方法:
基本事实:
经过两点有一条直线,并且只有一条直线.
简单记为:两点确定一条直线.
(1)用一个小写英文字母表示;
(2)用两个大写字母表示.
直线
射线
线段
直线l或直线 AB(BA)
射线l或射线OA
线段 a或线段 AB(BA)
布置作业
教科书第129页 习题4.2
第1,2,3,4题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
