2022-2023学年人教版八年级数学上册12.2 三角形全等的判定 (第2课时) 课件(共17张PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册12.2 三角形全等的判定 (第2课时) 课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 665.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 16:19:21 | ||
图片预览




文档简介
(共17张PPT)
12.2 三角形全等的判定
(第2课时)
人教版 数学 八年级 上册
3. 了解“SSA”不能作为两个三角形全等的条件.
1. 探索并正确理解三角形全等的判定定理“SAS”.
2. 会用“SAS”判定定理证明两个三角形全等并能应用其解决实际问题.
素养目标
1.回顾三角形全等的判定方法 1
三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”).
在△ABC和△ DEF中
∴ △ABC ≌△ DEF(SSS)
AB=DE,
BC=EF,
CA=FD,
2.符号语言表达:
A
B
C
D
E
F
温故知新
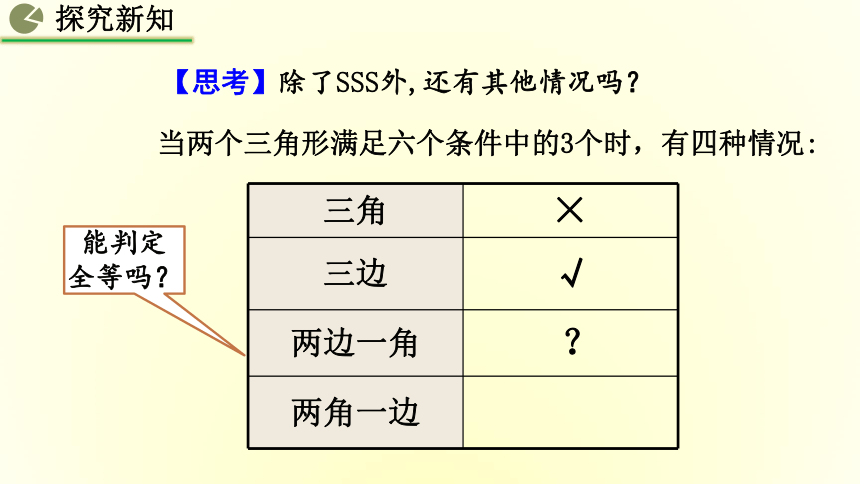
当两个三角形满足六个条件中的3个时,有四种情况:
三角 ×
三边 √
两边一角 ?
两角一边
【思考】除了SSS外,还有其他情况吗?
探究新知
能判定全等吗?
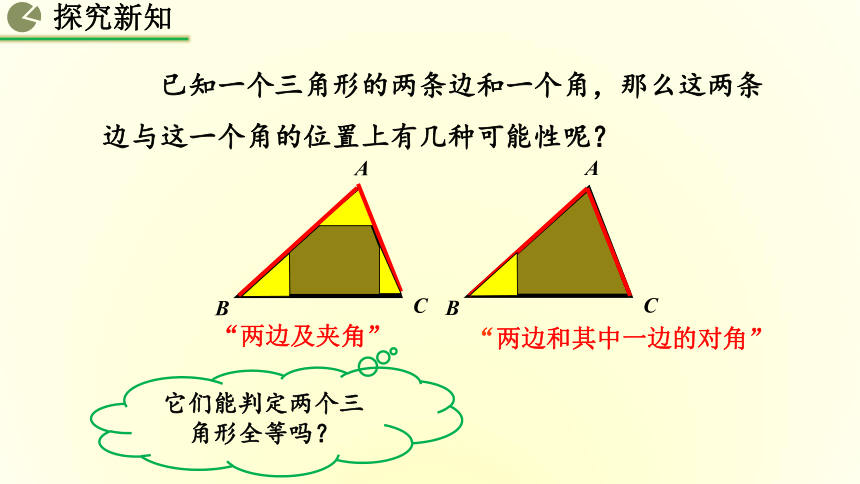
已知一个三角形的两条边和一个角,那么这两条边与这一个角的位置上有几种可能性呢?
A
B
C
A
B
C
“两边及夹角”
“两边和其中一边的对角”
它们能判定两个三角形全等吗?
探究新知
尺规作图画出一个△A′B′C′,使A′B′=AB,A′C′=AC,∠A′=∠A (即使两边和它们的夹角对应相等). 把画好的△A′B′C′剪下,放到△ABC上,它们全等吗?
A
B
C
两边及其夹角相等能否判定两个三角形全等
探究新知
做一做
A
B
C
A′
D
E
B′
C′
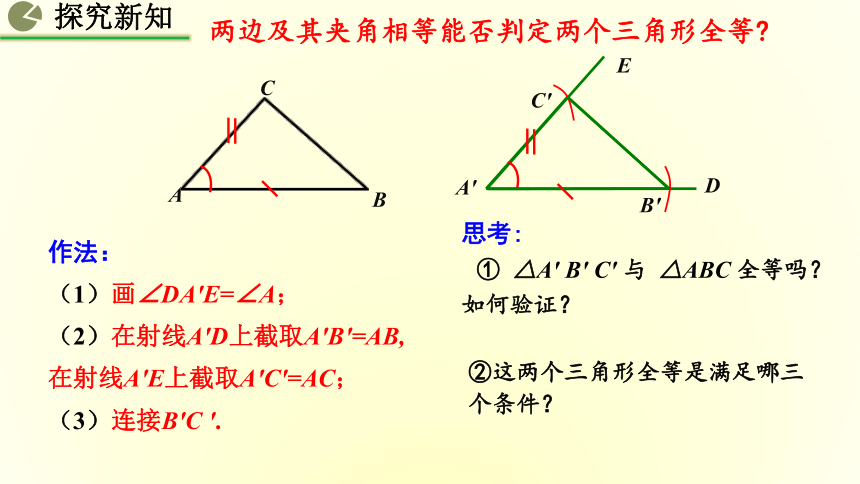
作法:
(1)画∠DA'E=∠A;
(2)在射线A'D上截取A'B'=AB,在射线A'E上截取A'C'=AC;
(3)连接B'C '.
思考:
① △A′ B′ C′ 与 △ABC 全等吗? 如何验证?
②这两个三角形全等是满足哪三个条件?
探究新知
两边及其夹角相等能否判定两个三角形全等
在△ABC 和△ DEF中,
∴ △ABC ≌△ DEF(SAS)
文字语言:
两边和它们的夹角分别相等的两个三角形全等.
(简写成“边角边”或“SAS ”).
几何语言:
CA = FD,
∠A =∠D,
AB =DE ,
A
B
C
D
E
F
必须是两边“夹角”
探究新知
知识点 1
三角形全等的判定——“边角边”定理
知识点1 运用“SAS”判定两个三角形全等
例1 如图2,O是AC,BD的交点,OA=OD,OB=OC.
求证:△OAB≌△ODC.
图2
证明:在△OAB和△ODC中
∴△OAB≌△ODC (SAS)
训练 1.如图3,已知OC平分∠MON,点A,B分别在射线OM,ON上,且OA=OB. 求证:△AOC≌△BOC.
图3
证明:∵OC平分∠MON
∴∠AOC=∠BOC
在△AOC和△BOC中,
∴△AOC≌△BOC (SAS)
例2 如图4,AB=AC,AD=AE,∠1=∠2.
求证:△ABD≌△ACE.
图4
证明:∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE
即∠BAD=∠CAE
在△ABD和△ACE中,
∴△ABD≌△ACE (SAS)
训练 2.如图5,已知OA=OC,OB=OD,∠AOC=∠BOD.
求证:△AOB≌△COD.
图5
证明:∵∠AOC=∠BOD,
∴∠AOC-∠AOD=∠BOD-∠AOD
即∠COD=∠AOB.
在△AOB和△COD中,
∴△AOB≌△COD (SAS)
知识点2 全等三角形(SAS)的判定与性质
例3 如图6,在△ABC中,D是边BC上的点,DE⊥AC,DF⊥AB,垂足分别为E,F,且DE=DF,CE=BF.求证:∠B=∠C.
图6
证明:∵DF⊥AB,DE⊥AC,
∴∠BFD=∠CED=90°
在△BDF和△CDE中,
∴△BDF≌△CDE (SAS)
∴∠B=∠C
训练 3.如图7,B,F,C,E四点在同一直线上,AB∥DE,AB=DE,BF=CE.求证:(1)△ABC≌△DEF;(2)AC∥DF.
图7
证明:(1)∵BF=CE
∴BF+FC=CE+FC
即BC=EF
∵AB∥DE ∴∠B=∠E
在△ABC与△DEF中,
∴△ABC≌△DEF (SAS)
(2)由(1),得△ABC≌△DEF
∴∠ACB=∠DFE
∴AC∥DF
(内错角相等,两直线平行)
易错点 “SSA”不能判定两个三角形全等
例4 如图8,已知△ABC的部分元素,在下面甲、乙、丙三个三角形中也标出了某些元素,则与△ABC不一定全等的三角形是________.(填“甲”或“乙”或“丙”)
图8
甲
乙
丙
甲
课堂归纳
1.在利用“两边一角对应相等”判定全等三角形时,角必须是两边的夹角.
2.通常利用已知条件得到角相等的情况:(1)对顶角的定义;(2)角平分线的定义;(3)角的和差;(4)垂直的定义;(5)平行线的性质等.
边角边
内容
有两边及夹角对应相等的两个三角形全等(简写成 “SAS”)
应用
为证明线段和角相等提供了新的证法
注意
1.已知两边,必须找“夹角”
2.已知一角和这角的一夹边,必须找这角的另一夹边
课堂小结
12.2 三角形全等的判定
(第2课时)
人教版 数学 八年级 上册
3. 了解“SSA”不能作为两个三角形全等的条件.
1. 探索并正确理解三角形全等的判定定理“SAS”.
2. 会用“SAS”判定定理证明两个三角形全等并能应用其解决实际问题.
素养目标
1.回顾三角形全等的判定方法 1
三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”).
在△ABC和△ DEF中
∴ △ABC ≌△ DEF(SSS)
AB=DE,
BC=EF,
CA=FD,
2.符号语言表达:
A
B
C
D
E
F
温故知新
当两个三角形满足六个条件中的3个时,有四种情况:
三角 ×
三边 √
两边一角 ?
两角一边
【思考】除了SSS外,还有其他情况吗?
探究新知
能判定全等吗?
已知一个三角形的两条边和一个角,那么这两条边与这一个角的位置上有几种可能性呢?
A
B
C
A
B
C
“两边及夹角”
“两边和其中一边的对角”
它们能判定两个三角形全等吗?
探究新知
尺规作图画出一个△A′B′C′,使A′B′=AB,A′C′=AC,∠A′=∠A (即使两边和它们的夹角对应相等). 把画好的△A′B′C′剪下,放到△ABC上,它们全等吗?
A
B
C
两边及其夹角相等能否判定两个三角形全等
探究新知
做一做
A
B
C
A′
D
E
B′
C′
作法:
(1)画∠DA'E=∠A;
(2)在射线A'D上截取A'B'=AB,在射线A'E上截取A'C'=AC;
(3)连接B'C '.
思考:
① △A′ B′ C′ 与 △ABC 全等吗? 如何验证?
②这两个三角形全等是满足哪三个条件?
探究新知
两边及其夹角相等能否判定两个三角形全等
在△ABC 和△ DEF中,
∴ △ABC ≌△ DEF(SAS)
文字语言:
两边和它们的夹角分别相等的两个三角形全等.
(简写成“边角边”或“SAS ”).
几何语言:
CA = FD,
∠A =∠D,
AB =DE ,
A
B
C
D
E
F
必须是两边“夹角”
探究新知
知识点 1
三角形全等的判定——“边角边”定理
知识点1 运用“SAS”判定两个三角形全等
例1 如图2,O是AC,BD的交点,OA=OD,OB=OC.
求证:△OAB≌△ODC.
图2
证明:在△OAB和△ODC中
∴△OAB≌△ODC (SAS)
训练 1.如图3,已知OC平分∠MON,点A,B分别在射线OM,ON上,且OA=OB. 求证:△AOC≌△BOC.
图3
证明:∵OC平分∠MON
∴∠AOC=∠BOC
在△AOC和△BOC中,
∴△AOC≌△BOC (SAS)
例2 如图4,AB=AC,AD=AE,∠1=∠2.
求证:△ABD≌△ACE.
图4
证明:∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE
即∠BAD=∠CAE
在△ABD和△ACE中,
∴△ABD≌△ACE (SAS)
训练 2.如图5,已知OA=OC,OB=OD,∠AOC=∠BOD.
求证:△AOB≌△COD.
图5
证明:∵∠AOC=∠BOD,
∴∠AOC-∠AOD=∠BOD-∠AOD
即∠COD=∠AOB.
在△AOB和△COD中,
∴△AOB≌△COD (SAS)
知识点2 全等三角形(SAS)的判定与性质
例3 如图6,在△ABC中,D是边BC上的点,DE⊥AC,DF⊥AB,垂足分别为E,F,且DE=DF,CE=BF.求证:∠B=∠C.
图6
证明:∵DF⊥AB,DE⊥AC,
∴∠BFD=∠CED=90°
在△BDF和△CDE中,
∴△BDF≌△CDE (SAS)
∴∠B=∠C
训练 3.如图7,B,F,C,E四点在同一直线上,AB∥DE,AB=DE,BF=CE.求证:(1)△ABC≌△DEF;(2)AC∥DF.
图7
证明:(1)∵BF=CE
∴BF+FC=CE+FC
即BC=EF
∵AB∥DE ∴∠B=∠E
在△ABC与△DEF中,
∴△ABC≌△DEF (SAS)
(2)由(1),得△ABC≌△DEF
∴∠ACB=∠DFE
∴AC∥DF
(内错角相等,两直线平行)
易错点 “SSA”不能判定两个三角形全等
例4 如图8,已知△ABC的部分元素,在下面甲、乙、丙三个三角形中也标出了某些元素,则与△ABC不一定全等的三角形是________.(填“甲”或“乙”或“丙”)
图8
甲
乙
丙
甲
课堂归纳
1.在利用“两边一角对应相等”判定全等三角形时,角必须是两边的夹角.
2.通常利用已知条件得到角相等的情况:(1)对顶角的定义;(2)角平分线的定义;(3)角的和差;(4)垂直的定义;(5)平行线的性质等.
边角边
内容
有两边及夹角对应相等的两个三角形全等(简写成 “SAS”)
应用
为证明线段和角相等提供了新的证法
注意
1.已知两边,必须找“夹角”
2.已知一角和这角的一夹边,必须找这角的另一夹边
课堂小结
