2022—2023学年沪教版(五四制)数学七年级上册10.1分式的意义 课件 (共13张PPT)
文档属性
| 名称 | 2022—2023学年沪教版(五四制)数学七年级上册10.1分式的意义 课件 (共13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 222.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 16:30:57 | ||
图片预览




文档简介
(共13张PPT)
分式的意义
1、(1)学校有两块面积分别为230平方米与 a平方米的空地,现打算分别种上不同的花卉.若用3万元投资在230平方米的空地上,用x万元投资在a平方米的空地上.那么每平方米的花卉价格分别为多少万元?
(2)后因考虑到实际效果,改为在230平方米的空地上投资x万元,在a平方米的空地上投资3万元.那么每平方米的花卉价格分别为多少万元?两块地花卉的平均价格为多少万元?
用代数式表示下列问题中所要求的量:
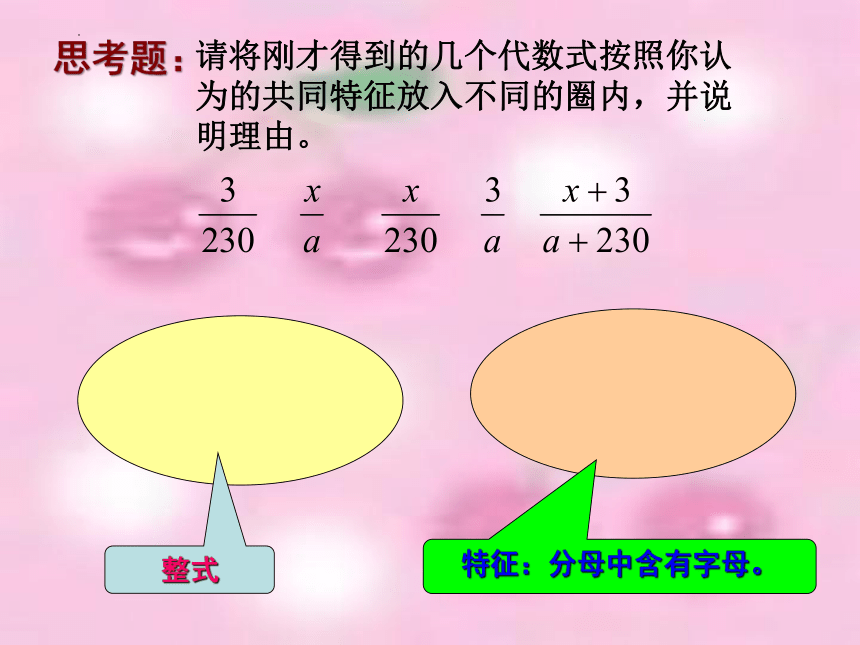
请将刚才得到的几个代数式按照你认为的共同特征放入不同的圈内,并说明理由。
思考题:
特征:分母中含有字母。
整式
两个整式A、B相除,即A÷B时,可以表示为 。如果B中含有字母, 那么 叫做分式。A叫做分式的分子,B叫做分式的分母。
分式的概念:
练习:下列代数式中,哪些是整式?哪些是分式?
整式:{ …}
分式:{ …}
两个整式A、B相除,即A÷B时,可以表示为 。如果B中含有字母, 那么 叫做分式。A叫做分式的分子,B叫做分式的分母。
分式的概念:
思考:
两个整式A、B相除叫做分式,对吗?请举例说明。
如果B是非零常数,那么 是分式。
如果一个分式的分母为零,那么这个分式无意义。
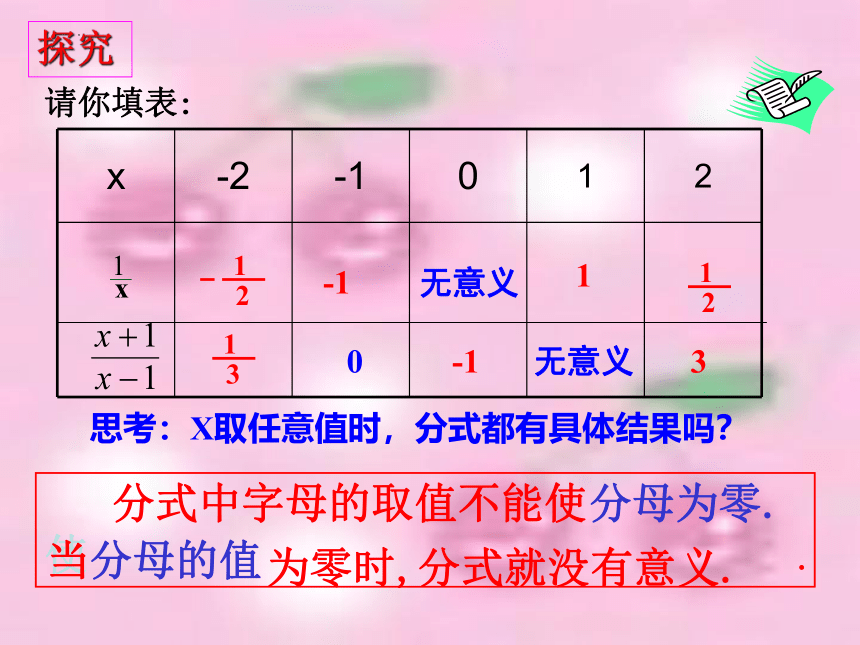
探究
x -2 -1 0 1 2
请你填表:
1
x
思考:X取任意值时,分式都有具体结果吗?
1
2
-1
1
1
2
1
3
-1
3
无意义
0
无意义
分式中字母的取值不能使使 .
分母为零.
当分母的值
为零时,分式就没有意义.
例1、当x取什么值时,下列分式无意义?
变式训练:
(1)当x取什么值时,分式 有意义。
(2)当x取什么值时,分式 有意义。
例题分析:
如果分母为零,那么分式无意义。
如果分母不为零,那么分式有意义。
例2、当y是什么值时,分式 的值是0?
分析:分式的值为0需满足的条件是分子的值为0且分母的值不为0。
例题分析:
变式训练:
(1)当y是什么值时,分式 的值是0?
(2)当y是什么值时,分式 的值是正数?
用心填一填
(1)当__________时,分式 有意义;
(2)当___________时,分式 无意义;
(3)当___________时,分式 的值为零;
(4)当______________时,分式 的值为零;
(5)当________________ 时,分式 有意义;
x≠0
x=2
x=3
x≠-1且x≠ 2
x= -1
当 _____________ 时,分式
x=-1或x= 2
无意义;
选择:
1.使分式 有意义的 值必为 ( )
A B C D 任意有理数
B
分析:
分母
得
2.当 时,分式① ②
③ ④ 无意义的是
A ①② B ②③ C ①③ D ②④
( )
C
判断:
1、对于任意有理数 ,分式 有意义 ( )
2、若分式 无意义,则 的值一定是-3 ( )
√
×
则
无论 取何值,
分析
课堂小结
同学们,再见!
分式的意义
1、(1)学校有两块面积分别为230平方米与 a平方米的空地,现打算分别种上不同的花卉.若用3万元投资在230平方米的空地上,用x万元投资在a平方米的空地上.那么每平方米的花卉价格分别为多少万元?
(2)后因考虑到实际效果,改为在230平方米的空地上投资x万元,在a平方米的空地上投资3万元.那么每平方米的花卉价格分别为多少万元?两块地花卉的平均价格为多少万元?
用代数式表示下列问题中所要求的量:
请将刚才得到的几个代数式按照你认为的共同特征放入不同的圈内,并说明理由。
思考题:
特征:分母中含有字母。
整式
两个整式A、B相除,即A÷B时,可以表示为 。如果B中含有字母, 那么 叫做分式。A叫做分式的分子,B叫做分式的分母。
分式的概念:
练习:下列代数式中,哪些是整式?哪些是分式?
整式:{ …}
分式:{ …}
两个整式A、B相除,即A÷B时,可以表示为 。如果B中含有字母, 那么 叫做分式。A叫做分式的分子,B叫做分式的分母。
分式的概念:
思考:
两个整式A、B相除叫做分式,对吗?请举例说明。
如果B是非零常数,那么 是分式。
如果一个分式的分母为零,那么这个分式无意义。
探究
x -2 -1 0 1 2
请你填表:
1
x
思考:X取任意值时,分式都有具体结果吗?
1
2
-1
1
1
2
1
3
-1
3
无意义
0
无意义
分式中字母的取值不能使使 .
分母为零.
当分母的值
为零时,分式就没有意义.
例1、当x取什么值时,下列分式无意义?
变式训练:
(1)当x取什么值时,分式 有意义。
(2)当x取什么值时,分式 有意义。
例题分析:
如果分母为零,那么分式无意义。
如果分母不为零,那么分式有意义。
例2、当y是什么值时,分式 的值是0?
分析:分式的值为0需满足的条件是分子的值为0且分母的值不为0。
例题分析:
变式训练:
(1)当y是什么值时,分式 的值是0?
(2)当y是什么值时,分式 的值是正数?
用心填一填
(1)当__________时,分式 有意义;
(2)当___________时,分式 无意义;
(3)当___________时,分式 的值为零;
(4)当______________时,分式 的值为零;
(5)当________________ 时,分式 有意义;
x≠0
x=2
x=3
x≠-1且x≠ 2
x= -1
当 _____________ 时,分式
x=-1或x= 2
无意义;
选择:
1.使分式 有意义的 值必为 ( )
A B C D 任意有理数
B
分析:
分母
得
2.当 时,分式① ②
③ ④ 无意义的是
A ①② B ②③ C ①③ D ②④
( )
C
判断:
1、对于任意有理数 ,分式 有意义 ( )
2、若分式 无意义,则 的值一定是-3 ( )
√
×
则
无论 取何值,
分析
课堂小结
同学们,再见!
