2022—2023学年沪教版(五四制)数学七年级上册10.6整数指数幂(2) 课件 (共21张PPT)
文档属性
| 名称 | 2022—2023学年沪教版(五四制)数学七年级上册10.6整数指数幂(2) 课件 (共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 674.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 16:32:32 | ||
图片预览



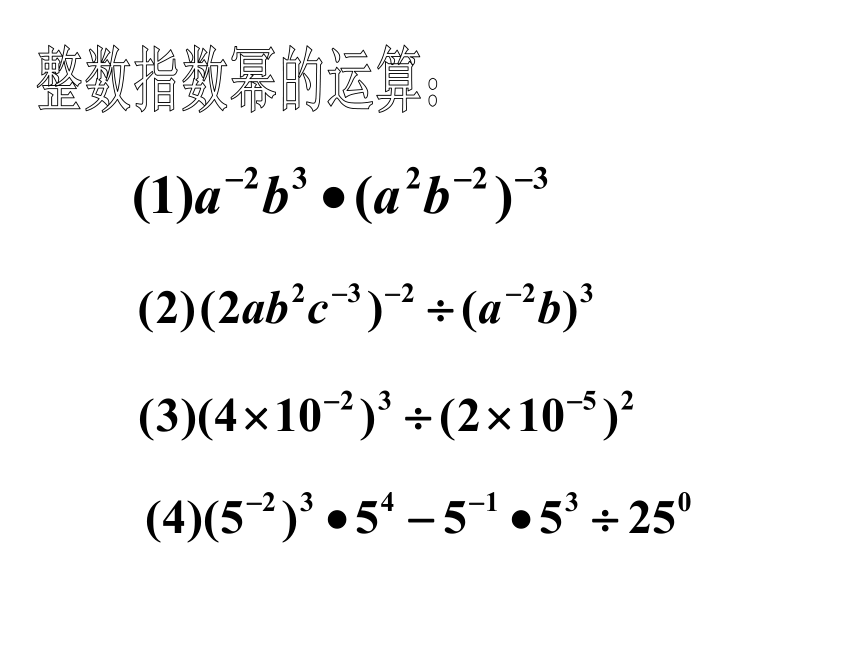




文档简介
(共21张PPT)
第十六章 分式
10.6 整数指数幂(2)
复习回顾
例1:计算
(1) (3m-2n-1)-3
(2) 2a-2 b2 ÷(2a-1 b-2)-3
整数指数幂的运算:
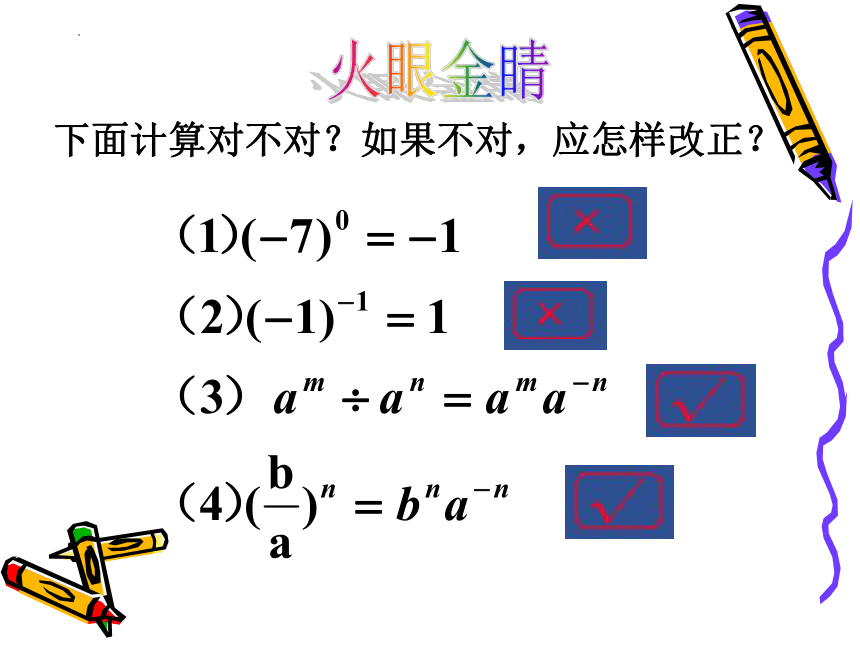
火眼金睛
下面计算对不对?如果不对,应怎样改正?
2、如何用科学记数法表示一个数?
一个数M的绝对值大于1,这个数M可表示为
形式,其中 ,n为正整数,
n是原数的整数位数减1。
1、科学计数法:
光速约为300 000 000米/秒
太阳半径约为696 000千米
目前世界人口约为6 100 000 000
3×108
6.96×105
6.1×109
3、用科学记数法表示下列各数:
300000 =_______, -5230000=_______,
12600=_________.
一般地, 10-n =_____
自主探究
填空:
1
0.1
0.01
0.001
0.000 1
( n 等于第一个非0数前面所有0 的个数)
尝试:我们已经知道一些绝对值较大的数适合用科学记数
法表示,例如: ;
你能利用10的负整数指数幂,将绝对值较小的数表示成
类似形式吗?
0.01= ;
0.000 001= ;
0.000 0257= = ;
0.000 000 125= ,
= ;
归纳
绝对值小于1的数可以用科学记数法表示为
的形式,其中a是整数数位只
有一位的数,n是正整数,n等于这个数从左边第一个不是零的数字算起前面零的个数(包括小数点前面的零)。
例1:用科学记数法表示下列各数:
(1). -0.00060
(2). 0.00007283(保留两个有效数字)
(3). 0.00618
(4) -0.00258(精确到万分位)
例2:用整数或小数表示下列各数:
=203 000
=0.00 786
=-0.000 005 5
尝试1:用科学记数法表示下列各数
(1)0.000 000 001
(2)0.001 2
(3)0.000 000 345(保留两个有效数字)
(4)-0.000 03
(5)0.000 000 010 8
尝试2:下列用科学计数法表示的数,原数是多少
5
例 纳米是非常小的长度单位,1纳米= 米。
把1纳米的物体放在乒乓球上,就如同把乒乓球
放到地球上。1立方毫米的空间可以放多少个
1立方纳米的物体?
例 计算
巩固练习
其中正确的有( )
A、 1个 B、2个 C、3个 D、4个
B
3
4、先化简再求值
其中x=-2,y=-3
思考题:
小
结
(1)n是正整数时, a-n属于分式。并且
(a≠0)
(2)科学计数法表示小于1的小数:
a×10-n
(a 是整数位只有一位的正数,n是正整数。)
思考1:
1、当x为何值时,有意义?
2、当x为何值时,无意义?
3、当x为何值时,值为零?
4、当X为何值时,值为正?
课堂达标测试
基础题:
1.计算:
(a+b)m+1·(a+b)n-1; (2) (-a2b)2·(-a2b3)3÷(-ab4)5
(3) (x3)2÷(x2)4·x0
(4) (-1.8x4y2z3) ÷(-0.2x2y4z) ÷(-1/3xyz)
提高题:
2.已知 ,求a51÷a8的值;
3.计算:xn+2·xn-2÷(x2)3n-3;
4.已知:10m=5,10n=4,求102m-3n.
思考2:
5.探索规律:31=3,个位数字是3;32=9,个位数字式9;33=27,个位数字是7;34=81,个位数字是1;35=243,个位数字是3;36=729,个位数字是9;……那么,37的个位数字是______,320的个位数字是______。
兴趣探索
第十六章 分式
10.6 整数指数幂(2)
复习回顾
例1:计算
(1) (3m-2n-1)-3
(2) 2a-2 b2 ÷(2a-1 b-2)-3
整数指数幂的运算:
火眼金睛
下面计算对不对?如果不对,应怎样改正?
2、如何用科学记数法表示一个数?
一个数M的绝对值大于1,这个数M可表示为
形式,其中 ,n为正整数,
n是原数的整数位数减1。
1、科学计数法:
光速约为300 000 000米/秒
太阳半径约为696 000千米
目前世界人口约为6 100 000 000
3×108
6.96×105
6.1×109
3、用科学记数法表示下列各数:
300000 =_______, -5230000=_______,
12600=_________.
一般地, 10-n =_____
自主探究
填空:
1
0.1
0.01
0.001
0.000 1
( n 等于第一个非0数前面所有0 的个数)
尝试:我们已经知道一些绝对值较大的数适合用科学记数
法表示,例如: ;
你能利用10的负整数指数幂,将绝对值较小的数表示成
类似形式吗?
0.01= ;
0.000 001= ;
0.000 0257= = ;
0.000 000 125= ,
= ;
归纳
绝对值小于1的数可以用科学记数法表示为
的形式,其中a是整数数位只
有一位的数,n是正整数,n等于这个数从左边第一个不是零的数字算起前面零的个数(包括小数点前面的零)。
例1:用科学记数法表示下列各数:
(1). -0.00060
(2). 0.00007283(保留两个有效数字)
(3). 0.00618
(4) -0.00258(精确到万分位)
例2:用整数或小数表示下列各数:
=203 000
=0.00 786
=-0.000 005 5
尝试1:用科学记数法表示下列各数
(1)0.000 000 001
(2)0.001 2
(3)0.000 000 345(保留两个有效数字)
(4)-0.000 03
(5)0.000 000 010 8
尝试2:下列用科学计数法表示的数,原数是多少
5
例 纳米是非常小的长度单位,1纳米= 米。
把1纳米的物体放在乒乓球上,就如同把乒乓球
放到地球上。1立方毫米的空间可以放多少个
1立方纳米的物体?
例 计算
巩固练习
其中正确的有( )
A、 1个 B、2个 C、3个 D、4个
B
3
4、先化简再求值
其中x=-2,y=-3
思考题:
小
结
(1)n是正整数时, a-n属于分式。并且
(a≠0)
(2)科学计数法表示小于1的小数:
a×10-n
(a 是整数位只有一位的正数,n是正整数。)
思考1:
1、当x为何值时,有意义?
2、当x为何值时,无意义?
3、当x为何值时,值为零?
4、当X为何值时,值为正?
课堂达标测试
基础题:
1.计算:
(a+b)m+1·(a+b)n-1; (2) (-a2b)2·(-a2b3)3÷(-ab4)5
(3) (x3)2÷(x2)4·x0
(4) (-1.8x4y2z3) ÷(-0.2x2y4z) ÷(-1/3xyz)
提高题:
2.已知 ,求a51÷a8的值;
3.计算:xn+2·xn-2÷(x2)3n-3;
4.已知:10m=5,10n=4,求102m-3n.
思考2:
5.探索规律:31=3,个位数字是3;32=9,个位数字式9;33=27,个位数字是7;34=81,个位数字是1;35=243,个位数字是3;36=729,个位数字是9;……那么,37的个位数字是______,320的个位数字是______。
兴趣探索
