中考数学复习之几何经典练习题(PDF版 含答案)
文档属性
| 名称 | 中考数学复习之几何经典练习题(PDF版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 16:46:32 | ||
图片预览


文档简介
中考复习几何经典练习题
1.如图,a||b||c,直线 a与直线 b之间的距离为,直线 c与直线 b之间的距离为,等边 ABC
的三个顶点分别在直线 a、b、c上,则等边 ABC的边长为________
2.如图,正方形 ABCD中,E为 BC中点,连接 AE,DF⊥AE于点 F,连接 CF,FG⊥CF
AF 2
交 AD于点 G,下列结论:①CF=CD;②G为 AD中点;③△DCF∽△AGF;④ ,
EF 3
其中结论正确的是__________
3.如图,在矩形 ABCD中,AB= 3,AD=3;连接 BD,O是 BD中点,点 G由 A出发以
每秒一个单位向 D运动,连接 OG,直线 OG交 BC于 F,过 A作 AE⊥GF于 E,连接
DE,设运动时间为 t(0<t<3),则以下结论正确的是____________.
①当且仅当 t=1时,△DFG为等边三角形;②当且仅当 t=1 时,△AEG和△BCD相
3 3 21 3
似;③当 t= 时,CF= 2 AE;④在运动的过程中,DE有最小值为 .
2 4
4.如图,在 Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,P是 AE边上一点,
PC 3 CK
连结 PC并延长交 HI于点 Q,连结 CG交 AB于点 K.若 ,则
CQ 4 KG _________
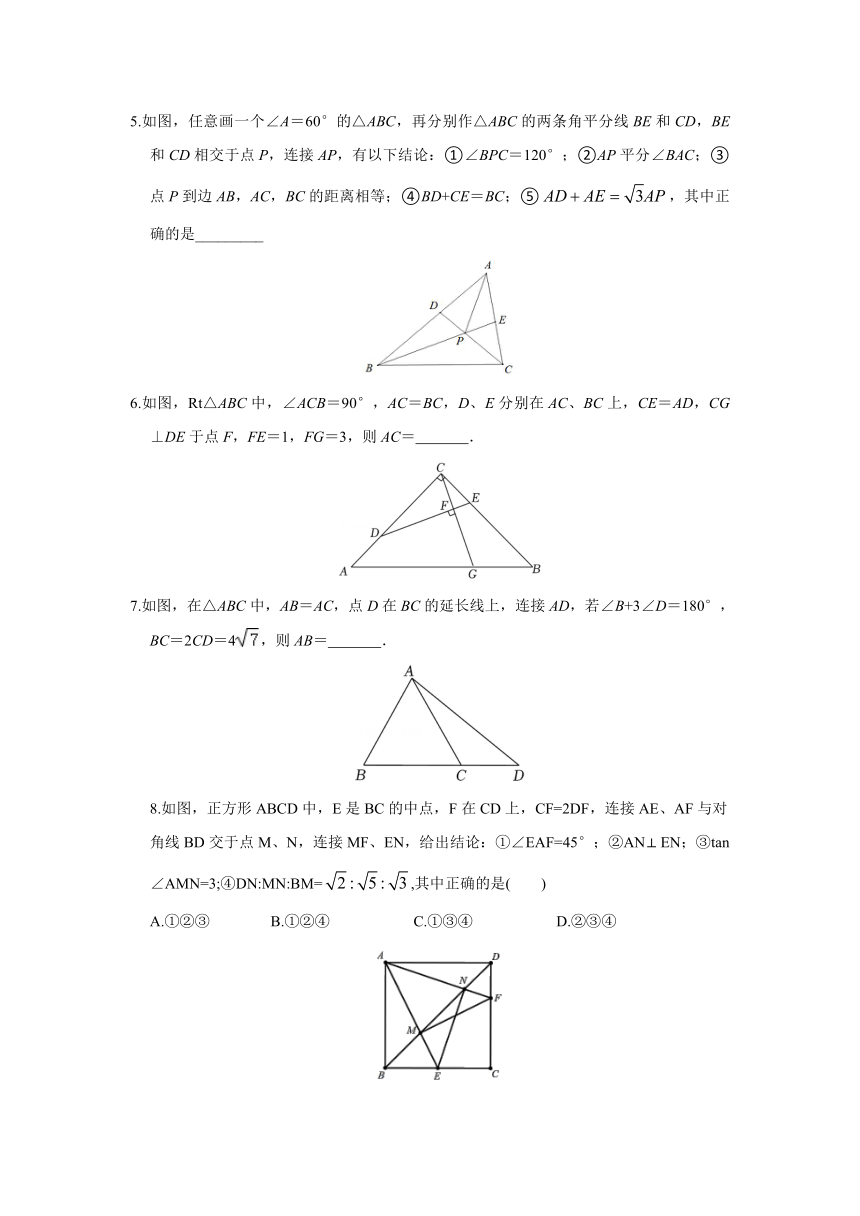
5.如图,任意画一个∠A=60°的△ABC,再分别作△ABC的两条角平分线 BE和 CD,BE
和 CD相交于点 P,连接 AP,有以下结论:①∠BPC=120°;②AP平分∠BAC;③
点 P到边 AB,AC,BC的距离相等;④BD+CE=BC;⑤ AD AE 3AP,其中正
确的是_________
6.如图,Rt△ABC中,∠ACB=90°,AC=BC,D、E分别在 AC、BC上,CE=AD,CG
⊥DE于点 F,FE=1,FG=3,则 AC= .
7.如图,在△ABC中,AB=AC,点 D在 BC的延长线上,连接 AD,若∠B+3∠D=180°,
BC=2CD=4 ,则 AB= .
8.如图,正方形 ABCD中,E是 BC的中点,F在 CD上,CF=2DF,连接 AE、AF与对
角线 BD交于点M、N,连接MF、EN,给出结论:①∠EAF=45°;②AN EN;③tan
∠AMN=3;④DN:MN:BM= 2 : 5 : 3 ,其中正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
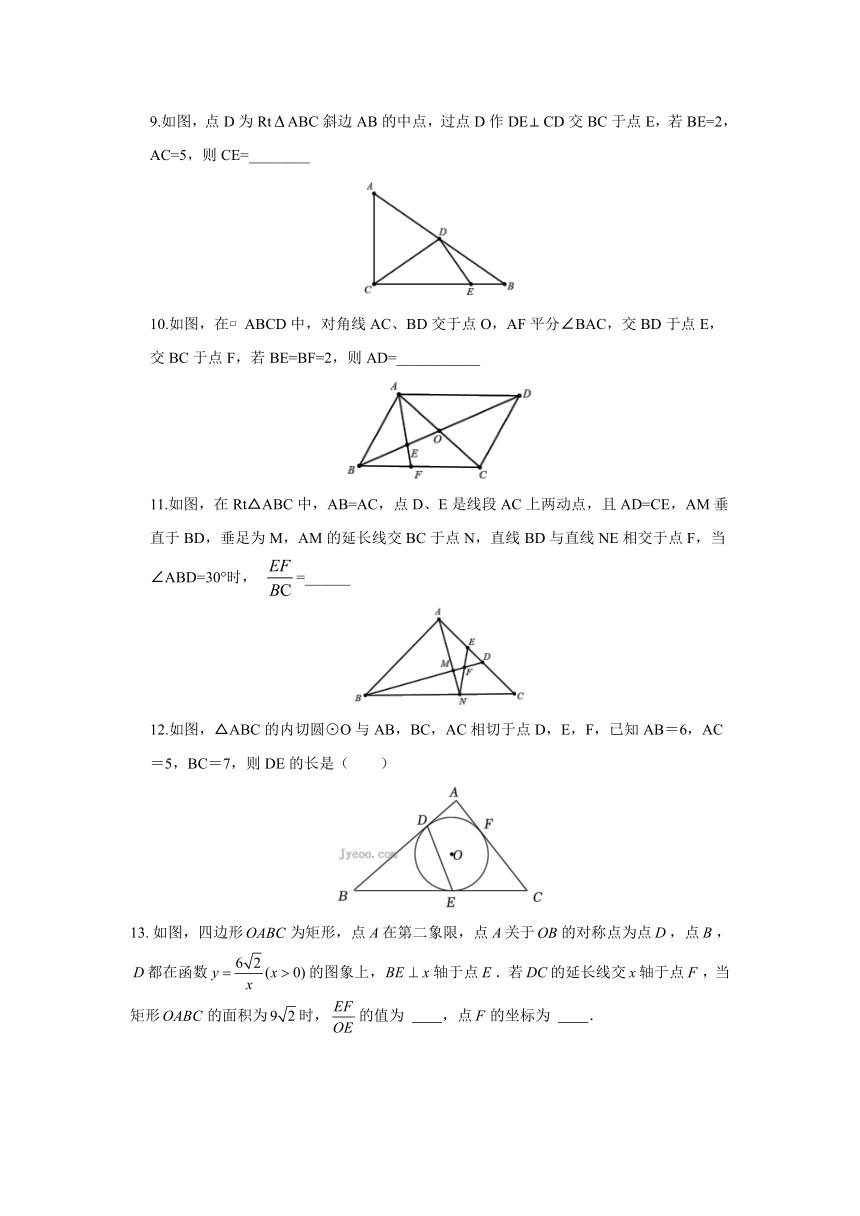
9.如图,点 D为 Rt ABC斜边 AB的中点,过点 D作 DE CD交 BC于点 E,若 BE=2,
AC=5,则 CE=________
10.如图,在 ABCD中,对角线 AC、BD交于点 O,AF平分∠BAC,交 BD于点 E,
交 BC于点 F,若 BE=BF=2,则 AD=___________
11.如图,在 Rt△ABC中,AB=AC,点 D、E是线段 AC上两动点,且 AD=CE,AM垂
直于 BD,垂足为M,AM的延长线交 BC于点 N,直线 BD与直线 NE相交于点 F,当
EF
∠ABD=30°时, =______
BC
12.如图,△ABC的内切圆⊙O与 AB,BC,AC相切于点 D,E,F,已知 AB=6,AC
=5,BC=7,则 DE的长是( )
13.如图,四边形OABC 为矩形,点 A在第二象限,点 A关于OB的对称点为点D,点 B,
D 6 2都在函数 y (x 0)的图象上,BE x轴于点 E.若DC的延长线交 x轴于点 F ,当
x
矩形OABC 9 2 EF的面积为 时, 的值为 ,点 F 的坐标为 .
OE
3
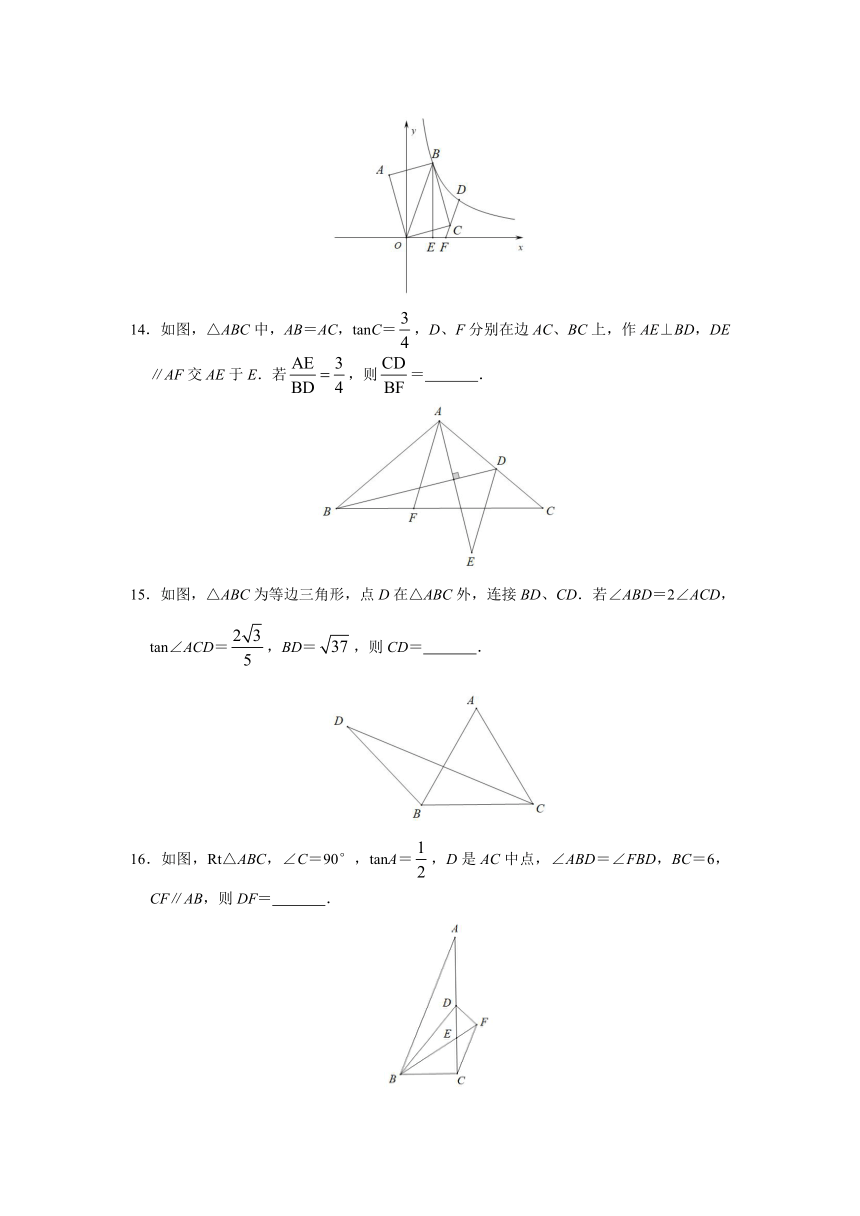
14.如图,△ABC中,AB=AC,tanC= ,D、F分别在边 AC、BC上,作 AE⊥BD,DE
4
AE 3 CD
∥AF交 AE于 E.若 ,则 = .
BD 4 BF
15.如图,△ABC为等边三角形,点 D在△ABC外,连接 BD、CD.若∠ABD=2∠ACD,
2 3
tan∠ACD= ,BD= 37 ,则 CD= .
5
1
16.如图,Rt△ABC,∠C=90°,tanA= ,D是 AC中点,∠ABD=∠FBD,BC=6,
2
CF∥AB,则 DF= .
17.如图,已知 AB=CD,BC=2AD,∠ABC=90°,∠BCD=30°,则∠BAD=______
18.点 E是平行四边形 ABCD的边 AD的中点,AB AC,BE CE,则 tan∠DFE=_____
19.如图,点E、F在正方形ABCD边上,AE与CF交于点G,若AG=BC= 3 1,∠CGE=45°,
则 CF=____
20.如图,四边形 ABCD中,∠BAD=∠BCD=45°,AB=4 2 ,CD=5,AD=7,则 AC=_______
1
21.如图所示,ABCD为正方形,ADEF为矩形,∠AMB= ∠AED,若 AN=2,ME=3,则
2
DN=______
22.已知点 A(0,2),点 B在 x轴正半轴上,将 AB绕点 A逆时针旋转 60°至 AC,点 C(m,3),则
m=____
23.如图,矩形 ABCD中,AB=5,BC=4,点 E是 AB边上一点,AE=3,连接 DE,点 F是
1
BC延长线上一点,连接 AF,且∠F= ∠EDC,则 CF=_______
2
24.如图,正方形 ABCD的对角线 AC上有一点 E,且 CE=4AE,点 F在 DC的延长线上,
连接 EF,过点 E作 EG EF,交 CB的延长线于点 G,连接 GF并延长,交 AC延长线于点
P,若 AB=5,CF=2,则线段 EP的长是________
25.如图,已知⊙O的半径为 1,AB、AC是⊙O的两条弦,且 AB=AC,延长 BO交 AC于
点 D,若 AD2=AB DC,则 OD=______
26.如图,AB和 BC是⊙O的两条弦(即 ABC是圆的一条折弦),BC>AB,M是弧 ABC的中
点,则从M向 BC所作垂线的垂足 D是折弦 ABC的中点,若 AB=2 2 ,BD= 2 ,则
CD=_______
27.如图, ABC是圆 O的内接三角形,弦 EF过 BC的中点 D,且 EF||AB,若 AB=4,则
DE的长为__________
28.如图, ABC内接于圆 O,过 BC的中点 D作直线 l||AC,l与 AB交于点 E,与圆 O交
于点 G、F,与圆 O在点 A处的切线交于点 P,若 PE=3,DE=2,EF=3,则 PA的长为_________
29.已知 P为 ABC内一点,满足∠BAP=20°,∠CAP=28°,∠ACP=48°,AP=BC,则
∠BCP=______
30.如图,在 ABC中,AB=12,BC=10, ABC的内心、外心分别为点 I、O,且有 OI⊥
AI,则 AC=______
中考数学真题经典(十)参考答案
1.解:如图所示,在直线 c上取点 D、E,使∠BDC=∠AEC=60°,易知△BCD △CAE,
AE=CD作 BG⊥c,AH⊥c于 G、H,BG=2 3,AH=3 3,DG=2,BD=4,故 CG=4,HE=3,
AE=6,得 BC=2 7
2. 解:延长 AE交 DC延长线于点 H,易知△ABE △HCE,CH=AB,故 C为 DH的中点,
故 CF=CD,正确;由 CF=CD得∠CFD=∠CDF,故∠GFD=∠GDF,DF=GD而∠DAF+∠
ADF=∠AFG+∠DFG=90,得∠GAF=∠GFA,故 AG=GF,故 AG=DG,G为 AD的中点;
由∠GAF=∠CDF,故△DCF~△AGF;tan∠DAF=2,得 DF=2AF,FH=2DF,故 FH=4AF,
AF:EF=2:3;故①①③正确.
3. 解:当 t=1时,∠CDF=30°,∠FDG=60°,DF=2,而 AG=CF=1,故 DG=2,△DFG
为等边三角形;t=2 时,△AEG与△BCD相似,故错误;AG=CF,当 CF= 2 AE时有∠
3 3 3
AGE=45°,OH=GH= ,故 t=AG= ;点∠AEO=90°,点 E在以 AO为直径的圆
2 2
21 3
上运动,当 H、E、D共线时,DE取最小值,最小值为 ,故①正确.
2
4.解:作 CM⊥AB于点M,易知△ACP~△ICQ得 AC:CI=3:4,设 AC=3,则 BC=4,AB=5,
12
得 CM= ,CM||BG,CM:KG=CM:BG=12:25
5
5.解:由角平分线的性质可知∠BPC=90°+∠BAC,而∠BAC=60°,故∠BPC=120°,①正确;
三角形内角平分线交于一点,故 PA平分∠BAC,②③正确;在 BC上截取一点 F使 BF=BD,
易知△BPD △BPF和△CPF △CPE,④正确;作 PM⊥AB,PN⊥AC,易得
△PDM △PEN,AD+AE=2AM=AP,故①②③④⑤正确.
6. 作 DH⊥AD交 AB于点 H,连接 CH、EH,得 AD=DH,而 AD=CE,故 DH=CE,故 CDHE
为矩形;同时∠ECF=∠CDE=∠ACH,∠CHG=∠A+∠ACH,∠CGH=∠B+∠BCG,故
∠CHG=∠CGH,故 CG=CH;设 CF=x,则 DE=x+3,DF=x+2,由射影定理知 CF2=EF DF得
x2=(x+2),x=2,故 CE= 5,CD=2 5,故 AC=3 5
7.解:在 AD上取一点M使MC=MD,设∠D=α,则∠AMC=∠ACM=2α,则 AM=AC,设
AB=3x,则MD=x,AD2-DH2=AC2-CH2,得 (4x)2 (4 7)2 (3x)2 (2 7)2,x=2 3 ,AB=6 3
1 1
8.解:由 tan∠DAF= ,tan∠BAE= ,得∠DAF+∠BAE=45°,故∠EAF=45°;
3 2
∠EAF=∠MBE=45°,故 A、B、E、M共圆,故∠AEN=∠ABN=45°,故 AN⊥NE;
∠AMN=∠AFD,故 tan∠AMN=3;易知△ADN~△ACE,设 AB=8,则 CE=4,DN=2 2 ;
△ABM~△ACF,CF=6,则 BM=3 2 ,故正确的为①②③,选 A.
9.延长 CD至点 F使 DF=CD,连接 BF,易证△ACD △BDF,∠DBF=∠A,得∠CBF=90°,
BF=AC=5,而 CD=DF,ED⊥CF故 EF=CE= 29
10.解:
方向一:等腰三角形
解:易知 ADE亦为等腰三角形,设∠OAE=ɑ,∠OAD=β,则∠BAF=ɑ,∠AEO=ɑ+β,故∠
x 2
x 2 OD AD
ABD=β,故 DAO~ DBA,设 AD=x,则 OD= ,而 ,故 2 x ,
2 AD BD x x 2
x=2+2 2
点评:由等腰三角形得到一系列角度关系,通过角度关系得到相似三角形.这个突破点属于
比较常规的,当不知如何解答时,推导角度关系明显不失为一种很好的方式.
另法:角平分线定理
由角度关系可得比较多的相似三角形,易知相似比为 2 .
AB AO
解: ABO~ ACB, 得AB2 2OA2 即有AB 2OA ,由角平分线定理知
AC AB
AB BF
,故 CF=2 2 ,AD=2+2 2
AC CF
(亦可由 ABE~ ACF AB AO BO 2求得 CF的长度)此结论 可作为后续解法的基
AC AB BC 2
本结论.
方向二:角平分线
由角平分线可以联想到角平分线的性质、对称图形、全等三角形,因为题目本身呈现出好几
个等腰三角形,更易往全等三角形的方向联想.通过辅助线,构造全等三角形解决线段长问
题.
解法 1:在 AB延长线上取一点 G,使 AG=AC,易知 AFG AFC,∠AGF=∠ACF,而
AB BE
∠ABE=∠ACB,故∠ABE=∠AGF,得 BE||GF, 得 GF=2 2 ,故 AD=2+2AG GF 2
解法 2:在 AC 上取一点 G,使 AG=AB,易知 ABF AGF,∠AFG=∠AFB,而
GF CF
∠AFB=∠BEF,故∠AEO=∠AFG BE||GF OB 2,得 , ,而 得 CF=2
OB BC 2BC 2
解法 3:延长 CA至点 G,使 AG=AB,易知 AF||BG AG BF 2, ,得 CF=2 2 ,故
AC CF 2
AD=2+2 2
4 BA H AH=AC AF||CH AB BF 2解法 :延长 至点 ,使 ,易知 , ,得 CF=2 2 ,故
AH CF 2
AD=2+2 2
方向三:由中点构造中位线、平行线
解法 5:过点 O 作 OH||BC AO OE 2, 得 OE= 2 ,而 OH=OE,故 CF=2 2 ,
AB BE 2
AD=2+2 2
6 C CG||OB AO OE 2解法 :过点 作 , 得 OE= 2 ,而 CH=CG,故 CF=2 2 ,
AB BE 2
AD=2+2 2
AB OB
解法 7:过点 O 作 OG||AB,易知 ABO~ OCG, ,CG= 2 +1,故OC CG
AD=BC=2+2 2
解法 8:过点 E作 EG||BC,易知 ABE AGE AG EG 2, ,EG= 2 ,CF=2 2 ,
AC CF 2
故 AD=2+2 2
解法 9:过点 C作 CG||AF,易知 AOE COG,易知 BCG为等腰三角形,EG=CF,而
OE=OG= 2 ,故 CF=2 2 ,AD=2+2 2
解法 10:作 BM AF,CN AF BM AB 2,易知 ABM~ ACN, ,而 BMF~ CNF,
CN AC 2
BF BM
,故 CF=2 2 ,AD=2+2CF CN 2
11. 解:过点 C作 CG AC交 AN延长线于点 G,AB=AC,∠ABD=∠CAG=30°,
∠BAD=∠ACG,故△ABD≌△CAG,CG=AD,而 AD=CE,故 CG=CE;CN=CN,NCE=NCG,
故△CNE≌△CNG;∠CEN=60°,故△EFD为等边三角形,设 NG=2a,则 GC=( 3 1)a,
AC=(3 3 EF 2 6 3 2)a,EF=( 3 1)a,BC=( 6 3 2 )a,故
BC 6
12.解:连接 OD、OE、OF,设 AF=x,则 AD=x,CE=CF=5-x,BE=BD=6-x,故 6-x+5-x=7,
a b c
得 x=2;用海伦公式求面积得 p= =9,S ABC 9(9 6)(9 5)(9 7) 6 6 ,而2
S 2 6 ABC S AOB S BOC S AOC 9 OD=6 6 ,OD= ;由等面积法知BD OD BO DH3
4 7 8 7
得 DH= ,故 DE=
7 7
9 2
13.解:连接 BD、OD、BF,易知S BOD S BOC ,故 OB||DF,故S BOF ,而S BOE 3 2 ,2
S 3 2 6 2故 BEF ,S BOD SBEGD 过点 D作 GH||BE,易知 BDH ~ DFG设 B(m, ),2 m
n, 6 2 S 1 (6 2 6 2 )(n m) 9 2 , n 2m m : 3 2 3 3D( ),故 BEGD ,而 : 2mn 2 m n 2 m m
3 3
得 m= 3 ,故 F( ,0)
2
AH EH 3
14.作 AH BC于点 H,连接 DH、EH,由已知得 得△BDH~△AEH,∠CDE=
BH DH 4
CD 4
∠DAF得∠CDH=∠BFA,∠C=∠ABF,故△CDH~△BFA,
BF 5
15.解:过点 B、C分别为 AD的垂线于点 H、M,设∠ACD=α,则∠ABD=2α,得∠BDC=∠
BCD=60°-α,故 A、C、D在以 B为圆心,BA为半径的圆上;设 AH=2 3 k,则 BH=5k,得
k=1,设 CM=x,则 DM= 3x,AM= 3x 11 4 3,故 x= ,故 CD=11
2
16.解:延长 BD交 CF延长线于点 G,易知△ABD≌△CGD,BC=6,可得 AC=12,CD=6,
1 1
故∠CDB=45°,而 tan∠A= ,故 tan∠ABD= ,同时 BD=DG,∠FBD=∠G=∠ABD,故 tan∠
2 3
1
FBD= ,故 DF=2 2
3
17.作 CD⊥BC、AE⊥AB交于点 E,连接 DE,AB=CD,,AB=CE得 CD=CE,∠BCD=30°,
得∠DCE=60°,故△CDE为等边三角形,DE=CE=AE,得 AE=2AD,∠AED=30°,故
∠ADE=90°,故∠BAD=30°
18.解:延长 BE交 CD于点 G,作 DH⊥EG于点 H,易知△ABE≌△DGA,BE=GE,BC=CG,
EF AE 1 2 3
故 CE⊥BG,设 AB=2,则 DG=2,AC=2 3,DH=1,GH= 3;而 ,EF
BF BC 2 3
5 3 3
故,HF= ,故 tan∠DFE=
3 5
2
19.解:连接 AC,作 AH⊥CF于点 H,AH= AG,而 AC= 2 BC,而 AG=BC,故 AC=2AM,
2
故∠ACM=30°,作 FI⊥AG于点 I,易知 FI=GI=1,AI= 3,AF=2,故 BF= 3 -1,故 CF=2 2
20.解:作 BE⊥AD于点 E,得 AE=BE=4,得 DE=3,连接 BD得 BD=5,故△BCD为等腰
直角三角形,作 CF⊥AD于点 F,易得△CDF≌△DBE,得 DF=4,CF=3,故 AC= 130
21.解:作 AH⊥BM交 CE于点 H,设∠ACD=2α,则∠ABM=∠AMB=α,∠DAH=α,易知
△ABN≌△DAH,∠HAE=∠AHE=90°-α,故 EA=EH,设 AM=x,则 AD=x,DE=x+1,由勾
股定理得(x+1)2+x2=(x+3)2得 x=3+ 17 ,DN=1+ 17
22.解:思路 1:一线三角得全等
如图 1在 y轴上取 D、E两点,使∠BDA=60°,∠CEA=60°,作 CF AE于点 F,易知
m 2m m
ABD CAE,AE=BD,AD=CE,EF= ,CE= ,故 AE=1+ ,由 BD=2OD得
3 3 3
1 m 2( 2m 2) 5 3 ,得 m=
3 3 3
思路 2:一线三角得相似
第一个图,作 AD AB交 BC延长线于点 D,作 DE y轴,易知 ADE~ BAO,相似比
为 AD:AB= 3,设 OB=n,则 AE= 3 a,DE=2 3,故 D(2, 3 a),而 C为 BD的中点,
n 2 3 m, 2 3n 0 5 3故 3 ,得 m=
2 2 3
思路 3:构手拉手全等
以 AO为边作等边三角形 AOD,连接 CD,由 AO=AD,AB=AC,∠OAB=∠CAD,得
AOB ADC,故∠ADC=∠AOB=90°,易知 D( 3,1),AD2+CD2=AC2,
22+(m- 3 )2+22 5 3=m2+32,得 m=
3
思考 4:共圆
①在 x轴上取点 D,使 ADO=60,易知 A、D、B、C共圆,连接 DC,得 CDB=60,故 CD
的解析式为 y 3(x 2 5 3 ),将 C(m,3)代入得 m=
3 3
②作 CD y轴于点 D,CE AB于点 E,连接 DE,易知 A、D、C、E共圆,易知∠CDE=60°,
故∠EDA=30°,作 EF y轴于点 F,E为 AB的中点,故 F为 OA的中点,故 AF=1,故 DF=2,
2 3 21 2 21 5 3 5 3
EF= ,得 AE= ,故 AC= ,故 CD= ,故 m=
3 3 3 3 3
23.解:连接 EC,作 DH EC 于点 H,设∠EDC=2α,则 F=α,而 DE=DC=5,故∠DCE=∠
DEC=90°-α,故∠BCE=α,故 EC||AF,故 CF=6
24.解:作 FH PC于点 H,由 AB=5 得 AC=5 2 ,AE= 2 ,CE=4 2 ,由∠FEG=∠FCG=90°
EC EF 13 2
知点 G、F、C、E共圆,得∠EFG=45°,△ECF~△EFP, 得 PE=
EF PE 2
25.解:由 AB=AC,OB=OC,OA=OA,△AOB △AOC,∠BAD=∠AOD=2∠OAD,故
OA OD
△AOD~△BAD, , AD2 OD BD设 OD=x,则有 AD= x(x 1) ,
BA AO
x(x 1) 2 x(x 1) x(x 1)AB= ,而AD AB DC故 x(x 1) ( x(x 1)) 得
x x x
5 1
x=
2
26.解:连接MA、MC、BM,在 CD上取一点 E,使 EC=AB,M为弧的中点,故 AM=CM,
∠BAM=∠MCE,故△ABM △CEM,MB=ME,ME BE,故 CD=3 2
2 3 4 3 3
27.解:连接 AD、OC、OF,CD=2,DO= ,OC= ,OH= ,DH=1,得 EF= 5,
3 3 3
故 DE= 5 -1
28.解:连接 PB、FA、FB,易知 E为 AB和 PF的中点,故 PBFA为平行四边形,易知
FB FD
△FBD~△FPB,得 ,FB2 FD PF ,PA= 6
PF FB
29.解:引△ABC的外接圆,延长 CP交圆于点 D,易知∠BAC=∠ACD=48°,故 BC=AD,
而 BC=PA,故 PA=AD,故∠ADC=∠APD=76°,故∠DAP=28°,故∠DAB=8°,故∠BCP=8°
30.解:引△ABC的外接圆,连接 OA,作 OD BC,连接 IC,DG AC,∠ICD=∠ICB+∠
BCD,∠CID=∠CAD+∠ACI,故∠CID=∠ICD,CD=DI,而 DI=AI得 CD=AI,易得
1 1
△CDE △AIG,AG=CE= BC;同时 AG= (AB AC BC),代入数据可得 AC=8.
2 2
1.如图,a||b||c,直线 a与直线 b之间的距离为,直线 c与直线 b之间的距离为,等边 ABC
的三个顶点分别在直线 a、b、c上,则等边 ABC的边长为________
2.如图,正方形 ABCD中,E为 BC中点,连接 AE,DF⊥AE于点 F,连接 CF,FG⊥CF
AF 2
交 AD于点 G,下列结论:①CF=CD;②G为 AD中点;③△DCF∽△AGF;④ ,
EF 3
其中结论正确的是__________
3.如图,在矩形 ABCD中,AB= 3,AD=3;连接 BD,O是 BD中点,点 G由 A出发以
每秒一个单位向 D运动,连接 OG,直线 OG交 BC于 F,过 A作 AE⊥GF于 E,连接
DE,设运动时间为 t(0<t<3),则以下结论正确的是____________.
①当且仅当 t=1时,△DFG为等边三角形;②当且仅当 t=1 时,△AEG和△BCD相
3 3 21 3
似;③当 t= 时,CF= 2 AE;④在运动的过程中,DE有最小值为 .
2 4
4.如图,在 Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,P是 AE边上一点,
PC 3 CK
连结 PC并延长交 HI于点 Q,连结 CG交 AB于点 K.若 ,则
CQ 4 KG _________
5.如图,任意画一个∠A=60°的△ABC,再分别作△ABC的两条角平分线 BE和 CD,BE
和 CD相交于点 P,连接 AP,有以下结论:①∠BPC=120°;②AP平分∠BAC;③
点 P到边 AB,AC,BC的距离相等;④BD+CE=BC;⑤ AD AE 3AP,其中正
确的是_________
6.如图,Rt△ABC中,∠ACB=90°,AC=BC,D、E分别在 AC、BC上,CE=AD,CG
⊥DE于点 F,FE=1,FG=3,则 AC= .
7.如图,在△ABC中,AB=AC,点 D在 BC的延长线上,连接 AD,若∠B+3∠D=180°,
BC=2CD=4 ,则 AB= .
8.如图,正方形 ABCD中,E是 BC的中点,F在 CD上,CF=2DF,连接 AE、AF与对
角线 BD交于点M、N,连接MF、EN,给出结论:①∠EAF=45°;②AN EN;③tan
∠AMN=3;④DN:MN:BM= 2 : 5 : 3 ,其中正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
9.如图,点 D为 Rt ABC斜边 AB的中点,过点 D作 DE CD交 BC于点 E,若 BE=2,
AC=5,则 CE=________
10.如图,在 ABCD中,对角线 AC、BD交于点 O,AF平分∠BAC,交 BD于点 E,
交 BC于点 F,若 BE=BF=2,则 AD=___________
11.如图,在 Rt△ABC中,AB=AC,点 D、E是线段 AC上两动点,且 AD=CE,AM垂
直于 BD,垂足为M,AM的延长线交 BC于点 N,直线 BD与直线 NE相交于点 F,当
EF
∠ABD=30°时, =______
BC
12.如图,△ABC的内切圆⊙O与 AB,BC,AC相切于点 D,E,F,已知 AB=6,AC
=5,BC=7,则 DE的长是( )
13.如图,四边形OABC 为矩形,点 A在第二象限,点 A关于OB的对称点为点D,点 B,
D 6 2都在函数 y (x 0)的图象上,BE x轴于点 E.若DC的延长线交 x轴于点 F ,当
x
矩形OABC 9 2 EF的面积为 时, 的值为 ,点 F 的坐标为 .
OE
3
14.如图,△ABC中,AB=AC,tanC= ,D、F分别在边 AC、BC上,作 AE⊥BD,DE
4
AE 3 CD
∥AF交 AE于 E.若 ,则 = .
BD 4 BF
15.如图,△ABC为等边三角形,点 D在△ABC外,连接 BD、CD.若∠ABD=2∠ACD,
2 3
tan∠ACD= ,BD= 37 ,则 CD= .
5
1
16.如图,Rt△ABC,∠C=90°,tanA= ,D是 AC中点,∠ABD=∠FBD,BC=6,
2
CF∥AB,则 DF= .
17.如图,已知 AB=CD,BC=2AD,∠ABC=90°,∠BCD=30°,则∠BAD=______
18.点 E是平行四边形 ABCD的边 AD的中点,AB AC,BE CE,则 tan∠DFE=_____
19.如图,点E、F在正方形ABCD边上,AE与CF交于点G,若AG=BC= 3 1,∠CGE=45°,
则 CF=____
20.如图,四边形 ABCD中,∠BAD=∠BCD=45°,AB=4 2 ,CD=5,AD=7,则 AC=_______
1
21.如图所示,ABCD为正方形,ADEF为矩形,∠AMB= ∠AED,若 AN=2,ME=3,则
2
DN=______
22.已知点 A(0,2),点 B在 x轴正半轴上,将 AB绕点 A逆时针旋转 60°至 AC,点 C(m,3),则
m=____
23.如图,矩形 ABCD中,AB=5,BC=4,点 E是 AB边上一点,AE=3,连接 DE,点 F是
1
BC延长线上一点,连接 AF,且∠F= ∠EDC,则 CF=_______
2
24.如图,正方形 ABCD的对角线 AC上有一点 E,且 CE=4AE,点 F在 DC的延长线上,
连接 EF,过点 E作 EG EF,交 CB的延长线于点 G,连接 GF并延长,交 AC延长线于点
P,若 AB=5,CF=2,则线段 EP的长是________
25.如图,已知⊙O的半径为 1,AB、AC是⊙O的两条弦,且 AB=AC,延长 BO交 AC于
点 D,若 AD2=AB DC,则 OD=______
26.如图,AB和 BC是⊙O的两条弦(即 ABC是圆的一条折弦),BC>AB,M是弧 ABC的中
点,则从M向 BC所作垂线的垂足 D是折弦 ABC的中点,若 AB=2 2 ,BD= 2 ,则
CD=_______
27.如图, ABC是圆 O的内接三角形,弦 EF过 BC的中点 D,且 EF||AB,若 AB=4,则
DE的长为__________
28.如图, ABC内接于圆 O,过 BC的中点 D作直线 l||AC,l与 AB交于点 E,与圆 O交
于点 G、F,与圆 O在点 A处的切线交于点 P,若 PE=3,DE=2,EF=3,则 PA的长为_________
29.已知 P为 ABC内一点,满足∠BAP=20°,∠CAP=28°,∠ACP=48°,AP=BC,则
∠BCP=______
30.如图,在 ABC中,AB=12,BC=10, ABC的内心、外心分别为点 I、O,且有 OI⊥
AI,则 AC=______
中考数学真题经典(十)参考答案
1.解:如图所示,在直线 c上取点 D、E,使∠BDC=∠AEC=60°,易知△BCD △CAE,
AE=CD作 BG⊥c,AH⊥c于 G、H,BG=2 3,AH=3 3,DG=2,BD=4,故 CG=4,HE=3,
AE=6,得 BC=2 7
2. 解:延长 AE交 DC延长线于点 H,易知△ABE △HCE,CH=AB,故 C为 DH的中点,
故 CF=CD,正确;由 CF=CD得∠CFD=∠CDF,故∠GFD=∠GDF,DF=GD而∠DAF+∠
ADF=∠AFG+∠DFG=90,得∠GAF=∠GFA,故 AG=GF,故 AG=DG,G为 AD的中点;
由∠GAF=∠CDF,故△DCF~△AGF;tan∠DAF=2,得 DF=2AF,FH=2DF,故 FH=4AF,
AF:EF=2:3;故①①③正确.
3. 解:当 t=1时,∠CDF=30°,∠FDG=60°,DF=2,而 AG=CF=1,故 DG=2,△DFG
为等边三角形;t=2 时,△AEG与△BCD相似,故错误;AG=CF,当 CF= 2 AE时有∠
3 3 3
AGE=45°,OH=GH= ,故 t=AG= ;点∠AEO=90°,点 E在以 AO为直径的圆
2 2
21 3
上运动,当 H、E、D共线时,DE取最小值,最小值为 ,故①正确.
2
4.解:作 CM⊥AB于点M,易知△ACP~△ICQ得 AC:CI=3:4,设 AC=3,则 BC=4,AB=5,
12
得 CM= ,CM||BG,CM:KG=CM:BG=12:25
5
5.解:由角平分线的性质可知∠BPC=90°+∠BAC,而∠BAC=60°,故∠BPC=120°,①正确;
三角形内角平分线交于一点,故 PA平分∠BAC,②③正确;在 BC上截取一点 F使 BF=BD,
易知△BPD △BPF和△CPF △CPE,④正确;作 PM⊥AB,PN⊥AC,易得
△PDM △PEN,AD+AE=2AM=AP,故①②③④⑤正确.
6. 作 DH⊥AD交 AB于点 H,连接 CH、EH,得 AD=DH,而 AD=CE,故 DH=CE,故 CDHE
为矩形;同时∠ECF=∠CDE=∠ACH,∠CHG=∠A+∠ACH,∠CGH=∠B+∠BCG,故
∠CHG=∠CGH,故 CG=CH;设 CF=x,则 DE=x+3,DF=x+2,由射影定理知 CF2=EF DF得
x2=(x+2),x=2,故 CE= 5,CD=2 5,故 AC=3 5
7.解:在 AD上取一点M使MC=MD,设∠D=α,则∠AMC=∠ACM=2α,则 AM=AC,设
AB=3x,则MD=x,AD2-DH2=AC2-CH2,得 (4x)2 (4 7)2 (3x)2 (2 7)2,x=2 3 ,AB=6 3
1 1
8.解:由 tan∠DAF= ,tan∠BAE= ,得∠DAF+∠BAE=45°,故∠EAF=45°;
3 2
∠EAF=∠MBE=45°,故 A、B、E、M共圆,故∠AEN=∠ABN=45°,故 AN⊥NE;
∠AMN=∠AFD,故 tan∠AMN=3;易知△ADN~△ACE,设 AB=8,则 CE=4,DN=2 2 ;
△ABM~△ACF,CF=6,则 BM=3 2 ,故正确的为①②③,选 A.
9.延长 CD至点 F使 DF=CD,连接 BF,易证△ACD △BDF,∠DBF=∠A,得∠CBF=90°,
BF=AC=5,而 CD=DF,ED⊥CF故 EF=CE= 29
10.解:
方向一:等腰三角形
解:易知 ADE亦为等腰三角形,设∠OAE=ɑ,∠OAD=β,则∠BAF=ɑ,∠AEO=ɑ+β,故∠
x 2
x 2 OD AD
ABD=β,故 DAO~ DBA,设 AD=x,则 OD= ,而 ,故 2 x ,
2 AD BD x x 2
x=2+2 2
点评:由等腰三角形得到一系列角度关系,通过角度关系得到相似三角形.这个突破点属于
比较常规的,当不知如何解答时,推导角度关系明显不失为一种很好的方式.
另法:角平分线定理
由角度关系可得比较多的相似三角形,易知相似比为 2 .
AB AO
解: ABO~ ACB, 得AB2 2OA2 即有AB 2OA ,由角平分线定理知
AC AB
AB BF
,故 CF=2 2 ,AD=2+2 2
AC CF
(亦可由 ABE~ ACF AB AO BO 2求得 CF的长度)此结论 可作为后续解法的基
AC AB BC 2
本结论.
方向二:角平分线
由角平分线可以联想到角平分线的性质、对称图形、全等三角形,因为题目本身呈现出好几
个等腰三角形,更易往全等三角形的方向联想.通过辅助线,构造全等三角形解决线段长问
题.
解法 1:在 AB延长线上取一点 G,使 AG=AC,易知 AFG AFC,∠AGF=∠ACF,而
AB BE
∠ABE=∠ACB,故∠ABE=∠AGF,得 BE||GF, 得 GF=2 2 ,故 AD=2+2AG GF 2
解法 2:在 AC 上取一点 G,使 AG=AB,易知 ABF AGF,∠AFG=∠AFB,而
GF CF
∠AFB=∠BEF,故∠AEO=∠AFG BE||GF OB 2,得 , ,而 得 CF=2
OB BC 2BC 2
解法 3:延长 CA至点 G,使 AG=AB,易知 AF||BG AG BF 2, ,得 CF=2 2 ,故
AC CF 2
AD=2+2 2
4 BA H AH=AC AF||CH AB BF 2解法 :延长 至点 ,使 ,易知 , ,得 CF=2 2 ,故
AH CF 2
AD=2+2 2
方向三:由中点构造中位线、平行线
解法 5:过点 O 作 OH||BC AO OE 2, 得 OE= 2 ,而 OH=OE,故 CF=2 2 ,
AB BE 2
AD=2+2 2
6 C CG||OB AO OE 2解法 :过点 作 , 得 OE= 2 ,而 CH=CG,故 CF=2 2 ,
AB BE 2
AD=2+2 2
AB OB
解法 7:过点 O 作 OG||AB,易知 ABO~ OCG, ,CG= 2 +1,故OC CG
AD=BC=2+2 2
解法 8:过点 E作 EG||BC,易知 ABE AGE AG EG 2, ,EG= 2 ,CF=2 2 ,
AC CF 2
故 AD=2+2 2
解法 9:过点 C作 CG||AF,易知 AOE COG,易知 BCG为等腰三角形,EG=CF,而
OE=OG= 2 ,故 CF=2 2 ,AD=2+2 2
解法 10:作 BM AF,CN AF BM AB 2,易知 ABM~ ACN, ,而 BMF~ CNF,
CN AC 2
BF BM
,故 CF=2 2 ,AD=2+2CF CN 2
11. 解:过点 C作 CG AC交 AN延长线于点 G,AB=AC,∠ABD=∠CAG=30°,
∠BAD=∠ACG,故△ABD≌△CAG,CG=AD,而 AD=CE,故 CG=CE;CN=CN,NCE=NCG,
故△CNE≌△CNG;∠CEN=60°,故△EFD为等边三角形,设 NG=2a,则 GC=( 3 1)a,
AC=(3 3 EF 2 6 3 2)a,EF=( 3 1)a,BC=( 6 3 2 )a,故
BC 6
12.解:连接 OD、OE、OF,设 AF=x,则 AD=x,CE=CF=5-x,BE=BD=6-x,故 6-x+5-x=7,
a b c
得 x=2;用海伦公式求面积得 p= =9,S ABC 9(9 6)(9 5)(9 7) 6 6 ,而2
S 2 6 ABC S AOB S BOC S AOC 9 OD=6 6 ,OD= ;由等面积法知BD OD BO DH3
4 7 8 7
得 DH= ,故 DE=
7 7
9 2
13.解:连接 BD、OD、BF,易知S BOD S BOC ,故 OB||DF,故S BOF ,而S BOE 3 2 ,2
S 3 2 6 2故 BEF ,S BOD SBEGD 过点 D作 GH||BE,易知 BDH ~ DFG设 B(m, ),2 m
n, 6 2 S 1 (6 2 6 2 )(n m) 9 2 , n 2m m : 3 2 3 3D( ),故 BEGD ,而 : 2mn 2 m n 2 m m
3 3
得 m= 3 ,故 F( ,0)
2
AH EH 3
14.作 AH BC于点 H,连接 DH、EH,由已知得 得△BDH~△AEH,∠CDE=
BH DH 4
CD 4
∠DAF得∠CDH=∠BFA,∠C=∠ABF,故△CDH~△BFA,
BF 5
15.解:过点 B、C分别为 AD的垂线于点 H、M,设∠ACD=α,则∠ABD=2α,得∠BDC=∠
BCD=60°-α,故 A、C、D在以 B为圆心,BA为半径的圆上;设 AH=2 3 k,则 BH=5k,得
k=1,设 CM=x,则 DM= 3x,AM= 3x 11 4 3,故 x= ,故 CD=11
2
16.解:延长 BD交 CF延长线于点 G,易知△ABD≌△CGD,BC=6,可得 AC=12,CD=6,
1 1
故∠CDB=45°,而 tan∠A= ,故 tan∠ABD= ,同时 BD=DG,∠FBD=∠G=∠ABD,故 tan∠
2 3
1
FBD= ,故 DF=2 2
3
17.作 CD⊥BC、AE⊥AB交于点 E,连接 DE,AB=CD,,AB=CE得 CD=CE,∠BCD=30°,
得∠DCE=60°,故△CDE为等边三角形,DE=CE=AE,得 AE=2AD,∠AED=30°,故
∠ADE=90°,故∠BAD=30°
18.解:延长 BE交 CD于点 G,作 DH⊥EG于点 H,易知△ABE≌△DGA,BE=GE,BC=CG,
EF AE 1 2 3
故 CE⊥BG,设 AB=2,则 DG=2,AC=2 3,DH=1,GH= 3;而 ,EF
BF BC 2 3
5 3 3
故,HF= ,故 tan∠DFE=
3 5
2
19.解:连接 AC,作 AH⊥CF于点 H,AH= AG,而 AC= 2 BC,而 AG=BC,故 AC=2AM,
2
故∠ACM=30°,作 FI⊥AG于点 I,易知 FI=GI=1,AI= 3,AF=2,故 BF= 3 -1,故 CF=2 2
20.解:作 BE⊥AD于点 E,得 AE=BE=4,得 DE=3,连接 BD得 BD=5,故△BCD为等腰
直角三角形,作 CF⊥AD于点 F,易得△CDF≌△DBE,得 DF=4,CF=3,故 AC= 130
21.解:作 AH⊥BM交 CE于点 H,设∠ACD=2α,则∠ABM=∠AMB=α,∠DAH=α,易知
△ABN≌△DAH,∠HAE=∠AHE=90°-α,故 EA=EH,设 AM=x,则 AD=x,DE=x+1,由勾
股定理得(x+1)2+x2=(x+3)2得 x=3+ 17 ,DN=1+ 17
22.解:思路 1:一线三角得全等
如图 1在 y轴上取 D、E两点,使∠BDA=60°,∠CEA=60°,作 CF AE于点 F,易知
m 2m m
ABD CAE,AE=BD,AD=CE,EF= ,CE= ,故 AE=1+ ,由 BD=2OD得
3 3 3
1 m 2( 2m 2) 5 3 ,得 m=
3 3 3
思路 2:一线三角得相似
第一个图,作 AD AB交 BC延长线于点 D,作 DE y轴,易知 ADE~ BAO,相似比
为 AD:AB= 3,设 OB=n,则 AE= 3 a,DE=2 3,故 D(2, 3 a),而 C为 BD的中点,
n 2 3 m, 2 3n 0 5 3故 3 ,得 m=
2 2 3
思路 3:构手拉手全等
以 AO为边作等边三角形 AOD,连接 CD,由 AO=AD,AB=AC,∠OAB=∠CAD,得
AOB ADC,故∠ADC=∠AOB=90°,易知 D( 3,1),AD2+CD2=AC2,
22+(m- 3 )2+22 5 3=m2+32,得 m=
3
思考 4:共圆
①在 x轴上取点 D,使 ADO=60,易知 A、D、B、C共圆,连接 DC,得 CDB=60,故 CD
的解析式为 y 3(x 2 5 3 ),将 C(m,3)代入得 m=
3 3
②作 CD y轴于点 D,CE AB于点 E,连接 DE,易知 A、D、C、E共圆,易知∠CDE=60°,
故∠EDA=30°,作 EF y轴于点 F,E为 AB的中点,故 F为 OA的中点,故 AF=1,故 DF=2,
2 3 21 2 21 5 3 5 3
EF= ,得 AE= ,故 AC= ,故 CD= ,故 m=
3 3 3 3 3
23.解:连接 EC,作 DH EC 于点 H,设∠EDC=2α,则 F=α,而 DE=DC=5,故∠DCE=∠
DEC=90°-α,故∠BCE=α,故 EC||AF,故 CF=6
24.解:作 FH PC于点 H,由 AB=5 得 AC=5 2 ,AE= 2 ,CE=4 2 ,由∠FEG=∠FCG=90°
EC EF 13 2
知点 G、F、C、E共圆,得∠EFG=45°,△ECF~△EFP, 得 PE=
EF PE 2
25.解:由 AB=AC,OB=OC,OA=OA,△AOB △AOC,∠BAD=∠AOD=2∠OAD,故
OA OD
△AOD~△BAD, , AD2 OD BD设 OD=x,则有 AD= x(x 1) ,
BA AO
x(x 1) 2 x(x 1) x(x 1)AB= ,而AD AB DC故 x(x 1) ( x(x 1)) 得
x x x
5 1
x=
2
26.解:连接MA、MC、BM,在 CD上取一点 E,使 EC=AB,M为弧的中点,故 AM=CM,
∠BAM=∠MCE,故△ABM △CEM,MB=ME,ME BE,故 CD=3 2
2 3 4 3 3
27.解:连接 AD、OC、OF,CD=2,DO= ,OC= ,OH= ,DH=1,得 EF= 5,
3 3 3
故 DE= 5 -1
28.解:连接 PB、FA、FB,易知 E为 AB和 PF的中点,故 PBFA为平行四边形,易知
FB FD
△FBD~△FPB,得 ,FB2 FD PF ,PA= 6
PF FB
29.解:引△ABC的外接圆,延长 CP交圆于点 D,易知∠BAC=∠ACD=48°,故 BC=AD,
而 BC=PA,故 PA=AD,故∠ADC=∠APD=76°,故∠DAP=28°,故∠DAB=8°,故∠BCP=8°
30.解:引△ABC的外接圆,连接 OA,作 OD BC,连接 IC,DG AC,∠ICD=∠ICB+∠
BCD,∠CID=∠CAD+∠ACI,故∠CID=∠ICD,CD=DI,而 DI=AI得 CD=AI,易得
1 1
△CDE △AIG,AG=CE= BC;同时 AG= (AB AC BC),代入数据可得 AC=8.
2 2
同课章节目录
