苏教版初中数学七年级上册 第二章 有理数 复习课件(共46张PPT)
文档属性
| 名称 | 苏教版初中数学七年级上册 第二章 有理数 复习课件(共46张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 00:00:00 | ||
图片预览










文档简介
(共45张PPT)
有 理 数
第 一 讲
课程大纲
1、正数、负数和0
2、有理数的定义
3、有理数的分类
4、“六非问题”
正数、负数和0
+30℃
-20℃
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
正数:
负数:
大于0的数
小于0的数
0 ?
0既不是正数也不是负数
0为正数和负数的分界线
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
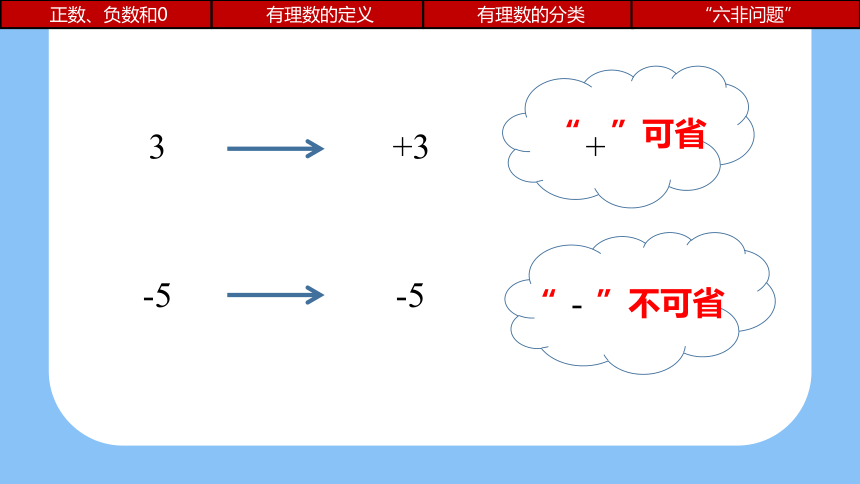
“ ”不可省
“ ”可省
3
+3
+
-5
-5
-
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
“ ”可省
负数
小于0的数
正数
大于0的数
0
既不是正数,也不是负数
数
“ ”不可省
-
+
记笔记
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
在 、 、-3、2、0、-4.5、1
中,负数有( )
A.1个 B.2个 C.3个 D.4个
1-1
例
C
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
如果 a 是一个数,那 -a
一定是一个( )
A. 正数
B. 负数
D. 0或正数或负数
C. 0
1-2
例
D
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
判断下列说法是否正确,正确的打“√” ,错误的打“×”
( ) 3、0是正数和负数的分界线
( ) 2、海拔高度是0米表示没有高度
( ) 1、不大于0的数一定是负数
( ) 4、不是正数的数一定是负数
( ) 5、a一定是负数
( ) 7、a为负数时,-a 一定是正数
( ) 6、不存在既不是正数也不是负数的数
( ) 8、没有最大的负数
√
√
√
×
×
×
×
×
1
练
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
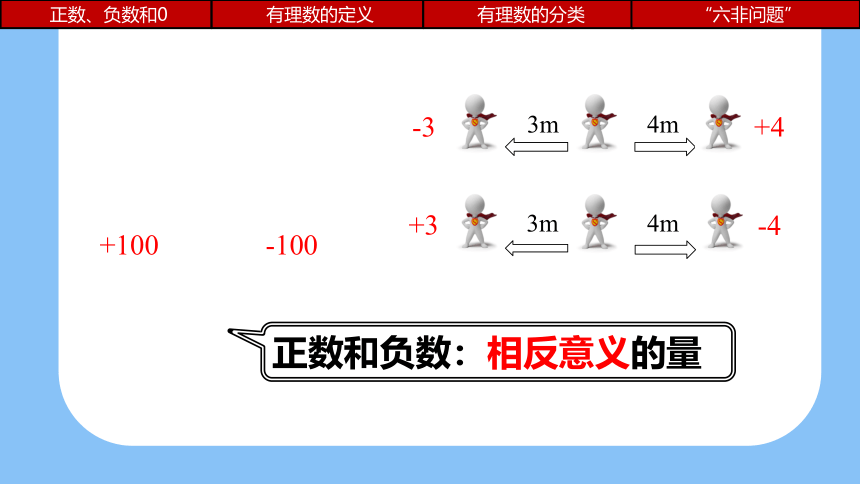
正数和负数:相反意义的量
4m
4m
3m
3m
+4
+3
-4
-3
-100
+100
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
(1)如果上升3米,记作+3米,那么下降5米,记作 米,不升不降记作 米
(2)在体育课跳远测试中,以4.00米为基准,若小东跳出了4.22米,可记作+0.22米,则小强跳出了3.95米,记作 .
(3)一运动员某次跳水过程中水面距离跳板3m,水面高度记作-3m,该运动员跳水的最高点离跳板2m,最高点可记作 m.
0
+2
2
例
-5
-0.05米
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
某商店出售三种不同品牌的大米,米袋上分别标有质量如下表:
大米的品牌 A B C
质量标示 (5±0.1)kg (5±0.3)kg (5±0.2)kg
现从中任意拿出两袋不同品牌的大米,这两袋大米
的质量最多相差( )
A.0.8kg B.0.6kg C.0.5kg D.0.4kg
C
2
练
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
纽约、悉尼与北京的时差如下表(正数表示同一时刻比北京时间快的时数,负数表示同一时刻比北京时间慢的时数):
当北京6 月15 日23 时,悉尼、纽约的时间分别是( )
A. 6 月16 日1 时;6 月15 日10 时
B. 6 月16 日1 时;6 月14 日10 时
C. 6 月15 日21 时;6 月15 日10 时
D. 6 月15 日21 时;6 月16 日12 时
城市 悉尼 纽约
时差/时 +2 -13
A
3
例
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
超市出售的三种品牌月饼袋上,分别标有质量为
(300±5)g,(300±10)g,(300±15)g,的字样,从中任意拿出两袋,它们的质量最多相差( )
10 g B. 20 g C. 30 g 40 g
C
3
练
A
B
C
D
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
一、数
负数
小于0的数 “-”不可省
正数
大于0的数 “+”可省
0
既不是正数也不是负数
总 结
记笔记
二、一个未知数a,有可能是正数、负数、0
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
有理数的定义
回 顾
整数按照符号可以分为:
正整数
负整数
0
0属于整数,0是区分正负的分界线
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
分数的形式为 遨游
分数按照符号可以分为
正分数
负分数
回 顾
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
思想遨游
小学我们学过哪些数?
小数的分类:
小数
有限小数
无限小数
无限循环小数
无限不循环小数
回 顾
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
定义:整数和分数统称为有理数。
有限小数、无限循环小数属于_______,
无限不循环小数则属于________。
有理数
无理数
记笔记
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
小试牛刀
5个
4个
3个
2个
2
例
B
0
0.1010010001...
2.3%
A
B
C
D
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
小试牛刀
(1)在 , , , , , , 有理数的个数有 ( )
3个
4个
5个
6个
2-1
练
D
0.1010010001
0
-4
3.14159
A
B
C
D
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
(2)在下列数 、 、 、 、 、 、
中,属于分数的有( )
2个 3个
4个 5个
2-2
练
B
-21
2.010010001...
3.1415926
25%
0
0.222...
A
B
C
D
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
有理数的分类
有理数的分类
有理数按定义分类
正整数
有理数
分数
整数
负整数
0
正分数
负分数
先定义
再正负
记笔记
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
、-2.25、
正分数 ( )
分数 ( )
、 、-2.25、0.3、 、10%
、0.3、10%
把下列各数分别填入相应集合内
3
例
整数 ( )
正整数 ( )
负整数 ( )
负分数 ( )
-10、6、 、0、 、-2.25、0.3、67、 、10%、-18、π
-10、6、0、67、-18
6、67
-10、-18
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
正整数
有理数
正分数
正有理数
0
负有理数
负整数
负分数
有理数按符号分类
有理数的分类
先正负
再定义
记笔记
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
把下列各数分别填入相应集合内
3
例
正有理数 ( )
负有理数 ( )
正整数 ( )
负整数 ( )
正分数 ( )
负分数 ( )
-10、6、 、0、 、-2.25、0.3、67、 、10%、-18、π
6、 、0.3、67、10%
-10、 、-2.25、 、-18
6、67
、0.3、10%
-10、-18
、-2.25、
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
判断下列说法是否正确,正确的打“√”,错误的打“×”
( ) 1、有理数是正数和负数的统称
( ) 2、正整数,负整数,正分数,负分数合在一起就是全体有理数
( ) 3、有理数是指整数,分数,正有理数,负有理数和0五类
( ) 4、有理数包括整数和分数
1
例
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
×
×
×
√
判断下列说法是否正确,正确的打“√”,错误的打“×”
( ) 1、一个有理数不是正数就是负数
( ) 2、零的意义是没有
( ) 3、零是最小的自然数
( ) 4、有理数不是整数就是分数
√
×
×
1
练
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
√
把下列各数的序号填在相应的集合内:
( 1 ) 100;
( 2 ) -99%;
( 4 ) 0;
( 5 ) -2008;
( 6 ) -2;
( 7 ) 5.2;
( 9 ) 6;
( 11 ) -0.3;
( 12 ) 1.020020002...
整数集
负数集
正数集
分数集
3-1
练
8
P
( 8 ) ;
( 9 )
( 3 ) π;
( 1 )
( 4 )
( 5 )
( 6 )
( 2 )
( 10 )
( 11 )
( 10 ) ;
( 1 )
( 3 )
( 9 )
( 12 )
( 7 )
( 8 )
( 2 )
( 10 )
( 11 )
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
“六非问题”
如果一个数不是正数,
那它是什么?
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
正数
负数
非正数
零
非负数
数
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
正整数
负整数
非正整数
零
非负整数
整数
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
正有理数
负有理数
非正有理数
零
非负有理数
有理数
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
知识点:“六非问题”
非负数
正数、0
非负有理数
正有理数、0
非负整数
正整数、0
非正数
0、负数
口诀:见非写0,
非正整数
0、负整数
非正有理数
0、负有理数
非后相反
记笔记
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
非正数:
非负数:
非正整数:
非负整数:
把下列个数分别填入相应的集合内:
}
{
}
{
}
{
}
{
3
例
-10、6、 、0、 、-2.25、0.3、67、 、10%、-18、π
6、0、 、0.3、67、10%、π
-10、 、0、-2.25、 、-18
-10、0、-18
6、0、67
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
整数 分数 正数 负整数 正分数 非负数 非负整数 无理数
0
-3.14
2
π
在下表适当的表格里打上“ ”号。
3-2
练
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
判断下列关于0说法是否正确,正确的打“√”,错误的打“×”
( ) 1、0是整数,但不是自然数
( ) 2、0既不是正数,也不是负数
( ) 3、0不是整数,是自然数
( ) 4、0没有实际意义
√
2
拓
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
×
×
×
正数、负数和0
有理数的定义
“六非问题”
1.有理数的概念:整数和分数统称为有理数
2.有理数按定义分类:
正整数
有理数
分数
整数
负整数
0
正分数
负分数
3.有理数按符号分类:
0
有理数
正分数
正有理数
负有理数
正整数
负整数
负分数
课堂总结
有理数的分类
4.“六非”:
口诀:见非写0,非后相反
非负数
正数、0
非负有理数
正有理数、0
非负整数
正整数、0
非正数
0、负数
非正整数
0、负整数
非正有理数
0、负有理数
课堂总结
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
下节课见!
有 理 数
第 一 讲
课程大纲
1、正数、负数和0
2、有理数的定义
3、有理数的分类
4、“六非问题”
正数、负数和0
+30℃
-20℃
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
正数:
负数:
大于0的数
小于0的数
0 ?
0既不是正数也不是负数
0为正数和负数的分界线
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
“ ”不可省
“ ”可省
3
+3
+
-5
-5
-
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
“ ”可省
负数
小于0的数
正数
大于0的数
0
既不是正数,也不是负数
数
“ ”不可省
-
+
记笔记
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
在 、 、-3、2、0、-4.5、1
中,负数有( )
A.1个 B.2个 C.3个 D.4个
1-1
例
C
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
如果 a 是一个数,那 -a
一定是一个( )
A. 正数
B. 负数
D. 0或正数或负数
C. 0
1-2
例
D
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
判断下列说法是否正确,正确的打“√” ,错误的打“×”
( ) 3、0是正数和负数的分界线
( ) 2、海拔高度是0米表示没有高度
( ) 1、不大于0的数一定是负数
( ) 4、不是正数的数一定是负数
( ) 5、a一定是负数
( ) 7、a为负数时,-a 一定是正数
( ) 6、不存在既不是正数也不是负数的数
( ) 8、没有最大的负数
√
√
√
×
×
×
×
×
1
练
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
正数和负数:相反意义的量
4m
4m
3m
3m
+4
+3
-4
-3
-100
+100
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
(1)如果上升3米,记作+3米,那么下降5米,记作 米,不升不降记作 米
(2)在体育课跳远测试中,以4.00米为基准,若小东跳出了4.22米,可记作+0.22米,则小强跳出了3.95米,记作 .
(3)一运动员某次跳水过程中水面距离跳板3m,水面高度记作-3m,该运动员跳水的最高点离跳板2m,最高点可记作 m.
0
+2
2
例
-5
-0.05米
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
某商店出售三种不同品牌的大米,米袋上分别标有质量如下表:
大米的品牌 A B C
质量标示 (5±0.1)kg (5±0.3)kg (5±0.2)kg
现从中任意拿出两袋不同品牌的大米,这两袋大米
的质量最多相差( )
A.0.8kg B.0.6kg C.0.5kg D.0.4kg
C
2
练
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
纽约、悉尼与北京的时差如下表(正数表示同一时刻比北京时间快的时数,负数表示同一时刻比北京时间慢的时数):
当北京6 月15 日23 时,悉尼、纽约的时间分别是( )
A. 6 月16 日1 时;6 月15 日10 时
B. 6 月16 日1 时;6 月14 日10 时
C. 6 月15 日21 时;6 月15 日10 时
D. 6 月15 日21 时;6 月16 日12 时
城市 悉尼 纽约
时差/时 +2 -13
A
3
例
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
超市出售的三种品牌月饼袋上,分别标有质量为
(300±5)g,(300±10)g,(300±15)g,的字样,从中任意拿出两袋,它们的质量最多相差( )
10 g B. 20 g C. 30 g 40 g
C
3
练
A
B
C
D
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
一、数
负数
小于0的数 “-”不可省
正数
大于0的数 “+”可省
0
既不是正数也不是负数
总 结
记笔记
二、一个未知数a,有可能是正数、负数、0
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
有理数的定义
回 顾
整数按照符号可以分为:
正整数
负整数
0
0属于整数,0是区分正负的分界线
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
分数的形式为 遨游
分数按照符号可以分为
正分数
负分数
回 顾
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
思想遨游
小学我们学过哪些数?
小数的分类:
小数
有限小数
无限小数
无限循环小数
无限不循环小数
回 顾
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
定义:整数和分数统称为有理数。
有限小数、无限循环小数属于_______,
无限不循环小数则属于________。
有理数
无理数
记笔记
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
小试牛刀
5个
4个
3个
2个
2
例
B
0
0.1010010001...
2.3%
A
B
C
D
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
小试牛刀
(1)在 , , , , , , 有理数的个数有 ( )
3个
4个
5个
6个
2-1
练
D
0.1010010001
0
-4
3.14159
A
B
C
D
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
(2)在下列数 、 、 、 、 、 、
中,属于分数的有( )
2个 3个
4个 5个
2-2
练
B
-21
2.010010001...
3.1415926
25%
0
0.222...
A
B
C
D
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
有理数的分类
有理数的分类
有理数按定义分类
正整数
有理数
分数
整数
负整数
0
正分数
负分数
先定义
再正负
记笔记
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
、-2.25、
正分数 ( )
分数 ( )
、 、-2.25、0.3、 、10%
、0.3、10%
把下列各数分别填入相应集合内
3
例
整数 ( )
正整数 ( )
负整数 ( )
负分数 ( )
-10、6、 、0、 、-2.25、0.3、67、 、10%、-18、π
-10、6、0、67、-18
6、67
-10、-18
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
正整数
有理数
正分数
正有理数
0
负有理数
负整数
负分数
有理数按符号分类
有理数的分类
先正负
再定义
记笔记
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
把下列各数分别填入相应集合内
3
例
正有理数 ( )
负有理数 ( )
正整数 ( )
负整数 ( )
正分数 ( )
负分数 ( )
-10、6、 、0、 、-2.25、0.3、67、 、10%、-18、π
6、 、0.3、67、10%
-10、 、-2.25、 、-18
6、67
、0.3、10%
-10、-18
、-2.25、
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
判断下列说法是否正确,正确的打“√”,错误的打“×”
( ) 1、有理数是正数和负数的统称
( ) 2、正整数,负整数,正分数,负分数合在一起就是全体有理数
( ) 3、有理数是指整数,分数,正有理数,负有理数和0五类
( ) 4、有理数包括整数和分数
1
例
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
×
×
×
√
判断下列说法是否正确,正确的打“√”,错误的打“×”
( ) 1、一个有理数不是正数就是负数
( ) 2、零的意义是没有
( ) 3、零是最小的自然数
( ) 4、有理数不是整数就是分数
√
×
×
1
练
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
√
把下列各数的序号填在相应的集合内:
( 1 ) 100;
( 2 ) -99%;
( 4 ) 0;
( 5 ) -2008;
( 6 ) -2;
( 7 ) 5.2;
( 9 ) 6;
( 11 ) -0.3;
( 12 ) 1.020020002...
整数集
负数集
正数集
分数集
3-1
练
8
P
( 8 ) ;
( 9 )
( 3 ) π;
( 1 )
( 4 )
( 5 )
( 6 )
( 2 )
( 10 )
( 11 )
( 10 ) ;
( 1 )
( 3 )
( 9 )
( 12 )
( 7 )
( 8 )
( 2 )
( 10 )
( 11 )
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
“六非问题”
如果一个数不是正数,
那它是什么?
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
正数
负数
非正数
零
非负数
数
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
正整数
负整数
非正整数
零
非负整数
整数
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
正有理数
负有理数
非正有理数
零
非负有理数
有理数
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
知识点:“六非问题”
非负数
正数、0
非负有理数
正有理数、0
非负整数
正整数、0
非正数
0、负数
口诀:见非写0,
非正整数
0、负整数
非正有理数
0、负有理数
非后相反
记笔记
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
非正数:
非负数:
非正整数:
非负整数:
把下列个数分别填入相应的集合内:
}
{
}
{
}
{
}
{
3
例
-10、6、 、0、 、-2.25、0.3、67、 、10%、-18、π
6、0、 、0.3、67、10%、π
-10、 、0、-2.25、 、-18
-10、0、-18
6、0、67
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
整数 分数 正数 负整数 正分数 非负数 非负整数 无理数
0
-3.14
2
π
在下表适当的表格里打上“ ”号。
3-2
练
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
判断下列关于0说法是否正确,正确的打“√”,错误的打“×”
( ) 1、0是整数,但不是自然数
( ) 2、0既不是正数,也不是负数
( ) 3、0不是整数,是自然数
( ) 4、0没有实际意义
√
2
拓
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
×
×
×
正数、负数和0
有理数的定义
“六非问题”
1.有理数的概念:整数和分数统称为有理数
2.有理数按定义分类:
正整数
有理数
分数
整数
负整数
0
正分数
负分数
3.有理数按符号分类:
0
有理数
正分数
正有理数
负有理数
正整数
负整数
负分数
课堂总结
有理数的分类
4.“六非”:
口诀:见非写0,非后相反
非负数
正数、0
非负有理数
正有理数、0
非负整数
正整数、0
非正数
0、负数
非正整数
0、负整数
非正有理数
0、负有理数
课堂总结
正数、负数和0
有理数的定义
有理数的分类
“六非问题”
下节课见!
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
