2022-2023学年沪教版(上海)数学九年级上册26.1二次函数的概念 课件(共15张PPT)
文档属性
| 名称 | 2022-2023学年沪教版(上海)数学九年级上册26.1二次函数的概念 课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 506.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 16:53:38 | ||
图片预览






文档简介
(共15张PPT)
26.1二次函数的概念
教学目标和要求:
使学生理解二次函数的概念,掌握根据实际问题列出二次函数关系式的方法,并了解如何根据实际问题确定自变量的取值范围。
复习旧知识,通过实际问题的引入,经历二次函数概念的探索过程,提高学生解决问题的能力.
通过观察、操作、交流归纳等数学活动加深对二次函数概念的理解,发展学生的数学思维,增强学好数学的愿望与信心,提高创新思维能力。
复习提问
一次函数的定义是什么?
【设计意图】复习这些问题是为了引入一元二次此函数做铺垫,帮助学生加深对函数定义的理解.
知识回顾
1.一元二次方程的一般形式是什么?
2。一次函数的定义是什么?
ax2+bx+c=0
形如y=kx+b(其中k ,b为常数且k≠0)的函数叫做x 的一次函数
(a≠0)
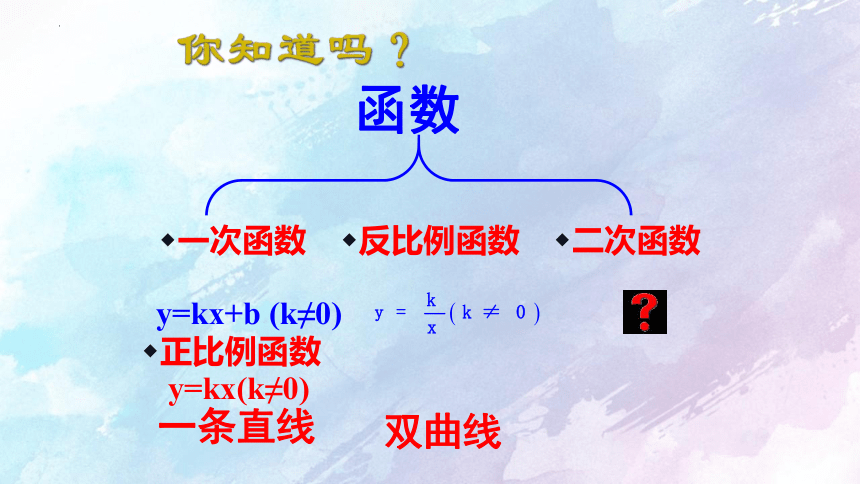
函数
一次函数
反比例函数
二次函数
正比例函数
y=kx+b (k≠0)
y=kx(k≠0)
一条直线
双曲线
例1. 下列关于x的函数,是不是二次函数?
是
不是
【概念辨析】
不是
是
不是
不是
不是
不是
归纳:( 化为最简式的前提下)
(1)二次函数解析式中,关于x的代数式一定是整式;
(2)整式中自变量的最高次数为二次.
是
【概念辨析】
例2.已知关于 x 的函数
若它是关于x的二次函数,求m的取值范围.
【概念辨析】
例2.已知关于 x 的函数
y=(m2-2m-3)x2+(m+1)x+m2.
(1)若它是关于x的二次函数,
m要满足的条件是 .
(2)若它是关于x的一次函数,
m要满足的条件是 .
一次函数 二次函数
解析式
y=ax +bx+c (a≠ 0)
y=kx+b (k≠ 0)
如图,用长为20米的篱笆,一面靠墙
(墙长度超过20米),围成一个矩形的花圃.设AB边的长为x米,花圃的面积为 y平方米.
(1)求y关于x的函数解析式及函数的定义域;
x
x
20-2x
B
C
D
A
(2)当x=6时,y的 值是多少?当y=32时,x的值多少?
(3)花圃的面积是否可能等于60平方米?为什么?
墙长度超过20米
(4)若题目的条件修改一下,那么第1.2问还一样吗?
探索问题1 正方体的六个面是全等的正方形,设正方形的棱长为x,表面积为y,显然对于x的每一个值,y都有一个对应值,即y是x的函数,它们的具体关系可以表示为?
设矩形靠墙的一边AB的长xm,矩形的面积ym2.能用含x的代数式来表示y吗?
教师提问:以上例子所列出的函数有什么特点,学生观察并讨论。
【设计意图】通过具体事例,让学生列出关系式,启发学生观察,思考,对比一次函数归纳出二次函数的定义
已知函数
(1) k为何值时,y是x的一次函数?
(2) k为何值时,y是x的二次函数?
解(1)根据题意得
∴k=1时,y是x的一次函数。
如果函数y=(k-3) +kx+1是二次函数,则k的值一定是______
0
如果函数y= +kx+1是二次函数,
则k的值一定是______
0,3
达标练习
2: m取何值时函数y= (m+2) xm2-2
+(m-3)x +m 是二次函数?
1、下列函数中是二次函数的是( )
A:y=3-2x2
C:y=(x-3) 2 -x2
D:y=x 3 -x2
A
B:y=x2 -
m=2
再见
26.1二次函数的概念
教学目标和要求:
使学生理解二次函数的概念,掌握根据实际问题列出二次函数关系式的方法,并了解如何根据实际问题确定自变量的取值范围。
复习旧知识,通过实际问题的引入,经历二次函数概念的探索过程,提高学生解决问题的能力.
通过观察、操作、交流归纳等数学活动加深对二次函数概念的理解,发展学生的数学思维,增强学好数学的愿望与信心,提高创新思维能力。
复习提问
一次函数的定义是什么?
【设计意图】复习这些问题是为了引入一元二次此函数做铺垫,帮助学生加深对函数定义的理解.
知识回顾
1.一元二次方程的一般形式是什么?
2。一次函数的定义是什么?
ax2+bx+c=0
形如y=kx+b(其中k ,b为常数且k≠0)的函数叫做x 的一次函数
(a≠0)
函数
一次函数
反比例函数
二次函数
正比例函数
y=kx+b (k≠0)
y=kx(k≠0)
一条直线
双曲线
例1. 下列关于x的函数,是不是二次函数?
是
不是
【概念辨析】
不是
是
不是
不是
不是
不是
归纳:( 化为最简式的前提下)
(1)二次函数解析式中,关于x的代数式一定是整式;
(2)整式中自变量的最高次数为二次.
是
【概念辨析】
例2.已知关于 x 的函数
若它是关于x的二次函数,求m的取值范围.
【概念辨析】
例2.已知关于 x 的函数
y=(m2-2m-3)x2+(m+1)x+m2.
(1)若它是关于x的二次函数,
m要满足的条件是 .
(2)若它是关于x的一次函数,
m要满足的条件是 .
一次函数 二次函数
解析式
y=ax +bx+c (a≠ 0)
y=kx+b (k≠ 0)
如图,用长为20米的篱笆,一面靠墙
(墙长度超过20米),围成一个矩形的花圃.设AB边的长为x米,花圃的面积为 y平方米.
(1)求y关于x的函数解析式及函数的定义域;
x
x
20-2x
B
C
D
A
(2)当x=6时,y的 值是多少?当y=32时,x的值多少?
(3)花圃的面积是否可能等于60平方米?为什么?
墙长度超过20米
(4)若题目的条件修改一下,那么第1.2问还一样吗?
探索问题1 正方体的六个面是全等的正方形,设正方形的棱长为x,表面积为y,显然对于x的每一个值,y都有一个对应值,即y是x的函数,它们的具体关系可以表示为?
设矩形靠墙的一边AB的长xm,矩形的面积ym2.能用含x的代数式来表示y吗?
教师提问:以上例子所列出的函数有什么特点,学生观察并讨论。
【设计意图】通过具体事例,让学生列出关系式,启发学生观察,思考,对比一次函数归纳出二次函数的定义
已知函数
(1) k为何值时,y是x的一次函数?
(2) k为何值时,y是x的二次函数?
解(1)根据题意得
∴k=1时,y是x的一次函数。
如果函数y=(k-3) +kx+1是二次函数,则k的值一定是______
0
如果函数y= +kx+1是二次函数,
则k的值一定是______
0,3
达标练习
2: m取何值时函数y= (m+2) xm2-2
+(m-3)x +m 是二次函数?
1、下列函数中是二次函数的是( )
A:y=3-2x2
C:y=(x-3) 2 -x2
D:y=x 3 -x2
A
B:y=x2 -
m=2
再见
