2022-2023学年数学沪教版(上海)九年级第一学期26.1二次函数的概念 课件(共17张PPT)
文档属性
| 名称 | 2022-2023学年数学沪教版(上海)九年级第一学期26.1二次函数的概念 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 161.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 17:04:48 | ||
图片预览





文档简介
(共17张PPT)
26.1二次函数的概念
教学目标 :
对二次函数概念的理解。
由实际问题确定函数解析式和确定自变量的取值范围。
喷泉的水线、桥拱、铅球和篮球的投球路线都不是直线,但它们的形态都相同。
我们称符合这种形态的曲线为抛物线,它就是我们本章将要学习的函数图象
复习与回顾
正比例函数
反比例函数
一次函数
函数
在某个变化过程中,有两个自变量,设为x和y,如果在变量x的允许取值范围内,变量y随着x的变化而变化,它们之间存在确定的依懒关系,那么变量y叫做变量x的函数
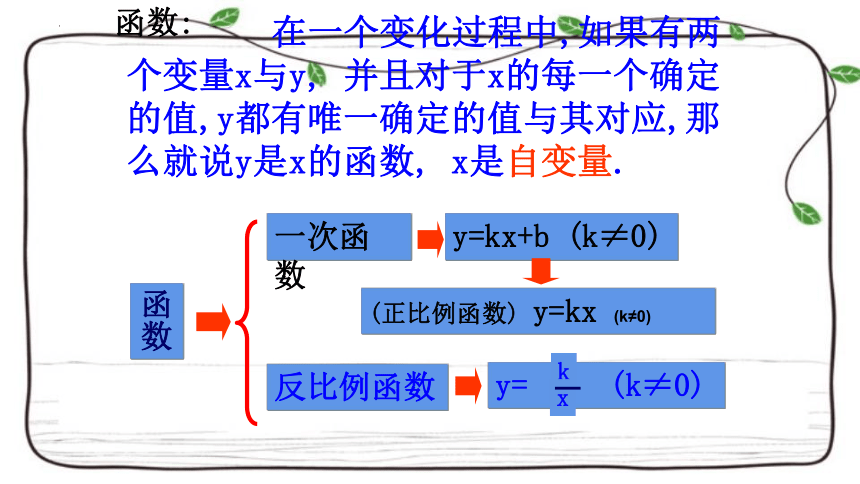
在一个变化过程中,如果有两个变量x与y, 并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么就说y是x的函数, x是自变量.
函数
一次函数
反比例函数
y=kx+b (k≠0)
(正比例函数) y=kx (k≠0)
y= (k≠0)
k
x
函数:
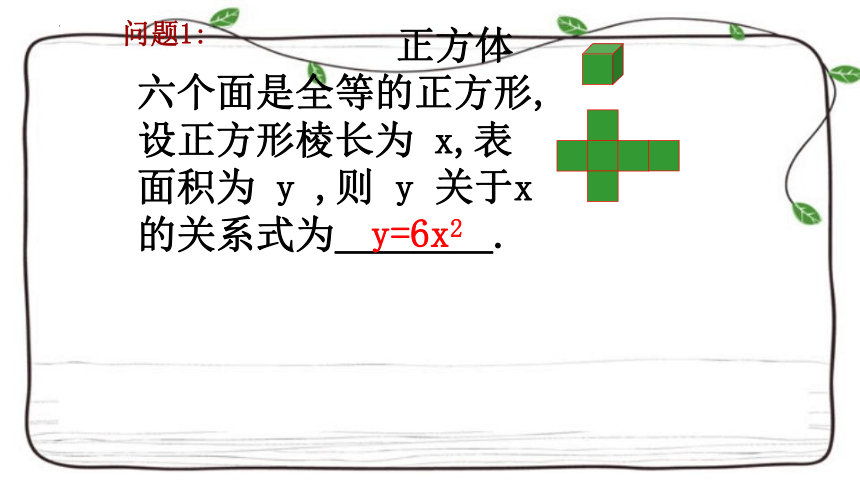
正方体六个面是全等的正方形,设正方形棱长为 x,表面积为 y ,则 y 关于x 的关系式为____.
问题1:
y=6x2
多边形的对角线数 d 与边数 n 有什么关系?
n边形有__个顶点,从一个顶点出发,连接与这点不相邻的各顶点,可作___条对角线.因此,n边形的对角线总数 d =______.
n
(n-3)
问题2:
n(n-3)
1
2
即:
通过研究函数可以帮助我们解决生活中的问题
分享曾经用函数解决的生活问题
1、如果正方形的边长是 x (cm),面积 y(cm2) 与边长 x 之间的函数关系是______________
2、一个边长为 4cm 的正方形,若它的边长增加 x cm,面积随之增加 y cm 2,
则 y =_________________________
y = x 2
( 4 + x ) 2 – 42
即 y = x 2 + 8x
新 课 引 入
3、把一根 40 cm 长的铁丝分成两段,再分别将每一段弯折成一个正方形,设其中一段铁丝为 x cm,两个正方形的面积和为y cm 2,
则y =_________________________
4、农机厂第一个月水泵的产量为50(台)第三个月的产量 y (台)与月平均增长率 x 之间的函数关系为 _________________________
y = 50( 1 + x ) 2
即 y = 50x 2 + 100x + 50
观察这些函数具有哪些共同的特征
y = x 2
y = x 2 + 8x
y = 50x 2 + 100x + 50
解析式都是用自变量的二次整式来表示,
我们称之为二次函数 ,
一般式为 y = ax 2 + bx + c
(其中:a、b、c 是常数,且a ≠ 0)
讲 解 新 课
问题1:
若圆的半径为x厘米,圆的面积为y平方厘米,试写出y关于x的函数解析式.
问题2:
甲、乙两数的和为20,设甲数为x,甲、乙两数的积为y,试写出y关于x的函数解析式.
问题3:
矩形的长为4厘米,宽为3厘米,将它的长与宽都增加x厘米,记现在矩形的面积为y平方厘米,试写出y关于x的函数解析式.
x
x
3
4
问题4:
汽车产业是我市支柱产业之一,产量和效益逐年增加. 据统计,2014年我市某种品牌汽车的年产量为6万辆,到2016年,该品牌汽车的年产量达到y万辆. 若该品牌汽车年产量的年增长率从2014年开始保持不变,均为x,试写出y关于x的函数解析式.
定义:
一般地,解析式形如
y=ax +bx+c (其中a、b、c是常数,且 a≠ 0)
的函数叫做二次函数.
二次函数y=ax +bx+c 的定义域为一切实数.
遇到实际问题,具体分析。
【思索归纳】
再见
26.1二次函数的概念
教学目标 :
对二次函数概念的理解。
由实际问题确定函数解析式和确定自变量的取值范围。
喷泉的水线、桥拱、铅球和篮球的投球路线都不是直线,但它们的形态都相同。
我们称符合这种形态的曲线为抛物线,它就是我们本章将要学习的函数图象
复习与回顾
正比例函数
反比例函数
一次函数
函数
在某个变化过程中,有两个自变量,设为x和y,如果在变量x的允许取值范围内,变量y随着x的变化而变化,它们之间存在确定的依懒关系,那么变量y叫做变量x的函数
在一个变化过程中,如果有两个变量x与y, 并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么就说y是x的函数, x是自变量.
函数
一次函数
反比例函数
y=kx+b (k≠0)
(正比例函数) y=kx (k≠0)
y= (k≠0)
k
x
函数:
正方体六个面是全等的正方形,设正方形棱长为 x,表面积为 y ,则 y 关于x 的关系式为____.
问题1:
y=6x2
多边形的对角线数 d 与边数 n 有什么关系?
n边形有__个顶点,从一个顶点出发,连接与这点不相邻的各顶点,可作___条对角线.因此,n边形的对角线总数 d =______.
n
(n-3)
问题2:
n(n-3)
1
2
即:
通过研究函数可以帮助我们解决生活中的问题
分享曾经用函数解决的生活问题
1、如果正方形的边长是 x (cm),面积 y(cm2) 与边长 x 之间的函数关系是______________
2、一个边长为 4cm 的正方形,若它的边长增加 x cm,面积随之增加 y cm 2,
则 y =_________________________
y = x 2
( 4 + x ) 2 – 42
即 y = x 2 + 8x
新 课 引 入
3、把一根 40 cm 长的铁丝分成两段,再分别将每一段弯折成一个正方形,设其中一段铁丝为 x cm,两个正方形的面积和为y cm 2,
则y =_________________________
4、农机厂第一个月水泵的产量为50(台)第三个月的产量 y (台)与月平均增长率 x 之间的函数关系为 _________________________
y = 50( 1 + x ) 2
即 y = 50x 2 + 100x + 50
观察这些函数具有哪些共同的特征
y = x 2
y = x 2 + 8x
y = 50x 2 + 100x + 50
解析式都是用自变量的二次整式来表示,
我们称之为二次函数 ,
一般式为 y = ax 2 + bx + c
(其中:a、b、c 是常数,且a ≠ 0)
讲 解 新 课
问题1:
若圆的半径为x厘米,圆的面积为y平方厘米,试写出y关于x的函数解析式.
问题2:
甲、乙两数的和为20,设甲数为x,甲、乙两数的积为y,试写出y关于x的函数解析式.
问题3:
矩形的长为4厘米,宽为3厘米,将它的长与宽都增加x厘米,记现在矩形的面积为y平方厘米,试写出y关于x的函数解析式.
x
x
3
4
问题4:
汽车产业是我市支柱产业之一,产量和效益逐年增加. 据统计,2014年我市某种品牌汽车的年产量为6万辆,到2016年,该品牌汽车的年产量达到y万辆. 若该品牌汽车年产量的年增长率从2014年开始保持不变,均为x,试写出y关于x的函数解析式.
定义:
一般地,解析式形如
y=ax +bx+c (其中a、b、c是常数,且 a≠ 0)
的函数叫做二次函数.
二次函数y=ax +bx+c 的定义域为一切实数.
遇到实际问题,具体分析。
【思索归纳】
再见
