北师大版九年级数学上册 4.2平行线分线段成比例同步测试题 (含解析)
文档属性
| 名称 | 北师大版九年级数学上册 4.2平行线分线段成比例同步测试题 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 404.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 00:00:00 | ||
图片预览



文档简介
2022-2023学年北师大版九年级数学上册《4.2平行线分线段成比例》同步测试题(附答案)
一.选择题(共8小题,满分32分)
1.如图,DE∥BC,且EC:BD=2:3,AD=6,则AE的长为( )
A.1 B.2 C.3 D.4
2.如图,已知AB∥CD∥EF,那么下列结论正确的是( )
A. B. C. D.
3.如图,a∥b∥c,若AC=5,AE=15,DF=12,则BD的长为( )
A.2 B.3 C.4 D.6
4.如图,直线l1∥l2∥l3,已知AE=1,BE=2,DE=3,则CD的长为( )
A. B. C.6 D.
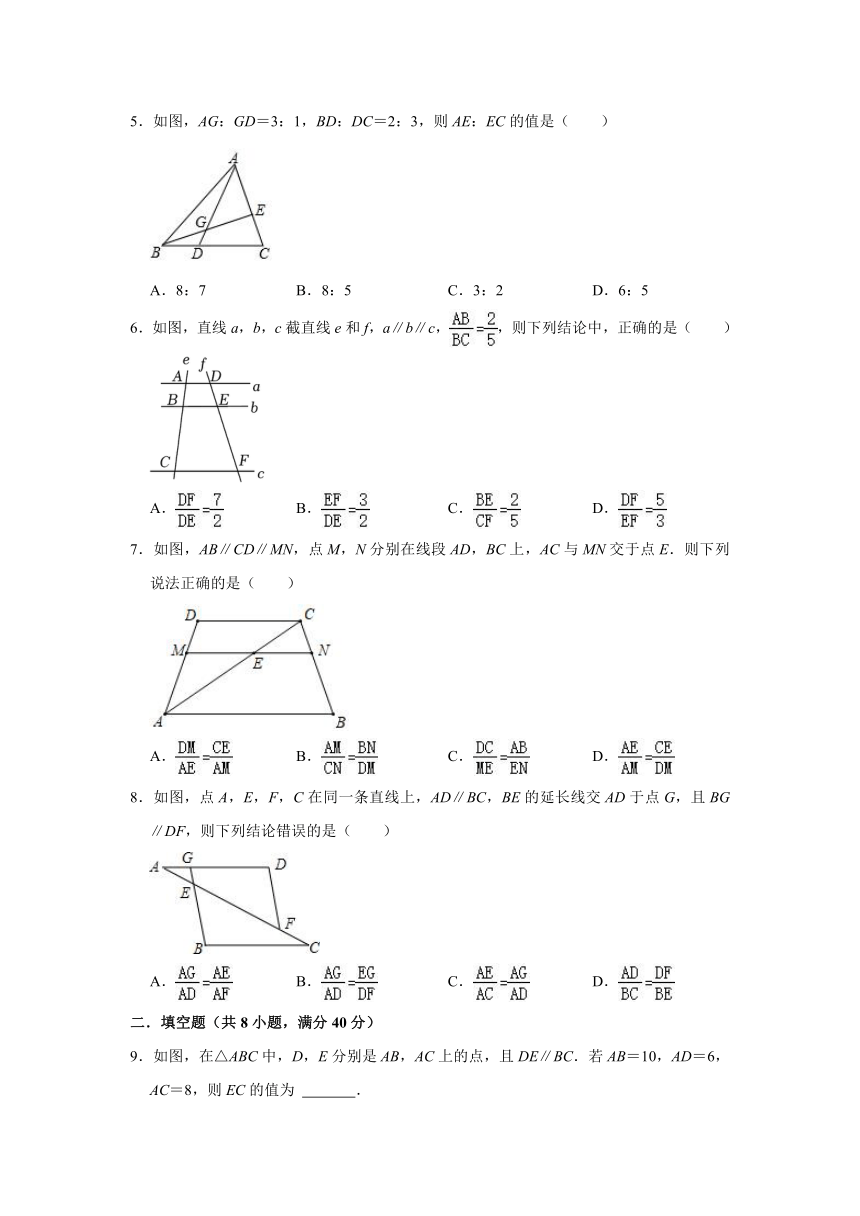
5.如图,AG:GD=3:1,BD:DC=2:3,则AE:EC的值是( )
A.8:7 B.8:5 C.3:2 D.6:5
6.如图,直线a,b,c截直线e和f,a∥b∥c,,则下列结论中,正确的是( )
A. B. C. D.
7.如图,AB∥CD∥MN,点M,N分别在线段AD,BC上,AC与MN交于点E.则下列说法正确的是( )
A. B. C. D.
8.如图,点A,E,F,C在同一条直线上,AD∥BC,BE的延长线交AD于点G,且BG∥DF,则下列结论错误的是( )
A. B. C. D.
二.填空题(共8小题,满分40分)
9.如图,在△ABC中,D,E分别是AB,AC上的点,且DE∥BC.若AB=10,AD=6,AC=8,则EC的值为 .
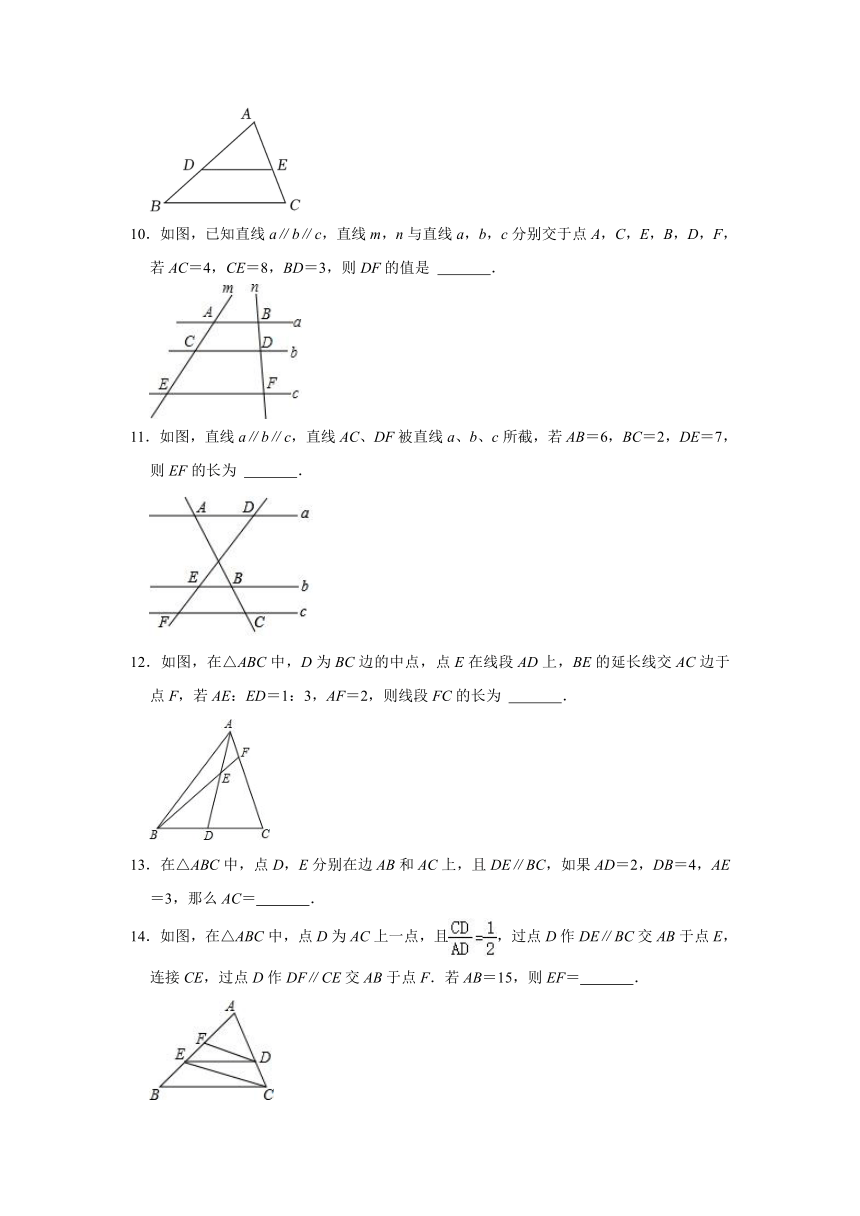
10.如图,已知直线a∥b∥c,直线m,n与直线a,b,c分别交于点A,C,E,B,D,F,若AC=4,CE=8,BD=3,则DF的值是 .
11.如图,直线a∥b∥c,直线AC、DF被直线a、b、c所截,若AB=6,BC=2,DE=7,则EF的长为 .
12.如图,在△ABC中,D为BC边的中点,点E在线段AD上,BE的延长线交AC边于点F,若AE:ED=1:3,AF=2,则线段FC的长为 .
13.在△ABC中,点D,E分别在边AB和AC上,且DE∥BC,如果AD=2,DB=4,AE=3,那么AC= .
14.如图,在△ABC中,点D为AC上一点,且,过点D作DE∥BC交AB于点E,连接CE,过点D作DF∥CE交AB于点F.若AB=15,则EF= .
15.如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=4,则GH的长为 .
16.如图,AB∥CD∥EF,点C,D分别在BE,AF上,如果BC=4,CE=6,AF=8,那么DF的长 .
三.解答题(共6小题,满分48分)
17.如图,在△ABC中,D、E、F分别是AB、BC上的点,且DE∥AC,AE∥DF,=,BF=6cm,求EF和FC的长.
18.如图,已知EG∥BC,GF∥CD,AE=3,EB=2,AF=6,求AD的长.
19.如图,l1∥l2∥l3,AB=3,AD=2,DE=4,EF=7.5.求BC、BE的长.
20.如图,在△ABC中,AM是BC边上的中线,直线DN∥AM,交AB于点D,交CA的延长线于点E,交BC于点N.求证:.
21.如图,AB∥CD∥EF,AC与BD相交于点E.
(1)填空:==;
(2)若CE=3,CF=2,AE=BC,求的值.
22.阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理,如图1,在△ABC中,AD平分∠BAC,则=.下面是这个定理的部分证明过程.
证明:如图2,过C作CE∥DA.交BA的延长线于E.…
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图3,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则△ABD的周长是 .
参考答案
一.选择题(共8小题,满分32分)
1.解:∵DE∥BC,
∴==,
即=,
解得:AE=4,
故选:D.
2.解:A.∵AB∥CD∥EF,
∴=≠,故本选项不符合题意;
B.∵AB∥CD∥EF,
∴=,故本选项不符合题意;
C.∵AB∥CD∥EF,
∴=,故本选项不符合题意;
D.∵AB∥CD∥EF,
∴=,故本选项符合题意;
故选:D.
3.解:∵a∥b∥c,
∴=,
∵AC=5,AE=15,
∴CE=10,
∵DF=12,
∴=
解得,BD=6,
故选:D.
4.解:∵l1∥l2∥l3,
∴=,
即=,
∴CE=,
∴CD=CE+DE=+3=.
故选:B.
5.解:过点D作DF∥BE交AC于点F,
则==,==3,
∴AE:EC=6:5,
故选:D.
6.解:∵a∥b∥c,,
∴=,
∴,,,故选项A正确,符合题意,选项B、D不正确,不符合题意;
连接AF,交BE于H,
∵BE∥CF,
∴△ABH∽△ACF,
∴,
,
∴选项C不正确,不符合题意;
故选:A.
7.解:A、∵AB∥CD∥MN,
∴=,本选项结论不正确;
B、∵AB∥CD∥MN,
∴=,本选项结论不正确;
C、∵AB∥CD∥MN,
∴=,=,
∴≠,本选项结论不正确;
D、∵AB∥CD∥MN,
∴=,本选项结论正确;
故选:D.
8.解:∵BG∥DF,∴=,A正确,C错误;
∴=,B 正确;
∵AD∥BC,∴∠A=∠C,
∵BG∥DF,∴∠BEC=∠DFA,
∴△BEC∽△DFA,
∴=,D正确,
故选:C.
二.填空题(共8小题,满分40分)
9.解:∵DE∥BC,
∴=,
∵AB=10,AD=6,AC=8,
∴=,
解得;AE=4.8,
∴EC=8﹣4.8=3.2,
故答案为:3.2.
10.解:∵直线a∥b∥c,
∴即,
∴DF=6.
故答案为6.
11.解:∵直线a∥b∥c,
∴=,
∵AB=6,BC=2,DE=7,
∴=,
∴EF=,
故答案为:.
12.解:如图,过点D作DG∥BF于点G;
则;
而,AF=2,
∴FG=6;
∵D为BC边的中点,
∴GF=GC=FC,
∴CF=2FG=12,
故答案为:12.
13.解:∵DE∥BC,
∴AD:AB=AE:AC,
∵AD=2,DB=4,AE=3,
∴2:6=3:AC,
∴AC=9,
故答案为:9.
14.解:∵DE∥BC,
∴=,
∵=,
∴=,即=,
∵AB=15,
∴AE=10,
∵DF∥CE,
∴=,即=,
解得:AF=,
则EF=AE﹣AF=10﹣=,
故答案为:
15.解:∵AB∥CH∥CD,
∴,,
∴+=+=1,
∵AB=2,CD=4,
∴+=1,
解得:GH=;
故答案为:.
16.解:∵AB∥CD∥EF,
∴,
∴=,
∴DF=,
故答案为:.
三.解答题(共6小题,满分48分)
17.解:∵AE∥DF,
∴=,即=,
∴EF=4,
∴BE=BF+EF=6+4=10,
∵DE∥AC,
∴=,即=,
∴CE=,
∴CF=CE+EF=.
18.解:∵AE=3,EB=2,
∴AB=5,
∵EG∥BC,GF∥DC,
∴,,
∴=,
∴=,
∴AD=10.
19.解:∵l1∥l2∥l3,
∴==,即==,
∴BC=6,BF=BE,
∴BE+BE=7.5,
∴BE=5.
20.证明:∵直线DN∥AM,
∴,,
∵在△ABC中,AM是BC边上的中线,
∴MB=MC,
∴.
21.解:(1)∵CD∥AB,
∴=,
∵EF∥AB,
∴=,
∴==;
故答案为BD,CF;
(2)∵=,
而CE=3,CF=2,AE=BC,
∴=,解得AE=6,
∴===.
22.(1)证明:如图2,过C作CE∥DA.交BA的延长线于E,
∵CE∥AD,
∴=,∠2=∠ACE,∠1=∠E,
∵∠1=∠2,
∴∠ACE=∠E,
∴AE=AC,
∴=;
(2)解:如图3,∵AB=3,BC=4,∠ABC=90°,
∴AC=5,
∵AD平分∠BAC,
∴=,即=,
∴BD=BC=,
∴AD===,
∴△ABD的周长=+3+=.
故答案为.
一.选择题(共8小题,满分32分)
1.如图,DE∥BC,且EC:BD=2:3,AD=6,则AE的长为( )
A.1 B.2 C.3 D.4
2.如图,已知AB∥CD∥EF,那么下列结论正确的是( )
A. B. C. D.
3.如图,a∥b∥c,若AC=5,AE=15,DF=12,则BD的长为( )
A.2 B.3 C.4 D.6
4.如图,直线l1∥l2∥l3,已知AE=1,BE=2,DE=3,则CD的长为( )
A. B. C.6 D.
5.如图,AG:GD=3:1,BD:DC=2:3,则AE:EC的值是( )
A.8:7 B.8:5 C.3:2 D.6:5
6.如图,直线a,b,c截直线e和f,a∥b∥c,,则下列结论中,正确的是( )
A. B. C. D.
7.如图,AB∥CD∥MN,点M,N分别在线段AD,BC上,AC与MN交于点E.则下列说法正确的是( )
A. B. C. D.
8.如图,点A,E,F,C在同一条直线上,AD∥BC,BE的延长线交AD于点G,且BG∥DF,则下列结论错误的是( )
A. B. C. D.
二.填空题(共8小题,满分40分)
9.如图,在△ABC中,D,E分别是AB,AC上的点,且DE∥BC.若AB=10,AD=6,AC=8,则EC的值为 .
10.如图,已知直线a∥b∥c,直线m,n与直线a,b,c分别交于点A,C,E,B,D,F,若AC=4,CE=8,BD=3,则DF的值是 .
11.如图,直线a∥b∥c,直线AC、DF被直线a、b、c所截,若AB=6,BC=2,DE=7,则EF的长为 .
12.如图,在△ABC中,D为BC边的中点,点E在线段AD上,BE的延长线交AC边于点F,若AE:ED=1:3,AF=2,则线段FC的长为 .
13.在△ABC中,点D,E分别在边AB和AC上,且DE∥BC,如果AD=2,DB=4,AE=3,那么AC= .
14.如图,在△ABC中,点D为AC上一点,且,过点D作DE∥BC交AB于点E,连接CE,过点D作DF∥CE交AB于点F.若AB=15,则EF= .
15.如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=4,则GH的长为 .
16.如图,AB∥CD∥EF,点C,D分别在BE,AF上,如果BC=4,CE=6,AF=8,那么DF的长 .
三.解答题(共6小题,满分48分)
17.如图,在△ABC中,D、E、F分别是AB、BC上的点,且DE∥AC,AE∥DF,=,BF=6cm,求EF和FC的长.
18.如图,已知EG∥BC,GF∥CD,AE=3,EB=2,AF=6,求AD的长.
19.如图,l1∥l2∥l3,AB=3,AD=2,DE=4,EF=7.5.求BC、BE的长.
20.如图,在△ABC中,AM是BC边上的中线,直线DN∥AM,交AB于点D,交CA的延长线于点E,交BC于点N.求证:.
21.如图,AB∥CD∥EF,AC与BD相交于点E.
(1)填空:==;
(2)若CE=3,CF=2,AE=BC,求的值.
22.阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理,如图1,在△ABC中,AD平分∠BAC,则=.下面是这个定理的部分证明过程.
证明:如图2,过C作CE∥DA.交BA的延长线于E.…
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图3,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则△ABD的周长是 .
参考答案
一.选择题(共8小题,满分32分)
1.解:∵DE∥BC,
∴==,
即=,
解得:AE=4,
故选:D.
2.解:A.∵AB∥CD∥EF,
∴=≠,故本选项不符合题意;
B.∵AB∥CD∥EF,
∴=,故本选项不符合题意;
C.∵AB∥CD∥EF,
∴=,故本选项不符合题意;
D.∵AB∥CD∥EF,
∴=,故本选项符合题意;
故选:D.
3.解:∵a∥b∥c,
∴=,
∵AC=5,AE=15,
∴CE=10,
∵DF=12,
∴=
解得,BD=6,
故选:D.
4.解:∵l1∥l2∥l3,
∴=,
即=,
∴CE=,
∴CD=CE+DE=+3=.
故选:B.
5.解:过点D作DF∥BE交AC于点F,
则==,==3,
∴AE:EC=6:5,
故选:D.
6.解:∵a∥b∥c,,
∴=,
∴,,,故选项A正确,符合题意,选项B、D不正确,不符合题意;
连接AF,交BE于H,
∵BE∥CF,
∴△ABH∽△ACF,
∴,
,
∴选项C不正确,不符合题意;
故选:A.
7.解:A、∵AB∥CD∥MN,
∴=,本选项结论不正确;
B、∵AB∥CD∥MN,
∴=,本选项结论不正确;
C、∵AB∥CD∥MN,
∴=,=,
∴≠,本选项结论不正确;
D、∵AB∥CD∥MN,
∴=,本选项结论正确;
故选:D.
8.解:∵BG∥DF,∴=,A正确,C错误;
∴=,B 正确;
∵AD∥BC,∴∠A=∠C,
∵BG∥DF,∴∠BEC=∠DFA,
∴△BEC∽△DFA,
∴=,D正确,
故选:C.
二.填空题(共8小题,满分40分)
9.解:∵DE∥BC,
∴=,
∵AB=10,AD=6,AC=8,
∴=,
解得;AE=4.8,
∴EC=8﹣4.8=3.2,
故答案为:3.2.
10.解:∵直线a∥b∥c,
∴即,
∴DF=6.
故答案为6.
11.解:∵直线a∥b∥c,
∴=,
∵AB=6,BC=2,DE=7,
∴=,
∴EF=,
故答案为:.
12.解:如图,过点D作DG∥BF于点G;
则;
而,AF=2,
∴FG=6;
∵D为BC边的中点,
∴GF=GC=FC,
∴CF=2FG=12,
故答案为:12.
13.解:∵DE∥BC,
∴AD:AB=AE:AC,
∵AD=2,DB=4,AE=3,
∴2:6=3:AC,
∴AC=9,
故答案为:9.
14.解:∵DE∥BC,
∴=,
∵=,
∴=,即=,
∵AB=15,
∴AE=10,
∵DF∥CE,
∴=,即=,
解得:AF=,
则EF=AE﹣AF=10﹣=,
故答案为:
15.解:∵AB∥CH∥CD,
∴,,
∴+=+=1,
∵AB=2,CD=4,
∴+=1,
解得:GH=;
故答案为:.
16.解:∵AB∥CD∥EF,
∴,
∴=,
∴DF=,
故答案为:.
三.解答题(共6小题,满分48分)
17.解:∵AE∥DF,
∴=,即=,
∴EF=4,
∴BE=BF+EF=6+4=10,
∵DE∥AC,
∴=,即=,
∴CE=,
∴CF=CE+EF=.
18.解:∵AE=3,EB=2,
∴AB=5,
∵EG∥BC,GF∥DC,
∴,,
∴=,
∴=,
∴AD=10.
19.解:∵l1∥l2∥l3,
∴==,即==,
∴BC=6,BF=BE,
∴BE+BE=7.5,
∴BE=5.
20.证明:∵直线DN∥AM,
∴,,
∵在△ABC中,AM是BC边上的中线,
∴MB=MC,
∴.
21.解:(1)∵CD∥AB,
∴=,
∵EF∥AB,
∴=,
∴==;
故答案为BD,CF;
(2)∵=,
而CE=3,CF=2,AE=BC,
∴=,解得AE=6,
∴===.
22.(1)证明:如图2,过C作CE∥DA.交BA的延长线于E,
∵CE∥AD,
∴=,∠2=∠ACE,∠1=∠E,
∵∠1=∠2,
∴∠ACE=∠E,
∴AE=AC,
∴=;
(2)解:如图3,∵AB=3,BC=4,∠ABC=90°,
∴AC=5,
∵AD平分∠BAC,
∴=,即=,
∴BD=BC=,
∴AD===,
∴△ABD的周长=+3+=.
故答案为.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
