人教版八年级数学上册 11.2与三角形有关的角同步测试题 (含解析)
文档属性
| 名称 | 人教版八年级数学上册 11.2与三角形有关的角同步测试题 (含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 478.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 00:00:00 | ||
图片预览



文档简介
2022-2023学年人教版八年级数学上册《11.2与三角形有关的角》同步测试题(附答案)
一.选择题(共10小题,满分30分)
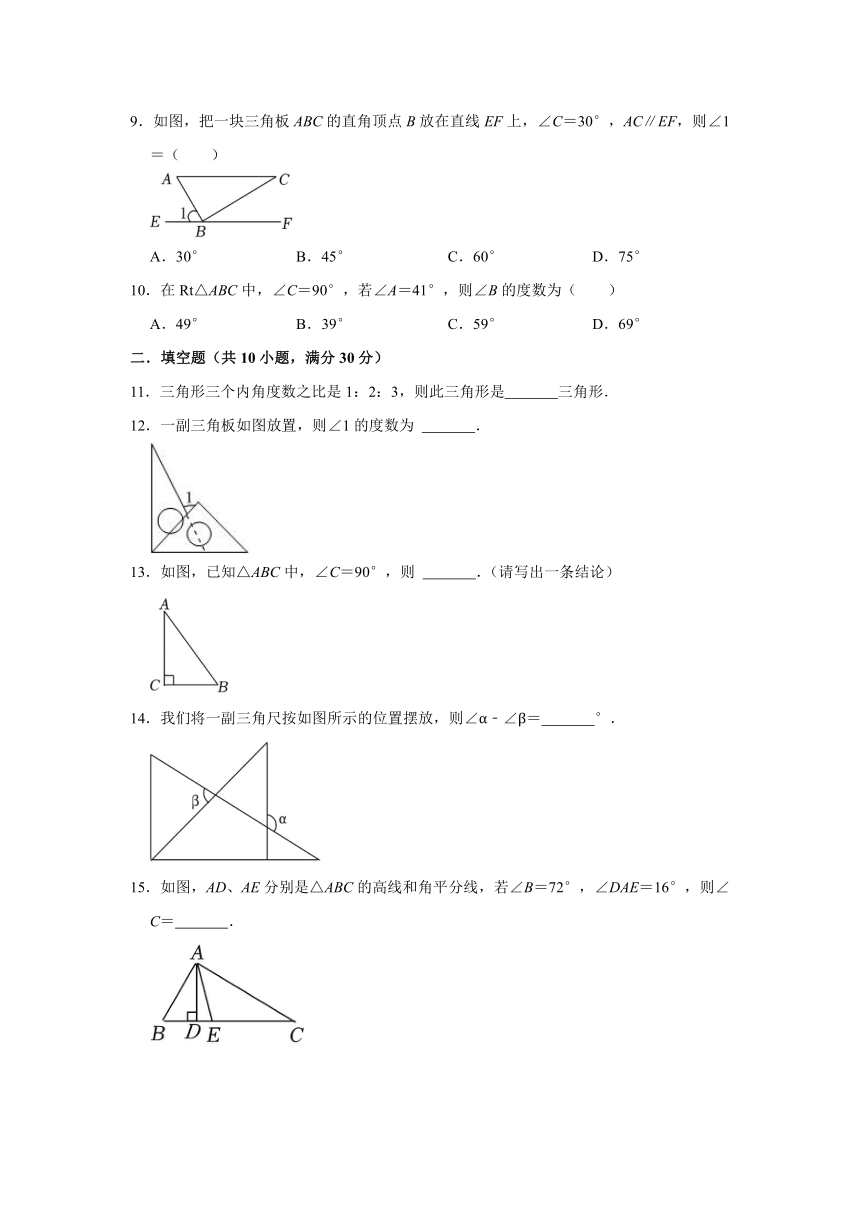
1.如图,在Rt△ABC中,∠A=90°,点B在直线EF上,点C在直线MN上,且直线EF∥MN,∠ACN=110°,则∠ABF的度数为( )
A.10° B.20° C.30° D.160°
2.如图,将一副直角三角板按如图所示的位置放置,则∠AOD的度数是( )
A.85° B.90° C.75° D.105°
3.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB,若∠BDE=56°,则∠DAE的度数为( )度.
A.23 B.28 C.52 D.56
4.如图所示,在四边形ABCD中,BD是它的一条对角线,若∠1=∠2,∠A=55°,则∠ADC=( )
A.110° B.115° C.125° D.135°
如图,△DEF是由△ABC经过平移得到的,已知∠B=110°,∠C=30°,则∠DGH的度数为( )
A.30° B.110° C.140° D.150°
6.如图,在△ABC中,BD和CE是△ABC的两条角平分线.若∠A=52°,则∠BOC的度数为( )
A.64° B.106° C.116° D.128°
7.如图,点D、E分别在线段BC、AC上,连接AD、BE.若∠A=35°,∠B=30°,∠C=45°,则∠AFB的大小为( )
A.75° B.80° C.100° D.110°
8.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,若∠ADC=65°,则∠BAC的大小为( )
A.35° B.50° C.65° D.70°
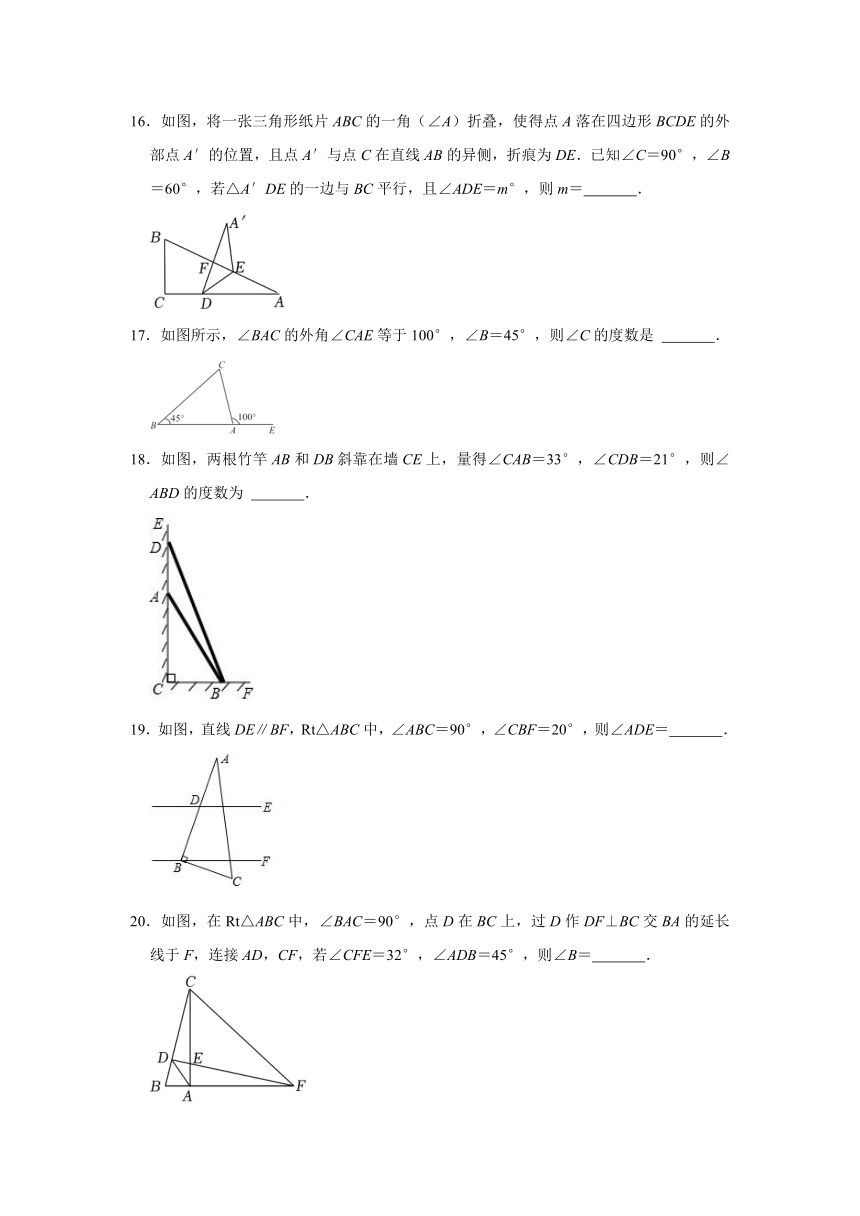
9.如图,把一块三角板ABC的直角顶点B放在直线EF上,∠C=30°,AC∥EF,则∠1=( )
A.30° B.45° C.60° D.75°
10.在Rt△ABC中,∠C=90°,若∠A=41°,则∠B的度数为( )
A.49° B.39° C.59° D.69°
二.填空题(共10小题,满分30分)
11.三角形三个内角度数之比是1:2:3,则此三角形是 三角形.
12.一副三角板如图放置,则∠1的度数为 .
13.如图,已知△ABC中,∠C=90°,则 .(请写出一条结论)
14.我们将一副三角尺按如图所示的位置摆放,则∠α﹣∠β= °.
15.如图,AD、AE分别是△ABC的高线和角平分线,若∠B=72°,∠DAE=16°,则∠C= .
16.如图,将一张三角形纸片ABC的一角(∠A)折叠,使得点A落在四边形BCDE的外部点A′的位置,且点A′与点C在直线AB的异侧,折痕为DE.已知∠C=90°,∠B=60°,若△A′DE的一边与BC平行,且∠ADE=m°,则m= .
17.如图所示,∠BAC的外角∠CAE等于100°,∠B=45°,则∠C的度数是 .
18.如图,两根竹竿AB和DB斜靠在墙CE上,量得∠CAB=33°,∠CDB=21°,则∠ABD的度数为 .
19.如图,直线DE∥BF,Rt△ABC中,∠ABC=90°,∠CBF=20°,则∠ADE= .
20.如图,在Rt△ABC中,∠BAC=90°,点D在BC上,过D作DF⊥BC交BA的延长线于F,连接AD,CF,若∠CFE=32°,∠ADB=45°,则∠B= .
三.解答题(共7小题,满分60分)
21.如图,在三角形ABC中,CD⊥AB于D,点E是AD上一点,FE⊥AB于E交AC于点H,点G是BC延长线上一点,连接FG,∠ACD+∠F=180°.
(1)求证:AC∥FG;
(2)若∠A=45°,∠BCD:∠ACD=2:3,求∠BCD的度数.
22.将一副学生三角板△OCD、△ODE按如图所示位置摆放,OC放置在直线AB上,求∠AOE的度数.
23.如图,在△ABC中,点E在AC上,点F在AB上,点G在BC上,且EF∥CD,∠1+∠2=180°.
(1)求证:GD∥CA;
(2)若CD平分∠ACB,DG平分∠CDB,且∠A=40°,求∠ACB的度数.
24.如图,在△ABC中,D,E分别是AB,AC边上的点(不与端点重合),连接DE,∠AED=∠B,DF平分∠BDE交射线BC于点F,连接EF.
(1)若∠C=50°,求∠BDE的度数;
(2)若∠ACB=∠DFE.
①求证:∠FED=∠FDE;
②延长FD至点G,连接EG,若∠A=2∠G,5∠FED﹣3∠DEG=180°,求∠G与∠C之间的数量关系.
25.阅读下面材料:
彤彤遇到这样一个问题:
已知:如图,AB∥CD,E为AB,CD之间一点,连接BE,DE,得到∠BED.求证:∠BED=∠B+∠D.
彤彤是这样做的:
过点E作EF∥AB,则有∠BEF=∠B.
∵AB∥CD,
∴EF∥CD.
∴∠FED=∠D.
∴∠BEF+∠FED=∠B+∠D.
即∠BED=∠B+∠D.
请你参考彤彤思考问题的方法,解决问题:
已知:直线a∥b,点AB在直线a上,点C,D在直线b上,连接AD,BC,BE平分∠ABC,DE平分∠ADC,且BE,DE所在的直线交于点E.
(1)如图1,当点B在点A的左侧时,若∠ABC=50°,∠ADC=60°,求∠BED的度数;
(2)如图2,当点B在点A的右侧时,设∠ABC=x°,∠ADC=y°,直接写出∠BED的度数(用含有x,y的式子表示).
26.【情景引入】
(1)如图1,BD、CD分别是△ABC的内角∠ABC、∠ACB的平分线,说明∠D=90°+的理由.
【深入探究】
(2)①如图2,BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线,∠D与∠A之间的等量关系是 ;
②如图3,BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线,探究∠D与∠A之间的等量关系,并说明理由.
【拓展应用】
(3)请用以上结论解决下列问题:如图4,在△ABC中,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ.
①∠A=80°,则∠F的度数为 ;
②∠F=n°,则∠A的度数为 .
27.新定义:在△ABC中,若存在最大内角是最小内角度数的n倍(n为大于1的正整数),则称△ABC为“n倍角三角形”.例如,在△ABC中,若∠A=90°,∠B=60°,则∠C=30°,因为∠A最大,∠C最小,且∠A=3∠C,所以△ABC为“3倍角三角形”.
(1)在△DEF中,若∠E=40°,∠F=60°,则△DEF为“ 倍角三角形”.
(2)如图,在△ABC中,∠C=36°,∠BAC、∠ABC的角平分线相交于点D,若△ABD为“6倍角三角形”,请求出∠ABD的度数.
参考答案
一.选择题(共10小题,满分30分)
1.解:如图
∠ACM=180°﹣∠ACN=180°﹣110°=70°,
∵EF∥MN,
∴∠ADB=∠ACM=70°,
∴∠ABF=180°﹣∠A﹣∠ADB=180°﹣90°﹣70°=20°.
故选:B.
2.解:由题意得:∠BCD=60°,∠ACB=45°,∠D=90°,
∴∠DCO=∠BCD﹣∠ACB=15°,
∵∠AOD是△DCO的外角,
∴∠AOD=∠D+∠DCO=105°.
故选:D.
3.解:∵∠C=90°,
∴∠CAB+∠B=90°,
∵DE⊥AB,
∴∠DEB=90°,
∴∠BDE+∠B=90°,
∴∠CAB=∠BDE,
∵∠BDE=56°,
∴∠CAB=56°,
∵AD平分∠CAB,
∴∠DAE=∠CAB=28°,
故选:B.
4.解:∵∠A+∠ADB+∠2=180°,
又∵∠A=55°,
∴∠ADB+∠2=125°,
∵∠1=∠2,
∴∠ADB+∠1=125°,
∴∠ADC=125°,
故选:C.
5.解:∵∠B=110°,∠C=30°,
∴∠A=180°﹣110°﹣30°=40°,
∵△DEF是由△ABC经过平移得到的,
∴AB∥DE,
∴∠AGD=∠A=40°,
∴∠DGH=180°﹣40°=140°,
故选:C.
6.解:在△ABC中,BD和CE是△ABC的两条角平分线,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∵∠A=52°,
∴∠BOC=180°﹣∠OBC﹣∠OCB
=180°﹣∠ABC﹣∠ACB
=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠A)
=180°﹣90°+×52°
=90°+26°
=116°.
故选:C.
7.解:∵∠A=35°,∠C=45°,
∴∠FDB=∠A+∠C=35°+45°=80°,
∵∠B=30°,
∴∠AFB=∠B+∠FDB=30°+80°=110°,
故选:D.
8.解:∵AD是∠BAC的平分线,
∴∠BAD=∠CAD=∠BAC,
∵∠ADC是△ABD的外角,∠ADC=65°,
∴∠B+∠BAC=65°,
∵∠C=90°,
∴∠B+∠BAC=90°,
∴∠BAC=50°,
故选:B.
9.解:∵AC∥EF,∠C=30°,
∴∠C=∠CBF=30°,
∵∠ABC=90°,
∴∠1=180°﹣∠ABC﹣∠CBF=180°﹣90°﹣30°=60°,
故选:C.
10.解:在Rt△ABC中,∠C=90°,∠A=41°,
∴∠B=180°﹣90°﹣41°=49°,
故选:A.
二.填空题(共10小题,满分30分)
11.解:设三角形的三个内角分别为k、2k、3k,
由题意得,k+2k+3k=180°,
解得k=30°,
∴3k=3×30°=90°,
∴此三角形是直角三角形.
故答案为:直角.
12.解:由题意得:∠ABC=90°﹣45°=45°,
∴∠1=∠ABC+∠A=45°+30°=75°,
故答案为:75°.
13.解:△ABC中,∠C=90°,
则∠A+∠B=90°(答案不唯一).
故答案为:∠A+∠B=90°(答案不唯一).
14.解:如图,
由图可得:∠CBD=45°,∠ABE=∠ADC=90°,∠E=60°,∠A=30°,
∴∠EBC=∠ABE﹣∠CBD=45°,
∴∠β=180°﹣∠EBC﹣∠E=75°,
∠α=∠A+∠ADC=120°,
∴∠α﹣∠β=45°.
故答案为:45°.
15.解:∵AD是高,∠B=72°,
∴∠BAD=90°﹣72°=18°,
∵∠DAE=16°,
∴∠BAE=18°+16°=34°,
∵AE是角平分线,
∴∠BAC=2∠BAE=68°,
∴∠C=180°﹣72°﹣68°=40°.
故答案为:40°.
16.解:当DA'∥BC时,如图,
∠A'DA=∠ACB=90°,
∵△ADE沿DE折叠到A'DE,
∴∠ADE=∠A'DE=∠ADA′=45°,
当EA'∥BC时,如图,连接AA',
∠2=∠ABC=60°,
∴∠A'AB=∠AA'E=30°,
∴∠DAA'=∠DA'A=60°,
∴△AA'D是等边三角形,
∴∠1=120°,
∵△ADE沿DE折叠到A'DE,
∴∠ADE=∠A'DE=∠ADA′=(180°﹣∠1)=30°,
综上所述,∠ADE的度数为:45°或30°.
故答案为:45或30.
17.解:由三角形的外角性质得:∠CAE=∠B+∠C,
∴∠C=∠CAE﹣∠B=100°﹣45°=55°;
故答案为:55°.
18.解:∵∠CAB是△ABD的外角,∠CAB=33°,∠CDB=21°,
∴∠ABD=∠CAB﹣∠CDB=12°,
故答案为:12°.
19.解:∵∠ABC=90°,∠CBF=20°,
∴∠ABF=90°﹣20°=70°,
∵DE∥BF,
∴∠ADE=∠ABF=70°,
故答案为:70°.
20.解:取CF的中点T,连接DT,AT,
∵∠BAC=90°,FD⊥BC,
∴∠CAF=∠CDF=90°,
∴AT=DT=CF,
∴TD=TC=TA,
∴∠TDA=∠TAD,∠TDC=∠TCD,
∵∠ADB=45°,
∴∠ADT+∠TDC=135°,
∴∠ATC=360°﹣2×135°=90°,
∴AT⊥CF,
∵CT=TF,
∴AC=AF,
∴∠AFC=45°,
∴∠BFD=45°﹣32°=13°,
∵∠BDF=90°,
∴∠B=90°﹣∠BFD=77°,
故答案为:77°.
三.解答题(共7小题,满分60分)
21.(1)证明:∵CD⊥AB,FE⊥AB,
∴∠AEH=∠ADC=90°,
∴EF∥DC,
∴∠ACD+∠CHE=180°,
∵∠ACD+∠F=180°,
∴∠F=∠CHE,
∴AC∥FG;
(2)解:∵∠BCD:∠ACD=2:3,
设∠BCD=2x,∠ACD=3x,
∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
即45°+3x=90°,
解得x=15°,
∴∠BCD=30°.
22.解:由题意得:∠CDO=45°,∠DOE=30°,∠OCD=90°,
∴∠AOD=∠CDO+∠OCD=135°,
∴∠AOE=∠AOD+∠DOE=165°.
23.证明:(1)∵EF∥CD,
∴∠1+∠3=180°.
∵∠1+∠2=180°,
∴∠2=∠3.
∴AC∥GD.
(2)∵CD平分∠ACB,DG平分∠CDB,
∴∠3=∠ACB,∠2=∠GDB=∠CDB.
∵∠CDB=∠A+∠3,∠2=∠3,
∴2∠3=∠A+∠3.
∴∠3=∠A=40°.
∴∠ACB=80°.
24.(1)解:方法一:∵在△ABC中,∠A+∠B+∠C=180°,
在△ADE中,∠ADE+∠AED+∠A=180°,∠AED=∠B,
∴∠C=∠ADE,
∵∠ADE+∠BDE=180°,
∴∠C+∠BDE=180°,
∵∠C=50°,
∴∠BDE=130°;
方法二:∵∠AED=∠B,∠CED+∠AED=180°,
∴∠CED+∠B=180°,
在四边形BCED中,∠B+∠C+∠CED+∠BDE=360°,
∴∠C+∠BDE=180°,
∵∠C=50°,
∴∠BDE=130°;
方法三:∵∠BDE=∠A+∠AED,∠AED=∠B,
∴∠BDE=∠A+∠B,
∵在△ABC中,∠C+∠B+∠A=180°,∠C=50°,
∴∠BDE=∠A+∠B=130°;
(2)①证明:由(1)得,∠C+∠BDE=180°,
即∠C+∠FDB+∠FDE=180°,
又在△FDE中,∠DFE+∠FED+∠FDE=180°,
∵∠C=∠DEFE,
∴∠FDB=∠FED,
∵DF平分∠BDE,
∴∠FDB=∠FDE=∠BDE,
∴∠FED=∠FDE;
②解:∵∠BDE=∠A+∠AED,∠FDE=∠G+∠GED,∠A=2∠G,∠FDE=∠BDE,
∴∠GED=∠AED,
设∠GDE=x,∠FED=y,
则∠FDE=∠FDB=y,∠G=y﹣x,
∴∠C=180°﹣2y,
∵5∠FED﹣3∠DEG=180°,
∴5y﹣3x=180°,
∴3y﹣3x=180°﹣2y,
即∠C=3y﹣3x,
∴∠C=3∠G.
25.解:(1)∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠ABC,∠CDE=∠ADC,
又∵∠ABC=50°,∠ADC=60°,
∴∠ABE=25°,∠CDE=30°,
∴∠BED=∠ABE+∠CDE=55°;
(2)过点E作EF∥AB,如图所示:
则∠ABE+∠BEF=180°,
∴∠BEF=180°﹣∠ABE,
∵AB∥CD,
∴EF∥CD,
∴∠FED=∠EDC,
∴∠BED=180°﹣∠ABE+∠EDC,
∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠ABC,∠CDE=∠ADC,
∵∠ABC=x°,∠ADC=y°,
∴∠ABE=,∠CDE=,
∴∠BED=180°﹣+.
26.解:(1)∵BD、CD分别是∠ABC、∠ACB的平分线,
∴∠1=∠ABC,∠2=∠ACB,
∴∠1+∠2=(∠ABC+∠ACB),
∵∠A+∠ABC+∠ACB=180°,∠1+∠2+∠D=180°,
∴∠D=180°﹣∠1﹣∠2=180°﹣(∠ABC+∠ACB),
∴∠D=90°+∠A;
(2)①∠D与∠A之间的等量关系是:∠D=90°﹣∠A,理由如下:
∵BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线,
∴∠EBD=∠DBC,∠BCD=∠DCF,
∵∠DBC+∠DCB+∠D=180°,∠A+∠ABC+∠ACB=180°,∠ABC=180°﹣2∠DBC,∠ACB=180°﹣2∠DCB,
∴∠A+180°﹣2∠DBC+180°﹣2∠DCB=180°,∠DBC+∠DCB=180°﹣∠D,
∴∠A﹣2(∠DBC+∠DCB)=﹣180°,
∴∠A﹣2(180°﹣∠D)=﹣180°,
∴∠A+2∠D=180°,
∴∠D=90°﹣∠A,
故答案为:∠D=90°﹣∠A;
②∠D与∠A之间的等量关系是:∠D=∠A,理由如下:
∵BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线,
∵∠DCE=∠DBC+∠D,∠A+2∠DBC=2∠DCE,
∴∠A+2∠DBC=2∠DBC+2∠D,
∴∠A=2∠D,
∴:∠D=∠A;
(3)①由(1)知:∠D=90°+∠A,
∵∠A=80°,
∴∠D=130°,
∴∠DBC+∠DCB=50°,
∴∠MBC+∠NCB=360°﹣50°=310°,
∵BE、CE分别平分∠MBC、∠BCN,
∴∠CBE+∠BCE=(∠MBC+∠NCB)=155°,
∴∠E=180°﹣155°=25°,
由(2)②知:∠F=∠E,
∴∠F=∠E=12.5°,
故答案为:12.5°;
②由(2)②知:∠F=∠E,
∵∠F=n°,
∴∠E=2∠F=2n°,
∵∠E+∠CBE+∠BCE=180°,
∴∠CBE+∠BCE=180°﹣∠E=180°﹣2n°,
∵BE、CE分别平分∠MBC、∠BCN,
∴∠MBE=∠CBE,∠NCE=∠BCE,
∵∠MBC=∠MBE+∠CBE=2∠CBE,∠NCB=∠NCE+∠BCE=2∠BCE,
∴∠MBC+∠NCB=2(∠CBE+∠BCE)=360°﹣4n°,
∵∠DBC=180°﹣∠MBC,∠DCB=180°﹣∠NCB,
∴∠DBC+∠DCB=180°﹣∠MBC+180°﹣∠NCB=360°﹣(∠MBC+∠NCB)=4n°,
∵∠DBC+∠DCB+∠D=180°,
∴∠D=180°﹣4n°,
由(1)知:∠D=90°+∠A,
∴∠A=180°﹣8n°,
故答案为:180°﹣8n°.
27.解:(1)在△DEF中,∠E=40°,∠F=60°,
则∠D=180°﹣∠E﹣∠F=80°,
∴∠D=2∠E,
∴△DEF为“2倍角三角形”,
故答案为:2;
(2)∵∠C=36°,
∴∠BAC+∠ABC=180°﹣36°=144°,
∵∠BAC、∠ABC的角平分线相交于点D,
∴∠DAB=∠BAC,∠DBA=∠ABC,
∴∠DAB+∠DBA=×144°=72°,
∴∠ADB=180°﹣72°=108°,
∵△ABD为“6倍角三角形”,
∴∠ADB=6∠ABD或∠ADB=6∠BAD,
当∠ADB=6∠ABD时,∠ABD=18°,
当∠ADB=6∠BAD时,∠BAD=18°,则∠ABD=180°﹣108°﹣18°=54°,
综上所述,∠ABD的度数为18°或54°.
一.选择题(共10小题,满分30分)
1.如图,在Rt△ABC中,∠A=90°,点B在直线EF上,点C在直线MN上,且直线EF∥MN,∠ACN=110°,则∠ABF的度数为( )
A.10° B.20° C.30° D.160°
2.如图,将一副直角三角板按如图所示的位置放置,则∠AOD的度数是( )
A.85° B.90° C.75° D.105°
3.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB,若∠BDE=56°,则∠DAE的度数为( )度.
A.23 B.28 C.52 D.56
4.如图所示,在四边形ABCD中,BD是它的一条对角线,若∠1=∠2,∠A=55°,则∠ADC=( )
A.110° B.115° C.125° D.135°
如图,△DEF是由△ABC经过平移得到的,已知∠B=110°,∠C=30°,则∠DGH的度数为( )
A.30° B.110° C.140° D.150°
6.如图,在△ABC中,BD和CE是△ABC的两条角平分线.若∠A=52°,则∠BOC的度数为( )
A.64° B.106° C.116° D.128°
7.如图,点D、E分别在线段BC、AC上,连接AD、BE.若∠A=35°,∠B=30°,∠C=45°,则∠AFB的大小为( )
A.75° B.80° C.100° D.110°
8.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,若∠ADC=65°,则∠BAC的大小为( )
A.35° B.50° C.65° D.70°
9.如图,把一块三角板ABC的直角顶点B放在直线EF上,∠C=30°,AC∥EF,则∠1=( )
A.30° B.45° C.60° D.75°
10.在Rt△ABC中,∠C=90°,若∠A=41°,则∠B的度数为( )
A.49° B.39° C.59° D.69°
二.填空题(共10小题,满分30分)
11.三角形三个内角度数之比是1:2:3,则此三角形是 三角形.
12.一副三角板如图放置,则∠1的度数为 .
13.如图,已知△ABC中,∠C=90°,则 .(请写出一条结论)
14.我们将一副三角尺按如图所示的位置摆放,则∠α﹣∠β= °.
15.如图,AD、AE分别是△ABC的高线和角平分线,若∠B=72°,∠DAE=16°,则∠C= .
16.如图,将一张三角形纸片ABC的一角(∠A)折叠,使得点A落在四边形BCDE的外部点A′的位置,且点A′与点C在直线AB的异侧,折痕为DE.已知∠C=90°,∠B=60°,若△A′DE的一边与BC平行,且∠ADE=m°,则m= .
17.如图所示,∠BAC的外角∠CAE等于100°,∠B=45°,则∠C的度数是 .
18.如图,两根竹竿AB和DB斜靠在墙CE上,量得∠CAB=33°,∠CDB=21°,则∠ABD的度数为 .
19.如图,直线DE∥BF,Rt△ABC中,∠ABC=90°,∠CBF=20°,则∠ADE= .
20.如图,在Rt△ABC中,∠BAC=90°,点D在BC上,过D作DF⊥BC交BA的延长线于F,连接AD,CF,若∠CFE=32°,∠ADB=45°,则∠B= .
三.解答题(共7小题,满分60分)
21.如图,在三角形ABC中,CD⊥AB于D,点E是AD上一点,FE⊥AB于E交AC于点H,点G是BC延长线上一点,连接FG,∠ACD+∠F=180°.
(1)求证:AC∥FG;
(2)若∠A=45°,∠BCD:∠ACD=2:3,求∠BCD的度数.
22.将一副学生三角板△OCD、△ODE按如图所示位置摆放,OC放置在直线AB上,求∠AOE的度数.
23.如图,在△ABC中,点E在AC上,点F在AB上,点G在BC上,且EF∥CD,∠1+∠2=180°.
(1)求证:GD∥CA;
(2)若CD平分∠ACB,DG平分∠CDB,且∠A=40°,求∠ACB的度数.
24.如图,在△ABC中,D,E分别是AB,AC边上的点(不与端点重合),连接DE,∠AED=∠B,DF平分∠BDE交射线BC于点F,连接EF.
(1)若∠C=50°,求∠BDE的度数;
(2)若∠ACB=∠DFE.
①求证:∠FED=∠FDE;
②延长FD至点G,连接EG,若∠A=2∠G,5∠FED﹣3∠DEG=180°,求∠G与∠C之间的数量关系.
25.阅读下面材料:
彤彤遇到这样一个问题:
已知:如图,AB∥CD,E为AB,CD之间一点,连接BE,DE,得到∠BED.求证:∠BED=∠B+∠D.
彤彤是这样做的:
过点E作EF∥AB,则有∠BEF=∠B.
∵AB∥CD,
∴EF∥CD.
∴∠FED=∠D.
∴∠BEF+∠FED=∠B+∠D.
即∠BED=∠B+∠D.
请你参考彤彤思考问题的方法,解决问题:
已知:直线a∥b,点AB在直线a上,点C,D在直线b上,连接AD,BC,BE平分∠ABC,DE平分∠ADC,且BE,DE所在的直线交于点E.
(1)如图1,当点B在点A的左侧时,若∠ABC=50°,∠ADC=60°,求∠BED的度数;
(2)如图2,当点B在点A的右侧时,设∠ABC=x°,∠ADC=y°,直接写出∠BED的度数(用含有x,y的式子表示).
26.【情景引入】
(1)如图1,BD、CD分别是△ABC的内角∠ABC、∠ACB的平分线,说明∠D=90°+的理由.
【深入探究】
(2)①如图2,BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线,∠D与∠A之间的等量关系是 ;
②如图3,BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线,探究∠D与∠A之间的等量关系,并说明理由.
【拓展应用】
(3)请用以上结论解决下列问题:如图4,在△ABC中,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ.
①∠A=80°,则∠F的度数为 ;
②∠F=n°,则∠A的度数为 .
27.新定义:在△ABC中,若存在最大内角是最小内角度数的n倍(n为大于1的正整数),则称△ABC为“n倍角三角形”.例如,在△ABC中,若∠A=90°,∠B=60°,则∠C=30°,因为∠A最大,∠C最小,且∠A=3∠C,所以△ABC为“3倍角三角形”.
(1)在△DEF中,若∠E=40°,∠F=60°,则△DEF为“ 倍角三角形”.
(2)如图,在△ABC中,∠C=36°,∠BAC、∠ABC的角平分线相交于点D,若△ABD为“6倍角三角形”,请求出∠ABD的度数.
参考答案
一.选择题(共10小题,满分30分)
1.解:如图
∠ACM=180°﹣∠ACN=180°﹣110°=70°,
∵EF∥MN,
∴∠ADB=∠ACM=70°,
∴∠ABF=180°﹣∠A﹣∠ADB=180°﹣90°﹣70°=20°.
故选:B.
2.解:由题意得:∠BCD=60°,∠ACB=45°,∠D=90°,
∴∠DCO=∠BCD﹣∠ACB=15°,
∵∠AOD是△DCO的外角,
∴∠AOD=∠D+∠DCO=105°.
故选:D.
3.解:∵∠C=90°,
∴∠CAB+∠B=90°,
∵DE⊥AB,
∴∠DEB=90°,
∴∠BDE+∠B=90°,
∴∠CAB=∠BDE,
∵∠BDE=56°,
∴∠CAB=56°,
∵AD平分∠CAB,
∴∠DAE=∠CAB=28°,
故选:B.
4.解:∵∠A+∠ADB+∠2=180°,
又∵∠A=55°,
∴∠ADB+∠2=125°,
∵∠1=∠2,
∴∠ADB+∠1=125°,
∴∠ADC=125°,
故选:C.
5.解:∵∠B=110°,∠C=30°,
∴∠A=180°﹣110°﹣30°=40°,
∵△DEF是由△ABC经过平移得到的,
∴AB∥DE,
∴∠AGD=∠A=40°,
∴∠DGH=180°﹣40°=140°,
故选:C.
6.解:在△ABC中,BD和CE是△ABC的两条角平分线,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∵∠A=52°,
∴∠BOC=180°﹣∠OBC﹣∠OCB
=180°﹣∠ABC﹣∠ACB
=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠A)
=180°﹣90°+×52°
=90°+26°
=116°.
故选:C.
7.解:∵∠A=35°,∠C=45°,
∴∠FDB=∠A+∠C=35°+45°=80°,
∵∠B=30°,
∴∠AFB=∠B+∠FDB=30°+80°=110°,
故选:D.
8.解:∵AD是∠BAC的平分线,
∴∠BAD=∠CAD=∠BAC,
∵∠ADC是△ABD的外角,∠ADC=65°,
∴∠B+∠BAC=65°,
∵∠C=90°,
∴∠B+∠BAC=90°,
∴∠BAC=50°,
故选:B.
9.解:∵AC∥EF,∠C=30°,
∴∠C=∠CBF=30°,
∵∠ABC=90°,
∴∠1=180°﹣∠ABC﹣∠CBF=180°﹣90°﹣30°=60°,
故选:C.
10.解:在Rt△ABC中,∠C=90°,∠A=41°,
∴∠B=180°﹣90°﹣41°=49°,
故选:A.
二.填空题(共10小题,满分30分)
11.解:设三角形的三个内角分别为k、2k、3k,
由题意得,k+2k+3k=180°,
解得k=30°,
∴3k=3×30°=90°,
∴此三角形是直角三角形.
故答案为:直角.
12.解:由题意得:∠ABC=90°﹣45°=45°,
∴∠1=∠ABC+∠A=45°+30°=75°,
故答案为:75°.
13.解:△ABC中,∠C=90°,
则∠A+∠B=90°(答案不唯一).
故答案为:∠A+∠B=90°(答案不唯一).
14.解:如图,
由图可得:∠CBD=45°,∠ABE=∠ADC=90°,∠E=60°,∠A=30°,
∴∠EBC=∠ABE﹣∠CBD=45°,
∴∠β=180°﹣∠EBC﹣∠E=75°,
∠α=∠A+∠ADC=120°,
∴∠α﹣∠β=45°.
故答案为:45°.
15.解:∵AD是高,∠B=72°,
∴∠BAD=90°﹣72°=18°,
∵∠DAE=16°,
∴∠BAE=18°+16°=34°,
∵AE是角平分线,
∴∠BAC=2∠BAE=68°,
∴∠C=180°﹣72°﹣68°=40°.
故答案为:40°.
16.解:当DA'∥BC时,如图,
∠A'DA=∠ACB=90°,
∵△ADE沿DE折叠到A'DE,
∴∠ADE=∠A'DE=∠ADA′=45°,
当EA'∥BC时,如图,连接AA',
∠2=∠ABC=60°,
∴∠A'AB=∠AA'E=30°,
∴∠DAA'=∠DA'A=60°,
∴△AA'D是等边三角形,
∴∠1=120°,
∵△ADE沿DE折叠到A'DE,
∴∠ADE=∠A'DE=∠ADA′=(180°﹣∠1)=30°,
综上所述,∠ADE的度数为:45°或30°.
故答案为:45或30.
17.解:由三角形的外角性质得:∠CAE=∠B+∠C,
∴∠C=∠CAE﹣∠B=100°﹣45°=55°;
故答案为:55°.
18.解:∵∠CAB是△ABD的外角,∠CAB=33°,∠CDB=21°,
∴∠ABD=∠CAB﹣∠CDB=12°,
故答案为:12°.
19.解:∵∠ABC=90°,∠CBF=20°,
∴∠ABF=90°﹣20°=70°,
∵DE∥BF,
∴∠ADE=∠ABF=70°,
故答案为:70°.
20.解:取CF的中点T,连接DT,AT,
∵∠BAC=90°,FD⊥BC,
∴∠CAF=∠CDF=90°,
∴AT=DT=CF,
∴TD=TC=TA,
∴∠TDA=∠TAD,∠TDC=∠TCD,
∵∠ADB=45°,
∴∠ADT+∠TDC=135°,
∴∠ATC=360°﹣2×135°=90°,
∴AT⊥CF,
∵CT=TF,
∴AC=AF,
∴∠AFC=45°,
∴∠BFD=45°﹣32°=13°,
∵∠BDF=90°,
∴∠B=90°﹣∠BFD=77°,
故答案为:77°.
三.解答题(共7小题,满分60分)
21.(1)证明:∵CD⊥AB,FE⊥AB,
∴∠AEH=∠ADC=90°,
∴EF∥DC,
∴∠ACD+∠CHE=180°,
∵∠ACD+∠F=180°,
∴∠F=∠CHE,
∴AC∥FG;
(2)解:∵∠BCD:∠ACD=2:3,
设∠BCD=2x,∠ACD=3x,
∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
即45°+3x=90°,
解得x=15°,
∴∠BCD=30°.
22.解:由题意得:∠CDO=45°,∠DOE=30°,∠OCD=90°,
∴∠AOD=∠CDO+∠OCD=135°,
∴∠AOE=∠AOD+∠DOE=165°.
23.证明:(1)∵EF∥CD,
∴∠1+∠3=180°.
∵∠1+∠2=180°,
∴∠2=∠3.
∴AC∥GD.
(2)∵CD平分∠ACB,DG平分∠CDB,
∴∠3=∠ACB,∠2=∠GDB=∠CDB.
∵∠CDB=∠A+∠3,∠2=∠3,
∴2∠3=∠A+∠3.
∴∠3=∠A=40°.
∴∠ACB=80°.
24.(1)解:方法一:∵在△ABC中,∠A+∠B+∠C=180°,
在△ADE中,∠ADE+∠AED+∠A=180°,∠AED=∠B,
∴∠C=∠ADE,
∵∠ADE+∠BDE=180°,
∴∠C+∠BDE=180°,
∵∠C=50°,
∴∠BDE=130°;
方法二:∵∠AED=∠B,∠CED+∠AED=180°,
∴∠CED+∠B=180°,
在四边形BCED中,∠B+∠C+∠CED+∠BDE=360°,
∴∠C+∠BDE=180°,
∵∠C=50°,
∴∠BDE=130°;
方法三:∵∠BDE=∠A+∠AED,∠AED=∠B,
∴∠BDE=∠A+∠B,
∵在△ABC中,∠C+∠B+∠A=180°,∠C=50°,
∴∠BDE=∠A+∠B=130°;
(2)①证明:由(1)得,∠C+∠BDE=180°,
即∠C+∠FDB+∠FDE=180°,
又在△FDE中,∠DFE+∠FED+∠FDE=180°,
∵∠C=∠DEFE,
∴∠FDB=∠FED,
∵DF平分∠BDE,
∴∠FDB=∠FDE=∠BDE,
∴∠FED=∠FDE;
②解:∵∠BDE=∠A+∠AED,∠FDE=∠G+∠GED,∠A=2∠G,∠FDE=∠BDE,
∴∠GED=∠AED,
设∠GDE=x,∠FED=y,
则∠FDE=∠FDB=y,∠G=y﹣x,
∴∠C=180°﹣2y,
∵5∠FED﹣3∠DEG=180°,
∴5y﹣3x=180°,
∴3y﹣3x=180°﹣2y,
即∠C=3y﹣3x,
∴∠C=3∠G.
25.解:(1)∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠ABC,∠CDE=∠ADC,
又∵∠ABC=50°,∠ADC=60°,
∴∠ABE=25°,∠CDE=30°,
∴∠BED=∠ABE+∠CDE=55°;
(2)过点E作EF∥AB,如图所示:
则∠ABE+∠BEF=180°,
∴∠BEF=180°﹣∠ABE,
∵AB∥CD,
∴EF∥CD,
∴∠FED=∠EDC,
∴∠BED=180°﹣∠ABE+∠EDC,
∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠ABC,∠CDE=∠ADC,
∵∠ABC=x°,∠ADC=y°,
∴∠ABE=,∠CDE=,
∴∠BED=180°﹣+.
26.解:(1)∵BD、CD分别是∠ABC、∠ACB的平分线,
∴∠1=∠ABC,∠2=∠ACB,
∴∠1+∠2=(∠ABC+∠ACB),
∵∠A+∠ABC+∠ACB=180°,∠1+∠2+∠D=180°,
∴∠D=180°﹣∠1﹣∠2=180°﹣(∠ABC+∠ACB),
∴∠D=90°+∠A;
(2)①∠D与∠A之间的等量关系是:∠D=90°﹣∠A,理由如下:
∵BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线,
∴∠EBD=∠DBC,∠BCD=∠DCF,
∵∠DBC+∠DCB+∠D=180°,∠A+∠ABC+∠ACB=180°,∠ABC=180°﹣2∠DBC,∠ACB=180°﹣2∠DCB,
∴∠A+180°﹣2∠DBC+180°﹣2∠DCB=180°,∠DBC+∠DCB=180°﹣∠D,
∴∠A﹣2(∠DBC+∠DCB)=﹣180°,
∴∠A﹣2(180°﹣∠D)=﹣180°,
∴∠A+2∠D=180°,
∴∠D=90°﹣∠A,
故答案为:∠D=90°﹣∠A;
②∠D与∠A之间的等量关系是:∠D=∠A,理由如下:
∵BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线,
∵∠DCE=∠DBC+∠D,∠A+2∠DBC=2∠DCE,
∴∠A+2∠DBC=2∠DBC+2∠D,
∴∠A=2∠D,
∴:∠D=∠A;
(3)①由(1)知:∠D=90°+∠A,
∵∠A=80°,
∴∠D=130°,
∴∠DBC+∠DCB=50°,
∴∠MBC+∠NCB=360°﹣50°=310°,
∵BE、CE分别平分∠MBC、∠BCN,
∴∠CBE+∠BCE=(∠MBC+∠NCB)=155°,
∴∠E=180°﹣155°=25°,
由(2)②知:∠F=∠E,
∴∠F=∠E=12.5°,
故答案为:12.5°;
②由(2)②知:∠F=∠E,
∵∠F=n°,
∴∠E=2∠F=2n°,
∵∠E+∠CBE+∠BCE=180°,
∴∠CBE+∠BCE=180°﹣∠E=180°﹣2n°,
∵BE、CE分别平分∠MBC、∠BCN,
∴∠MBE=∠CBE,∠NCE=∠BCE,
∵∠MBC=∠MBE+∠CBE=2∠CBE,∠NCB=∠NCE+∠BCE=2∠BCE,
∴∠MBC+∠NCB=2(∠CBE+∠BCE)=360°﹣4n°,
∵∠DBC=180°﹣∠MBC,∠DCB=180°﹣∠NCB,
∴∠DBC+∠DCB=180°﹣∠MBC+180°﹣∠NCB=360°﹣(∠MBC+∠NCB)=4n°,
∵∠DBC+∠DCB+∠D=180°,
∴∠D=180°﹣4n°,
由(1)知:∠D=90°+∠A,
∴∠A=180°﹣8n°,
故答案为:180°﹣8n°.
27.解:(1)在△DEF中,∠E=40°,∠F=60°,
则∠D=180°﹣∠E﹣∠F=80°,
∴∠D=2∠E,
∴△DEF为“2倍角三角形”,
故答案为:2;
(2)∵∠C=36°,
∴∠BAC+∠ABC=180°﹣36°=144°,
∵∠BAC、∠ABC的角平分线相交于点D,
∴∠DAB=∠BAC,∠DBA=∠ABC,
∴∠DAB+∠DBA=×144°=72°,
∴∠ADB=180°﹣72°=108°,
∵△ABD为“6倍角三角形”,
∴∠ADB=6∠ABD或∠ADB=6∠BAD,
当∠ADB=6∠ABD时,∠ABD=18°,
当∠ADB=6∠BAD时,∠BAD=18°,则∠ABD=180°﹣108°﹣18°=54°,
综上所述,∠ABD的度数为18°或54°.
