第12章 一次函数小结(2)一次函数的图象及其性质 课件(共27张PPT)
文档属性
| 名称 | 第12章 一次函数小结(2)一次函数的图象及其性质 课件(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
沪科版 八年级上册
第12章 一次函数期小结(2)
一次函数图象和性质
本课是在学习完函数的概念及其表示法,学习了一次函数的有关知识后,进行的全章内容的回顾与复习活动,整理全章的知识结构,概括函数研究的思想方法:抽象的思想、模型的思想、对应的思想、数形结合的思想.
课件说明
特别地,当b=0时,一次函数y=kx+b就成为 y= (k≠0),这时,y叫做x的 函数.
形如 (k,b是常数,k≠0)的函数叫做的一次函数.
y=kx+b
kx
1.一次函数的定义
正比例
知识要点
当k 时,y随x的增大而增大,
当k 时,y随x的增大而减小.
3.一次函数的性质
>0
<0
一次函数y=kx+b(k,b是常数,k≠0)的图象是一条 . 特别地,正比例函数
y=kx(k≠0)的图象是一条过 的直线.
直线
原点
2.一次函数的图象
(1)当 b>0 时, y=kx图象沿y轴向 平
移 个单位,得到y=kx+b 的图象;
上
下
4.一次函数y=kx+b与正比例函数y=kx图象的关系
一次函数 y=kx+b 的图象可以由正比例函数
y=kx图象平移得到.
(2)当 b<0 时,y=kx图象沿y轴向 平
移 个单位,得到y=kx+b 的图象.
b
| b |
(1)设所求的一次函数解析式为_________,其中k,b是待确定的常数.
(2)把两对已知的自变量与函数的对应值分别代入________,得到关于k,b的______________ .
(3)解这个关于k,b的______________,求出____ 的值.
(4)把求得的k,b的值代入_________,就得到所求的一次函数解析式.
5. 确定一次函数解析式的方法
y=kx+b
y=kx+b
二元一次方程组
二元一次方程组
k,b
y=kx+b
两对自变量与函数的对应值给出的方式有:
(1)以两组数给出;
(2)以两个点的坐标给出;
(3)隐含在函数的图象中.
当x = 20时,y = 900;当x = 30时,y = 1200.
A(-1,0)、B(2,-3)两点在一次函数y=kx+b图象上.
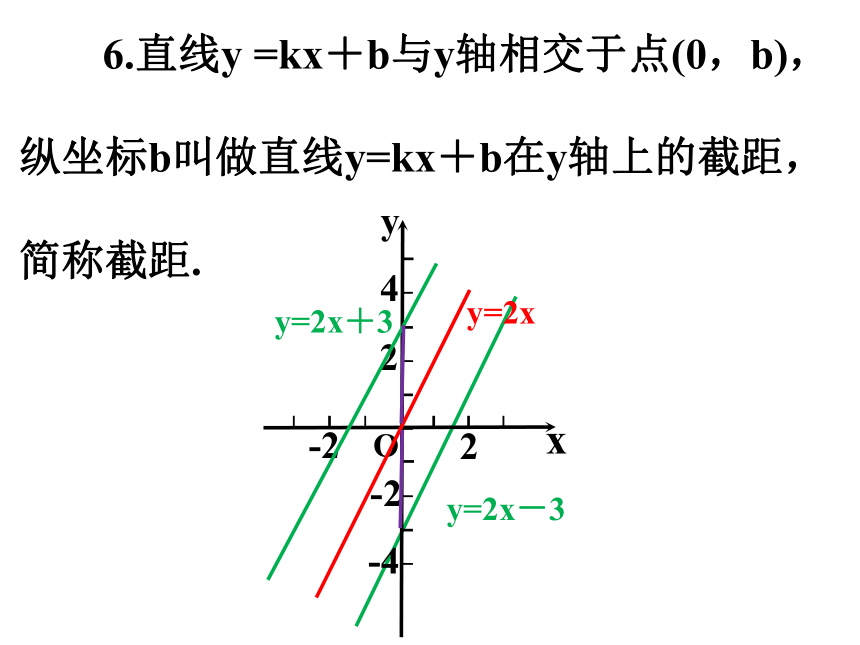
6.直线y =kx+b与y轴相交于点(0,b),
纵坐标b叫做直线y=kx+b在y轴上的截距,
简称截距.
y=2x-3
4
2
-2
-2
2
x
y
O
-4
y=2x
y=2x+3
例1.已知函数y=(2m+3)x+m-1,
(1)若函数图象经过原点,求m的值;
(2)若函数图象在y轴上的截距为-3,求m的值;
(3)若函数图象平行于直线y=x+1,求m的值;
(4)若该函数的值y随自变量x的增大而减小,求m
的取值范围.
典型例析
例1.已知函数y=(2m+3)x+m-1,
(1)若函数图象经过原点,求m的值;
(2)若函数图象在y轴上的截距为-3,求m的值;
典型例析
解:(1)
∵若函数图象经过原点,
∴ m-1=0,
∴ m=1.
(2) ∵函数图象在y轴上的截距为-3,
∴ m-1=-3,
∴ m=-2.
例1.已知函数y=(2m+3)x+m-1,
(3)若函数图象平行于直线y=x+1,求m的值;
(4)若该函数的值y随自变量x的增大而减小,
求m 的取值范围.
典型例析
(3) ∵函数图象平行于直线y=x+1,
∴ 2m+3=1,
∴ m= -1.
(4) ∵该函数的值y随自变量x的增大而减小,
∴ 2m+3= <0,
∴ m= - .
3
2
例2.已知:正比例函数和一次函数的图象经过点A(1,2),且一次函数的图象与x轴交于点B (4,) 求正比例函数和一次函数的表达式.
∴正比例函数的表达式为:
y=2x.
∵正比例函数的图象经过点A(1,2) ,
解:
∴ k=2
设正比例函数的表达式为:
y=kx.
例2.已知:正比例函数和一次函数的图象经过点A(1,2),且一次函数的图象与x轴交于点B (4,) 求正比例函数和一次函数的表达式.
∴一次函数的表达式为:
∵一次例函数的图象经过点A(1,2), B(4,0) ,
解:
设一次函数的表达式为:
y=kx+b.
∴
4k+b=0
k= -
b=
k+b=2
∴
2
3
8
3
y= - x+ .
2
3
8
3
(2)若一次函数y=kx+b的图象与x轴的交点
为A(a,0),求a的值.
12.已知:一次函数y=kx+b的图象经过M(0,2),
N(1,3) 两点.(1)求k,b的值;
∴一次函数的解析式为:
y=x+2
(2)∵k=1,b=2
把y=0,x=a,代入y=x+2,得
a+2=0,
∴a= -2.
∴
函数点A(1,3) ,
解:
1.已知正比例函数y=kx(k≠0) 的图象经过点(-2,1),则这个正比例函数的解析式为( ).
A.y=2x B.y=-2x
C.y= x D.y=- x
1
2
1
2
D
练习巩固
2.P1(x1,y1),P2(x2,y2)是正比例函数y=-x图象上的两点,下列判断中,正确的是( ).
A.y1>y2 B.y1<y2
C.当x1<x2时,y1<y2 D.当x1<x2时,y1>y2
D
3.如果一个正比例函数的图象经过不同象限的两点A(2,m),B(n,3),那么一定有( )
A.m>0,n>0 B.m>0,n<0
C.m<0,n>0 D.m<0,n<0
D
4.下列函数中,y随x的增大而减小的函数是( )
A.y=2x+8 B.y=-2+4x
C.y=-2x+8 D.y=4x
C
6.一次函数y=mx+|m-1|的图象过点(0,2),且y随x的增大而增大,则m的值为( ).
A.-1 B.3 C.1 D.-1或3
B
5.若一次函数 y=(k-3)x+5,且y随x的增大而减小,则k的取值范围是( ).
A.k>0
B. k<0
C.k>3
D.k<3
C
7.把直线y=2x+3向上平移4个单位,所得
直线是函数__________的图象.
y=2x+7
8.把直线y=-2x-2向下移2个单位,
所得直线是函数__________的图象.
y=-2x-4
9.函数y=-2x-3在y轴上的截距是____.
-3
10.函数y=- x + 在y轴上的截距是____.
3
2
4
3
4
3
11.已知直线y=kx+b与直线y=2x平行,且
在y轴上的截距为-5,则此直线的解析
式为 .
y=2x-5
12.若一条直线经过点 (-1 ,1)和点 (1, 5 ),则这条直线与 x轴的交点坐标是 .
(- ,0)
3
2
-k+b=1
k+b=5
k=2
b=3
y=kx+b
y=2x+3
0=2x+3
(2)若一次函数y=kx+b的图象与x轴的交点
为A(a,0),求a的值.
13.已知:一次函数y=kx+b的图象经过M(0,2),
N(1,3) 两点.(1)求k,b的值;
∴一次函数的解析式为:
y=x+2
(2)∵k=1,b=2
把y=0,x=a,代入y=x+2,得
a+2=0,
∴a= -2.
∴
∴
∵一次函数y=kx+b过(0,2),(1,3)点,
解:(1)
b=2
k+b=3
k=1
b=2
(1)什么叫一次函数?正比例函数与一次函数有什么关系?我们主要研究了一次函数的哪些性质?
(2)我们是怎样研究一次函数性质的?
课堂小结
今天作业
课本P48页第9题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 八年级上册
第12章 一次函数期小结(2)
一次函数图象和性质
本课是在学习完函数的概念及其表示法,学习了一次函数的有关知识后,进行的全章内容的回顾与复习活动,整理全章的知识结构,概括函数研究的思想方法:抽象的思想、模型的思想、对应的思想、数形结合的思想.
课件说明
特别地,当b=0时,一次函数y=kx+b就成为 y= (k≠0),这时,y叫做x的 函数.
形如 (k,b是常数,k≠0)的函数叫做的一次函数.
y=kx+b
kx
1.一次函数的定义
正比例
知识要点
当k 时,y随x的增大而增大,
当k 时,y随x的增大而减小.
3.一次函数的性质
>0
<0
一次函数y=kx+b(k,b是常数,k≠0)的图象是一条 . 特别地,正比例函数
y=kx(k≠0)的图象是一条过 的直线.
直线
原点
2.一次函数的图象
(1)当 b>0 时, y=kx图象沿y轴向 平
移 个单位,得到y=kx+b 的图象;
上
下
4.一次函数y=kx+b与正比例函数y=kx图象的关系
一次函数 y=kx+b 的图象可以由正比例函数
y=kx图象平移得到.
(2)当 b<0 时,y=kx图象沿y轴向 平
移 个单位,得到y=kx+b 的图象.
b
| b |
(1)设所求的一次函数解析式为_________,其中k,b是待确定的常数.
(2)把两对已知的自变量与函数的对应值分别代入________,得到关于k,b的______________ .
(3)解这个关于k,b的______________,求出____ 的值.
(4)把求得的k,b的值代入_________,就得到所求的一次函数解析式.
5. 确定一次函数解析式的方法
y=kx+b
y=kx+b
二元一次方程组
二元一次方程组
k,b
y=kx+b
两对自变量与函数的对应值给出的方式有:
(1)以两组数给出;
(2)以两个点的坐标给出;
(3)隐含在函数的图象中.
当x = 20时,y = 900;当x = 30时,y = 1200.
A(-1,0)、B(2,-3)两点在一次函数y=kx+b图象上.
6.直线y =kx+b与y轴相交于点(0,b),
纵坐标b叫做直线y=kx+b在y轴上的截距,
简称截距.
y=2x-3
4
2
-2
-2
2
x
y
O
-4
y=2x
y=2x+3
例1.已知函数y=(2m+3)x+m-1,
(1)若函数图象经过原点,求m的值;
(2)若函数图象在y轴上的截距为-3,求m的值;
(3)若函数图象平行于直线y=x+1,求m的值;
(4)若该函数的值y随自变量x的增大而减小,求m
的取值范围.
典型例析
例1.已知函数y=(2m+3)x+m-1,
(1)若函数图象经过原点,求m的值;
(2)若函数图象在y轴上的截距为-3,求m的值;
典型例析
解:(1)
∵若函数图象经过原点,
∴ m-1=0,
∴ m=1.
(2) ∵函数图象在y轴上的截距为-3,
∴ m-1=-3,
∴ m=-2.
例1.已知函数y=(2m+3)x+m-1,
(3)若函数图象平行于直线y=x+1,求m的值;
(4)若该函数的值y随自变量x的增大而减小,
求m 的取值范围.
典型例析
(3) ∵函数图象平行于直线y=x+1,
∴ 2m+3=1,
∴ m= -1.
(4) ∵该函数的值y随自变量x的增大而减小,
∴ 2m+3= <0,
∴ m= - .
3
2
例2.已知:正比例函数和一次函数的图象经过点A(1,2),且一次函数的图象与x轴交于点B (4,) 求正比例函数和一次函数的表达式.
∴正比例函数的表达式为:
y=2x.
∵正比例函数的图象经过点A(1,2) ,
解:
∴ k=2
设正比例函数的表达式为:
y=kx.
例2.已知:正比例函数和一次函数的图象经过点A(1,2),且一次函数的图象与x轴交于点B (4,) 求正比例函数和一次函数的表达式.
∴一次函数的表达式为:
∵一次例函数的图象经过点A(1,2), B(4,0) ,
解:
设一次函数的表达式为:
y=kx+b.
∴
4k+b=0
k= -
b=
k+b=2
∴
2
3
8
3
y= - x+ .
2
3
8
3
(2)若一次函数y=kx+b的图象与x轴的交点
为A(a,0),求a的值.
12.已知:一次函数y=kx+b的图象经过M(0,2),
N(1,3) 两点.(1)求k,b的值;
∴一次函数的解析式为:
y=x+2
(2)∵k=1,b=2
把y=0,x=a,代入y=x+2,得
a+2=0,
∴a= -2.
∴
函数点A(1,3) ,
解:
1.已知正比例函数y=kx(k≠0) 的图象经过点(-2,1),则这个正比例函数的解析式为( ).
A.y=2x B.y=-2x
C.y= x D.y=- x
1
2
1
2
D
练习巩固
2.P1(x1,y1),P2(x2,y2)是正比例函数y=-x图象上的两点,下列判断中,正确的是( ).
A.y1>y2 B.y1<y2
C.当x1<x2时,y1<y2 D.当x1<x2时,y1>y2
D
3.如果一个正比例函数的图象经过不同象限的两点A(2,m),B(n,3),那么一定有( )
A.m>0,n>0 B.m>0,n<0
C.m<0,n>0 D.m<0,n<0
D
4.下列函数中,y随x的增大而减小的函数是( )
A.y=2x+8 B.y=-2+4x
C.y=-2x+8 D.y=4x
C
6.一次函数y=mx+|m-1|的图象过点(0,2),且y随x的增大而增大,则m的值为( ).
A.-1 B.3 C.1 D.-1或3
B
5.若一次函数 y=(k-3)x+5,且y随x的增大而减小,则k的取值范围是( ).
A.k>0
B. k<0
C.k>3
D.k<3
C
7.把直线y=2x+3向上平移4个单位,所得
直线是函数__________的图象.
y=2x+7
8.把直线y=-2x-2向下移2个单位,
所得直线是函数__________的图象.
y=-2x-4
9.函数y=-2x-3在y轴上的截距是____.
-3
10.函数y=- x + 在y轴上的截距是____.
3
2
4
3
4
3
11.已知直线y=kx+b与直线y=2x平行,且
在y轴上的截距为-5,则此直线的解析
式为 .
y=2x-5
12.若一条直线经过点 (-1 ,1)和点 (1, 5 ),则这条直线与 x轴的交点坐标是 .
(- ,0)
3
2
-k+b=1
k+b=5
k=2
b=3
y=kx+b
y=2x+3
0=2x+3
(2)若一次函数y=kx+b的图象与x轴的交点
为A(a,0),求a的值.
13.已知:一次函数y=kx+b的图象经过M(0,2),
N(1,3) 两点.(1)求k,b的值;
∴一次函数的解析式为:
y=x+2
(2)∵k=1,b=2
把y=0,x=a,代入y=x+2,得
a+2=0,
∴a= -2.
∴
∴
∵一次函数y=kx+b过(0,2),(1,3)点,
解:(1)
b=2
k+b=3
k=1
b=2
(1)什么叫一次函数?正比例函数与一次函数有什么关系?我们主要研究了一次函数的哪些性质?
(2)我们是怎样研究一次函数性质的?
课堂小结
今天作业
课本P48页第9题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
