第12章 一次函数小结(4)实际问题与一次函数 课件(共21张PPT)
文档属性
| 名称 | 第12章 一次函数小结(4)实际问题与一次函数 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 926.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 22:18:02 | ||
图片预览







文档简介
(共21张PPT)
沪科版 八年级上册
第12章 一次函数小结(4)
实际问题与一次函数
教学目标:
1.能整理本章学习内容,建立相关知识之间的联系,优化知识结构;
2.会用一次函数模型描述和研究实际问题中的运动 变化规律;
3.进一步体会函数模型思想、数形结合思想及变化 和对应的思想.
课件说明
用一次函数解决实际问题
1.分段函数问题(分段价格、几何动点)由
形求式 (单个函数图象、多个函数图象)
2.方案设计问题(物资调运、方案比较).
3.一次函数最值问题.
知识要点
一次函数y=kx+b(k≠0)本来没有最大值,也没有最小值,但是由于在实际问题中,所列函数表达式中的自变量的取值往往有一定的限制,故有最大值或最小值.
(一)一次函数y=kx+b(k≠0)的最值
当k 时,y随x的增大而增大,
当k 时,y随x的增大而减小。
>0
<0
例1.A城有肥料200t,B城有肥料300t,现要把这些肥料全部运往C,D两乡.从A城运往C,D两乡运肥料的费用分别为20元/t和25元/t;从B城运往C,D两乡运肥料的费用分别是15元/t和24元/t.现C乡需要肥料240t,D乡需要肥料260t,怎样调运可是总运费最少?
典型例析
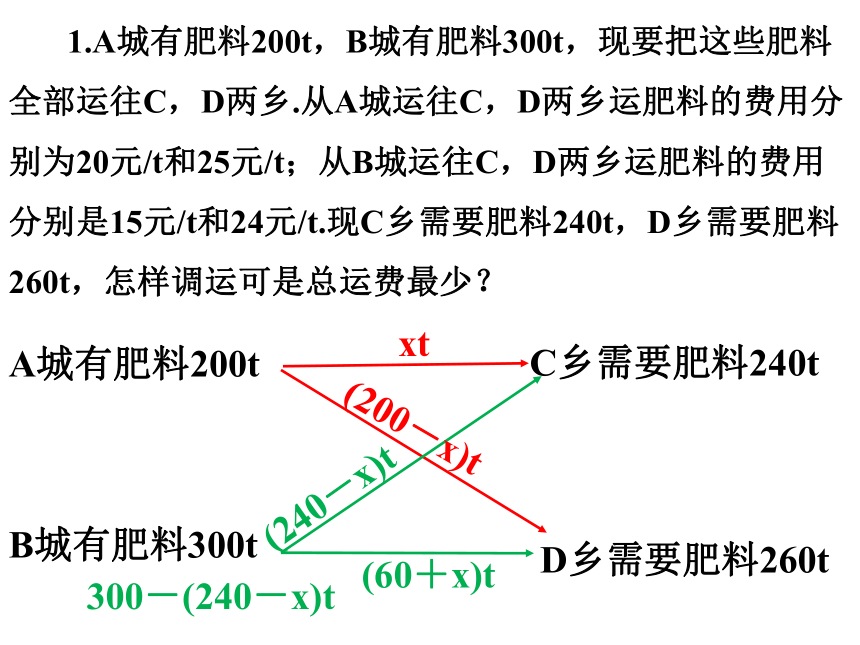
1.A城有肥料200t,B城有肥料300t,现要把这些肥料
全部运往C,D两乡.从A城运往C,D两乡运肥料的费用分
别为20元/t和25元/t;从B城运往C,D两乡运肥料的费用
分别是15元/t和24元/t.现C乡需要肥料240t,D乡需要肥料
260t,怎样调运可是总运费最少?
A城有肥料200t
B城有肥料300t
C乡需要肥料240t
D乡需要肥料260t
xt
(200-x)t
(60+x)t
(240-x)t
300-(240-x)t
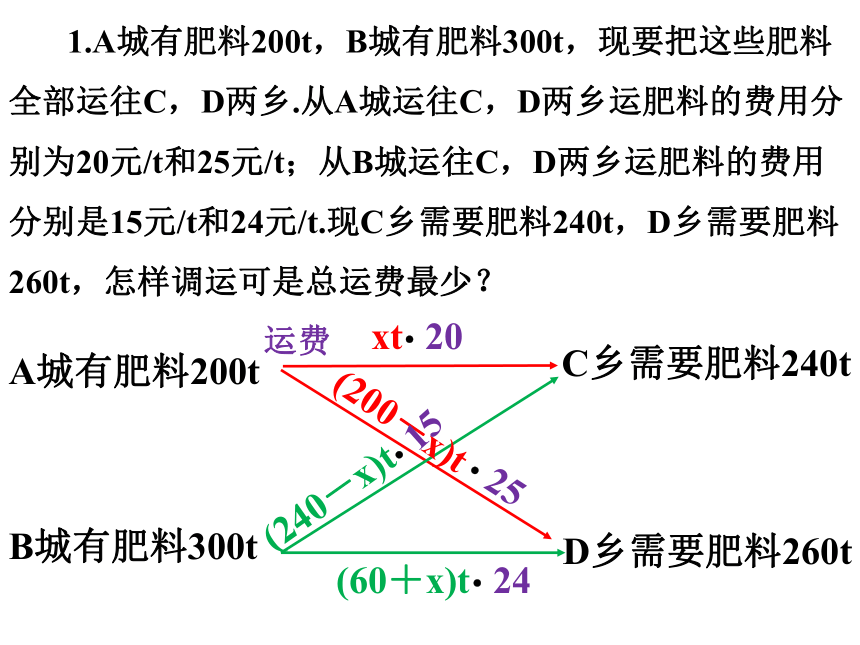
1.A城有肥料200t,B城有肥料300t,现要把这些肥料
全部运往C,D两乡.从A城运往C,D两乡运肥料的费用分
别为20元/t和25元/t;从B城运往C,D两乡运肥料的费用
分别是15元/t和24元/t.现C乡需要肥料240t,D乡需要肥料
260t,怎样调运可是总运费最少?
A城有肥料200t
B城有肥料300t
C乡需要肥料240t
xt
(200-x)t
(60+x)t
(240-x)t
20
●
25
●
24
●
15
●
运费
D乡需要肥料260t
A城有肥料200t
B城有肥料300t
C乡需要肥料240t
D乡需要肥料260t
xt
(200-x)t
(60+x)t
(240-x)t
20
●
25
●
24
●
15
●
20x
+25(200-x)
+15(240-x)
+24(60+x)
解:设从A城运肥料xt到C乡,总运费为y元,则有
y=
整理,得
y=
4x
+10040
(0≤x≤200)
∵k=4>0,
∴y随x的增大而增大,
∴x最小时y最小.
∵x最小值为0,
∴从A城运到C乡肥料为0t.
20x
+25(200-x)
+15(240-x)
+24(60+x)
解:设从A城运肥料xt到C乡,总运费为y元,则有
y=
整理,得
y=
4x
+10040
∵k=4>0,
∴y随x的增大而增大,
(0≤x≤200)
∴x最小时y最小.
∵x最小值为0,
∴从A城运到C乡肥料为0t.
即A城200t肥料全运往D乡,
再从B城的运60t肥料往D乡,
C乡所需要的240t肥料全从B城运,
可使总运费最少.
例2.在某火车站托运物品时,不超过1kg的物品需付2元,以后每增加1kg(不足1kg按1kg计)需增加托运费0.5元.设托运为pkg(p为整数)物品的费用为c.试写出c的计算公式.
解:c的计算公式为:
即:
c=0.5(p-1)+2
c=2
c=0.5p+1.5
c=2
(0<p≤1),
(p>1).
(0<p≤1),
(p>1).
2.在某火车站托运物品时,不超过1kg的物品需付2元,以后每增加1kg(不足1kg按1kg计)需增加托运费0.5元.设托运为pkg(p为整数)物品的费用为c.试写出c的计算公式.
c=0.5p+1.5
c=2
(0<p≤1),
(p>1).
O
p/kg
c/元
1
3
3
2
1
2
1.我市某商场有甲、乙两种商品,甲种每件进价15元,售价20元;乙种每件进价35元,售价45元.
(1)若商家同时购进甲、乙两种商品100件,设甲商品购进x件,售完此两种商品总利润为y元.写出y与x的函数关系式.
(2)该商家计划最多投入3 000元用于购进此两种商品共100件,则至少要购进多少件甲种商品?若售完这些商品,商家可获得的最大利润是多少元?
练习巩固
解:(1)设甲商品购进x件,则乙商品购进(100-x)件,
由题意,得
y=
∴y与x之间的函数关系式为:
1.我市某商场有甲、乙两种商品,甲种每件进价15元,售价20元;乙种每件进价35元,售价45元.
(1)若商家同时购进甲、乙两种商品100件,设甲商品购进x件,售完此两种商品总利润为y元.写出y与x的函数关系式.
y=-5x+1 000.
(20-15)x
+(45-35)(100-x)
=-5x+1 000,
(2)由题意,得
解得 x≥25.
∵y=-5x+1 000,k=-5<0,
∴y随x的增大而减小,
∴当x取最小值25时,y取最大值,
此时y=-5×25+1 000=875(元),
∴至少要购进25件甲种商品;
若售完这些商品,商家可获得的最大利润是875 元.
15x+35(100-x)≤3 000,
(1) 当 0≤x≤4时,
求y关于x的函数解析式;
(2) 当4<x≤12时,
求y关于x的函数解析式;
(3)每分进水、出水各多少升?
2.一个有进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水有出水,每分的进水量和出水量是两个常数.容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.
O
x
y
4
12
30
20
10
8
(1) 当 0≤x≤4时,求y关于x的函数解析式;
O
x/min
y/L
4
12
30
20
10
8
解:(1)
设所求的函数的解析式为
y=kx
∵函数的图象经过点(0,0)与(4,20),
y=5x
∴ 0≤x≤4时,y关于x的函数解析式为
∴20=4k
∴k=5
(2) 当 4<x≤12时,求y关于x的函数解析式;
O
x/min
y/L
4
12
30
20
10
8
解:(2)
设所求的函数的解析式为
∵函数的图象经过点(4,20)与(12,30),
∴ 4<x≤12时,y关于x的函数解析式为
∴
∴
y=kx+b
y= x+15
4k+b=20
12k+b=30
k =
b =
15
5
4
5
4
(3) 每分进水、出水各多少升?
2.一个有进水管与出水管的容器,从某时刻开始
4min内只进水不出水,在随后的8min内既进水有出水,
每分的进水量和出水量是两个常数.容器内的水量y(单位:
L)与时间x(单位:min)之间的关系如图所示.
O
x
y
4
12
30
20
10
8
(3)设每分的进水量为xL,出水量为yL,
4x=20
12x-8y=30
x =
y =
5
3.75
∴
∴
每分的进水量为5L,出水量为3.75L.
今天作业
课本P62页第12题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 八年级上册
第12章 一次函数小结(4)
实际问题与一次函数
教学目标:
1.能整理本章学习内容,建立相关知识之间的联系,优化知识结构;
2.会用一次函数模型描述和研究实际问题中的运动 变化规律;
3.进一步体会函数模型思想、数形结合思想及变化 和对应的思想.
课件说明
用一次函数解决实际问题
1.分段函数问题(分段价格、几何动点)由
形求式 (单个函数图象、多个函数图象)
2.方案设计问题(物资调运、方案比较).
3.一次函数最值问题.
知识要点
一次函数y=kx+b(k≠0)本来没有最大值,也没有最小值,但是由于在实际问题中,所列函数表达式中的自变量的取值往往有一定的限制,故有最大值或最小值.
(一)一次函数y=kx+b(k≠0)的最值
当k 时,y随x的增大而增大,
当k 时,y随x的增大而减小。
>0
<0
例1.A城有肥料200t,B城有肥料300t,现要把这些肥料全部运往C,D两乡.从A城运往C,D两乡运肥料的费用分别为20元/t和25元/t;从B城运往C,D两乡运肥料的费用分别是15元/t和24元/t.现C乡需要肥料240t,D乡需要肥料260t,怎样调运可是总运费最少?
典型例析
1.A城有肥料200t,B城有肥料300t,现要把这些肥料
全部运往C,D两乡.从A城运往C,D两乡运肥料的费用分
别为20元/t和25元/t;从B城运往C,D两乡运肥料的费用
分别是15元/t和24元/t.现C乡需要肥料240t,D乡需要肥料
260t,怎样调运可是总运费最少?
A城有肥料200t
B城有肥料300t
C乡需要肥料240t
D乡需要肥料260t
xt
(200-x)t
(60+x)t
(240-x)t
300-(240-x)t
1.A城有肥料200t,B城有肥料300t,现要把这些肥料
全部运往C,D两乡.从A城运往C,D两乡运肥料的费用分
别为20元/t和25元/t;从B城运往C,D两乡运肥料的费用
分别是15元/t和24元/t.现C乡需要肥料240t,D乡需要肥料
260t,怎样调运可是总运费最少?
A城有肥料200t
B城有肥料300t
C乡需要肥料240t
xt
(200-x)t
(60+x)t
(240-x)t
20
●
25
●
24
●
15
●
运费
D乡需要肥料260t
A城有肥料200t
B城有肥料300t
C乡需要肥料240t
D乡需要肥料260t
xt
(200-x)t
(60+x)t
(240-x)t
20
●
25
●
24
●
15
●
20x
+25(200-x)
+15(240-x)
+24(60+x)
解:设从A城运肥料xt到C乡,总运费为y元,则有
y=
整理,得
y=
4x
+10040
(0≤x≤200)
∵k=4>0,
∴y随x的增大而增大,
∴x最小时y最小.
∵x最小值为0,
∴从A城运到C乡肥料为0t.
20x
+25(200-x)
+15(240-x)
+24(60+x)
解:设从A城运肥料xt到C乡,总运费为y元,则有
y=
整理,得
y=
4x
+10040
∵k=4>0,
∴y随x的增大而增大,
(0≤x≤200)
∴x最小时y最小.
∵x最小值为0,
∴从A城运到C乡肥料为0t.
即A城200t肥料全运往D乡,
再从B城的运60t肥料往D乡,
C乡所需要的240t肥料全从B城运,
可使总运费最少.
例2.在某火车站托运物品时,不超过1kg的物品需付2元,以后每增加1kg(不足1kg按1kg计)需增加托运费0.5元.设托运为pkg(p为整数)物品的费用为c.试写出c的计算公式.
解:c的计算公式为:
即:
c=0.5(p-1)+2
c=2
c=0.5p+1.5
c=2
(0<p≤1),
(p>1).
(0<p≤1),
(p>1).
2.在某火车站托运物品时,不超过1kg的物品需付2元,以后每增加1kg(不足1kg按1kg计)需增加托运费0.5元.设托运为pkg(p为整数)物品的费用为c.试写出c的计算公式.
c=0.5p+1.5
c=2
(0<p≤1),
(p>1).
O
p/kg
c/元
1
3
3
2
1
2
1.我市某商场有甲、乙两种商品,甲种每件进价15元,售价20元;乙种每件进价35元,售价45元.
(1)若商家同时购进甲、乙两种商品100件,设甲商品购进x件,售完此两种商品总利润为y元.写出y与x的函数关系式.
(2)该商家计划最多投入3 000元用于购进此两种商品共100件,则至少要购进多少件甲种商品?若售完这些商品,商家可获得的最大利润是多少元?
练习巩固
解:(1)设甲商品购进x件,则乙商品购进(100-x)件,
由题意,得
y=
∴y与x之间的函数关系式为:
1.我市某商场有甲、乙两种商品,甲种每件进价15元,售价20元;乙种每件进价35元,售价45元.
(1)若商家同时购进甲、乙两种商品100件,设甲商品购进x件,售完此两种商品总利润为y元.写出y与x的函数关系式.
y=-5x+1 000.
(20-15)x
+(45-35)(100-x)
=-5x+1 000,
(2)由题意,得
解得 x≥25.
∵y=-5x+1 000,k=-5<0,
∴y随x的增大而减小,
∴当x取最小值25时,y取最大值,
此时y=-5×25+1 000=875(元),
∴至少要购进25件甲种商品;
若售完这些商品,商家可获得的最大利润是875 元.
15x+35(100-x)≤3 000,
(1) 当 0≤x≤4时,
求y关于x的函数解析式;
(2) 当4<x≤12时,
求y关于x的函数解析式;
(3)每分进水、出水各多少升?
2.一个有进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水有出水,每分的进水量和出水量是两个常数.容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.
O
x
y
4
12
30
20
10
8
(1) 当 0≤x≤4时,求y关于x的函数解析式;
O
x/min
y/L
4
12
30
20
10
8
解:(1)
设所求的函数的解析式为
y=kx
∵函数的图象经过点(0,0)与(4,20),
y=5x
∴ 0≤x≤4时,y关于x的函数解析式为
∴20=4k
∴k=5
(2) 当 4<x≤12时,求y关于x的函数解析式;
O
x/min
y/L
4
12
30
20
10
8
解:(2)
设所求的函数的解析式为
∵函数的图象经过点(4,20)与(12,30),
∴ 4<x≤12时,y关于x的函数解析式为
∴
∴
y=kx+b
y= x+15
4k+b=20
12k+b=30
k =
b =
15
5
4
5
4
(3) 每分进水、出水各多少升?
2.一个有进水管与出水管的容器,从某时刻开始
4min内只进水不出水,在随后的8min内既进水有出水,
每分的进水量和出水量是两个常数.容器内的水量y(单位:
L)与时间x(单位:min)之间的关系如图所示.
O
x
y
4
12
30
20
10
8
(3)设每分的进水量为xL,出水量为yL,
4x=20
12x-8y=30
x =
y =
5
3.75
∴
∴
每分的进水量为5L,出水量为3.75L.
今天作业
课本P62页第12题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
