第1章 有理数 小结(2)有理数相关的运算 课件(共26张PPT)
文档属性
| 名称 | 第1章 有理数 小结(2)有理数相关的运算 课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 00:00:00 | ||
图片预览



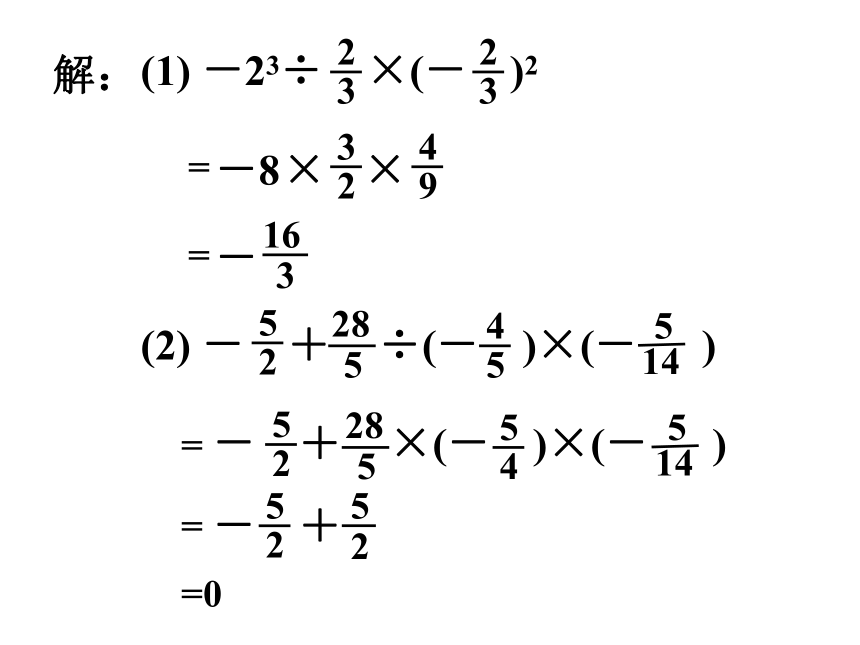
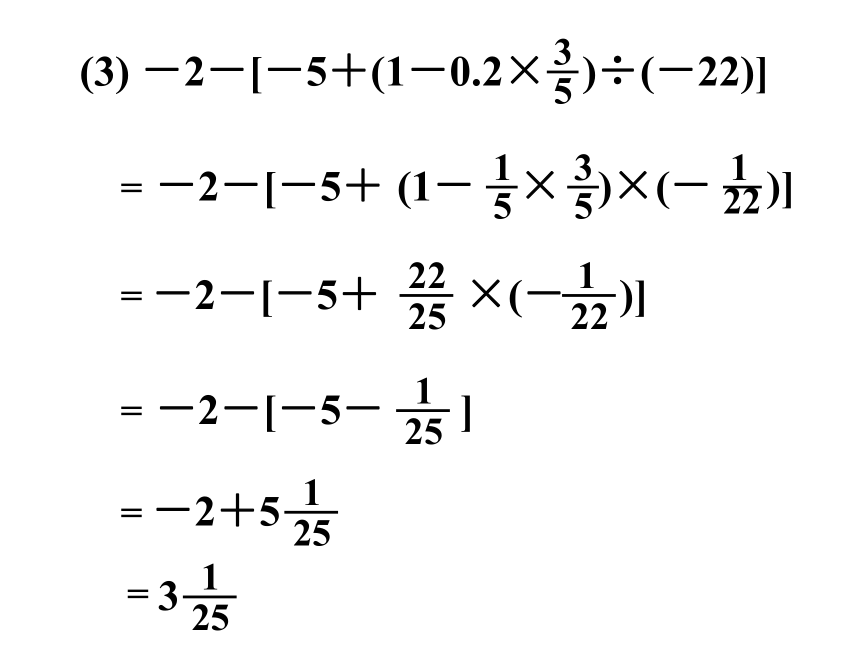



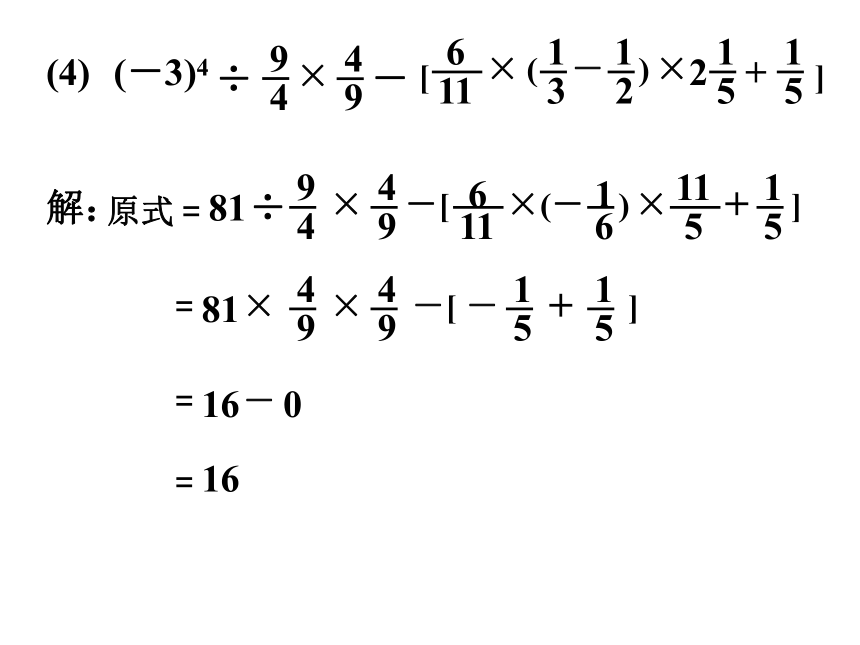
文档简介
(共26张PPT)
沪科版 七年级上册
第一章:有理数 小结(2)
有理数的相关运算
(1)先乘方,再乘除,最后加减;
(2)同级运算,从左到右进行;
(3)如有括号,先做括号内的运算,
按小括号、中括号、大括号依次进行.
有理数混合运算顺序的规定:
有理数运算有加法、减法、乘法、除法和乘方.
知识要点
典型例析
计算下列各题:
(1) -23÷ ×(- )2
2
3
2
3
(2) - + ÷(- )×(- )
5
14
5
2
28
5
4
5
(3) -2-[-5+(1-0.2× )÷(-22)]
3
5
有理数混合运算
解:
(1) -23÷ ×(- )2
2
3
2
3
=
-8
×
3
2
×
4
9
=
-
16
3
(2) - + ÷(- )×(- )
5
14
5
2
28
5
4
5
=
- + ×(- )×(- )
5
14
5
2
28
5
5
4
=
- +
5
2
5
2
=0
(3) -2-[-5+(1-0.2× )÷(-22)]
3
5
=
-2-[-5+ (1- × )×(- )]
3
5
1
5
1
22
=
-2-[-5+ ×(- )]
22
25
1
22
=
-2-[-5- ]
1
25
=
-2+5
1
25
=
3
1
25
=
(- )
1
6
×
4
5
×
10
=
-
4
3
解:
原式
(1) ( - ) ÷1 ÷
1
4
1
3
1
2
1
10
计算:
练习巩固
有理数混合运算
解:
原式
=
(-4)
×
(- )
5
7
×
(- )
7
4
-
1
8
=
-
5
-
1
8
=
-5
1
8
(2)
(-4)×(- )÷(- )- ( )3
1
2
5
7
4
7
(算小括号)
(再算括号里的乘方)
(算括号里的乘除)
(算括号里的加减)
原式=
-
2
3
×
[
1
3
+
( )2
1
12
÷
1
144
]
=
-
2
3
×
[
1
3
+
1
144
÷
1
144
]
=
-
2
3
×
[
1
3
+
1
]
=
-
2
3
×
4
3
=
-
8
9
(3)
- ×[ + ( - )2÷ ]
1
4
1
3
1
3
2
3
1
144
解:
原式
=
=
81
÷
9
4
×
4
9
-
[
6
11
×
(- )
1
6
×
11
5
+
1
5
]
81
×
4
9
×
4
9
-
[
-
1
5
+
1
5
]
=
16
-
0
=
16
[
×
(4)
(-3)4
÷
9
4
4
9
-
6
11
×
( - )
1
3
1
2
×
2
1
5
+
1
5
]
典型例析
运算律在有理数运算中的应用
(1) 21-49.5+10.2-2-3.5+19
计算下列各题:
(2) ( )2÷(-2 )+(11 +2 -13 )×24-(-5)3
1
4
1
2
1
4
1
3
3
4
(3) (-3)×(- )+0.25×24.5+(-5 )×(-25%)
1
4
1
2
解:
(1) 21-49.5+10.2-2-3.5+19
=
[(21+19)+10.2 ]+ [(-49.5-3.5)-2]
=
50.2+ (-55)
=
-4.8
(2) ( )2÷(-2 )+(11 +2 - 8 )×24-(-5)3
1
4
1
2
1
4
1
3
5
6
=
1
16
×(- )
2
5
+( + - )×24
45
4
7
3
53
6
-(-125)
=
-
40
1
+270 +56 -212
+125
=
238
39
40
(3) (-3)×(- )+0.25×24.5+(-5 )×(-25%)
1
4
1
2
=
3×
1
4
=
×
1
4
=
33
4
+ ×24
1
4
1
2
+5 ×
1
2
1
4
(3+24 +5 )
1
2
1
2
有理数运算技巧总结:
(1)运用运算律将正负数分别相加.
(2)分母相同或有倍数关系的分数结合相加.
(3)在式子中若既有分数又有小数,把小数统一
成分数或把分数统一成小数.
(4)互为相反数的两数可先相加.
(5)带分数整数部分,小数部分可拆开相加.
典型例析
倒数计算法
对于a÷(b+c+d+e)形式的计算,常先求
(b+c+d+e)÷a的值,再取倒数.
计算:(- )÷( - + - )
2
3
1
6
3
4
24
1
12
5
解:因为 ( - + - ) ÷
2
3
1
6
3
4
24
1
12
5
(- )
=
( - + - ) ×
2
3
1
6
3
4
12
5
(-24 )
=
-16+10-4 +18
=8
所以:(- )÷( - + - )
2
3
1
6
3
4
24
1
12
5
=
1
8
(1)
-43
×
22
-
(-4)3
×
(-2)2
(2)
-5
×
32
-
(-5 )2
×3
(3)
(-1)1
+
(-1)2
+
(-1)3
+
+
(-1)100
…
(- )
(4)
7
8
÷
( - )
7
4
7
8
-
7
12
练习巩固
(1)
-43
×
22
-
(-4)3
×
(-2)2
(2)
-5
×
32
-
(-5 )2
×3
练习巩固
解:
=
-43
×
22
-
(-4)3
×
22
=
[
-43
×
22
-
(-4)3
]
=
22
×0
=0
=
-5
×
9
-
152
=
-45
-
225
= -270
(3)
(-1)1
+
(-1)2
+
(-1)3
+
+
(-1)100
…
(- )
(4)
7
8
÷
( - )
7
4
7
8
-
7
12
=
=0
[(-1)
+
1]
+
[(-1)
+1]
+
[(-1) +1]
+ …
(- )
7
8
÷
( - )
7
4
7
8
-
7
12
=
解:因为
(- )
8
7
×
( - )
7
4
7
8
-
7
12
=
-2+1 +
2
3
= -
1
3
(- )
所以
7
8
÷
( - )
7
4
7
8
-
7
12
= -3
1.有10筐荔枝,以每筐25千克为标准,超过的千克数记作正数,不足的千克数记作负数,称重的结果记录如下(单位:千克):
+ 0.6,-1.4,-1.5, -0.3, + 0.4,
+ 0.3,+ 0.5,-1.2, + 0.8, + 0.7.
请通过计算回答下列问题:
(1)实际称得的总重量与标准总重量相比,超过或不足多少千克?
(2)这10筐荔枝的实际总重量是多少千克?
典型例析
有理数的应用
答:(1)实际重量也标准重量相比,不足1.1千克;
(2)这10筐荔枝的实际总重量是248.9千克.
解:(1)根据题意:有
(+0.6)+(-1.4)+(-1.5)+(-0.3) +(+ 0.4)
+(+0.3) +(+0.5)+(-1.2)+(+0.8)+(+0.7)
=-1.1(千克)
所以实际重量也标准重量相比,不足1.1千克.
(2)实际总重量:
25×10+(-1.1)=250-1.1
所以这10筐荔枝的实际总重量是198.9千克.
=248.9(千克)
典型例析
有理数的应用
2.若︱x - ︱+(2y+1)2=0,求x2 +y3的值.
1
2
解:
(2y+1)2=0,
2y+1=0,
所以 x= ,
y= -
因为︱x - ︱+(2y+1)2=0,
1
2
所以︱x - ︱=0,
1
2
所以 x- =0,
1
2
1
2
1
2
所以x2 +y3
= ( )2+(- )3
1
2
1
2
= -
1
4
1
8
=
1
8
典型例析
有理数的应用
如图,数轴上标出了9个点,相邻两个点之间的距离都相等已知点A表示- 6,点H表示8.
(1)点B表示的有理数是 ,表示原点的点是 ;
(2)若图中数轴上另有点M到点A,点H的距离之
和为15,则这样的点M表示的有理数是 .
-6
A
B
C
D
E
F
G
H
8
-4
D
-6.5
或8.5
小虫从某点O出发在一直线上来回爬行,假定向右爬行的路程记为正,向左爬行的路程记为负,爬过的路程依次为(单位:cm):
.
问:(1)小虫是否回到原点O ?
(2)小虫离开出发点O最远是多少cm?
(3)在爬行过程中,如果每爬行1 cm奖励一粒芝麻,则小虫共可得到多少粒芝麻?
练习巩固
.
+ 5,-3, +10, -8, - 6,+12, -10.
解:(1)根据题意:有
(+5)+(-3)+(+10)+(-8) +(-6)+(+12)+(-10)
=(5 +10 +12)+(-3-8-6-10)
所以小虫是回到了原点O.
(2) 小虫离开出发点O最远是12cm.
=27+(-27)
=0
(3)因为小虫每爬行1 cm奖励一粒芝麻,
=54(cm)
所以小虫共可得到54粒芝麻.
小虫共爬行了27+︱-27︱
今天作业
课本P53第8题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 七年级上册
第一章:有理数 小结(2)
有理数的相关运算
(1)先乘方,再乘除,最后加减;
(2)同级运算,从左到右进行;
(3)如有括号,先做括号内的运算,
按小括号、中括号、大括号依次进行.
有理数混合运算顺序的规定:
有理数运算有加法、减法、乘法、除法和乘方.
知识要点
典型例析
计算下列各题:
(1) -23÷ ×(- )2
2
3
2
3
(2) - + ÷(- )×(- )
5
14
5
2
28
5
4
5
(3) -2-[-5+(1-0.2× )÷(-22)]
3
5
有理数混合运算
解:
(1) -23÷ ×(- )2
2
3
2
3
=
-8
×
3
2
×
4
9
=
-
16
3
(2) - + ÷(- )×(- )
5
14
5
2
28
5
4
5
=
- + ×(- )×(- )
5
14
5
2
28
5
5
4
=
- +
5
2
5
2
=0
(3) -2-[-5+(1-0.2× )÷(-22)]
3
5
=
-2-[-5+ (1- × )×(- )]
3
5
1
5
1
22
=
-2-[-5+ ×(- )]
22
25
1
22
=
-2-[-5- ]
1
25
=
-2+5
1
25
=
3
1
25
=
(- )
1
6
×
4
5
×
10
=
-
4
3
解:
原式
(1) ( - ) ÷1 ÷
1
4
1
3
1
2
1
10
计算:
练习巩固
有理数混合运算
解:
原式
=
(-4)
×
(- )
5
7
×
(- )
7
4
-
1
8
=
-
5
-
1
8
=
-5
1
8
(2)
(-4)×(- )÷(- )- ( )3
1
2
5
7
4
7
(算小括号)
(再算括号里的乘方)
(算括号里的乘除)
(算括号里的加减)
原式=
-
2
3
×
[
1
3
+
( )2
1
12
÷
1
144
]
=
-
2
3
×
[
1
3
+
1
144
÷
1
144
]
=
-
2
3
×
[
1
3
+
1
]
=
-
2
3
×
4
3
=
-
8
9
(3)
- ×[ + ( - )2÷ ]
1
4
1
3
1
3
2
3
1
144
解:
原式
=
=
81
÷
9
4
×
4
9
-
[
6
11
×
(- )
1
6
×
11
5
+
1
5
]
81
×
4
9
×
4
9
-
[
-
1
5
+
1
5
]
=
16
-
0
=
16
[
×
(4)
(-3)4
÷
9
4
4
9
-
6
11
×
( - )
1
3
1
2
×
2
1
5
+
1
5
]
典型例析
运算律在有理数运算中的应用
(1) 21-49.5+10.2-2-3.5+19
计算下列各题:
(2) ( )2÷(-2 )+(11 +2 -13 )×24-(-5)3
1
4
1
2
1
4
1
3
3
4
(3) (-3)×(- )+0.25×24.5+(-5 )×(-25%)
1
4
1
2
解:
(1) 21-49.5+10.2-2-3.5+19
=
[(21+19)+10.2 ]+ [(-49.5-3.5)-2]
=
50.2+ (-55)
=
-4.8
(2) ( )2÷(-2 )+(11 +2 - 8 )×24-(-5)3
1
4
1
2
1
4
1
3
5
6
=
1
16
×(- )
2
5
+( + - )×24
45
4
7
3
53
6
-(-125)
=
-
40
1
+270 +56 -212
+125
=
238
39
40
(3) (-3)×(- )+0.25×24.5+(-5 )×(-25%)
1
4
1
2
=
3×
1
4
=
×
1
4
=
33
4
+ ×24
1
4
1
2
+5 ×
1
2
1
4
(3+24 +5 )
1
2
1
2
有理数运算技巧总结:
(1)运用运算律将正负数分别相加.
(2)分母相同或有倍数关系的分数结合相加.
(3)在式子中若既有分数又有小数,把小数统一
成分数或把分数统一成小数.
(4)互为相反数的两数可先相加.
(5)带分数整数部分,小数部分可拆开相加.
典型例析
倒数计算法
对于a÷(b+c+d+e)形式的计算,常先求
(b+c+d+e)÷a的值,再取倒数.
计算:(- )÷( - + - )
2
3
1
6
3
4
24
1
12
5
解:因为 ( - + - ) ÷
2
3
1
6
3
4
24
1
12
5
(- )
=
( - + - ) ×
2
3
1
6
3
4
12
5
(-24 )
=
-16+10-4 +18
=8
所以:(- )÷( - + - )
2
3
1
6
3
4
24
1
12
5
=
1
8
(1)
-43
×
22
-
(-4)3
×
(-2)2
(2)
-5
×
32
-
(-5 )2
×3
(3)
(-1)1
+
(-1)2
+
(-1)3
+
+
(-1)100
…
(- )
(4)
7
8
÷
( - )
7
4
7
8
-
7
12
练习巩固
(1)
-43
×
22
-
(-4)3
×
(-2)2
(2)
-5
×
32
-
(-5 )2
×3
练习巩固
解:
=
-43
×
22
-
(-4)3
×
22
=
[
-43
×
22
-
(-4)3
]
=
22
×0
=0
=
-5
×
9
-
152
=
-45
-
225
= -270
(3)
(-1)1
+
(-1)2
+
(-1)3
+
+
(-1)100
…
(- )
(4)
7
8
÷
( - )
7
4
7
8
-
7
12
=
=0
[(-1)
+
1]
+
[(-1)
+1]
+
[(-1) +1]
+ …
(- )
7
8
÷
( - )
7
4
7
8
-
7
12
=
解:因为
(- )
8
7
×
( - )
7
4
7
8
-
7
12
=
-2+1 +
2
3
= -
1
3
(- )
所以
7
8
÷
( - )
7
4
7
8
-
7
12
= -3
1.有10筐荔枝,以每筐25千克为标准,超过的千克数记作正数,不足的千克数记作负数,称重的结果记录如下(单位:千克):
+ 0.6,-1.4,-1.5, -0.3, + 0.4,
+ 0.3,+ 0.5,-1.2, + 0.8, + 0.7.
请通过计算回答下列问题:
(1)实际称得的总重量与标准总重量相比,超过或不足多少千克?
(2)这10筐荔枝的实际总重量是多少千克?
典型例析
有理数的应用
答:(1)实际重量也标准重量相比,不足1.1千克;
(2)这10筐荔枝的实际总重量是248.9千克.
解:(1)根据题意:有
(+0.6)+(-1.4)+(-1.5)+(-0.3) +(+ 0.4)
+(+0.3) +(+0.5)+(-1.2)+(+0.8)+(+0.7)
=-1.1(千克)
所以实际重量也标准重量相比,不足1.1千克.
(2)实际总重量:
25×10+(-1.1)=250-1.1
所以这10筐荔枝的实际总重量是198.9千克.
=248.9(千克)
典型例析
有理数的应用
2.若︱x - ︱+(2y+1)2=0,求x2 +y3的值.
1
2
解:
(2y+1)2=0,
2y+1=0,
所以 x= ,
y= -
因为︱x - ︱+(2y+1)2=0,
1
2
所以︱x - ︱=0,
1
2
所以 x- =0,
1
2
1
2
1
2
所以x2 +y3
= ( )2+(- )3
1
2
1
2
= -
1
4
1
8
=
1
8
典型例析
有理数的应用
如图,数轴上标出了9个点,相邻两个点之间的距离都相等已知点A表示- 6,点H表示8.
(1)点B表示的有理数是 ,表示原点的点是 ;
(2)若图中数轴上另有点M到点A,点H的距离之
和为15,则这样的点M表示的有理数是 .
-6
A
B
C
D
E
F
G
H
8
-4
D
-6.5
或8.5
小虫从某点O出发在一直线上来回爬行,假定向右爬行的路程记为正,向左爬行的路程记为负,爬过的路程依次为(单位:cm):
.
问:(1)小虫是否回到原点O ?
(2)小虫离开出发点O最远是多少cm?
(3)在爬行过程中,如果每爬行1 cm奖励一粒芝麻,则小虫共可得到多少粒芝麻?
练习巩固
.
+ 5,-3, +10, -8, - 6,+12, -10.
解:(1)根据题意:有
(+5)+(-3)+(+10)+(-8) +(-6)+(+12)+(-10)
=(5 +10 +12)+(-3-8-6-10)
所以小虫是回到了原点O.
(2) 小虫离开出发点O最远是12cm.
=27+(-27)
=0
(3)因为小虫每爬行1 cm奖励一粒芝麻,
=54(cm)
所以小虫共可得到54粒芝麻.
小虫共爬行了27+︱-27︱
今天作业
课本P53第8题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
