第1章 有理数 小结(1)有理数相关的概念 课件(共31张PPT)
文档属性
| 名称 | 第1章 有理数 小结(1)有理数相关的概念 课件(共31张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 00:00:00 | ||
图片预览








文档简介
(共31张PPT)
沪科版 七年级上册
第1章:有理数 小结(1)
有理数的相关概念
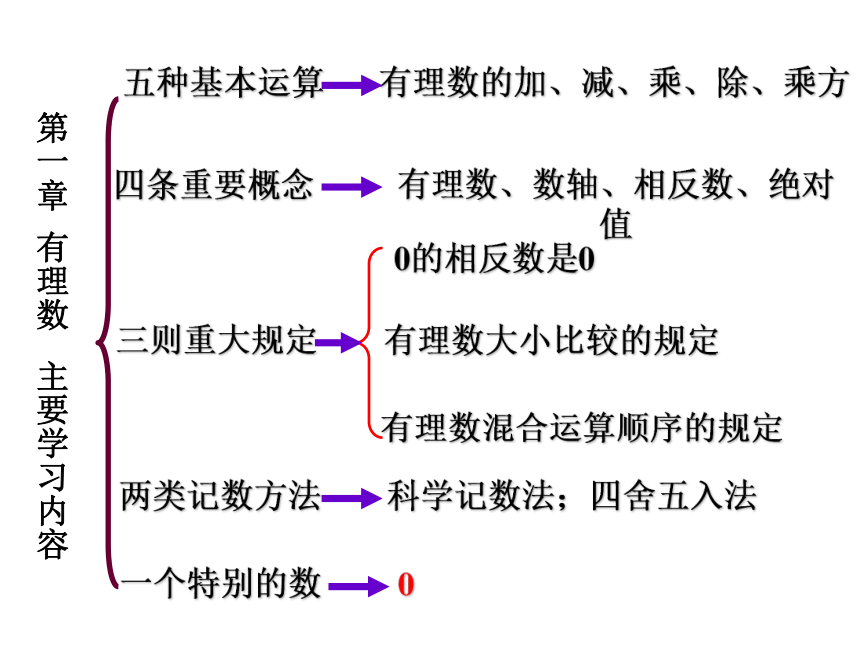
五种基本运算
三则重大规定
四条重要概念
两类记数方法
一个特别的数
有理数的加、减、乘、除、乘方
有理数、数轴、相反数、绝对值
科学记数法;四舍五入法
有理数大小比较的规定
有理数混合运算顺序的规定
0的相反数是0
第一章 有理数 主要学习内容
0
(1)同号两数相加,取相同符号,并把绝对值相加.
(2)绝对值不相等的异号两数相加,取绝对值较大的加
数的符号,并用较大的绝对值减去较小的绝对值。
互为相反数的两个数相加得0.
(3)一个数同0相加,仍得这个数.
1.有理数的加法法则:
减去一个数,等于加上这个数的相反数.
2.有理数减法法则:
一、五种基本运算
3.有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数同0相乘,都得0.
两数相除,同号得正,异号得负,并把绝对值相除.
0除以任何非0数都得0.
4.有理数除法法则:
除以一个不等于0的数,等于乘这个的数的倒数.
求相同因数的积的运算叫做乘方.
5.有理数乘方:
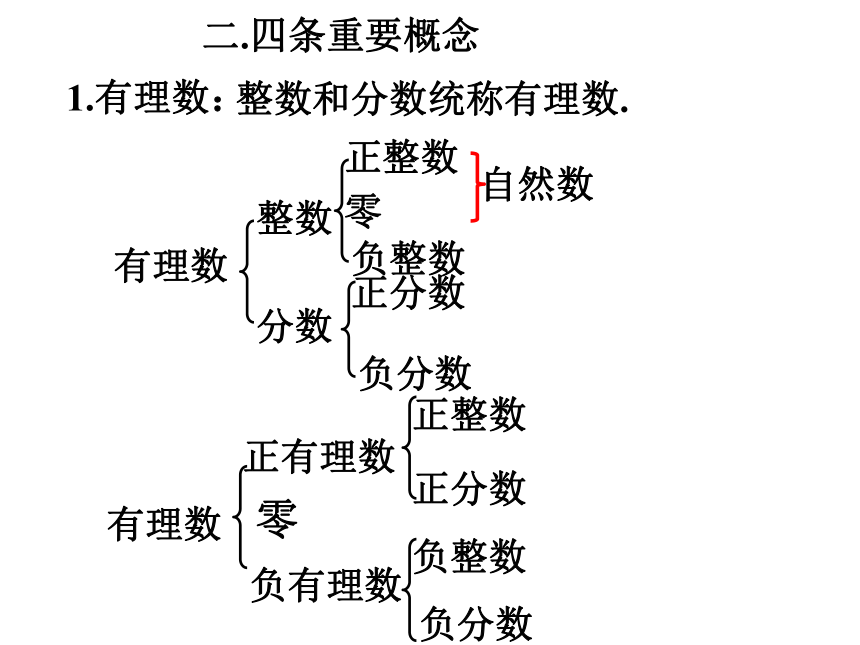
1.有理数:
整数和分数统称有理数.
有理数
整数
分数
正整数
负整数
正分数
负分数
有理数
正有理数
零
负有理数
正整数
正分数
负整数
负分数
自然数
零
二.四条重要概念
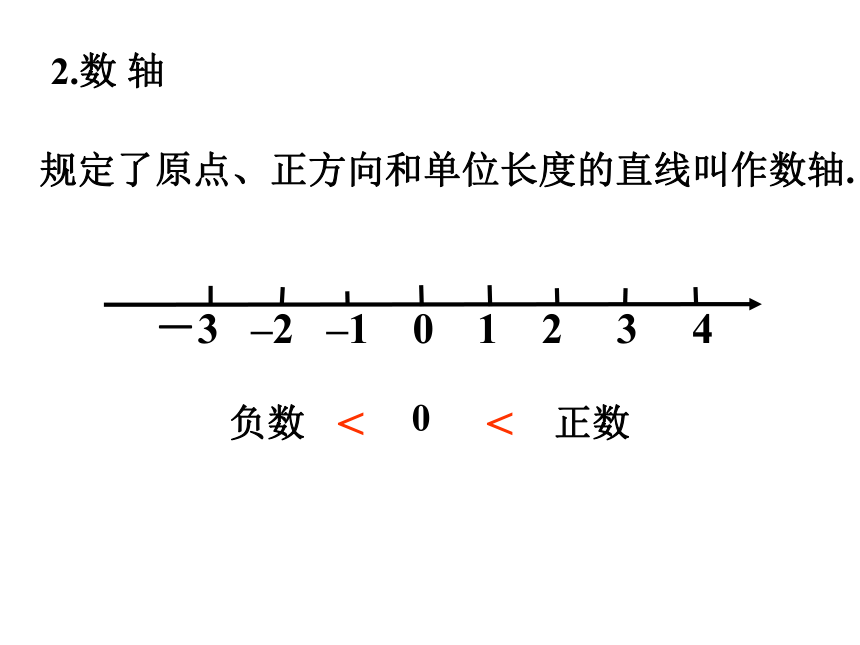
2.数 轴
规定了原点、正方向和单位长度的直线叫作数轴.
-3 –2 –1 0 1 2 3 4
0
负数
正数
<
<
只有符号不同的两个数,叫做互为相反数.
(1) 数a的相反数是-a.
(2) 0的相反数是0.
(3) 若a、b互为相反数,则a+b=0.
3.相反数
数a的绝对值就是数轴上表示数a的点与原点的距离.
1) 数a的绝对值记作︱a︱;
若a>0,则︱a︱= ;
2) 若a<0,则︱a︱= ;
若a =0,则︱a︱= ;
a
-a
0
3) 对任何有理数a,︱a︱一定是非负数.
4.绝对值
在数轴上表示有理数,它们从左到右的顺序,就是从小到大的顺序,即左边的数小于右边的数.
1.有理数大小的规定:
(1)正数大于0,0大于负数,正数大于负数;
(2) 两个负数,绝对值大的反而小.
三. 三则重大规定
(1)先乘方,再乘除,最后加减;
(2)同级运算,从左到右进行;
(3)如有括号,先做括号内的运算,
按小括号、中括号、大括号依次进行.
2.有理数混合运算顺序的规定:
1.科学记数法:
把一个数记成a×10n的形式,其中a是整数数位只有一位的数,这种记数法叫做科学记数法.
2.近似数:
与实际接近的数.
通常由四舍五入得到.
四.两类记数方法
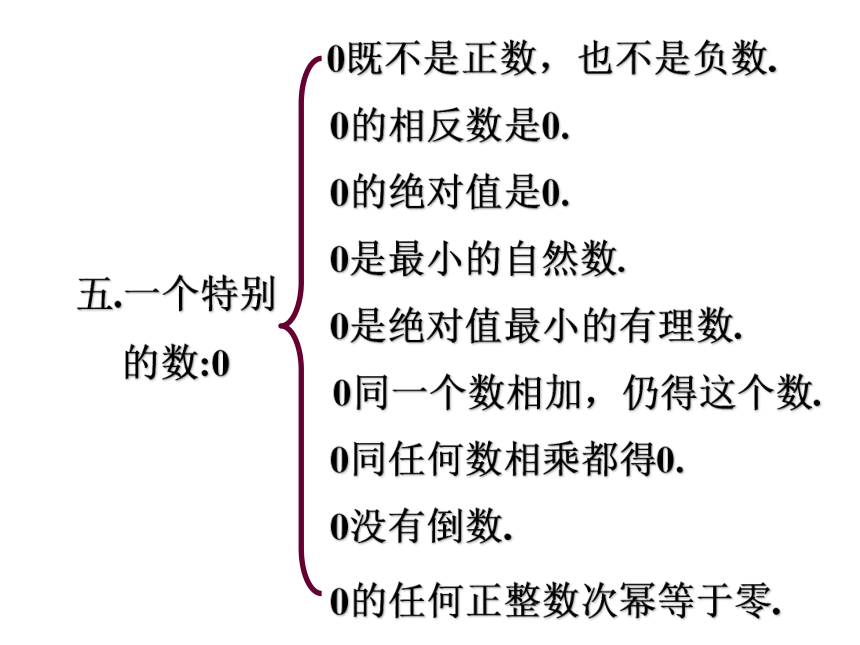
五.一个特别 的数:0
0既不是正数,也不是负数.
0的相反数是0.
0的绝对值是0.
0是绝对值最小的有理数.
0是最小的自然数.
0同一个数相加,仍得这个数.
0没有倒数.
0同任何数相乘都得0.
0的任何正整数次幂等于零.
典型例析
1.已知a,-b互为相反数,c,-d互为倒数,
|m| =3,求 -cd +m的值.
a-b
m
解:
因为a,-b互为相反数,
所以a-b=0.
因为c,-d互为倒数,
所以-cd=1.
因为|m| =3,
所以m=±3.
当m=3时,
-cd +m=
a-b
m
0
3
+1 +3
=4.
当m=-3时,
-cd +m=
a-b
m
0
-3
+1-3
=-2.
所以
-cd +m的值为
a-b
m
4或-2.
2.如果| a |=8,|b|=5,且a+b>0,求a-b的值.
解:
因为| a |=8,
所以a=8
或a=-8,
因为| b |=5,
所以b=5
或b=-5,
因为a+b>0,
所以a=8,
b=5
或b=-5,
所以a-b=
8-5
=3,
或a-b=
8-(-5)
=13.
典型例析
典型例析
3.已知| m |=m+2.求m2022 + 3m2023+2的值.
解:
当m>0时,
根据绝对值的意义,得
m =m+2,
所以0 =2,
所以m不可能大于0;
当m>0时,
根据绝对值的意义,得
0 =2,
所以m不可能等于0;
当m<0时,
根据绝对值的意义,得
-m =m+2,
所以m =-1.
所以m2022 + 3m2023+2
=(-1)2022 +3×(-1)2023+2
=0
①不带“-”号的数都是正数 ( )
⑤一个有理数不是正数就是负数 ( )
⑥0℃表示没有温度 ( )
③如果a是正数,那么-a一定是负数( )
④不存在既不是正数,也不是负数的数( )
②带“+”号的数都是正数 ( )
×
×
×
×
×
√
1)判断题:
1.有理数的分类
练习巩固
3)填空:
最小的自然数是 ,
最大的负整数是 ,
最小的正整数是 ,
最大的非正数是 .
2)判断:
(1)整数一定是自然数( )
(2)自然数一定是整数( )
×
√
0
-1
1
0
1.有理数的分类
4)把下列各数填在相应额大括号内:
-0.1,-789,25,0,-20,-3.14, ,5.3.
正有理数集 { …}
负有理数集{ …}
整数集{ …}
4
5
-0.1,
-789,
25,
-20,
-3.14,
5.3,
25,
0,
4
5
-789,
-20,
,
1.有理数的分类
2.与原点的距离为三个单位的点有__个,他们分别表
示的有理数是 和 .
+3
-3
2
3.与+3表示的点距离2000个单位的点有__个,他们
分别表示的有理数是__ __ 和 .
1.两个有理数表示较大的数的点离原点的距离较近( )
×
2
2003
-1997
4. +3表示的点与-2表示的点距离是__个单位。
5
2.数 轴
-0.5,-3.5, 2.5, ,-(-4).
0
1
2
3
-1
-2
-3
-4
4
| - |
3
2
●
●
●
●
●
-(-4)
-0.5
-3.5
2.5
| - |
3
2
| - |
3
2
-3.5
-0.5
2.5
-(-4)
>
>
>
>
画一条数轴,在数轴上标出下列各数,再将它们按由小到大的顺序用不等号连接起来.
4. 只要符号不同,这两个数就是相反数( )
2.互为相反数的两个数在数轴上位于原点两旁( )
1.一个数的相反数是最小的正整数,这个数是( )
A . -1 B. 1 C .±1 D. 0
A
×
×
3.位于原点两旁的数是互为相反数( )
5.表示相反意义的量的两个数互为相反数( )
×
×
6.若-a=-8,则-a的相反数是 ;
-(-4)的相反数是 .
8
-4
3.相反数
1)绝对值等于它本身的数是正数( )
5)任何数的绝对值都不是负数( )
2)绝对值等于它的相反数的数是负数( )
3)正数的绝对值大于负数的绝对值( )
4) 绝对值较大的数较大( )
×
×
×
×
√
4.绝对值
1)判断:
2)判断:
(1)|5|=|-5| ( )
(2)|-0.3|=|0.3| ( )
(3)|3|>0 ( )
(4)|-1.4|>0 ( )
(5)有理数的绝对值一定是正数 ( )
(6)若a=b,则|a|=|b| ( )
(7)若|a|=|b|,则a=b ( )
(8)若|a|=-a,则a必为负数 ( )
×
√
√
√
√
√
×
×
5.倒数
如果两个有理数数的乘积为1,我们称这两个有理数互为倒数.
(1) 的倒数是 ; -2的倒数是 .
① 和(-7);
②-1 和- ;
(2) 下列各组数中,互为倒数的有( ).
A.3组 B.4组 C.5组 D.6组
③-|-4|和- ;
④ 0和0
⑤1 和-1;
⑥3.2和 .
1
7
1
5
5
6
1
4
5
16
2
5
5
2
1
2
-
A
6.科学记数法
梧州市是世界最大的人工宝石加工集聚基地,年产量达约12 000 000 000粒,市场份额占全国产量的80%、世界产量的70%,被誉为“世界人工宝石之都”.请你将12 000 000 000用科学记数法表示为 ( )
A.12×109 B.1.2×1010
C.0.12×1011 D.120×108
B
7.近似数
下列说法正确的是( ).
A.0.720精确到百分位
B.3.6万精确到个位
C.5.078精确到千分位
D.8.66×106精确到百分位
C
8.已知a,b互为相反数,c,d互为倒数,
|m| =4,求 +cd +m的值.
a+b
m
解:
因为a,b互为相反数,
所以a+b=0.
因为c,d互为倒数,
所以cd=1.
因为|m| =4,
所以m=±4.
当m=4时,
+cd +m=
a+b
m
0
4
+1 +4
=5.
当m=-4时,
+ cd +m=
a+ b
m
0
-4
+1-4
=-3.
所以
+cd +m的值为
a+ b
m
5或-3.
9.如果| a |=8,|b|=5,且a+b<0,求a-b的值.
解:
因为| a |=8,
所以a=8
或a=-8,
因为| b |=5,
所以b=5
或b=-5,
因为a+b<0,
所以a= - 8,
b=5
或b=-5,
所以a-b=
- 8-5
= -13,
或a-b=
- 8-(-5)
= -3.
今天作业
课本P52第6题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 七年级上册
第1章:有理数 小结(1)
有理数的相关概念
五种基本运算
三则重大规定
四条重要概念
两类记数方法
一个特别的数
有理数的加、减、乘、除、乘方
有理数、数轴、相反数、绝对值
科学记数法;四舍五入法
有理数大小比较的规定
有理数混合运算顺序的规定
0的相反数是0
第一章 有理数 主要学习内容
0
(1)同号两数相加,取相同符号,并把绝对值相加.
(2)绝对值不相等的异号两数相加,取绝对值较大的加
数的符号,并用较大的绝对值减去较小的绝对值。
互为相反数的两个数相加得0.
(3)一个数同0相加,仍得这个数.
1.有理数的加法法则:
减去一个数,等于加上这个数的相反数.
2.有理数减法法则:
一、五种基本运算
3.有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数同0相乘,都得0.
两数相除,同号得正,异号得负,并把绝对值相除.
0除以任何非0数都得0.
4.有理数除法法则:
除以一个不等于0的数,等于乘这个的数的倒数.
求相同因数的积的运算叫做乘方.
5.有理数乘方:
1.有理数:
整数和分数统称有理数.
有理数
整数
分数
正整数
负整数
正分数
负分数
有理数
正有理数
零
负有理数
正整数
正分数
负整数
负分数
自然数
零
二.四条重要概念
2.数 轴
规定了原点、正方向和单位长度的直线叫作数轴.
-3 –2 –1 0 1 2 3 4
0
负数
正数
<
<
只有符号不同的两个数,叫做互为相反数.
(1) 数a的相反数是-a.
(2) 0的相反数是0.
(3) 若a、b互为相反数,则a+b=0.
3.相反数
数a的绝对值就是数轴上表示数a的点与原点的距离.
1) 数a的绝对值记作︱a︱;
若a>0,则︱a︱= ;
2) 若a<0,则︱a︱= ;
若a =0,则︱a︱= ;
a
-a
0
3) 对任何有理数a,︱a︱一定是非负数.
4.绝对值
在数轴上表示有理数,它们从左到右的顺序,就是从小到大的顺序,即左边的数小于右边的数.
1.有理数大小的规定:
(1)正数大于0,0大于负数,正数大于负数;
(2) 两个负数,绝对值大的反而小.
三. 三则重大规定
(1)先乘方,再乘除,最后加减;
(2)同级运算,从左到右进行;
(3)如有括号,先做括号内的运算,
按小括号、中括号、大括号依次进行.
2.有理数混合运算顺序的规定:
1.科学记数法:
把一个数记成a×10n的形式,其中a是整数数位只有一位的数,这种记数法叫做科学记数法.
2.近似数:
与实际接近的数.
通常由四舍五入得到.
四.两类记数方法
五.一个特别 的数:0
0既不是正数,也不是负数.
0的相反数是0.
0的绝对值是0.
0是绝对值最小的有理数.
0是最小的自然数.
0同一个数相加,仍得这个数.
0没有倒数.
0同任何数相乘都得0.
0的任何正整数次幂等于零.
典型例析
1.已知a,-b互为相反数,c,-d互为倒数,
|m| =3,求 -cd +m的值.
a-b
m
解:
因为a,-b互为相反数,
所以a-b=0.
因为c,-d互为倒数,
所以-cd=1.
因为|m| =3,
所以m=±3.
当m=3时,
-cd +m=
a-b
m
0
3
+1 +3
=4.
当m=-3时,
-cd +m=
a-b
m
0
-3
+1-3
=-2.
所以
-cd +m的值为
a-b
m
4或-2.
2.如果| a |=8,|b|=5,且a+b>0,求a-b的值.
解:
因为| a |=8,
所以a=8
或a=-8,
因为| b |=5,
所以b=5
或b=-5,
因为a+b>0,
所以a=8,
b=5
或b=-5,
所以a-b=
8-5
=3,
或a-b=
8-(-5)
=13.
典型例析
典型例析
3.已知| m |=m+2.求m2022 + 3m2023+2的值.
解:
当m>0时,
根据绝对值的意义,得
m =m+2,
所以0 =2,
所以m不可能大于0;
当m>0时,
根据绝对值的意义,得
0 =2,
所以m不可能等于0;
当m<0时,
根据绝对值的意义,得
-m =m+2,
所以m =-1.
所以m2022 + 3m2023+2
=(-1)2022 +3×(-1)2023+2
=0
①不带“-”号的数都是正数 ( )
⑤一个有理数不是正数就是负数 ( )
⑥0℃表示没有温度 ( )
③如果a是正数,那么-a一定是负数( )
④不存在既不是正数,也不是负数的数( )
②带“+”号的数都是正数 ( )
×
×
×
×
×
√
1)判断题:
1.有理数的分类
练习巩固
3)填空:
最小的自然数是 ,
最大的负整数是 ,
最小的正整数是 ,
最大的非正数是 .
2)判断:
(1)整数一定是自然数( )
(2)自然数一定是整数( )
×
√
0
-1
1
0
1.有理数的分类
4)把下列各数填在相应额大括号内:
-0.1,-789,25,0,-20,-3.14, ,5.3.
正有理数集 { …}
负有理数集{ …}
整数集{ …}
4
5
-0.1,
-789,
25,
-20,
-3.14,
5.3,
25,
0,
4
5
-789,
-20,
,
1.有理数的分类
2.与原点的距离为三个单位的点有__个,他们分别表
示的有理数是 和 .
+3
-3
2
3.与+3表示的点距离2000个单位的点有__个,他们
分别表示的有理数是__ __ 和 .
1.两个有理数表示较大的数的点离原点的距离较近( )
×
2
2003
-1997
4. +3表示的点与-2表示的点距离是__个单位。
5
2.数 轴
-0.5,-3.5, 2.5, ,-(-4).
0
1
2
3
-1
-2
-3
-4
4
| - |
3
2
●
●
●
●
●
-(-4)
-0.5
-3.5
2.5
| - |
3
2
| - |
3
2
-3.5
-0.5
2.5
-(-4)
>
>
>
>
画一条数轴,在数轴上标出下列各数,再将它们按由小到大的顺序用不等号连接起来.
4. 只要符号不同,这两个数就是相反数( )
2.互为相反数的两个数在数轴上位于原点两旁( )
1.一个数的相反数是最小的正整数,这个数是( )
A . -1 B. 1 C .±1 D. 0
A
×
×
3.位于原点两旁的数是互为相反数( )
5.表示相反意义的量的两个数互为相反数( )
×
×
6.若-a=-8,则-a的相反数是 ;
-(-4)的相反数是 .
8
-4
3.相反数
1)绝对值等于它本身的数是正数( )
5)任何数的绝对值都不是负数( )
2)绝对值等于它的相反数的数是负数( )
3)正数的绝对值大于负数的绝对值( )
4) 绝对值较大的数较大( )
×
×
×
×
√
4.绝对值
1)判断:
2)判断:
(1)|5|=|-5| ( )
(2)|-0.3|=|0.3| ( )
(3)|3|>0 ( )
(4)|-1.4|>0 ( )
(5)有理数的绝对值一定是正数 ( )
(6)若a=b,则|a|=|b| ( )
(7)若|a|=|b|,则a=b ( )
(8)若|a|=-a,则a必为负数 ( )
×
√
√
√
√
√
×
×
5.倒数
如果两个有理数数的乘积为1,我们称这两个有理数互为倒数.
(1) 的倒数是 ; -2的倒数是 .
① 和(-7);
②-1 和- ;
(2) 下列各组数中,互为倒数的有( ).
A.3组 B.4组 C.5组 D.6组
③-|-4|和- ;
④ 0和0
⑤1 和-1;
⑥3.2和 .
1
7
1
5
5
6
1
4
5
16
2
5
5
2
1
2
-
A
6.科学记数法
梧州市是世界最大的人工宝石加工集聚基地,年产量达约12 000 000 000粒,市场份额占全国产量的80%、世界产量的70%,被誉为“世界人工宝石之都”.请你将12 000 000 000用科学记数法表示为 ( )
A.12×109 B.1.2×1010
C.0.12×1011 D.120×108
B
7.近似数
下列说法正确的是( ).
A.0.720精确到百分位
B.3.6万精确到个位
C.5.078精确到千分位
D.8.66×106精确到百分位
C
8.已知a,b互为相反数,c,d互为倒数,
|m| =4,求 +cd +m的值.
a+b
m
解:
因为a,b互为相反数,
所以a+b=0.
因为c,d互为倒数,
所以cd=1.
因为|m| =4,
所以m=±4.
当m=4时,
+cd +m=
a+b
m
0
4
+1 +4
=5.
当m=-4时,
+ cd +m=
a+ b
m
0
-4
+1-4
=-3.
所以
+cd +m的值为
a+ b
m
5或-3.
9.如果| a |=8,|b|=5,且a+b<0,求a-b的值.
解:
因为| a |=8,
所以a=8
或a=-8,
因为| b |=5,
所以b=5
或b=-5,
因为a+b<0,
所以a= - 8,
b=5
或b=-5,
所以a-b=
- 8-5
= -13,
或a-b=
- 8-(-5)
= -3.
今天作业
课本P52第6题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
