2022-2023学年华师大版数学八年级上册 第12章整式的乘除复习与测试(含答案)
文档属性
| 名称 | 2022-2023学年华师大版数学八年级上册 第12章整式的乘除复习与测试(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 292.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 00:00:00 | ||
图片预览



文档简介
第12章复习与测试
1.已知10x=a,5x=b,求:
(1)50x的值;
(2)2x的值;
(3)20x的值.(结果用含a、b的代数式表示)
2.若am=an(a>0,a≠1,m、n都是正整数),则m=n,利用上面结论解决下面的问题:
(1)如果2x 23=32,求x的值;
(2)如果2÷8x 16x=25,求x的值;
(3)若x=5m﹣2,y=3﹣25m,用含x的代数式表示y.
3.已知x3m=2,y2m=3,求(x2m)3+(ym)6﹣(x2y)3m ym的值.
4.计算:a2b4 (﹣ab)2+a (﹣2ab2)3.
5.(﹣x3)2×(﹣2x3)﹣(x5)3÷(﹣x3)2.
6.计算:
(1)(a3)2÷a4 a;
(2)x6÷(x4÷x2);
(3)2a3+a6÷(﹣a)3;
(4)(﹣5a3)2+(﹣3a2)2 (﹣a2).
7.规定两数a,b之间的一种运算,记作(a,b);如果ac=b,那么(a,b)=c.
例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:
①(4,16)= ,(﹣3,81)= ;
②若(x,)=﹣4,则x= .
(2)小明在研究这种运算时发现一个特征:(3n,4n)=(3,4),小明给出了如下的证明:
设(3n,4n)=x,则(3n)x=4n,即(3x)n=4n,所以3x=4,即(3,4)=x,
所以(3n,4n)=(3,4).试解决下列问题:.
①计算(9,100)﹣(81,10000)
②若(16,49)=a,(4,3)=b,(16,441)=c,请探索a,b,c之间的数量关系.
8.计算:(﹣a)2 (﹣a3) (﹣a)+(﹣a2)3﹣(﹣a3)2.
9.(1)如图是小颖家新房的户型图,小颖的爸爸打算把两个卧室以外的部分都铺上地砖,至少需要多少平方米的地砖?如果某种地砖的价格为每平方米a元,那么购买地砖至少需要多少元?
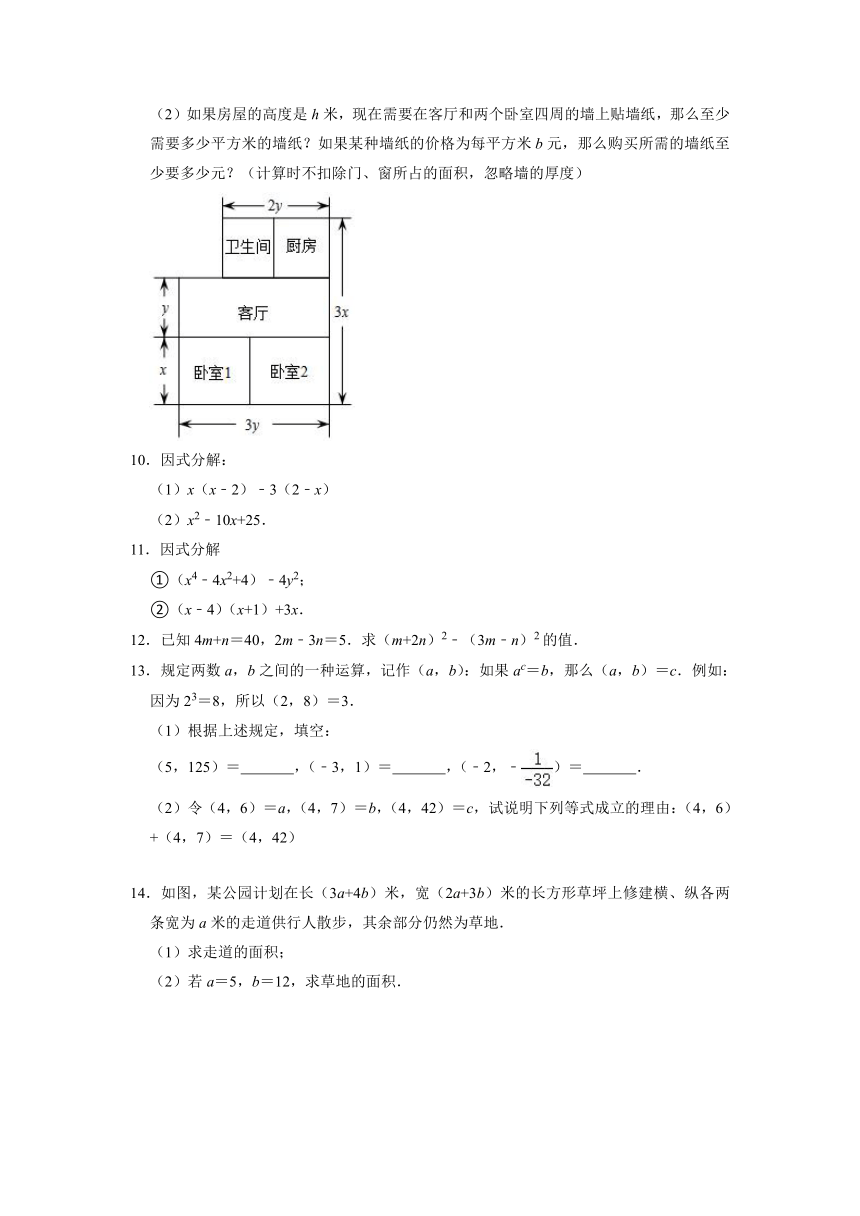
(2)如果房屋的高度是h米,现在需要在客厅和两个卧室四周的墙上贴墙纸,那么至少需要多少平方米的墙纸?如果某种墙纸的价格为每平方米b元,那么购买所需的墙纸至少要多少元?(计算时不扣除门、窗所占的面积,忽略墙的厚度)
10.因式分解:
(1)x(x﹣2)﹣3(2﹣x)
(2)x2﹣10x+25.
11.因式分解
①(x4﹣4x2+4)﹣4y2;
②(x﹣4)(x+1)+3x.
12.已知4m+n=40,2m﹣3n=5.求(m+2n)2﹣(3m﹣n)2的值.
13.规定两数a,b之间的一种运算,记作(a,b):如果ac=b,那么(a,b)=c.例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:
(5,125)= ,(﹣3,1)= ,(﹣2,﹣)= .
(2)令(4,6)=a,(4,7)=b,(4,42)=c,试说明下列等式成立的理由:(4,6)+(4,7)=(4,42)
14.如图,某公园计划在长(3a+4b)米,宽(2a+3b)米的长方形草坪上修建横、纵各两条宽为a米的走道供行人散步,其余部分仍然为草地.
(1)求走道的面积;
(2)若a=5,b=12,求草地的面积.
15.小明学习了“第八章幂的运算”后做这样一道题:若(2x﹣3)x+3=1,求x的值,他解出来的结果为x=1,老师说小明考虑问题不全面,聪明的你能帮助小明解决这个问题吗?小明解答过程如下:
解:因为1的任何次幂为1,所以2x﹣3=1,x=2.且2+3=5故(2x﹣3)x+3=(2×2﹣3)2+3=15=1,所以x=2.你的解答是:
16.若x满足(x﹣4)(x﹣9)=6,求(x﹣4)2+(x﹣9)2的值.阅读下面求解的方法:
解:设(x﹣4)=a,(x﹣9)=b,则ab=(x﹣4)(x﹣9)=6,a﹣b=(x﹣4)﹣(x﹣9)=5
∴(x﹣4)2+(x﹣9)2=a2+b2=(a﹣b)2+2ab=52+2×6=37.
请仿照上面的方法求解下面的问题:
(1)若x满足(x﹣2)(x﹣5)=10,求(x﹣2)2+(x﹣5)2的值;
(2)如图,正方形ABCD中,E、F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是15,分别以MF、DF为边作正方形,若AD=x,则
①DE= ,DF= (用含x的代数式表示);
②直接写出图中阴影部分的面积.
17.如图①,是一个长为2m、宽为2n的长方形,用剪刀沿图中的虚线(对称轴)剪开,把它分成四个形状和大小都相同的小长方形,然后按图②那样拼成一个正方形(中间是空的).
(1)图②中画有阴影的小正方形的边长为 (用含m,n的式子表示);
(2)观察图②,写出代数式(m+n)2,(m﹣n)2与mn之间的等量关系;
(3)根据(2)中的等量关系解决下面的问题:
(i)若m+n=7,mn=5,求(m﹣n)2的值;
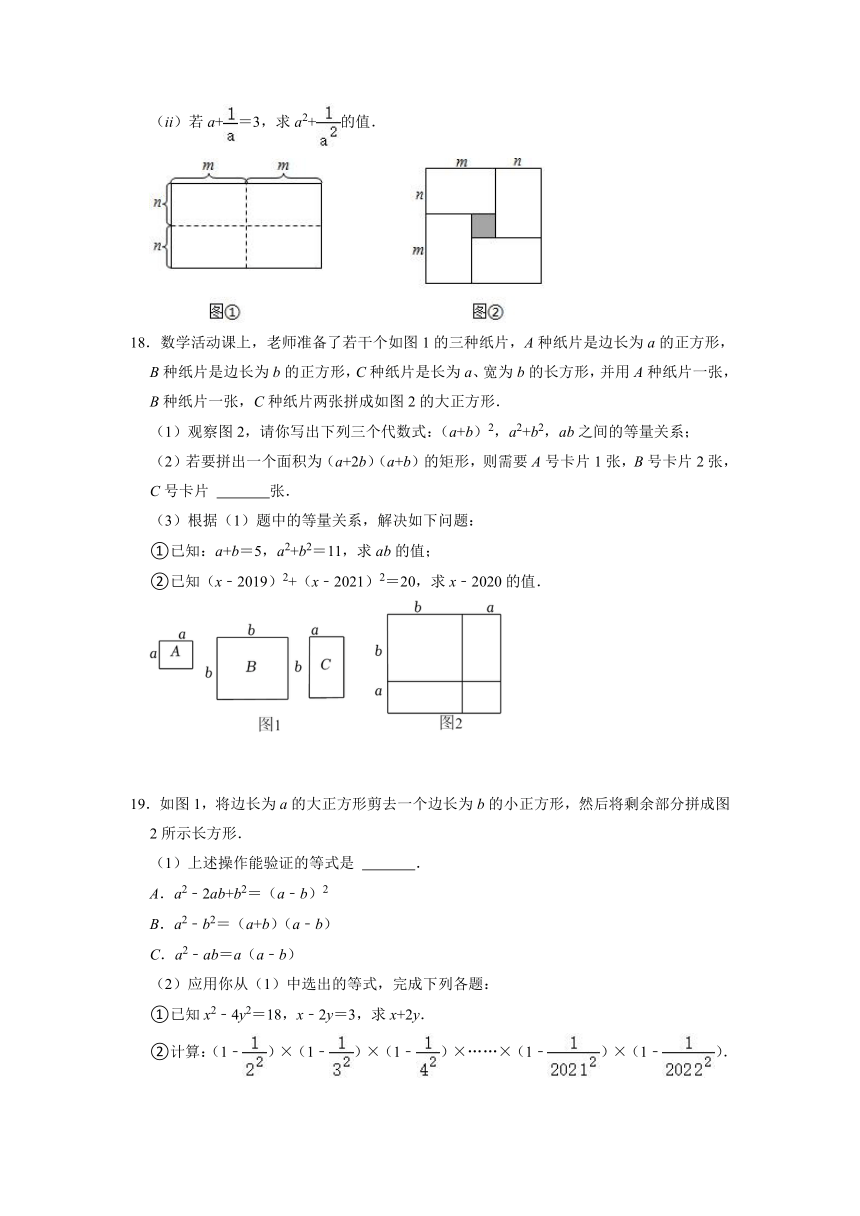
(ii)若a+=3,求a2+的值.
18.数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为a、宽为b的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系;
(2)若要拼出一个面积为(a+2b)(a+b)的矩形,则需要A号卡片1张,B号卡片2张,C号卡片 张.
(3)根据(1)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=11,求ab的值;
②已知(x﹣2019)2+(x﹣2021)2=20,求x﹣2020的值.
19.如图1,将边长为a的大正方形剪去一个边长为b的小正方形,然后将剩余部分拼成图2所示长方形.
(1)上述操作能验证的等式是 .
A.a2﹣2ab+b2=(a﹣b)2
B.a2﹣b2=(a+b)(a﹣b)
C.a2﹣ab=a(a﹣b)
(2)应用你从(1)中选出的等式,完成下列各题:
①已知x2﹣4y2=18,x﹣2y=3,求x+2y.
②计算:(1﹣)×(1﹣)×(1﹣)×……×(1﹣)×(1﹣).
20.下面是某同学对多项式(x2﹣4x+2)(x2﹣4x+6)+4进行因式分解的过程.
解:设x2﹣4x=y
原式=(y+2)(y+6)+4(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
=(x2﹣4x+4)2(第四步)
请问:
(1)该同学因式分解的结果是否彻底? (填“彻底”或“不彻底”).若不彻底,请直接写出因式分解的最后结果.
(2)请你模仿以上方法尝试对多项式(x2﹣2x)(x2﹣2x+2)+1进行因式分解.
参考答案
1.解:(1)50x=10x×5x=ab;
(2)2x===;
(3)20x===.
2.解:(1)∵2x 23=32,
∴2x+3=25,
∴x+3=5,
∴x=2;
(2)∵2÷8x 16x=25,
∴2÷23x 24x=25,
∴21﹣3x+4x=25,
∴1+x=5,
∴x=4;
(3)∵x=5m﹣2,
∴5m=x+2,
∵y=3﹣25m,
∴y=3﹣(5m)2,
∴y=3﹣(x+2)2=﹣x2﹣4x﹣1.
3.解:∵x3m=2,y2m=3,
∴(x2m)3+(ym)6﹣(x2y)3m ym
=(x3m)2+(y2m)3﹣(x6my3m×ym)
=(x3m)2+(y2m)3﹣(x3my2m)2
=22+33﹣(2×3)2
=﹣5.
4.解:原式=a2b4 (﹣ab)2+a (﹣2ab2)3
=a4b6﹣2a4b6
=﹣a4b6.
5.解:原式=x6×(﹣2x3)﹣x15÷x6
=﹣x9﹣x9
=﹣x9.
6.解:(1)(a3)2÷a4 a
=a6÷a4 a
=a2 a
=a3;
(2)x6÷(x4÷x2)
=x6÷x2
=x4;
(3)2a3+a6÷(﹣a)3
=2a3﹣a3
=a3;
(4)(﹣5a3)2+(﹣3a2)2 (﹣a2)
=25a6+9a4 (﹣a2)
=25a6﹣9a6
=16a6.
7.解:(1)①∵42=16,
∴(4,16)=2,
∵(﹣3)4=81,
∴(﹣3,81)=4,
故答案为:2,4;
②由题意得:,
∴,
∴x=±2,
故答案为:±2;
(2)①(9,100)﹣(81,10000)
=(32,102)﹣(34,104)
=(3,10)﹣(3,10)
=0;
②∵(16,49)=a,(16,441)=c,
∴(4,7)=a,(4,21)=c,
∴4a=7,4c=21,4b=3,
∵4c=3×7=4a×4b,
∴c=a+b.
8.解:原式=a2 (﹣a3) (﹣a)+(﹣a6)﹣a6
=a6﹣a6﹣a6
=﹣a6.
9.解:(1)由题意知,两个卧室以外的部分面积为:
3y y+2y (3x﹣x﹣y)
=3y2+4xy﹣2y2
=y2+4xy(平方米).
∴购买地砖所需的费用为:(y2+4xy)a=ay2+4axy(元).
(2)客厅贴墙纸的面积为:(2y+6y)h=8yh,
两个卧室贴墙纸的面积为:(4x+6y)h=4xh+6yh,
∴贴墙纸的总面积为:8yh+4xh+6yh=14yh+4xh(平方米),
∴购买墙纸所需的费用为:(14yh+4xh)b=14yhb+4xhb(元).
10.解:(1)原式=x(x﹣2)+3(x﹣2)=(x﹣2)(x+3);
(2)原式=(x﹣5)2.
11.解:(1)原式=(x2﹣2)2﹣4y2
=(x2﹣2+2y)(x2﹣2﹣2y);
(2)原式=x2﹣3x﹣4+3x
=x2﹣4
=(x+2)(x﹣2).
12.解:(m+2n)2﹣(3m﹣n)2
=(m+2n+3m﹣n)(m+2n﹣3m+n)
=(4m+n)(3n﹣2m)
=﹣(4m+n)(2m﹣3n),
当4m+n=40,2m﹣3n=5时,原式=﹣40×5=﹣200.
13.解:(1)∵如果ac=b,那么(a,b)=c,53=125,(﹣3)0=1,(﹣2)﹣5=,
∴(5,125)=3,(﹣3,1)=0,(﹣2,﹣)=﹣5.
故答案为:3,0,﹣5.
(2)由题意得:4a=6,4b=7,4c=42.
∵42=6×7,
∴4c=4a×4b=4a+b,
∴a+b=c.
∴(4,6)+(4,7)=(4,42).
14.解:(1)∵草地的部分可以拼成一个长方形,
∴长为3a+4b﹣a﹣a=(a+4b)米,
宽为2a+3b﹣a﹣a=3b(米),
∴草地面积为(a+4b)×3b=(3ab+12b2)平方米,
∴走道面积为(3a+4b)(2a+3b)﹣(3ab+12b2),
=6a2+9ab+8ab+12b2﹣3ab﹣12b2,
=(6a2+14ab)平方米,
答:走道的面积为(6a2+14ab)平方米.
(2)由(1)可知草地面积为(a+4b)×3b=(3ab+12b2)平方米,
将a=5,b=12代入得:3×5×12+12×122=1908(平方米),
答:草地面积为1908平方米.
15.解:①∵1的任何次幂为1,所以2x﹣3=1,x=2.且2+3=5,
∴(2x﹣3)x+3=(2×2﹣3)2+3=15=1,
∴x=2;
②∵﹣1的任何偶次幂也都是1,
∴2x﹣3=﹣1,且x+3为偶数,
∴x=1,
当x=1时,x+3=4是偶数,
∴x=1;
③∵任何不是0的数的0次幂也是1,
∴x+3=0,2x﹣3≠0,
解的:x=﹣3,
综上:x=2或﹣3或1.
16.解:(1)设(x﹣2)=a,(x﹣5)=b,则ab=(x﹣2)(x﹣5)=10,a﹣b=(x﹣2)﹣(x﹣5)=3,
∴(x﹣2)2+(x﹣5)2=a2+b2=(a﹣b)2+2ab=32+2×10=29;
(2)①∵AE=1,CF=3,正方形ABCD边长为x,
∴DE=x﹣1,DF=x﹣3.
故答案为:x﹣1,x﹣3;
②∵长方形EMFD的面积是15,
∴(x﹣1)(x﹣3)=15,
设x﹣1=a,x﹣3=b,则ab=15,a﹣b=2,
∴(x﹣1+x﹣3) =(a+b) =(a﹣b) +4ab=2 +4×15=64,
∵a≥0,b≥0,
∴x﹣1+x﹣3=a+b=8,
∴阴影部分面积为(x﹣1)2﹣(x﹣3)2=a ﹣b =(a+b)(a﹣b)=16.
17.解:(1)图②中画有阴影的小正方形的边长(m﹣n);
故答案为:m﹣n.
(2)图②中画有阴影的小正方形的边长(m﹣n),面积为:(m﹣n)2,
(图②中画有阴影的小正方形的面积还可以表示为:(m+n)2﹣4mn.
∴(m﹣n)2=(m+n)2﹣4mn.
(3)(i)(m﹣n)2=(m+n)2﹣4mn=49﹣20=29.
(ii)a2+=﹣2=9﹣2=7.
18.解:(1)大正方形的面积可以表示为:(a+b)2,或表示为:a2+b2+2ab;
因此有(a+b)2=a2+b2+2ab;
(2)∵(a+2b)(a+b)=a2+3ab+2b2,
∴需要A号卡片1张,B号卡片2张,C号卡片3张,
故答案为:3;
(3)①∵(a+b)2=a2+b2+2ab,a+b=5,a2+b2=11,
∴25=11+2ab,
∴ab=7,
即ab的值为7;
②令a=x﹣2020,
∴x﹣2019
=[x﹣(2020﹣1)]
=x﹣2020+1
=a+1,
x﹣2021
=[x﹣(2020+1)]
=x﹣2020﹣1
=a﹣1,
∵(x﹣2019)2+(x﹣2021)2=20,
∴(a+1)2+(a﹣1)2=20,
解得a2=9.
∴(x﹣2020)2=9,
∴x﹣2020=±3.
19.解:(1)根据阴影部分的面积相等得出:a2﹣b2=(a+b)(a﹣b).
故选:B.
(2)①∵x2﹣4y2=18,x﹣2y=3,
∴x+2y=(x2﹣4y2)÷(x﹣2y)=18÷3=6;
②原式=(1﹣)×(1+)×(1﹣)×(1+)×……×(1﹣)×(1+)
=××××……××
=×
=.
20.解:(1)∵(x2﹣4x+4)2=(x﹣2)4,
∴该同学因式分解的结果不彻底.
(2)设x2﹣2x=y
原式=y(y+2)+1
=y2+2y+1
=(y+1)2
=(x2﹣2x+1)2
=(x﹣1)4.
故答案为:不彻底.
1.已知10x=a,5x=b,求:
(1)50x的值;
(2)2x的值;
(3)20x的值.(结果用含a、b的代数式表示)
2.若am=an(a>0,a≠1,m、n都是正整数),则m=n,利用上面结论解决下面的问题:
(1)如果2x 23=32,求x的值;
(2)如果2÷8x 16x=25,求x的值;
(3)若x=5m﹣2,y=3﹣25m,用含x的代数式表示y.
3.已知x3m=2,y2m=3,求(x2m)3+(ym)6﹣(x2y)3m ym的值.
4.计算:a2b4 (﹣ab)2+a (﹣2ab2)3.
5.(﹣x3)2×(﹣2x3)﹣(x5)3÷(﹣x3)2.
6.计算:
(1)(a3)2÷a4 a;
(2)x6÷(x4÷x2);
(3)2a3+a6÷(﹣a)3;
(4)(﹣5a3)2+(﹣3a2)2 (﹣a2).
7.规定两数a,b之间的一种运算,记作(a,b);如果ac=b,那么(a,b)=c.
例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:
①(4,16)= ,(﹣3,81)= ;
②若(x,)=﹣4,则x= .
(2)小明在研究这种运算时发现一个特征:(3n,4n)=(3,4),小明给出了如下的证明:
设(3n,4n)=x,则(3n)x=4n,即(3x)n=4n,所以3x=4,即(3,4)=x,
所以(3n,4n)=(3,4).试解决下列问题:.
①计算(9,100)﹣(81,10000)
②若(16,49)=a,(4,3)=b,(16,441)=c,请探索a,b,c之间的数量关系.
8.计算:(﹣a)2 (﹣a3) (﹣a)+(﹣a2)3﹣(﹣a3)2.
9.(1)如图是小颖家新房的户型图,小颖的爸爸打算把两个卧室以外的部分都铺上地砖,至少需要多少平方米的地砖?如果某种地砖的价格为每平方米a元,那么购买地砖至少需要多少元?
(2)如果房屋的高度是h米,现在需要在客厅和两个卧室四周的墙上贴墙纸,那么至少需要多少平方米的墙纸?如果某种墙纸的价格为每平方米b元,那么购买所需的墙纸至少要多少元?(计算时不扣除门、窗所占的面积,忽略墙的厚度)
10.因式分解:
(1)x(x﹣2)﹣3(2﹣x)
(2)x2﹣10x+25.
11.因式分解
①(x4﹣4x2+4)﹣4y2;
②(x﹣4)(x+1)+3x.
12.已知4m+n=40,2m﹣3n=5.求(m+2n)2﹣(3m﹣n)2的值.
13.规定两数a,b之间的一种运算,记作(a,b):如果ac=b,那么(a,b)=c.例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:
(5,125)= ,(﹣3,1)= ,(﹣2,﹣)= .
(2)令(4,6)=a,(4,7)=b,(4,42)=c,试说明下列等式成立的理由:(4,6)+(4,7)=(4,42)
14.如图,某公园计划在长(3a+4b)米,宽(2a+3b)米的长方形草坪上修建横、纵各两条宽为a米的走道供行人散步,其余部分仍然为草地.
(1)求走道的面积;
(2)若a=5,b=12,求草地的面积.
15.小明学习了“第八章幂的运算”后做这样一道题:若(2x﹣3)x+3=1,求x的值,他解出来的结果为x=1,老师说小明考虑问题不全面,聪明的你能帮助小明解决这个问题吗?小明解答过程如下:
解:因为1的任何次幂为1,所以2x﹣3=1,x=2.且2+3=5故(2x﹣3)x+3=(2×2﹣3)2+3=15=1,所以x=2.你的解答是:
16.若x满足(x﹣4)(x﹣9)=6,求(x﹣4)2+(x﹣9)2的值.阅读下面求解的方法:
解:设(x﹣4)=a,(x﹣9)=b,则ab=(x﹣4)(x﹣9)=6,a﹣b=(x﹣4)﹣(x﹣9)=5
∴(x﹣4)2+(x﹣9)2=a2+b2=(a﹣b)2+2ab=52+2×6=37.
请仿照上面的方法求解下面的问题:
(1)若x满足(x﹣2)(x﹣5)=10,求(x﹣2)2+(x﹣5)2的值;
(2)如图,正方形ABCD中,E、F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是15,分别以MF、DF为边作正方形,若AD=x,则
①DE= ,DF= (用含x的代数式表示);
②直接写出图中阴影部分的面积.
17.如图①,是一个长为2m、宽为2n的长方形,用剪刀沿图中的虚线(对称轴)剪开,把它分成四个形状和大小都相同的小长方形,然后按图②那样拼成一个正方形(中间是空的).
(1)图②中画有阴影的小正方形的边长为 (用含m,n的式子表示);
(2)观察图②,写出代数式(m+n)2,(m﹣n)2与mn之间的等量关系;
(3)根据(2)中的等量关系解决下面的问题:
(i)若m+n=7,mn=5,求(m﹣n)2的值;
(ii)若a+=3,求a2+的值.
18.数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为a、宽为b的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系;
(2)若要拼出一个面积为(a+2b)(a+b)的矩形,则需要A号卡片1张,B号卡片2张,C号卡片 张.
(3)根据(1)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=11,求ab的值;
②已知(x﹣2019)2+(x﹣2021)2=20,求x﹣2020的值.
19.如图1,将边长为a的大正方形剪去一个边长为b的小正方形,然后将剩余部分拼成图2所示长方形.
(1)上述操作能验证的等式是 .
A.a2﹣2ab+b2=(a﹣b)2
B.a2﹣b2=(a+b)(a﹣b)
C.a2﹣ab=a(a﹣b)
(2)应用你从(1)中选出的等式,完成下列各题:
①已知x2﹣4y2=18,x﹣2y=3,求x+2y.
②计算:(1﹣)×(1﹣)×(1﹣)×……×(1﹣)×(1﹣).
20.下面是某同学对多项式(x2﹣4x+2)(x2﹣4x+6)+4进行因式分解的过程.
解:设x2﹣4x=y
原式=(y+2)(y+6)+4(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
=(x2﹣4x+4)2(第四步)
请问:
(1)该同学因式分解的结果是否彻底? (填“彻底”或“不彻底”).若不彻底,请直接写出因式分解的最后结果.
(2)请你模仿以上方法尝试对多项式(x2﹣2x)(x2﹣2x+2)+1进行因式分解.
参考答案
1.解:(1)50x=10x×5x=ab;
(2)2x===;
(3)20x===.
2.解:(1)∵2x 23=32,
∴2x+3=25,
∴x+3=5,
∴x=2;
(2)∵2÷8x 16x=25,
∴2÷23x 24x=25,
∴21﹣3x+4x=25,
∴1+x=5,
∴x=4;
(3)∵x=5m﹣2,
∴5m=x+2,
∵y=3﹣25m,
∴y=3﹣(5m)2,
∴y=3﹣(x+2)2=﹣x2﹣4x﹣1.
3.解:∵x3m=2,y2m=3,
∴(x2m)3+(ym)6﹣(x2y)3m ym
=(x3m)2+(y2m)3﹣(x6my3m×ym)
=(x3m)2+(y2m)3﹣(x3my2m)2
=22+33﹣(2×3)2
=﹣5.
4.解:原式=a2b4 (﹣ab)2+a (﹣2ab2)3
=a4b6﹣2a4b6
=﹣a4b6.
5.解:原式=x6×(﹣2x3)﹣x15÷x6
=﹣x9﹣x9
=﹣x9.
6.解:(1)(a3)2÷a4 a
=a6÷a4 a
=a2 a
=a3;
(2)x6÷(x4÷x2)
=x6÷x2
=x4;
(3)2a3+a6÷(﹣a)3
=2a3﹣a3
=a3;
(4)(﹣5a3)2+(﹣3a2)2 (﹣a2)
=25a6+9a4 (﹣a2)
=25a6﹣9a6
=16a6.
7.解:(1)①∵42=16,
∴(4,16)=2,
∵(﹣3)4=81,
∴(﹣3,81)=4,
故答案为:2,4;
②由题意得:,
∴,
∴x=±2,
故答案为:±2;
(2)①(9,100)﹣(81,10000)
=(32,102)﹣(34,104)
=(3,10)﹣(3,10)
=0;
②∵(16,49)=a,(16,441)=c,
∴(4,7)=a,(4,21)=c,
∴4a=7,4c=21,4b=3,
∵4c=3×7=4a×4b,
∴c=a+b.
8.解:原式=a2 (﹣a3) (﹣a)+(﹣a6)﹣a6
=a6﹣a6﹣a6
=﹣a6.
9.解:(1)由题意知,两个卧室以外的部分面积为:
3y y+2y (3x﹣x﹣y)
=3y2+4xy﹣2y2
=y2+4xy(平方米).
∴购买地砖所需的费用为:(y2+4xy)a=ay2+4axy(元).
(2)客厅贴墙纸的面积为:(2y+6y)h=8yh,
两个卧室贴墙纸的面积为:(4x+6y)h=4xh+6yh,
∴贴墙纸的总面积为:8yh+4xh+6yh=14yh+4xh(平方米),
∴购买墙纸所需的费用为:(14yh+4xh)b=14yhb+4xhb(元).
10.解:(1)原式=x(x﹣2)+3(x﹣2)=(x﹣2)(x+3);
(2)原式=(x﹣5)2.
11.解:(1)原式=(x2﹣2)2﹣4y2
=(x2﹣2+2y)(x2﹣2﹣2y);
(2)原式=x2﹣3x﹣4+3x
=x2﹣4
=(x+2)(x﹣2).
12.解:(m+2n)2﹣(3m﹣n)2
=(m+2n+3m﹣n)(m+2n﹣3m+n)
=(4m+n)(3n﹣2m)
=﹣(4m+n)(2m﹣3n),
当4m+n=40,2m﹣3n=5时,原式=﹣40×5=﹣200.
13.解:(1)∵如果ac=b,那么(a,b)=c,53=125,(﹣3)0=1,(﹣2)﹣5=,
∴(5,125)=3,(﹣3,1)=0,(﹣2,﹣)=﹣5.
故答案为:3,0,﹣5.
(2)由题意得:4a=6,4b=7,4c=42.
∵42=6×7,
∴4c=4a×4b=4a+b,
∴a+b=c.
∴(4,6)+(4,7)=(4,42).
14.解:(1)∵草地的部分可以拼成一个长方形,
∴长为3a+4b﹣a﹣a=(a+4b)米,
宽为2a+3b﹣a﹣a=3b(米),
∴草地面积为(a+4b)×3b=(3ab+12b2)平方米,
∴走道面积为(3a+4b)(2a+3b)﹣(3ab+12b2),
=6a2+9ab+8ab+12b2﹣3ab﹣12b2,
=(6a2+14ab)平方米,
答:走道的面积为(6a2+14ab)平方米.
(2)由(1)可知草地面积为(a+4b)×3b=(3ab+12b2)平方米,
将a=5,b=12代入得:3×5×12+12×122=1908(平方米),
答:草地面积为1908平方米.
15.解:①∵1的任何次幂为1,所以2x﹣3=1,x=2.且2+3=5,
∴(2x﹣3)x+3=(2×2﹣3)2+3=15=1,
∴x=2;
②∵﹣1的任何偶次幂也都是1,
∴2x﹣3=﹣1,且x+3为偶数,
∴x=1,
当x=1时,x+3=4是偶数,
∴x=1;
③∵任何不是0的数的0次幂也是1,
∴x+3=0,2x﹣3≠0,
解的:x=﹣3,
综上:x=2或﹣3或1.
16.解:(1)设(x﹣2)=a,(x﹣5)=b,则ab=(x﹣2)(x﹣5)=10,a﹣b=(x﹣2)﹣(x﹣5)=3,
∴(x﹣2)2+(x﹣5)2=a2+b2=(a﹣b)2+2ab=32+2×10=29;
(2)①∵AE=1,CF=3,正方形ABCD边长为x,
∴DE=x﹣1,DF=x﹣3.
故答案为:x﹣1,x﹣3;
②∵长方形EMFD的面积是15,
∴(x﹣1)(x﹣3)=15,
设x﹣1=a,x﹣3=b,则ab=15,a﹣b=2,
∴(x﹣1+x﹣3) =(a+b) =(a﹣b) +4ab=2 +4×15=64,
∵a≥0,b≥0,
∴x﹣1+x﹣3=a+b=8,
∴阴影部分面积为(x﹣1)2﹣(x﹣3)2=a ﹣b =(a+b)(a﹣b)=16.
17.解:(1)图②中画有阴影的小正方形的边长(m﹣n);
故答案为:m﹣n.
(2)图②中画有阴影的小正方形的边长(m﹣n),面积为:(m﹣n)2,
(图②中画有阴影的小正方形的面积还可以表示为:(m+n)2﹣4mn.
∴(m﹣n)2=(m+n)2﹣4mn.
(3)(i)(m﹣n)2=(m+n)2﹣4mn=49﹣20=29.
(ii)a2+=﹣2=9﹣2=7.
18.解:(1)大正方形的面积可以表示为:(a+b)2,或表示为:a2+b2+2ab;
因此有(a+b)2=a2+b2+2ab;
(2)∵(a+2b)(a+b)=a2+3ab+2b2,
∴需要A号卡片1张,B号卡片2张,C号卡片3张,
故答案为:3;
(3)①∵(a+b)2=a2+b2+2ab,a+b=5,a2+b2=11,
∴25=11+2ab,
∴ab=7,
即ab的值为7;
②令a=x﹣2020,
∴x﹣2019
=[x﹣(2020﹣1)]
=x﹣2020+1
=a+1,
x﹣2021
=[x﹣(2020+1)]
=x﹣2020﹣1
=a﹣1,
∵(x﹣2019)2+(x﹣2021)2=20,
∴(a+1)2+(a﹣1)2=20,
解得a2=9.
∴(x﹣2020)2=9,
∴x﹣2020=±3.
19.解:(1)根据阴影部分的面积相等得出:a2﹣b2=(a+b)(a﹣b).
故选:B.
(2)①∵x2﹣4y2=18,x﹣2y=3,
∴x+2y=(x2﹣4y2)÷(x﹣2y)=18÷3=6;
②原式=(1﹣)×(1+)×(1﹣)×(1+)×……×(1﹣)×(1+)
=××××……××
=×
=.
20.解:(1)∵(x2﹣4x+4)2=(x﹣2)4,
∴该同学因式分解的结果不彻底.
(2)设x2﹣2x=y
原式=y(y+2)+1
=y2+2y+1
=(y+1)2
=(x2﹣2x+1)2
=(x﹣1)4.
故答案为:不彻底.
