2022-2023学年苏科版数学八年级上册 第2章 轴对称图形 复习与测试(含答案)
文档属性
| 名称 | 2022-2023学年苏科版数学八年级上册 第2章 轴对称图形 复习与测试(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 188.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 19:18:01 | ||
图片预览

文档简介
第2章复习与测试
一、选择题(每题3分,共30分)
1.下列说法中正确的个数是( )
(1)轴对称图形只有一条对称轴。(2)两个图形成轴对称,则这两个图形是全等图形。(3)全等的两个图形一定成轴对称。(4)轴对称图形指一个图形,而轴对称指两个图形。(5)两个图形关于某直线对称,对称点一定在直线的两旁。(6)轴对称图形的对称轴是一条线段。(7)若A、B关于直线MN对称,则AB垂直平分MN。
A、2 B、3 C、4 D、5
2.下列图形中对称轴条数最多的是( )
A、线段 B、等边三角形 C、正方形 D、钝角三角形
3.如图,在RtΔABC中,∠B=90 ,ED是AC的垂直平分线,
交AC于点D,交BC于点E,∠BAE=10 ,则∠C的度数是( )
A、30 B、40 C、50 D、60
4.如图,D是线段AB、BC垂直平分线的交点,若∠ABC=150 ,则∠ADC的大小是( )
A、60 B、70 C、75 D、80
5.如图,在ΔABC中,变AB的垂直平分线分别交AB、BC于点D、E,变AC的垂直平分线分别交AC、BC于点F、G,如BC=4,则ΔAEG的周长为( )
A、12 B、10 C、8 D、4
6.如图,点A、B、C表示某公司三个车间的位置,现在要建一个仓库,要求它到三个车间的距离相等,则仓库应建在( )
A、ΔABC三边中线的交点上 B、ΔABC三内角平分线交点上
C、ΔABC三条高的交点上 D、ΔABC三边垂直平分线的交点上
第4题 第5题 第6题
7.桌面上有A、B两球,若要将B球射向桌面任意一边,使一次反弹后击中A球,则如图所示8个点中,可以瞄准的点有几( )个。
A、1 B、2 C、4 D、6
8.如图,在△ABC中,点D、E、F分别在边BC、AB、AC上,且BD=BE,CD=CF,∠A=70°,那么∠FDE=________。
9.等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为( )
A、60 B、120 C、60 或120 D、60 或150
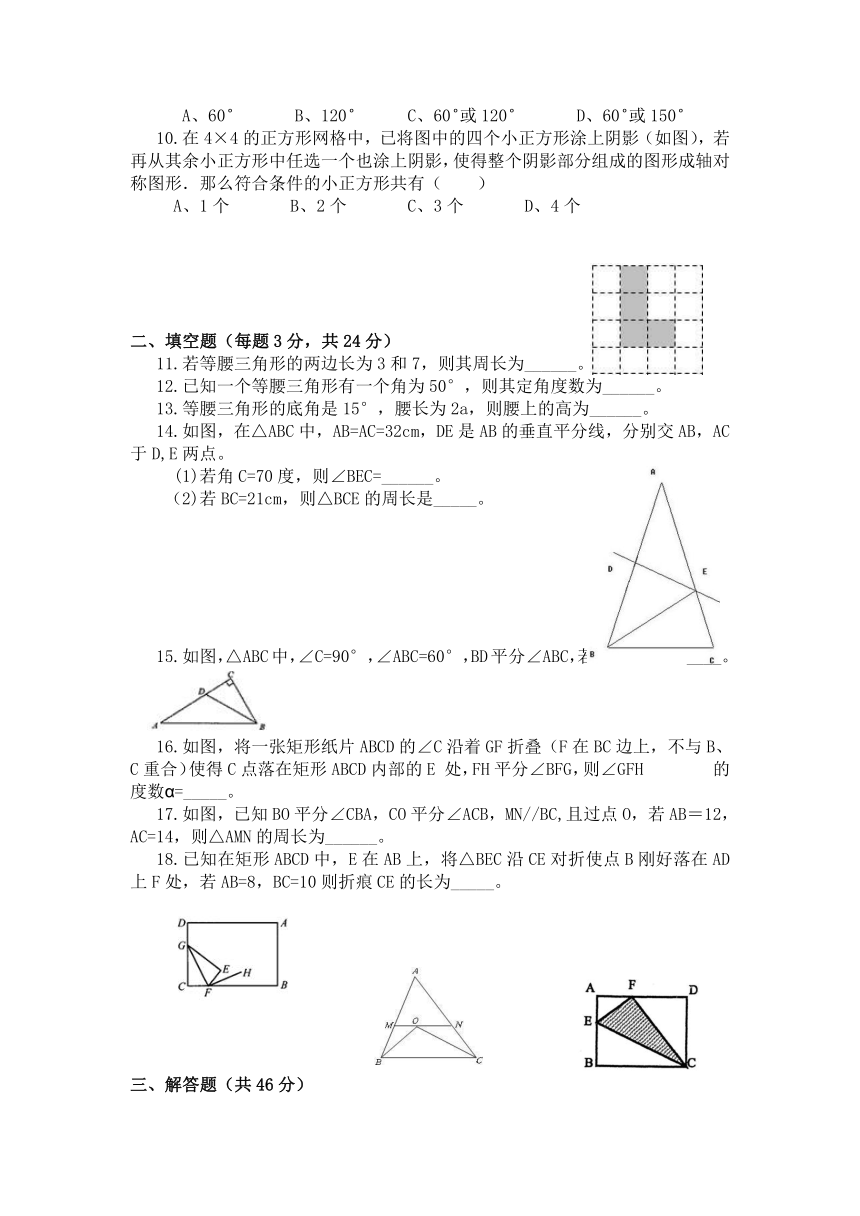
10.在4×4的正方形网格中,已将图中的四个小正方形涂上阴影(如图),若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形成轴对称图形.那么符合条件的小正方形共有( )
A、1个 B、2个 C、3个 D、4个
二、填空题(每题3分,共24分)
11.若等腰三角形的两边长为3和7,则其周长为______。
12.已知一个等腰三角形有一个角为50°,则其定角度数为______。
13.等腰三角形的底角是15°,腰长为2a,则腰上的高为______。
14.如图,在△ABC中,AB=AC=32cm,DE是AB的垂直平分线,分别交AB,AC 于D,E两点。
(1)若角C=70度,则∠BEC=______。
(2)若BC=21cm,则△BCE的周长是_____。
15.如图,△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=6,则CD=____。
16.如图,将一张矩形纸片ABCD的∠C沿着GF折叠(F在BC边上,不与B、 C重合)使得C点落在矩形ABCD内部的E 处,FH平分∠BFG,则∠GFH 的度数α=_____。
17.如图,已知BO平分∠CBA,CO平分∠ACB,MN//BC,且过点O,若AB=12,AC=14,则△AMN的周长为______。
18.已知在矩形ABCD中,E在AB上,将△BEC沿CE对折使点B刚好落在AD上F处,若AB=8,BC=10则折痕CE的长为_____。
三、解答题(共46分)
19.(12分)如图:在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点.
(1)写出点O到△ABC的三个顶点A、B、C距离之间的关系;
(2)如果点M、N分别在线段AB、AC上移动,移动中保持AN=BM,请判断△ OMN的形状,并证明你的结论.
20.(10分)如图,在△ABC中,∠C=90度,AD是∠BAC的平分线,DE⊥AB于点E,点F在AC上,BE=CF,求证:BD=DF
21.(10分)如图,在△ABC中,∠BAC=90°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA,试求∠DAE的度数。
23.(14分),如图,点E是等边△ABC内一点,且EA=EB,△ABC外一点D满足BD=AC,且BE平分∠DBC,求∠BDE的度数。
参考答案
1.A 2.C 3.B 4.A 5.D 6.D 7.B 8.C 9.C 10.C
11.17 12.80°或50° 13.a 14.(1)60°(2)53
15.3 16.90° 17.26 18.5
19 (1)∵在Rt△ABC中,∠BAC=90°,O为BC的中点,
∴OA=BC=OB=OC,即OA=OB=OC;
(2)△OMN是等腰直角三角形.理由如下:
连接AO
∵AC=AB,OC=OB
∴OA=OB,∠NAO=∠B=45°,
在△AON与△BOM中
AN=BM ∠NAO=∠B OA=OB
∴△AON≌△BOM(SAS)
∴ON=OM,∠NOA=∠MOB
∴∠NOA+∠AOM=∠MOB+∠AOM
∴∠NOM=∠AOB=90°,∴△OMN是等腰直角三角形
20.证明略
21.∵AB=AC,∠BAC=90°,∴∠B=∠ACB=45°,
∵BD=BA,
∴∠BAD=∠BDA=(180°-∠B)=67.5°,
∵CE=CA,
∴∠CAE=∠E=∠ACB=22.5°
在△ABE中,∠BAE=180°-∠B-∠E=112.5°,
∴∠DAE=∠BAE-∠BAD=112.5°-67.5°=45度;
22.解:∵AD=BD ∴∠B=∠1
∵∠ADC=∠B+∠1 ∴∠ADC=2∠1
∵AC=CD ∴∠2=∠ADC=2∠1
∵∠B=∠C ∴5∠1=180° ∴∠1=36° ∴∠BAC=108°
23.解:连接CE,
∵AC=BC,AE=BE,CE为公共边,
∴△BCE≌△ACE,
∴∠BCE=∠ACE=30°
又BD=AC=BC,∠DBE=∠CBE,BE为公共边,
∴△BDE≌△BCE,
∴∠BDE=∠BCE=30°
一、选择题(每题3分,共30分)
1.下列说法中正确的个数是( )
(1)轴对称图形只有一条对称轴。(2)两个图形成轴对称,则这两个图形是全等图形。(3)全等的两个图形一定成轴对称。(4)轴对称图形指一个图形,而轴对称指两个图形。(5)两个图形关于某直线对称,对称点一定在直线的两旁。(6)轴对称图形的对称轴是一条线段。(7)若A、B关于直线MN对称,则AB垂直平分MN。
A、2 B、3 C、4 D、5
2.下列图形中对称轴条数最多的是( )
A、线段 B、等边三角形 C、正方形 D、钝角三角形
3.如图,在RtΔABC中,∠B=90 ,ED是AC的垂直平分线,
交AC于点D,交BC于点E,∠BAE=10 ,则∠C的度数是( )
A、30 B、40 C、50 D、60
4.如图,D是线段AB、BC垂直平分线的交点,若∠ABC=150 ,则∠ADC的大小是( )
A、60 B、70 C、75 D、80
5.如图,在ΔABC中,变AB的垂直平分线分别交AB、BC于点D、E,变AC的垂直平分线分别交AC、BC于点F、G,如BC=4,则ΔAEG的周长为( )
A、12 B、10 C、8 D、4
6.如图,点A、B、C表示某公司三个车间的位置,现在要建一个仓库,要求它到三个车间的距离相等,则仓库应建在( )
A、ΔABC三边中线的交点上 B、ΔABC三内角平分线交点上
C、ΔABC三条高的交点上 D、ΔABC三边垂直平分线的交点上
第4题 第5题 第6题
7.桌面上有A、B两球,若要将B球射向桌面任意一边,使一次反弹后击中A球,则如图所示8个点中,可以瞄准的点有几( )个。
A、1 B、2 C、4 D、6
8.如图,在△ABC中,点D、E、F分别在边BC、AB、AC上,且BD=BE,CD=CF,∠A=70°,那么∠FDE=________。
9.等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为( )
A、60 B、120 C、60 或120 D、60 或150
10.在4×4的正方形网格中,已将图中的四个小正方形涂上阴影(如图),若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形成轴对称图形.那么符合条件的小正方形共有( )
A、1个 B、2个 C、3个 D、4个
二、填空题(每题3分,共24分)
11.若等腰三角形的两边长为3和7,则其周长为______。
12.已知一个等腰三角形有一个角为50°,则其定角度数为______。
13.等腰三角形的底角是15°,腰长为2a,则腰上的高为______。
14.如图,在△ABC中,AB=AC=32cm,DE是AB的垂直平分线,分别交AB,AC 于D,E两点。
(1)若角C=70度,则∠BEC=______。
(2)若BC=21cm,则△BCE的周长是_____。
15.如图,△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=6,则CD=____。
16.如图,将一张矩形纸片ABCD的∠C沿着GF折叠(F在BC边上,不与B、 C重合)使得C点落在矩形ABCD内部的E 处,FH平分∠BFG,则∠GFH 的度数α=_____。
17.如图,已知BO平分∠CBA,CO平分∠ACB,MN//BC,且过点O,若AB=12,AC=14,则△AMN的周长为______。
18.已知在矩形ABCD中,E在AB上,将△BEC沿CE对折使点B刚好落在AD上F处,若AB=8,BC=10则折痕CE的长为_____。
三、解答题(共46分)
19.(12分)如图:在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点.
(1)写出点O到△ABC的三个顶点A、B、C距离之间的关系;
(2)如果点M、N分别在线段AB、AC上移动,移动中保持AN=BM,请判断△ OMN的形状,并证明你的结论.
20.(10分)如图,在△ABC中,∠C=90度,AD是∠BAC的平分线,DE⊥AB于点E,点F在AC上,BE=CF,求证:BD=DF
21.(10分)如图,在△ABC中,∠BAC=90°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA,试求∠DAE的度数。
23.(14分),如图,点E是等边△ABC内一点,且EA=EB,△ABC外一点D满足BD=AC,且BE平分∠DBC,求∠BDE的度数。
参考答案
1.A 2.C 3.B 4.A 5.D 6.D 7.B 8.C 9.C 10.C
11.17 12.80°或50° 13.a 14.(1)60°(2)53
15.3 16.90° 17.26 18.5
19 (1)∵在Rt△ABC中,∠BAC=90°,O为BC的中点,
∴OA=BC=OB=OC,即OA=OB=OC;
(2)△OMN是等腰直角三角形.理由如下:
连接AO
∵AC=AB,OC=OB
∴OA=OB,∠NAO=∠B=45°,
在△AON与△BOM中
AN=BM ∠NAO=∠B OA=OB
∴△AON≌△BOM(SAS)
∴ON=OM,∠NOA=∠MOB
∴∠NOA+∠AOM=∠MOB+∠AOM
∴∠NOM=∠AOB=90°,∴△OMN是等腰直角三角形
20.证明略
21.∵AB=AC,∠BAC=90°,∴∠B=∠ACB=45°,
∵BD=BA,
∴∠BAD=∠BDA=(180°-∠B)=67.5°,
∵CE=CA,
∴∠CAE=∠E=∠ACB=22.5°
在△ABE中,∠BAE=180°-∠B-∠E=112.5°,
∴∠DAE=∠BAE-∠BAD=112.5°-67.5°=45度;
22.解:∵AD=BD ∴∠B=∠1
∵∠ADC=∠B+∠1 ∴∠ADC=2∠1
∵AC=CD ∴∠2=∠ADC=2∠1
∵∠B=∠C ∴5∠1=180° ∴∠1=36° ∴∠BAC=108°
23.解:连接CE,
∵AC=BC,AE=BE,CE为公共边,
∴△BCE≌△ACE,
∴∠BCE=∠ACE=30°
又BD=AC=BC,∠DBE=∠CBE,BE为公共边,
∴△BDE≌△BCE,
∴∠BDE=∠BCE=30°
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
