高中数学人教A版(2019)必修第一册 3.3 幂函数(课件)(共18张)
文档属性
| 名称 | 高中数学人教A版(2019)必修第一册 3.3 幂函数(课件)(共18张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 935.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 16:42:59 | ||
图片预览





文档简介
(共18张PPT)
3.3 幂函数
年 级:高一 学 科:数学(人教A版2019)
普通高中数学同步课件之必修一
新知讲解
一类具体函数的研究方法
创设情境
实例
如果张红以元的价格购买了某种蔬菜那么她需要支付元,这里是的函数;
如果正方形的边长为,那么正方形的面积这里是的函数;
如果立方体的棱长为,那么立方体的体积,这里是的函数;
创设情境
实例
如果一个正方形场地的面积为,那么这个正方形的边长,这里是的函数;
如果某人内骑车行进了,那么他骑车的平均速度,即,这里是的函数.
新知讲解
1 幂函数
函数叫做幂函数,其中是自变量,是常数.
小试牛刀
举例 举出几个具体的幂函数.
新知讲解
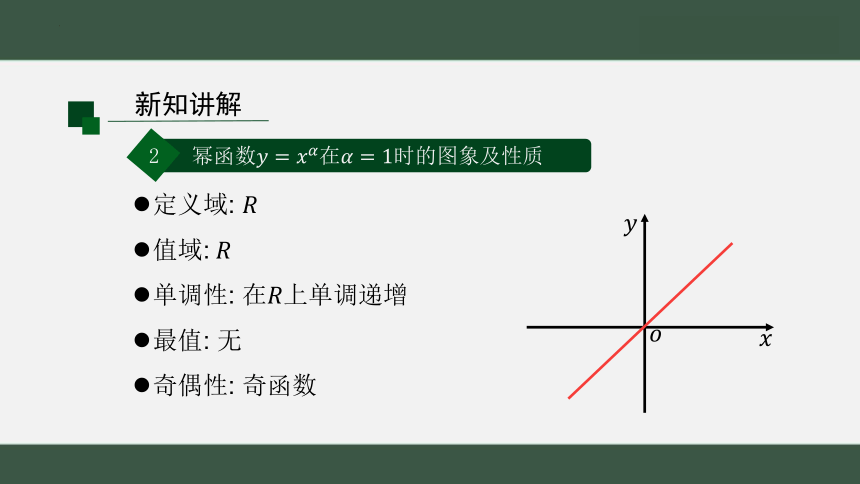
定义域:
值域:
单调性: 在上单调递增
最值: 无
奇偶性: 奇函数
2 幂函数在时的图象及性质
新知讲解
定义域:
值域:
单调性:在上单调递减
在上单调递增
最值:在时有最小值
奇偶性: 偶函数
3 幂函数在时的图象及性质
新知讲解
定义域:
值域:
单调性:在上单调递减
最值:无
奇偶性: 奇函数
4 幂函数在时的图象及性质
新知讲解
定义域:
值域:
单调性:在上单调递增
最值:在时有最小值
奇偶性: 非奇非偶函数
5 幂函数在时的图象及性质
新知讲解
定义域:
值域:
单调性:在上单调递减
在上单调递减
最值:无
奇偶性: 奇函数
6 幂函数在时的图象及性质
新知讲解
所有的幂函数在上都有定义,并且图象都过点;
当时幂函数的图象都通过原点,并且在上单调递增;
当时幂函数在上单调递减;
7 幂函数的性质
例题精讲
例 证明幂函数是增函数.
,当时,则
证明 幂函数的定义域为
例题精讲
例1 证明幂函数是增函数.
,
证明续 由且得:
所以,即.
因此,幂函数是增函数.
例2 利用幂函数的性质,比较下列各组中两个值的大小.
例题精讲
(1),
(2) ,
解 (1)函数上为增函数,且
所以,幂函数,即.
(2)函数 上为减函数,且
所以,幂函数,即.
课堂小结
1.幂函数;
2.五个具体幂函数的图象及性质;
3. 幂函数的一些性质.
作业安排
1.完成习题3.3;
2.利用对幂函数的研究过程,对函数 进行研究.
知识像一艘船让它载着我们驶向理想的
……
谢谢
3.3 幂函数
年 级:高一 学 科:数学(人教A版2019)
普通高中数学同步课件之必修一
新知讲解
一类具体函数的研究方法
创设情境
实例
如果张红以元的价格购买了某种蔬菜那么她需要支付元,这里是的函数;
如果正方形的边长为,那么正方形的面积这里是的函数;
如果立方体的棱长为,那么立方体的体积,这里是的函数;
创设情境
实例
如果一个正方形场地的面积为,那么这个正方形的边长,这里是的函数;
如果某人内骑车行进了,那么他骑车的平均速度,即,这里是的函数.
新知讲解
1 幂函数
函数叫做幂函数,其中是自变量,是常数.
小试牛刀
举例 举出几个具体的幂函数.
新知讲解
定义域:
值域:
单调性: 在上单调递增
最值: 无
奇偶性: 奇函数
2 幂函数在时的图象及性质
新知讲解
定义域:
值域:
单调性:在上单调递减
在上单调递增
最值:在时有最小值
奇偶性: 偶函数
3 幂函数在时的图象及性质
新知讲解
定义域:
值域:
单调性:在上单调递减
最值:无
奇偶性: 奇函数
4 幂函数在时的图象及性质
新知讲解
定义域:
值域:
单调性:在上单调递增
最值:在时有最小值
奇偶性: 非奇非偶函数
5 幂函数在时的图象及性质
新知讲解
定义域:
值域:
单调性:在上单调递减
在上单调递减
最值:无
奇偶性: 奇函数
6 幂函数在时的图象及性质
新知讲解
所有的幂函数在上都有定义,并且图象都过点;
当时幂函数的图象都通过原点,并且在上单调递增;
当时幂函数在上单调递减;
7 幂函数的性质
例题精讲
例 证明幂函数是增函数.
,当时,则
证明 幂函数的定义域为
例题精讲
例1 证明幂函数是增函数.
,
证明续 由且得:
所以,即.
因此,幂函数是增函数.
例2 利用幂函数的性质,比较下列各组中两个值的大小.
例题精讲
(1),
(2) ,
解 (1)函数上为增函数,且
所以,幂函数,即.
(2)函数 上为减函数,且
所以,幂函数,即.
课堂小结
1.幂函数;
2.五个具体幂函数的图象及性质;
3. 幂函数的一些性质.
作业安排
1.完成习题3.3;
2.利用对幂函数的研究过程,对函数 进行研究.
知识像一艘船让它载着我们驶向理想的
……
谢谢
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
