高中数学人教A版(2019)必修第一册 5.3诱导公式 课件-(共26张)
文档属性
| 名称 | 高中数学人教A版(2019)必修第一册 5.3诱导公式 课件-(共26张) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 16:46:43 | ||
图片预览





文档简介
(共26张PPT)
5.3 三角函数的诱导公式
(第1课时)
普通高中课程标准实验教科书·人教A版2019·数学必修第一册
复习回顾
x
y
0
P(x,y)
α的终边
1
1
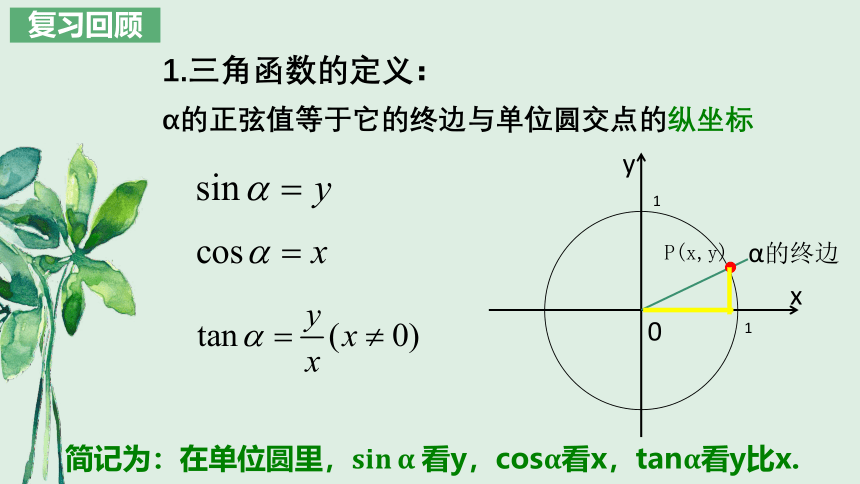
1.三角函数的定义:
α的正弦值等于它的终边与单位圆交点的纵坐标
简记为:在单位圆里,看y,cos看x,tan看y比x.
复习回顾
2. α+2kπ(k∈Z)与α的三角函数之间的关系是什么?
公式一:
( )
作用:将任意角转化为0到2范围内的角.
发现问题
3.你能求sin750°和sin930°的值吗?
=
本节要点
大家对0的三角函数值非常熟悉,本节课的目的就是如何把求任意角的三角函数值问题转化为0的三角函数值问题。
实践观察
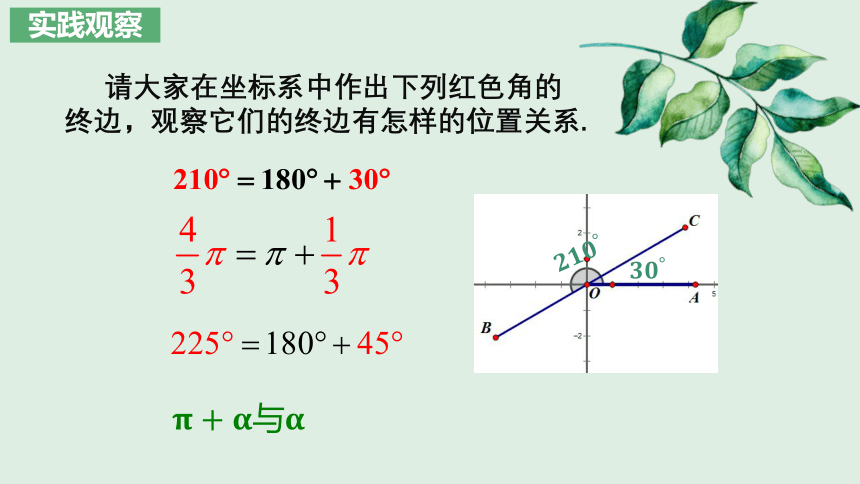
请大家在坐标系中作出下列红色角的终边,观察它们的终边有怎样的位置关系.
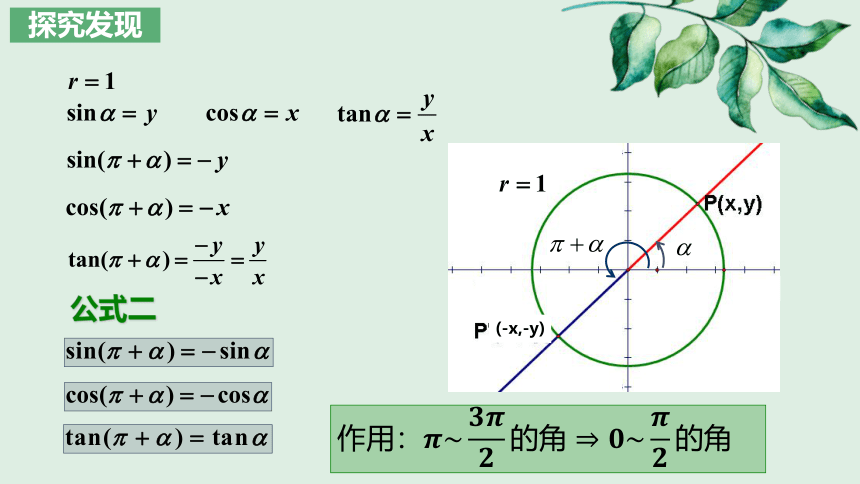
探究发现
公式二
(-x,-y)
深入探究
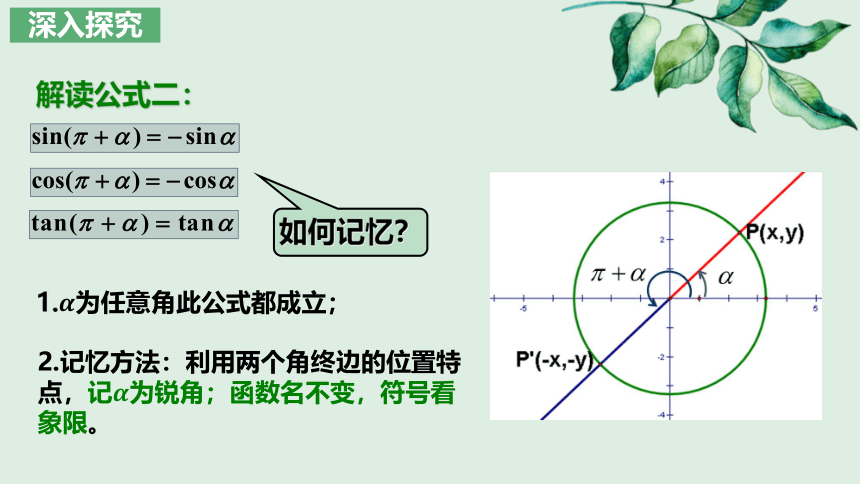
解读公式二:
1.为任意角此公式都成立;
(几何画板演示)
深入探究
解读公式二:
如何记忆?
1.为任意角此公式都成立;
2.记忆方法:利用两个角终边的位置特点,记为锐角;函数名不变,符号看象限。
探究发现
请大家用诱导公式二的方法,小组合作探究。
-
探究结果
公式三
作用:负角→正角
记忆方法:利用两个角终边的位置特点,记为锐角;函数名不变,符号看象限。
探究发现
公式四
(钝角→锐角)
记忆方法?
诱导公式二:
诱导公式三:
诱导公式四:
新知归纳
记忆方法:利用两个角终边的位置特点,记为锐角;
函数名不变,符号看象限。
新知归纳
公式二:
公式三:
公式四:
公式一:
+
探究结果
新知应用
例1.求下列三角函数值:
(1) cos225 ; (2) ; (3)
解:
(1)
cos225 = cos(180 +45 )
= -cos45
(的角的角)
新知应用
例1.求下列三角函数值:
(1) cos225 ; (2) (3)
解:
(2)
(大角化小角)
(负角化正角)
新知应用
例1.求下列三角函数值:
解:
(3)
(负角化正角)
(大角化小角)
(负角化正角)
(钝角化锐角)
(1) cos225 ; (2) (3)
任意负角的三角函数
任意正角的三角函数
0~2π的角的三角函数
锐角三角函数
归纳总结
负化正、大化小、小化锐、锐求值
根据以上解题过程,你能自己归纳一下把任意角的三角函数转化为锐角三角函数的步骤吗?
新知应用
例2. 化简
解:
= 1.
原式 =
-cos
·sin
-sin(+180 )
·cos(180 +)
sin
·(-cos)
-cos
·sin
=
练习巩固
1. 利用公式求下列三角函数值:
(1) cos(-420 ); (2)
解:
(1)
cos(-420 ) = cos420
= cos(360 +60 )
= cos60
(2)
2. 化简:sin(+180)cos(-)sin(--180).
练习巩固
解:
原式 =
-sin cos [-sin(+180 )]
= -sin cos sin
= -sin2 cos .
课堂小结
记忆方法:利用两个角终边的位置特点,
负化正、大化小、小化锐、锐求值
思想方法:
求任意角的三角函数值,方法:
记为锐角;函数名不变,符号看象限。
由未知转化为已知的化归思想
数形结合思想(单位圆与三角函数)
评价提升
课后作业
书上第27页:第2题、第3题.
探究:
的三角函数有什么关系 与呢
学而不思则罔,思而不学则殆。
5.3 三角函数的诱导公式
(第1课时)
普通高中课程标准实验教科书·人教A版2019·数学必修第一册
复习回顾
x
y
0
P(x,y)
α的终边
1
1
1.三角函数的定义:
α的正弦值等于它的终边与单位圆交点的纵坐标
简记为:在单位圆里,看y,cos看x,tan看y比x.
复习回顾
2. α+2kπ(k∈Z)与α的三角函数之间的关系是什么?
公式一:
( )
作用:将任意角转化为0到2范围内的角.
发现问题
3.你能求sin750°和sin930°的值吗?
=
本节要点
大家对0的三角函数值非常熟悉,本节课的目的就是如何把求任意角的三角函数值问题转化为0的三角函数值问题。
实践观察
请大家在坐标系中作出下列红色角的终边,观察它们的终边有怎样的位置关系.
探究发现
公式二
(-x,-y)
深入探究
解读公式二:
1.为任意角此公式都成立;
(几何画板演示)
深入探究
解读公式二:
如何记忆?
1.为任意角此公式都成立;
2.记忆方法:利用两个角终边的位置特点,记为锐角;函数名不变,符号看象限。
探究发现
请大家用诱导公式二的方法,小组合作探究。
-
探究结果
公式三
作用:负角→正角
记忆方法:利用两个角终边的位置特点,记为锐角;函数名不变,符号看象限。
探究发现
公式四
(钝角→锐角)
记忆方法?
诱导公式二:
诱导公式三:
诱导公式四:
新知归纳
记忆方法:利用两个角终边的位置特点,记为锐角;
函数名不变,符号看象限。
新知归纳
公式二:
公式三:
公式四:
公式一:
+
探究结果
新知应用
例1.求下列三角函数值:
(1) cos225 ; (2) ; (3)
解:
(1)
cos225 = cos(180 +45 )
= -cos45
(的角的角)
新知应用
例1.求下列三角函数值:
(1) cos225 ; (2) (3)
解:
(2)
(大角化小角)
(负角化正角)
新知应用
例1.求下列三角函数值:
解:
(3)
(负角化正角)
(大角化小角)
(负角化正角)
(钝角化锐角)
(1) cos225 ; (2) (3)
任意负角的三角函数
任意正角的三角函数
0~2π的角的三角函数
锐角三角函数
归纳总结
负化正、大化小、小化锐、锐求值
根据以上解题过程,你能自己归纳一下把任意角的三角函数转化为锐角三角函数的步骤吗?
新知应用
例2. 化简
解:
= 1.
原式 =
-cos
·sin
-sin(+180 )
·cos(180 +)
sin
·(-cos)
-cos
·sin
=
练习巩固
1. 利用公式求下列三角函数值:
(1) cos(-420 ); (2)
解:
(1)
cos(-420 ) = cos420
= cos(360 +60 )
= cos60
(2)
2. 化简:sin(+180)cos(-)sin(--180).
练习巩固
解:
原式 =
-sin cos [-sin(+180 )]
= -sin cos sin
= -sin2 cos .
课堂小结
记忆方法:利用两个角终边的位置特点,
负化正、大化小、小化锐、锐求值
思想方法:
求任意角的三角函数值,方法:
记为锐角;函数名不变,符号看象限。
由未知转化为已知的化归思想
数形结合思想(单位圆与三角函数)
评价提升
课后作业
书上第27页:第2题、第3题.
探究:
的三角函数有什么关系 与呢
学而不思则罔,思而不学则殆。
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
