海南实验中学2005~2006学年度第一学期初二数学(上)第六章一次函数单元测试[上学期]
文档属性
| 名称 | 海南实验中学2005~2006学年度第一学期初二数学(上)第六章一次函数单元测试[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 31.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-01-21 22:13:00 | ||
图片预览

文档简介
海南实验中学2005~2006学年度第一学期 初二数学(上)第六章一次函数 单元测试 命题人:马淑敏
一次函数单元测试试题卷
一、选择题。(共10小题,每小题3分,共30分)
1、下列各点中,在一次函数y=x-1的图象上的是( ).
A、(2,1) B、(0,1) C、(2,0) D、(2,-1)
2、下列各图中是正比例函数图象的是( ).
y y y
0 x 0 x 0 x 0 x
A B C D
3、一次函数y=k(x-k)(k<0)的图象通过( ).
A、第一、二、三象限B、第一、二、四象限C、第一、三、四象限D、第二、三、四象限
4、下列函数的图象,与y轴交点在x轴上方的是( ).
A、y=-x B、y=x-1 C、y=-2x+1 D、y=-5+3x
5、命题:(1)y=2x不是一次函数;(2)y=4-3x与x轴的交点在y轴的左侧;(3)y=kx+b,当b=0时为正比例函数;(4)y=-2x+5中,y随x的增大而减小。其中正确的命题有( ).
A、1个 B、2个 C、3个 D、4个
6、已知y与x成正比例,如果x=2时,y=1,那么x=3时,y等于( ).
A、1 B、1.5 C、2 D、6
7、一次函数y=x+b的图象与两坐标轴所围成的三角形面积为16,则b的值为( ).
A、-4 B、4 C、 4 D、4
8、一次函数的图象如图所示,其解析式应是( ).
A、 B、 y
C、 D、 0
-24
9、在同一平面直角坐标系中,小明描出了下列函数的图象:①y=-x+3;②y=x+3 ;③y=-x-3 ;④y=-3(x+1);得出的结论是:(1)过(-3,0)的是②和③;(2)两条直线相交且交于在y轴上的是③④;(3)互相平行的是①③;(4)关于x轴对称的是①②。其中说法正确的个数是( ).
A、1个 B、2个 C、3个 D、4个
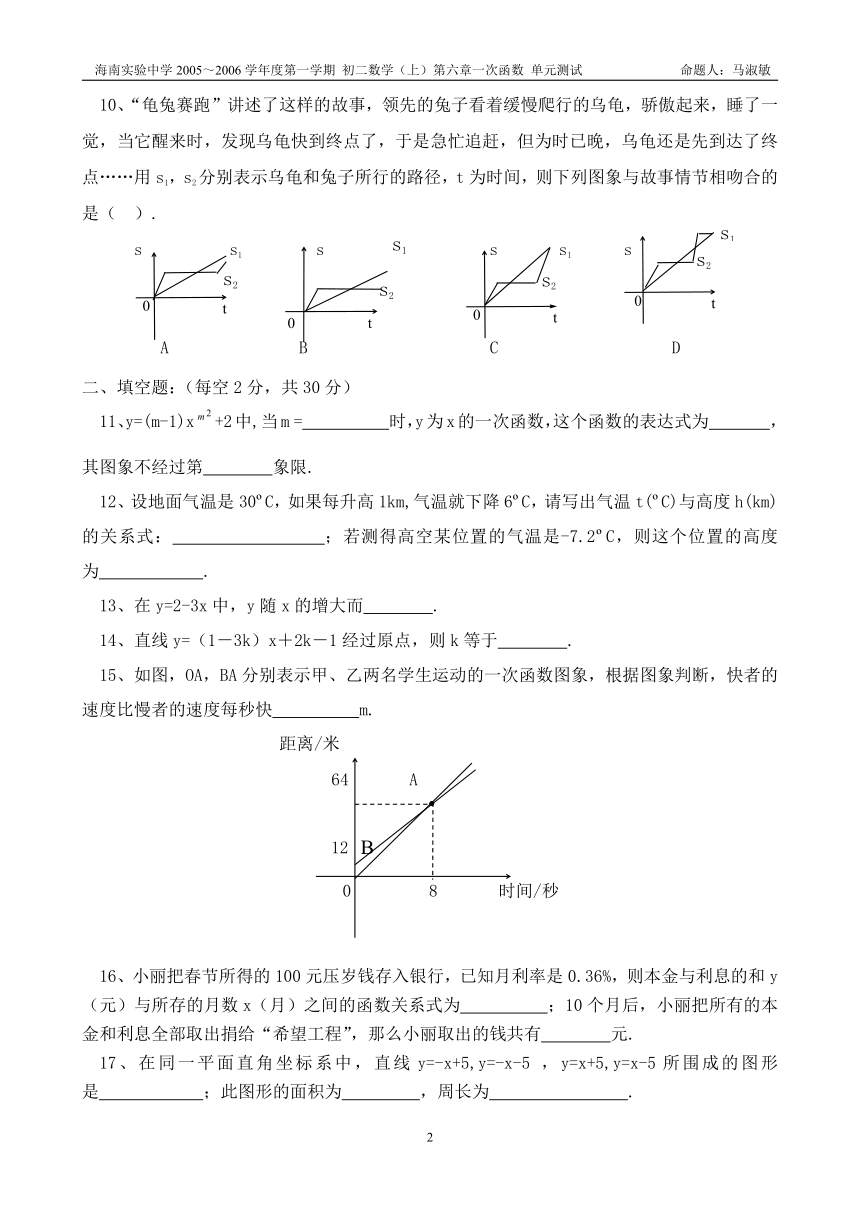
10、“龟兔赛跑”讲述了这样的故事,领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点……用s1,s2分别表示乌龟和兔子所行的路径,t为时间,则下列图象与故事情节相吻合的是( ).
s s1 s s s1 s
A B C D
二、填空题:(每空2分,共30分)
11、y=(m-1)x+2中,当m = 时,y为x的一次函数,这个函数的表达式为 ,其图象不经过第 象限.
12、设地面气温是30 C,如果每升高1km,气温就下降6 C,请写出气温t( C)与高度h(km)的关系式: ;若测得高空某位置的气温是-7.2 C,则这个位置的高度为 .
13、在y=2-3x中,y随x的增大而 .
14、直线y=(1-3k)x+2k-1经过原点,则k等于 .
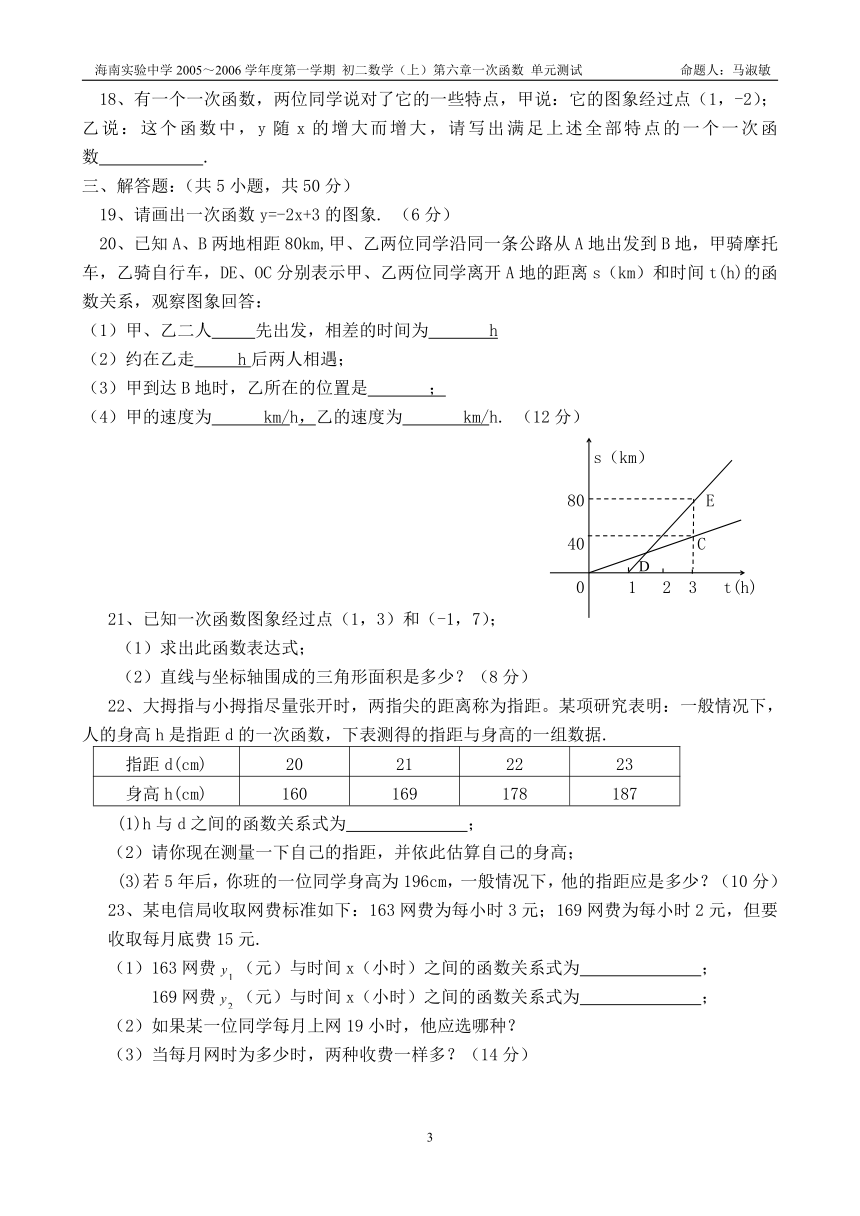
15、如图,OA,BA分别表示甲、乙两名学生运动的一次函数图象,根据图象判断,快者的速度比慢者的速度每秒快 m.
距离/米
64 A
12
0 8 时间/秒
16、小丽把春节所得的100元压岁钱存入银行,已知月利率是0.36%,则本金与利息的和y(元)与所存的月数x(月)之间的函数关系式为 ;10个月后,小丽把所有的本金和利息全部取出捐给“希望工程”,那么小丽取出的钱共有 元.
17、在同一平面直角坐标系中,直线y=-x+5,y=-x-5 ,y=x+5,y=x-5所围成的图形是 ;此图形的面积为 ,周长为 .
18、有一个一次函数,两位同学说对了它的一些特点,甲说:它的图象经过点(1,-2);乙说:这个函数中,y随x的增大而增大,请写出满足上述全部特点的一个一次函数 .
三、解答题:(共5小题,共50分)
19、请画出一次函数y=-2x+3的图象. (6分)
20、已知A、B两地相距80km,甲、乙两位同学沿同一条公路从A地出发到B地,甲骑摩托车,乙骑自行车,DE、OC分别表示甲、乙两位同学离开A地的距离s(km)和时间t(h)的函数关系,观察图象回答:
(1)甲、乙二人 先出发,相差的时间为 h
(2)约在乙走 h后两人相遇;
(3)甲到达B地时,乙所在的位置是 ;
(4)甲的速度为 km/h,乙的速度为 km/h. (12分)
s(km)
80 E
40 C
0 1 2 3 t(h)
21、已知一次函数图象经过点(1,3)和(-1,7);
(1)求出此函数表达式;
(2)直线与坐标轴围成的三角形面积是多少?(8分)
22、大拇指与小拇指尽量张开时,两指尖的距离称为指距。某项研究表明:一般情况下,人的身高h是指距d的一次函数,下表测得的指距与身高的一组数据.
指距d(cm) 20 21 22 23
身高h(cm) 160 169 178 187
(1)h与d之间的函数关系式为 ;
(2)请你现在测量一下自己的指距,并依此估算自己的身高;
(3)若5年后,你班的一位同学身高为196cm,一般情况下,他的指距应是多少?(10分)
23、某电信局收取网费标准如下:163网费为每小时3元;169网费为每小时2元,但要收取每月底费15元.
(1)163网费(元)与时间x(小时)之间的函数关系式为 ;
169网费(元)与时间x(小时)之间的函数关系式为 ;
(2)如果某一位同学每月上网19小时,他应选哪种?
(3)当每月网时为多少时,两种收费一样多?(14分)
一次函数单元测试试题题答案及评分标准
一、1C 2B 3D 4C 5A 6B 7D 8B 9C 10A
二、11、m =-1;y=-2x+2
12、t=30-6h;3.8km
13、减小; 14、0.5; 15、1.5;
16、y=100+0.36x;103.6
17、正方形;50;20√2
18、y=x-3(不唯一)
三、19、略
20、(1)乙;1; 4分
(2)1.5 6分
(3)距B地40km(或距A地40km) 8分
(4)40; 12分
21、解:(1)设此一次函数表达式为y=kx+b(k≠0) 1分
则根据题意得 3分
解得k=-2,b=5
∴此一次函数表达式为y=-2x+5 5分
(2)设直线y=-2x+5与y轴、x轴的交点分别为A、B
令x=0,y=5 ∴A的坐标为(0,5)
令y=0,x= ∴B的坐标为(,0) 7分
∴S△AOB=OA×OB=×5×= 8分
22、解:(1)h=9d-20 2分
(2)不唯一。例:某同学的指距为20.5cm 4分
那么当d=2.05时,h=9×20.5-20=164.5
∴此同学的身高约为164.5cm 6分
(3)当h=196时,9d-20=196 8分
解得d=24
∴一般情况下,他的指距应是24cm 10分
23、解:(1)=3, 2分
=2+15 4分
(2)当x=19时,=3×19=57 6分
=2×19+15=53 8分
∵>
∴应选169网 10分
(3)根据题意得3x=2x+15 12分
解得x=15
∴当每月网时为15时,两种收费一样多 14分
一次函数单元测试题评价
海南实验中学 马淑敏
一、整份测试题能较好地体现课程标准对本章内容的要求,覆盖了所有的知识面。
1、结合具体情境体会一次函数的意义。如:第10题、第12题、第20题;
2、理解一次函数和正比例函数。如:第1题、第6题、第11题、第14题;
3、会画一次函数的图象。如:第2题、第4题、第7题、第8题、第17题、第19题;
4、根据已知条件确定一次函数表达式。如:第16题、第18题、第21题、第22题、第23题;
5、根据一次函数的图象和解析式探索并理解其性质。如:第3题、第5题、第9题、第13题、第15题、第18题;
6、能用一次函数解决实际问题。如:第22题、第23题.
注:在《课程标准》里,对一次函数还有一个要求是:能根据一次函数的图象求二元一次方程组的近似解。但是在北师大版的教材中,二元一次方程组的内容是在一次函数的内容之后,因此,在本单元的测试中并未考查此项内容。
二、试题的命题特点分析:
1、注重对学生良好品质和公民数学素养的培养。
如:第10题,借助“龟兔赛跑”的故事对学生进行“不骄傲”“不偷懒”“持之以恒”等良好品质的教育;第16题与“希望工程”有关,对学生进行“爱心”教育。对一些题目的表述很注意用词,如第22题中的“请你”等,让学生感到很亲切。
2、注重与实际生活和学生的实际生活相联系。
如:第22题是一道与学生有关的身高和指距的关系的问题,会给学生一种惊奇,激发他们解题的兴趣,“寓学于乐”;第23题是与学生上网交费有关的题目,通过对问题的解决,可以使他们能主动地、自觉地对自己身边的事情做出较好的选择,从而优化自己的生活;第16题是有关学生经常会遇到的“压岁钱”的问题。
3、注重思想方法的渗透。
(1)数形结合思想:如第7题、第9题、第15题、第17题、第20题。这些题目都有助于培养学生将数和形结合起来解决问题。
(2)函数与方程思想:如第12题、第14题、第16题、第22题、第23题。这些题目都有助于让学生感受到:利用函数与方程思想解决实际问题的方便和有效。
(3)特殊化与一般化思想:如第22(1)题,学生可以从表格中的数据(特例)归纳出h与d之间的函数关系式(一般化),培养学生的观察能力和归纳能力。
4、注重知识间的综合。
如:第17题与几何图形求面积和周长相联系,求面积时,学生可以用正方形面积去求,也可以用四个小三角形的面积和或两个大三角形面积和去求,还可以用对角线乘积的一半去求等,体现了方法的多样性;求周长时,还用到了勾股定理;第9题与两直线的位置关系及图形的对称性等相联系。这些都有效地加强了知识间的联系。
5、能体现时代特色。
如:第16题与“希望工程”联系,第23题与学生上网交费有关;
6、注重对所选旧题的改编。如:
第22题原题是这样的:“(1)求出h与d之间的函数关系式;(2)若5年后,你班的一位同学身高为196cm,一般情况下,他的指距应是多少?”。我将之改为“(1)h与d之间的函数关系式为 ;(2)请你现在测量一下自己的指距,并依此估算自己的身高;(3)若5年后,你班的一位同学身高为196cm,一般情况下,他的指距应是多少?”。这样改后,学生在做第(1)问时,可以不局限于用观察规律的方法或用待定系数法去求;加上了第(2)问,增强了题目的趣味性,也让学生感觉到亲切。
第23题由原来的“(1)你能写出网费y(元)与时间x(小时)的函数关系式吗?”改为“(1)163网费y(元)与时间x(小时)之间的函数关系式为 ;169网费y(元)与时间x(小时)之间的函数关系式为 ;”。这样改后,学生比较节省答题的时间,提高解题的效率。
第21题将“(2)写出直线与x轴,y轴交点的坐标;(3)直线与坐标轴围成的三角形面积是多少?(4)y随x的变化情况如何?”改为“(2)直线与坐标轴围成的三角形面积是多少?”,去掉了第(4)小问,并将第(2)小问融入第(3)小问之中,使表达更为简练。
第20题由原来的解答题“(1)甲、乙谁先出发?谁后出发 ?相差多长时间?(2)约在乙走多长时间后两人相遇?相遇点离A地多远?(3)甲到达B地时,乙在何处?(4)求甲、乙两人骑车速度。”改为填空题“(1)甲、乙二人 先出发,相差的时间为 h(2)约在乙走 h后两人相遇;(3)甲到达B地时,乙所在的位置是 ;(4)甲的速度为 km/h,乙的速度为 km/h.”,使表述和解答更为简练,节省了学生不必要浪费的时间;也减轻了评卷的工作量。
7、关注题目的开放性。
如:第18题
总之,这份测试题能够较好地体现新课程标准的要求,能够紧扣教材,根据学生的实际情况进行命题,是一份适合我们的学生的单元测试题。
6
0
s2
0
t
s2
s1 s1s1
y
D
B
t
t
t
s2
0
s1
s2
0
PAGE
5
一次函数单元测试试题卷
一、选择题。(共10小题,每小题3分,共30分)
1、下列各点中,在一次函数y=x-1的图象上的是( ).
A、(2,1) B、(0,1) C、(2,0) D、(2,-1)
2、下列各图中是正比例函数图象的是( ).
y y y
0 x 0 x 0 x 0 x
A B C D
3、一次函数y=k(x-k)(k<0)的图象通过( ).
A、第一、二、三象限B、第一、二、四象限C、第一、三、四象限D、第二、三、四象限
4、下列函数的图象,与y轴交点在x轴上方的是( ).
A、y=-x B、y=x-1 C、y=-2x+1 D、y=-5+3x
5、命题:(1)y=2x不是一次函数;(2)y=4-3x与x轴的交点在y轴的左侧;(3)y=kx+b,当b=0时为正比例函数;(4)y=-2x+5中,y随x的增大而减小。其中正确的命题有( ).
A、1个 B、2个 C、3个 D、4个
6、已知y与x成正比例,如果x=2时,y=1,那么x=3时,y等于( ).
A、1 B、1.5 C、2 D、6
7、一次函数y=x+b的图象与两坐标轴所围成的三角形面积为16,则b的值为( ).
A、-4 B、4 C、 4 D、4
8、一次函数的图象如图所示,其解析式应是( ).
A、 B、 y
C、 D、 0
-24
9、在同一平面直角坐标系中,小明描出了下列函数的图象:①y=-x+3;②y=x+3 ;③y=-x-3 ;④y=-3(x+1);得出的结论是:(1)过(-3,0)的是②和③;(2)两条直线相交且交于在y轴上的是③④;(3)互相平行的是①③;(4)关于x轴对称的是①②。其中说法正确的个数是( ).
A、1个 B、2个 C、3个 D、4个
10、“龟兔赛跑”讲述了这样的故事,领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点……用s1,s2分别表示乌龟和兔子所行的路径,t为时间,则下列图象与故事情节相吻合的是( ).
s s1 s s s1 s
A B C D
二、填空题:(每空2分,共30分)
11、y=(m-1)x+2中,当m = 时,y为x的一次函数,这个函数的表达式为 ,其图象不经过第 象限.
12、设地面气温是30 C,如果每升高1km,气温就下降6 C,请写出气温t( C)与高度h(km)的关系式: ;若测得高空某位置的气温是-7.2 C,则这个位置的高度为 .
13、在y=2-3x中,y随x的增大而 .
14、直线y=(1-3k)x+2k-1经过原点,则k等于 .
15、如图,OA,BA分别表示甲、乙两名学生运动的一次函数图象,根据图象判断,快者的速度比慢者的速度每秒快 m.
距离/米
64 A
12
0 8 时间/秒
16、小丽把春节所得的100元压岁钱存入银行,已知月利率是0.36%,则本金与利息的和y(元)与所存的月数x(月)之间的函数关系式为 ;10个月后,小丽把所有的本金和利息全部取出捐给“希望工程”,那么小丽取出的钱共有 元.
17、在同一平面直角坐标系中,直线y=-x+5,y=-x-5 ,y=x+5,y=x-5所围成的图形是 ;此图形的面积为 ,周长为 .
18、有一个一次函数,两位同学说对了它的一些特点,甲说:它的图象经过点(1,-2);乙说:这个函数中,y随x的增大而增大,请写出满足上述全部特点的一个一次函数 .
三、解答题:(共5小题,共50分)
19、请画出一次函数y=-2x+3的图象. (6分)
20、已知A、B两地相距80km,甲、乙两位同学沿同一条公路从A地出发到B地,甲骑摩托车,乙骑自行车,DE、OC分别表示甲、乙两位同学离开A地的距离s(km)和时间t(h)的函数关系,观察图象回答:
(1)甲、乙二人 先出发,相差的时间为 h
(2)约在乙走 h后两人相遇;
(3)甲到达B地时,乙所在的位置是 ;
(4)甲的速度为 km/h,乙的速度为 km/h. (12分)
s(km)
80 E
40 C
0 1 2 3 t(h)
21、已知一次函数图象经过点(1,3)和(-1,7);
(1)求出此函数表达式;
(2)直线与坐标轴围成的三角形面积是多少?(8分)
22、大拇指与小拇指尽量张开时,两指尖的距离称为指距。某项研究表明:一般情况下,人的身高h是指距d的一次函数,下表测得的指距与身高的一组数据.
指距d(cm) 20 21 22 23
身高h(cm) 160 169 178 187
(1)h与d之间的函数关系式为 ;
(2)请你现在测量一下自己的指距,并依此估算自己的身高;
(3)若5年后,你班的一位同学身高为196cm,一般情况下,他的指距应是多少?(10分)
23、某电信局收取网费标准如下:163网费为每小时3元;169网费为每小时2元,但要收取每月底费15元.
(1)163网费(元)与时间x(小时)之间的函数关系式为 ;
169网费(元)与时间x(小时)之间的函数关系式为 ;
(2)如果某一位同学每月上网19小时,他应选哪种?
(3)当每月网时为多少时,两种收费一样多?(14分)
一次函数单元测试试题题答案及评分标准
一、1C 2B 3D 4C 5A 6B 7D 8B 9C 10A
二、11、m =-1;y=-2x+2
12、t=30-6h;3.8km
13、减小; 14、0.5; 15、1.5;
16、y=100+0.36x;103.6
17、正方形;50;20√2
18、y=x-3(不唯一)
三、19、略
20、(1)乙;1; 4分
(2)1.5 6分
(3)距B地40km(或距A地40km) 8分
(4)40; 12分
21、解:(1)设此一次函数表达式为y=kx+b(k≠0) 1分
则根据题意得 3分
解得k=-2,b=5
∴此一次函数表达式为y=-2x+5 5分
(2)设直线y=-2x+5与y轴、x轴的交点分别为A、B
令x=0,y=5 ∴A的坐标为(0,5)
令y=0,x= ∴B的坐标为(,0) 7分
∴S△AOB=OA×OB=×5×= 8分
22、解:(1)h=9d-20 2分
(2)不唯一。例:某同学的指距为20.5cm 4分
那么当d=2.05时,h=9×20.5-20=164.5
∴此同学的身高约为164.5cm 6分
(3)当h=196时,9d-20=196 8分
解得d=24
∴一般情况下,他的指距应是24cm 10分
23、解:(1)=3, 2分
=2+15 4分
(2)当x=19时,=3×19=57 6分
=2×19+15=53 8分
∵>
∴应选169网 10分
(3)根据题意得3x=2x+15 12分
解得x=15
∴当每月网时为15时,两种收费一样多 14分
一次函数单元测试题评价
海南实验中学 马淑敏
一、整份测试题能较好地体现课程标准对本章内容的要求,覆盖了所有的知识面。
1、结合具体情境体会一次函数的意义。如:第10题、第12题、第20题;
2、理解一次函数和正比例函数。如:第1题、第6题、第11题、第14题;
3、会画一次函数的图象。如:第2题、第4题、第7题、第8题、第17题、第19题;
4、根据已知条件确定一次函数表达式。如:第16题、第18题、第21题、第22题、第23题;
5、根据一次函数的图象和解析式探索并理解其性质。如:第3题、第5题、第9题、第13题、第15题、第18题;
6、能用一次函数解决实际问题。如:第22题、第23题.
注:在《课程标准》里,对一次函数还有一个要求是:能根据一次函数的图象求二元一次方程组的近似解。但是在北师大版的教材中,二元一次方程组的内容是在一次函数的内容之后,因此,在本单元的测试中并未考查此项内容。
二、试题的命题特点分析:
1、注重对学生良好品质和公民数学素养的培养。
如:第10题,借助“龟兔赛跑”的故事对学生进行“不骄傲”“不偷懒”“持之以恒”等良好品质的教育;第16题与“希望工程”有关,对学生进行“爱心”教育。对一些题目的表述很注意用词,如第22题中的“请你”等,让学生感到很亲切。
2、注重与实际生活和学生的实际生活相联系。
如:第22题是一道与学生有关的身高和指距的关系的问题,会给学生一种惊奇,激发他们解题的兴趣,“寓学于乐”;第23题是与学生上网交费有关的题目,通过对问题的解决,可以使他们能主动地、自觉地对自己身边的事情做出较好的选择,从而优化自己的生活;第16题是有关学生经常会遇到的“压岁钱”的问题。
3、注重思想方法的渗透。
(1)数形结合思想:如第7题、第9题、第15题、第17题、第20题。这些题目都有助于培养学生将数和形结合起来解决问题。
(2)函数与方程思想:如第12题、第14题、第16题、第22题、第23题。这些题目都有助于让学生感受到:利用函数与方程思想解决实际问题的方便和有效。
(3)特殊化与一般化思想:如第22(1)题,学生可以从表格中的数据(特例)归纳出h与d之间的函数关系式(一般化),培养学生的观察能力和归纳能力。
4、注重知识间的综合。
如:第17题与几何图形求面积和周长相联系,求面积时,学生可以用正方形面积去求,也可以用四个小三角形的面积和或两个大三角形面积和去求,还可以用对角线乘积的一半去求等,体现了方法的多样性;求周长时,还用到了勾股定理;第9题与两直线的位置关系及图形的对称性等相联系。这些都有效地加强了知识间的联系。
5、能体现时代特色。
如:第16题与“希望工程”联系,第23题与学生上网交费有关;
6、注重对所选旧题的改编。如:
第22题原题是这样的:“(1)求出h与d之间的函数关系式;(2)若5年后,你班的一位同学身高为196cm,一般情况下,他的指距应是多少?”。我将之改为“(1)h与d之间的函数关系式为 ;(2)请你现在测量一下自己的指距,并依此估算自己的身高;(3)若5年后,你班的一位同学身高为196cm,一般情况下,他的指距应是多少?”。这样改后,学生在做第(1)问时,可以不局限于用观察规律的方法或用待定系数法去求;加上了第(2)问,增强了题目的趣味性,也让学生感觉到亲切。
第23题由原来的“(1)你能写出网费y(元)与时间x(小时)的函数关系式吗?”改为“(1)163网费y(元)与时间x(小时)之间的函数关系式为 ;169网费y(元)与时间x(小时)之间的函数关系式为 ;”。这样改后,学生比较节省答题的时间,提高解题的效率。
第21题将“(2)写出直线与x轴,y轴交点的坐标;(3)直线与坐标轴围成的三角形面积是多少?(4)y随x的变化情况如何?”改为“(2)直线与坐标轴围成的三角形面积是多少?”,去掉了第(4)小问,并将第(2)小问融入第(3)小问之中,使表达更为简练。
第20题由原来的解答题“(1)甲、乙谁先出发?谁后出发 ?相差多长时间?(2)约在乙走多长时间后两人相遇?相遇点离A地多远?(3)甲到达B地时,乙在何处?(4)求甲、乙两人骑车速度。”改为填空题“(1)甲、乙二人 先出发,相差的时间为 h(2)约在乙走 h后两人相遇;(3)甲到达B地时,乙所在的位置是 ;(4)甲的速度为 km/h,乙的速度为 km/h.”,使表述和解答更为简练,节省了学生不必要浪费的时间;也减轻了评卷的工作量。
7、关注题目的开放性。
如:第18题
总之,这份测试题能够较好地体现新课程标准的要求,能够紧扣教材,根据学生的实际情况进行命题,是一份适合我们的学生的单元测试题。
6
0
s2
0
t
s2
s1 s1s1
y
D
B
t
t
t
s2
0
s1
s2
0
PAGE
5
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
