【精选备课】2022年秋青岛版初中数学九年级上册 期中复习与测试(含解析)
文档属性
| 名称 | 【精选备课】2022年秋青岛版初中数学九年级上册 期中复习与测试(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 928.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 17:51:37 | ||
图片预览



文档简介
期中复习与测试
一、单选题
1.如图,在△ABC中,点G为△ABC的重心,过点G作DE∥BC,分别交AB、AC于点D、E,则△ADE与四边形DBCE的面积比为( )
A. B. C. D.
2.如果,那么的结果是( )
A. B. C. D.
3.在中,,则的值是( ).
A. B. C. D.
4.如图,菱形 ABCD 的边长为4 ,A 60, M 是 AD 的中点, N 是 AB 边上一动点, 将AMN 沿 MN 所在的直线翻折得到AMN ,连接 AC ,则当 AC 取得最小值时, tan DCA的值为( )
A. B. C. D.
5.如图,小明在一条东西走向公路的O处,测得图书馆A在他的北偏东方向,且与他相距,则图书馆A到公路的距离为( )
A. B. C. D.
6.在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角形△ADE(不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形△ADE只算一个),这样的格点三角形一共有( )
A.4个 B.5个 C.6个 D.7个
7.若为锐角,,则等于( )
A. B. C. D.
8.如图,AD//BC,∠D=90°,AD=3,BC=4,DC=6,若在边 DC上有点P,使△PAD 与△PBC相似,则这样的点 P 有( )
A.1 个 B.2 个 C.3 个 D.4 个
9.如图,将一张宽为2cm的长方形纸片沿AB折叠成如图所示的形状,那么折痕AB的长为( )cm
A. B. C.2 D.
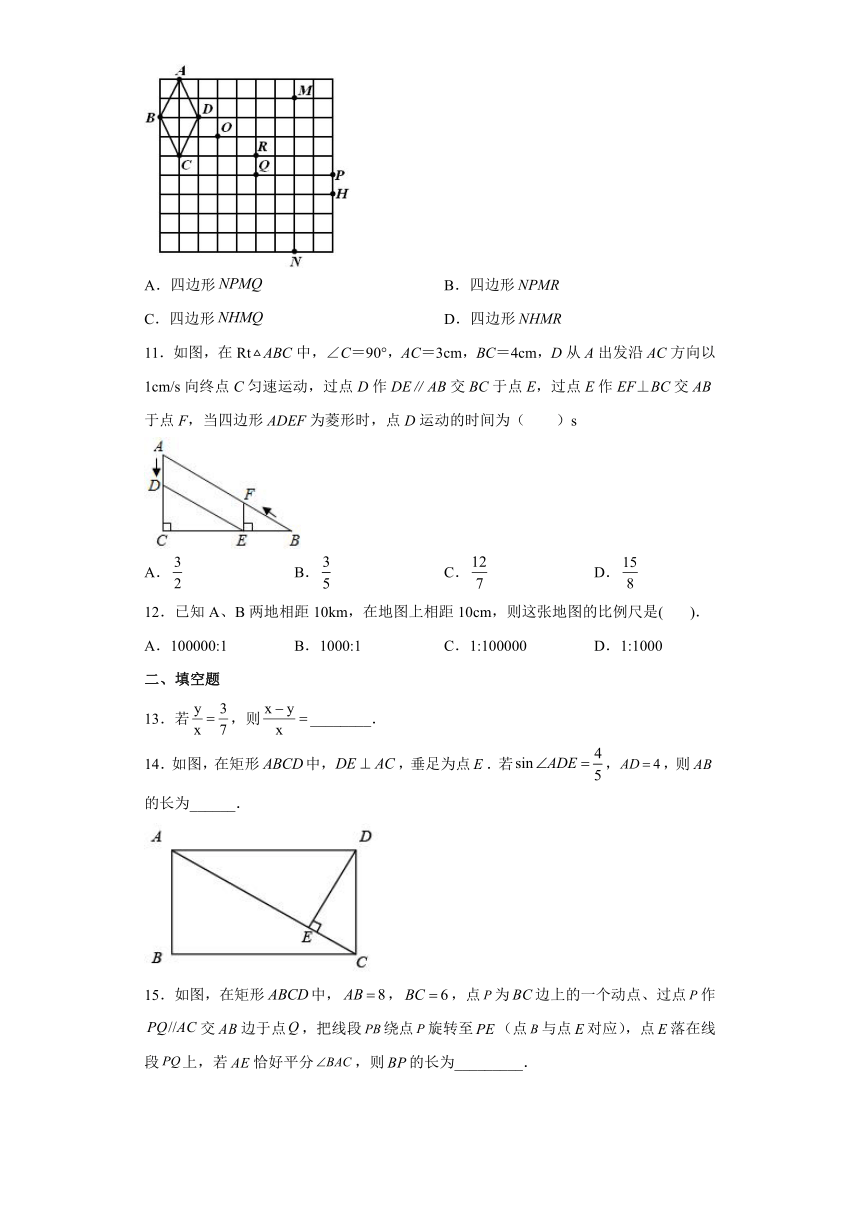
10.在如图所示的网格中,以点为位似中心,四边形的位似图形是( )
A.四边形 B.四边形
C.四边形 D.四边形
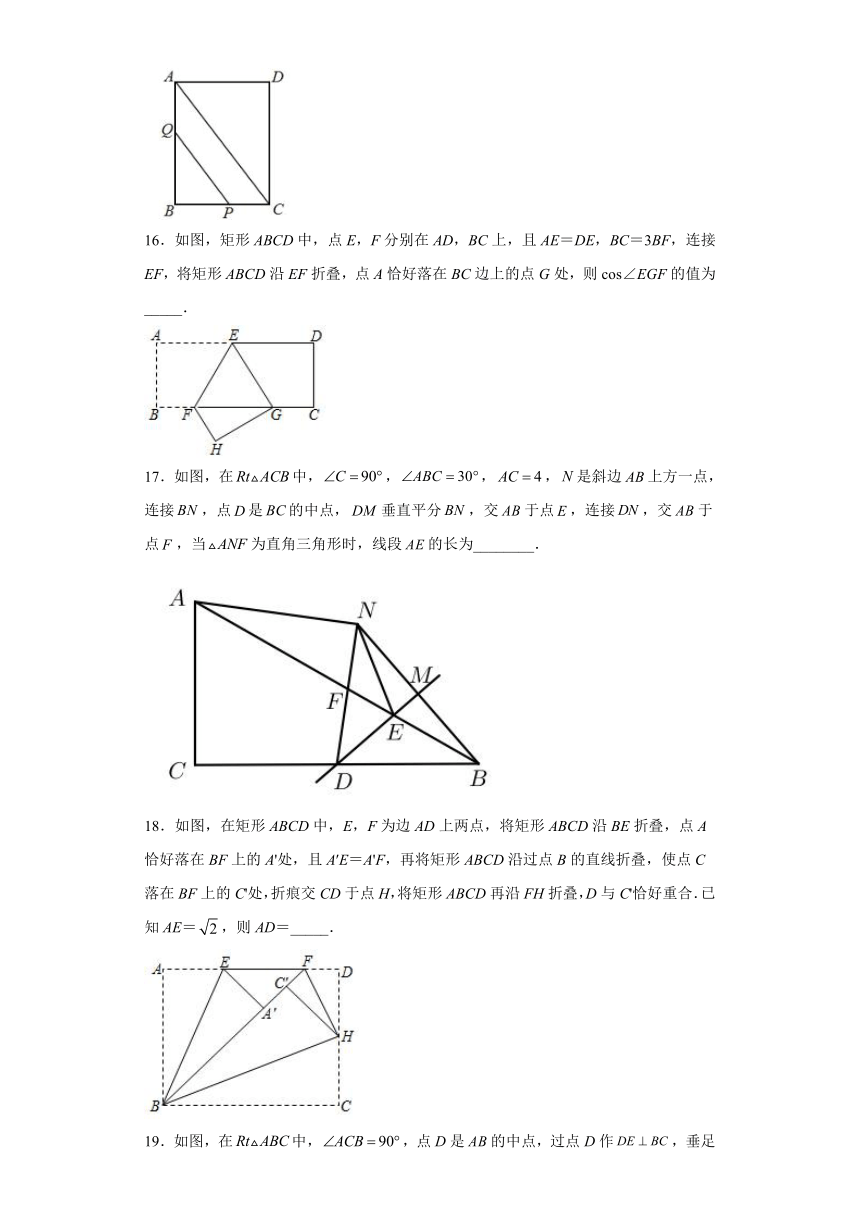
11.如图,在RtABC中,∠C=90°,AC=3cm,BC=4cm,D从A出发沿AC方向以1cm/s向终点C匀速运动,过点D作DEAB交BC于点E,过点E作EF⊥BC交AB于点F,当四边形ADEF为菱形时,点D运动的时间为( )s
A. B. C. D.
12.已知A、B两地相距10km,在地图上相距10cm,则这张地图的比例尺是( ).
A.100000:1 B.1000:1 C.1:100000 D.1:1000
二、填空题
13.若,则________.
14.如图,在矩形中,,垂足为点.若,,则的长为______.
15.如图,在矩形中,,,点为边上的一个动点、过点作交边于点,把线段绕点旋转至(点与点对应),点落在线段上,若恰好平分,则的长为_________.
16.如图,矩形ABCD中,点E,F分别在AD,BC上,且AE=DE,BC=3BF,连接EF,将矩形ABCD沿EF折叠,点A恰好落在BC边上的点G处,则cos∠EGF的值为_____.
17.如图,在中,,,,是斜边上方一点,连接,点是的中点,垂直平分,交于点,连接,交于点,当为直角三角形时,线段的长为________.
18.如图,在矩形ABCD中,E,F为边AD上两点,将矩形ABCD沿BE折叠,点A恰好落在BF上的A'处,且A′E=A'F,再将矩形ABCD沿过点B的直线折叠,使点C落在BF上的C'处,折痕交CD于点H,将矩形ABCD再沿FH折叠,D与C'恰好重合.已知AE=,则AD=_____.
19.如图,在中,,点D是的中点,过点D作,垂足为点E,连接,若,,则________.
三、解答题
20.为了测量大楼顶上(居中)避雷针BC的长度,在地面上点A处测得避雷针底部B和顶部C的仰角分别为55°58′和57°,已知点A与楼底中间部位D的距离约为80米,求避雷针BC的长度.(参考数据:sin55°58′≈0.83,cos55°58′≈0.56,tan55°58′≈1.48,sin57°≈0.84,tan57°≈1.54)
21.五一期间,小明跟父母去乌镇旅游,欣赏乌镇水乡的美景.如图,当小明走到乌镇古桥的C处时,发现远处有一瞍船匀速行驶过来,当船行驶到A处时,小明测得船头的俯角为30°,同时小明开始计时,船在航行过小明所在的桥之后,继续向前航行到达B处,此时测得船尾的俯角为45°;从小明开始计时到船行驶至B处,共用时15min;已知小明所在位置距离水面6m,船长3m,船到水面的距离忽略不计,请你帮助小明计算一下船的航行速度(结果保留根号)
22.如图,在的正三角形的网格中,的三个顶点都在格点上.请按要求画图和计算:①仅用无刻度直尺;②保留作图痕迹.
(1)在图1中,画出的边上的中线.
(2)在图2中,求的值.
23.新冠肺炎疫情期间,我国各地采取了多种方式进行预防.其中,某地运用无人机规劝居民回家.如图,无人机于空中A处测得某建筑顶部B处的仰角为,测得该建筑底部C处的俯角为.若无人机的飞行高度为,求该建筑的高度(结果取整数),参考数据:,,.
24.如图1,某同学家的一面窗户上安装有遮阳篷,图2和图3是截面示意图,CD是遮阳篷,窗户AB为1.5米,BC为0.5米.该遮阳篷有伸缩功能.如图2,该同学在夏季某日的正午时刻测得太阳光和水平线的夹角为60°,遮阳篷CD正好将进入窗户AB的阳光挡住;如图3,该同学在冬季某日的正午时刻测得太阳光和水平线的夹角为30°,将遮阳篷收缩成CD′时,遮阳篷正好完全不挡进入窗户AB的阳光.
(1)计算图3中CD′的长度比图2中CD的长度收缩了多少米;(结果保留根号)
(2)如果图3中遮阳篷的长度为图2中CD的长度,请计算该遮阳篷落在窗户AB上的阴影长度为多少米?(请在图3中画图并标出相应字母,然后再计算)
25.如图,在边长为1的正方形网格中建立平面直角坐标系,已知△ABC三个顶点分别为A(﹣1,2)、B(2,1)、C(4,5).
(1)以原点O为位似中心,在x轴的上方画出△A1B1C1,使△A1B1C1与△ABC位似,且相似比为2;
(2)△A1B1C1的面积是 平方单位.
(3)点P(a,b)为△ABC内一点,则在△A1B1C1内的对应点P’的坐标为 .
参考答案:
1.A
【解析】
【分析】
连接AG并延长交BC于H,如图,利用三角形重心的性质得到AG=2GH,再证明△ADE∽△ABC,根据相似三角形的性质得到==,然后根据比例的性质得到△ADE与四边形DBCE的面积比.
【详解】
解:连接AG并延长交BC于H,如图,
∵点G为△ABC的重心,
∴AG=2GH,
∴=,
∵DE∥BC,
∴△ADE∽△ABC,
∴==()2=,
∴△ADE与四边形DBCE的面积比=.
故选:A.
【点睛】
本题考查了三角形的重心与相似三角形的性质与判定. 重心到顶点的距离与重心到对边中点的距离之比为2∶1.
2.B
【解析】
【分析】
根据比例的性质即可得到结论.
【详解】
∵=,
∴可设a=2k,b=3k,
∴==-.
故选B.
【点睛】
本题主要考查了比例的性质,解本题的要点根据题意可设a,b的值,从而求出答案.
3.C
【解析】
【分析】
首先根据勾股定理求得AC的长,然后根据正弦的定义即可求解.
【详解】
解:根据勾股定理可得:AC==,
∴sinB==.
故选:C.
【点睛】
本题主要考查了求一个角的正弦值,求出AC的长,正确理解正弦的定义是解题关键.
4.B
【解析】
【分析】
首先根据两点之间线段最短确定点的位置,再作MH⊥DC,然后根据菱形的性质可知MD,∠HDM,再根据30°直角三角形的性质求出HD和HM,进而求出CH,最后根据正切值定义求出答案即可.
【详解】
因为是定值,两点之间线段最短,即当点在MC上时,取最小值.
过点M作MH⊥DC于点H.
边长为4的菱形ABCD中,∠A=60°,
∵M为AD的中点,
∴2MD=AD=CD=4,∠HDM=60°,
∴∠MDH=∠HDM=60°,
∴∠HMD=30°,
∴,
∴,
∴CH=HD+CD=5,
∴,
∴的值为.
故选:B.
【点睛】
这是一道应用菱形的性质求线段最短问题,主要考查了菱形的性质,翻折的性质,锐角三角函数,直角三角形的性质等.
5.A
【解析】
【分析】
根据题意可得△OAB为直角三角形,∠AOB=30°,OA=200m,根据三角函数定义即可求得AB的长.
【详解】
解:由已知得,∠AOB=90°60°=30°,OA=200m.
则AB=OA=100m.
故选:A.
【点睛】
本题主要考查了解直角三角形的应用——方向角问题,正确记忆三角函数的定义是解决本题的关键.
6.C
【解析】
【分析】
根据题意,得出ABC的三边之比,并在直角坐标系中找出与ABC各边长成比例的相似三角形,并在直角坐标系中无一遗漏地表示出来.
【详解】
解:ABC的三边之比为,
如图所示,可能出现的相似三角形共有以下六种情况:
所以使得△ADE∽△ABC的格点三角形一共有6个,
故选:C.
【点睛】
本题考察了在直角坐标系中画出与已知三角形相似的图形,解题的关键在于找出与已知三角形各边长成比例的三角形,并在直角坐标系中无一遗漏地表示出来.
7.B
【解析】
【分析】
根据tan45°=1求出即可.
【详解】
∵∠A为锐角,tanA=1,∴∠A=45°.
故选B.
【点睛】
本题考查了特殊角的三角函数值,主要考查学生的记忆能力和计算能力.
8.A
【解析】
【分析】
根据已知分两种情况△PAD∽△PBC或△PAD∽△CBP来进行分析,求得PD的长,从而确定P存在的个数.
【详解】
解:∵AD∥BC,∠D=90°,
∴∠C=∠D=90°,
∵DC=6,AD=3,BC=4,
设PD=x,则PC=6-x.
①若PD:PC=AD:BC,则△PAD∽△PBC,
则,
解得:x=,
经检验:x=是原方程的解;
②若PD:BC=AD:PC,则△PAD∽△BPC,
则,
解得:x无解,
所以这样的点P存在的个数有1个.
故选:A.
【点睛】
此题考查了相似三角形的性质,熟练掌握相似三角形对应边成比例是解本题的关键.
9.A
【解析】
【分析】
作点A作,交BC于点D,作点B作,交AC于点E,根据长方形纸条的宽得出,继而可证明是等边三角形,则有,然后在直角三角形中利用锐角三角函数即可求出AB的值.
【详解】
作点A作,交BC于点D,作点B作,交AC于点E,
∵长方形的宽为2cm,
,
,
.
∴是等边三角形,
故选:A.
【点睛】
本题主要考查等边三角形的判定及性质,锐角三角函数,掌握等边三角形的判定及性质和特殊角的三角函数值是解题的关键.
10.A
【解析】
【分析】
以O为位似中心,作四边形ABCD的位似图形,根据图像可判断出答案.
【详解】
解:如图所示,四边形的位似图形是四边形.
故选:A
【点睛】
此题考查了位似图形的作法,画位似图形的一般步骤为:①确定位似中心;②分别连接并延长位似中心和能代表原图的关键点;③根据相似比,确定能代表所作的位似图形的关键点;顺次连接上述各点,确定位似图形.
11.D
【解析】
【分析】
由勾股定理可求AB的长,由锐角三角函数可得 ,即可求解.
【详解】
解:设经过t秒后,四边形ADEF是菱形,
∴AD=DE=t,DE∥AB,
∴CD=(3-t)(cm),∠ABC=∠DEC,
∵∠C=90°,AC=3cm,BC=4cm,
∴ (cm),
∵sin∠DEC=sin∠ABC=,
∴ ,
∴ ,
故选:D.
【点睛】
本题考查了菱形的性质,勾股定理,锐角三角函数等知识,灵活运用这些性质解决问题是本题的关键.
12.C
【解析】
【分析】
比例尺=图上距离:实际距离,根据题意可直接求得比例尺.
【详解】
∵10km=1000000cm,
∴比例尺为10:1000000=1:100000.
故选C.
【点睛】
掌握比例尺的计算方法,注意在求比的过程中,单位要统一.比例尺=图上距离:实际距离,图上距离在前,实际距离在后.
13.
【解析】
【分析】
设,,代入求解即可.
【详解】
由可设,,k是非零整数,
则.
故答案为:.
【点睛】
本题主要考查了比例的基本性质,准确利用性质变形是解题的关键.
14.3
【解析】
【分析】
在中,由正弦定义解得,再由勾股定理解得DE的长,根据同角的余角相等,得到,最后根据正弦定义解得CD的长即可解题.
【详解】
解:在中,
在矩形中,
故答案为:3.
【点睛】
本题考查矩形的性质、正弦、勾股定理等知识,是重要考点,难度较易,掌握相关知识是解题关键.
15.4
【解析】
【分析】
因为PQ∥AC,可得tan∠QPB=tan∠ACB=,设QB=4x,BP=3x,则QP=5x,PE=PB=3x,QE=5x 3x=2x,因为AE恰好平分∠BAC,可得∠CAE=∠QAE=∠QEA,所以AQ=QE=2x,AB=AQ+QB=2x+4x=6x=8,解得x的值,即可得出BP的长.
【详解】
解:如图,
∵在矩形ABCD中,AB=8,BC=6,
∴tan∠ACB==,
∵PQ∥AC,
∴∠QPB=∠ACB,
∴tan∠QPB=tan∠ACB=,
设QB=4x,BP=3x,
则QP=5x,
∵把线段PB绕点P旋转至PE(点B与点E对应),点E落在线段PQ上,
∴PE=PB=3x,QE=5x 3x=2x,
∵AE恰好平分∠BAC,
∴∠CAE=∠QAE,
∵PQ∥AC,
∴∠QEA=∠CAE,
∴∠QEA=∠QAE,
∴AQ=QE=2x,
∴AB=AQ+QB=2x+4x=6x=8,
∴BP=3x=4.
故答案为:4.
【点睛】
本题考查图形旋转的性质,锐角三角函数的定义,平行线的性质和角平分线的定义,等腰三角形的判定.解题的关键是掌握图形旋转的性质.
16.
【解析】
【分析】
连接AF,由矩形的性质得AD∥BC,AD=BC,由平行线的性质得∠AEF=∠GFE,由折叠的性质得∠AFE=∠GFE,AF=FG,推出∠AEF=∠AFE,则AF=AE,AE=FG,得出四边形AFGE是菱形,则AF∥EG,得出∠EGF=∠AFB,设BF=2x,则AD=BC=6x,AF=AE=FG=3x,在Rt△ABF中,cos∠AFB==,即可得出结果.
【详解】
解:连接AF,如图所示:
∵四边形ABCD为矩形,
∴AD∥BC,AD=BC,
∴∠AEF=∠GFE,
由折叠的性质可知:∠AFE=∠GFE,AF=FG,
∴∠AEF=∠AFE,
∴AF=AE,
∴AE=FG,
∴四边形AFGE是菱形,
∴AF∥EG,
∴∠EGF=∠AFB,
设BF=2x,则AD=BC=6x,AF=AE=FG=3x,
在Rt△ABF中,cos∠AFB===,
∴cos∠EGF=,
故答案为:.
【点睛】
此题考查的是矩形与折叠问题、菱形的判定及性质、等腰三角形的性质和锐角三角函数,掌握矩形的性质、折叠的性质、菱形的判定及性质、等角对等边和等角的锐角三角函数值相等是解决此题的关键.
17.或
【解析】
【分析】
(1)分别在、、中应用含角的直角三角形的性质以及勾股定理求得,,再根据垂直平分线的性质、等边三角形的判定和性质、等腰三角形的判定求得,最后利用线段的和差即可求得答案;根据垂直平分线的性质、全等三角形的判定和性质、分线段成比例定理可证得,然后根据平行线的性质、相似三角形的判定和性质列出方程,解方程即可求得,最后利用线段的和差即可求得答案.
【详解】
解:①当时,如图1:
∵在中,,,
∴
∴
∵,
∴
∵
∴
∴ 在中,设,则
∵
∴
∴
∴,
∵垂直平分线段
∴
∵
∴是等边三角形
∴
∴
∴;
②当时,连接、交于点,过点作于,如图2:
设,则,
∵垂直平分线段,点是的中点
∴
∵
∴
∵
∵
∴垂直平分线段
∴
∵,
∴
∴
∵
∴,
∴
∴
∴
∴
∴
∴
∴.
∴综上所述,满足条件的的值为6或.
故答案是:6或
【点睛】
本题考查了垂直平分线的性质和判定、含角的直角三角形的性质、勾股定理、全等三角形的判定和性质、平行线的判定和性质、相似三角形的判定和性质、等边三角形的判定和性质等,渗透了逻辑推理的核心素养以及分类讨论的数学思想.
18.
【解析】
【分析】
由折叠的性质得出△A'EF为等腰直角三角形,得出EF=A'E=2,∠EFC'=45°,求出AF=AE+EF=+2,证明△ABF为等腰直角三角形,求出AB的长,证明△FDH∽△EAB,由相似三角形的性质得出,求出DF的长,则可得出答案.
【详解】
解:∵AE=A'E,
∴A'E=,
∵A'E=A'F,∠EA'B=∠EAB=90°,
∴△A'EF为等腰直角三角形,
∴EF=A'E=2,∠EFC'=45°,
∴AF=AE+EF=+2,△ABF为等腰直角三角形,
∴AB=AF=+2,∠ABF=45°,
∴∠ABE=∠HBF=22.5°,
∴∠AEB=67.5°,
∵将矩形ABCD再沿FH折叠,D与C'恰好重合,
∴∠C'FH=∠DFH=67.5°,
∴∠AEB =∠DFH,
又∵∠A=∠D,
∴△FDH∽△EAB,
∴,
∵DH=C'H=CH,
∴DH=
∴DF=AE=,
∴AD=AE+EF+DF=+2.
故答案为:+2.
【点睛】
本题考查了三角形相似的判定与性质,折叠的性质,矩形的性质,熟练掌握折叠的性质是解题的关键.
19.3
【解析】
【分析】
根据直角三角形的性质得到AB=10,利用勾股定理求出AC,再说明DE∥AC,得到,即可求出DE.
【详解】
解:∵∠ACB=90°,点D为AB中点,
∴AB=2CD=10,
∵BC=8,
∴AC==6,
∵DE⊥BC,AC⊥BC,
∴DE∥AC,
∴,即,
∴DE=3,
故答案为:3.
【点睛】
本题考查了直角三角形的性质,勾股定理,平行线分线段成比例,解题的关键是通过平行得到比例式.
20.避雷针BC的长度为4.8米.
【解析】
【分析】
解直角三角形求出CD,BD,根据BC=CD-BD求解即可.
【详解】
解:在Rt△ABD中,∵,
∴1.48=,
∵AD=80米,
∴BD=118.4(米),
在Rt△CAD中,∵tan∠CAD=,
∴1.54=,
∴CD=123.2(米),
∴BC=CD-BD=4.8(米)
答:避雷针BC的长度为4.8米.
【点睛】
本题考查解直角三角形的应用,解题的关键是熟练掌握基本知识,属于中考常考题型.
21.船的航行速度为m/min.
【解析】
【分析】
连接AB,过点C作CD⊥AB交于点D,根据题意得出,,CD=6米,利用锐角三角函数得出米,米,结合图形及速度求法即可得出结果.
【详解】
解:如图所示,连接AB,过点C作CD⊥AB交于点D,根据题意可得:
,,CD=6米,
在中,
(米),
在中,
米,
∴ 米,
∵船长为3米,
∴船航行距离为:米,
∴船的速度为:,
答:船的航行速度为m/min.
【点睛】
本题主要考查锐角三角函数的实际应用,理解题意,构建直角三角形是解题关键.
22.(1)答案见解析;(2).
【解析】
【分析】
(1)利用平行四边形的性质分别作出AB、AC的中点E、F,再利用三角形重心的性质即可作出△ABC的BC边上的中线AD;
(2)利用平行线的性质可得∠AEC=∠FDC,再利用菱形及等边三角形的性质可求得DH、CH的长,继而求得CD的长,从而求得答案.
【详解】
(1)如图,线段AD就是所求作的中线;
(2)如图:在的正三角形的网格中,
∵MN∥AB∥FD,
∴∠AEC=∠FDC,
∵四边形CMGN为菱形,且边长为5,
∴CG⊥MN,
∴CG⊥FD,
,
∴CG=2OG=5,
∵△GFD为等边三角形,且边长为2,
同理:HG=,
∴在Rt△CDH中,∠CHD=90,DH=1,CH=CG-HG=4,
∴,即,
∴,
∴.
【点睛】
本题考查了作图-应用与设计作图,菱形的性质、等边三角形的性质,平行线的性质,勾股定理的应用.首先要理解题意,弄清问题中对所作图形的要求,结合对应几何图形的性质和基本作图的方法作图.
23.42m
【解析】
【分析】
如图,过点A作,垂足为E.利用,求解即可.
【详解】
解:如图,过点A作,垂足为E.
由题意可知,,,.
在中,,
∴.
在中,,
.
∵,
∴
.
答:该建筑的高度约为.
【点睛】
本题考查了解斜三角形,通过作高化斜三角形为直角三角形,并准确求解是解题的关键.
24.(1)图3中CD′的长度比图2中CD的长度收缩了米;(2)该遮阳篷落在窗户AB上的阴影长度为米.
【解析】
【分析】
(1)解直角△ACD,求出CD,再解直角△BCD′,求出CD′,然后计算CD﹣CD′的长度即可;
(2)图3中遮阳蓬的长度为图2中CD的长度时,过D作DE∥BD′,交AB于E,解直角△ECD,求出CE,再计算CE-BC即可.
【详解】
(1)在直角△ACD中,∵AC=AB+BC=2米,∠CAD=30°,
∴tan∠CAD=,
∴CD=AC tan∠CAD=2×=(米).
在直角△BCD′中,∵BC=0.5米,∠CBD′=60°,
∴tan∠CBD′=,
∴CD′=BC tan∠CBD′=0.5×=(米),
∴CD﹣CD′=﹣=(米).
故图3中CD′的长度比图2中CD的长度收缩了米;
(2)如图,图3中遮阳篷的长度为图2中CD的长度时,过D作DE∥BD′,交AB于E.
在直角△ECD中,∵CD=米,∠CED=60°,
∴tan∠CED=,
∴CE===,
∴BE=CE﹣BC=﹣0.5=(米).
故该遮阳篷落在窗户AB上的阴影长度为米.
【点睛】
本题考查了解直角三角形的实际应用,掌握解直角三角形的方法是解题的关键.
25.(1)见解析;(2)28;(3)(2a,2b).
【解析】
【分析】
(1)连接OB,延长OB到B1使得OB1=2OB,同法作出A1,C1,连接A1C1,B1C1,A1B1即可.
(2)两条分割法求出三角形的面积即可.
(3)利用相似三角形的性质解决问题即可.
【详解】
解:(1)△A1B1C1即为所求.
(2)△A1B1C1的面积=4S△ABC=4×(4×5﹣×3×5﹣×1×3﹣×2×4)=28,
故答案为:28.
(3)点P(a,b)为△ABC内一点,则在△A1B1C1内的对应点P’的坐标为(2a,2b),
故答案为:(2a,2b).
【点睛】
本题考查作图——位似变换,三角形的面积等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
一、单选题
1.如图,在△ABC中,点G为△ABC的重心,过点G作DE∥BC,分别交AB、AC于点D、E,则△ADE与四边形DBCE的面积比为( )
A. B. C. D.
2.如果,那么的结果是( )
A. B. C. D.
3.在中,,则的值是( ).
A. B. C. D.
4.如图,菱形 ABCD 的边长为4 ,A 60, M 是 AD 的中点, N 是 AB 边上一动点, 将AMN 沿 MN 所在的直线翻折得到AMN ,连接 AC ,则当 AC 取得最小值时, tan DCA的值为( )
A. B. C. D.
5.如图,小明在一条东西走向公路的O处,测得图书馆A在他的北偏东方向,且与他相距,则图书馆A到公路的距离为( )
A. B. C. D.
6.在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角形△ADE(不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形△ADE只算一个),这样的格点三角形一共有( )
A.4个 B.5个 C.6个 D.7个
7.若为锐角,,则等于( )
A. B. C. D.
8.如图,AD//BC,∠D=90°,AD=3,BC=4,DC=6,若在边 DC上有点P,使△PAD 与△PBC相似,则这样的点 P 有( )
A.1 个 B.2 个 C.3 个 D.4 个
9.如图,将一张宽为2cm的长方形纸片沿AB折叠成如图所示的形状,那么折痕AB的长为( )cm
A. B. C.2 D.
10.在如图所示的网格中,以点为位似中心,四边形的位似图形是( )
A.四边形 B.四边形
C.四边形 D.四边形
11.如图,在RtABC中,∠C=90°,AC=3cm,BC=4cm,D从A出发沿AC方向以1cm/s向终点C匀速运动,过点D作DEAB交BC于点E,过点E作EF⊥BC交AB于点F,当四边形ADEF为菱形时,点D运动的时间为( )s
A. B. C. D.
12.已知A、B两地相距10km,在地图上相距10cm,则这张地图的比例尺是( ).
A.100000:1 B.1000:1 C.1:100000 D.1:1000
二、填空题
13.若,则________.
14.如图,在矩形中,,垂足为点.若,,则的长为______.
15.如图,在矩形中,,,点为边上的一个动点、过点作交边于点,把线段绕点旋转至(点与点对应),点落在线段上,若恰好平分,则的长为_________.
16.如图,矩形ABCD中,点E,F分别在AD,BC上,且AE=DE,BC=3BF,连接EF,将矩形ABCD沿EF折叠,点A恰好落在BC边上的点G处,则cos∠EGF的值为_____.
17.如图,在中,,,,是斜边上方一点,连接,点是的中点,垂直平分,交于点,连接,交于点,当为直角三角形时,线段的长为________.
18.如图,在矩形ABCD中,E,F为边AD上两点,将矩形ABCD沿BE折叠,点A恰好落在BF上的A'处,且A′E=A'F,再将矩形ABCD沿过点B的直线折叠,使点C落在BF上的C'处,折痕交CD于点H,将矩形ABCD再沿FH折叠,D与C'恰好重合.已知AE=,则AD=_____.
19.如图,在中,,点D是的中点,过点D作,垂足为点E,连接,若,,则________.
三、解答题
20.为了测量大楼顶上(居中)避雷针BC的长度,在地面上点A处测得避雷针底部B和顶部C的仰角分别为55°58′和57°,已知点A与楼底中间部位D的距离约为80米,求避雷针BC的长度.(参考数据:sin55°58′≈0.83,cos55°58′≈0.56,tan55°58′≈1.48,sin57°≈0.84,tan57°≈1.54)
21.五一期间,小明跟父母去乌镇旅游,欣赏乌镇水乡的美景.如图,当小明走到乌镇古桥的C处时,发现远处有一瞍船匀速行驶过来,当船行驶到A处时,小明测得船头的俯角为30°,同时小明开始计时,船在航行过小明所在的桥之后,继续向前航行到达B处,此时测得船尾的俯角为45°;从小明开始计时到船行驶至B处,共用时15min;已知小明所在位置距离水面6m,船长3m,船到水面的距离忽略不计,请你帮助小明计算一下船的航行速度(结果保留根号)
22.如图,在的正三角形的网格中,的三个顶点都在格点上.请按要求画图和计算:①仅用无刻度直尺;②保留作图痕迹.
(1)在图1中,画出的边上的中线.
(2)在图2中,求的值.
23.新冠肺炎疫情期间,我国各地采取了多种方式进行预防.其中,某地运用无人机规劝居民回家.如图,无人机于空中A处测得某建筑顶部B处的仰角为,测得该建筑底部C处的俯角为.若无人机的飞行高度为,求该建筑的高度(结果取整数),参考数据:,,.
24.如图1,某同学家的一面窗户上安装有遮阳篷,图2和图3是截面示意图,CD是遮阳篷,窗户AB为1.5米,BC为0.5米.该遮阳篷有伸缩功能.如图2,该同学在夏季某日的正午时刻测得太阳光和水平线的夹角为60°,遮阳篷CD正好将进入窗户AB的阳光挡住;如图3,该同学在冬季某日的正午时刻测得太阳光和水平线的夹角为30°,将遮阳篷收缩成CD′时,遮阳篷正好完全不挡进入窗户AB的阳光.
(1)计算图3中CD′的长度比图2中CD的长度收缩了多少米;(结果保留根号)
(2)如果图3中遮阳篷的长度为图2中CD的长度,请计算该遮阳篷落在窗户AB上的阴影长度为多少米?(请在图3中画图并标出相应字母,然后再计算)
25.如图,在边长为1的正方形网格中建立平面直角坐标系,已知△ABC三个顶点分别为A(﹣1,2)、B(2,1)、C(4,5).
(1)以原点O为位似中心,在x轴的上方画出△A1B1C1,使△A1B1C1与△ABC位似,且相似比为2;
(2)△A1B1C1的面积是 平方单位.
(3)点P(a,b)为△ABC内一点,则在△A1B1C1内的对应点P’的坐标为 .
参考答案:
1.A
【解析】
【分析】
连接AG并延长交BC于H,如图,利用三角形重心的性质得到AG=2GH,再证明△ADE∽△ABC,根据相似三角形的性质得到==,然后根据比例的性质得到△ADE与四边形DBCE的面积比.
【详解】
解:连接AG并延长交BC于H,如图,
∵点G为△ABC的重心,
∴AG=2GH,
∴=,
∵DE∥BC,
∴△ADE∽△ABC,
∴==()2=,
∴△ADE与四边形DBCE的面积比=.
故选:A.
【点睛】
本题考查了三角形的重心与相似三角形的性质与判定. 重心到顶点的距离与重心到对边中点的距离之比为2∶1.
2.B
【解析】
【分析】
根据比例的性质即可得到结论.
【详解】
∵=,
∴可设a=2k,b=3k,
∴==-.
故选B.
【点睛】
本题主要考查了比例的性质,解本题的要点根据题意可设a,b的值,从而求出答案.
3.C
【解析】
【分析】
首先根据勾股定理求得AC的长,然后根据正弦的定义即可求解.
【详解】
解:根据勾股定理可得:AC==,
∴sinB==.
故选:C.
【点睛】
本题主要考查了求一个角的正弦值,求出AC的长,正确理解正弦的定义是解题关键.
4.B
【解析】
【分析】
首先根据两点之间线段最短确定点的位置,再作MH⊥DC,然后根据菱形的性质可知MD,∠HDM,再根据30°直角三角形的性质求出HD和HM,进而求出CH,最后根据正切值定义求出答案即可.
【详解】
因为是定值,两点之间线段最短,即当点在MC上时,取最小值.
过点M作MH⊥DC于点H.
边长为4的菱形ABCD中,∠A=60°,
∵M为AD的中点,
∴2MD=AD=CD=4,∠HDM=60°,
∴∠MDH=∠HDM=60°,
∴∠HMD=30°,
∴,
∴,
∴CH=HD+CD=5,
∴,
∴的值为.
故选:B.
【点睛】
这是一道应用菱形的性质求线段最短问题,主要考查了菱形的性质,翻折的性质,锐角三角函数,直角三角形的性质等.
5.A
【解析】
【分析】
根据题意可得△OAB为直角三角形,∠AOB=30°,OA=200m,根据三角函数定义即可求得AB的长.
【详解】
解:由已知得,∠AOB=90°60°=30°,OA=200m.
则AB=OA=100m.
故选:A.
【点睛】
本题主要考查了解直角三角形的应用——方向角问题,正确记忆三角函数的定义是解决本题的关键.
6.C
【解析】
【分析】
根据题意,得出ABC的三边之比,并在直角坐标系中找出与ABC各边长成比例的相似三角形,并在直角坐标系中无一遗漏地表示出来.
【详解】
解:ABC的三边之比为,
如图所示,可能出现的相似三角形共有以下六种情况:
所以使得△ADE∽△ABC的格点三角形一共有6个,
故选:C.
【点睛】
本题考察了在直角坐标系中画出与已知三角形相似的图形,解题的关键在于找出与已知三角形各边长成比例的三角形,并在直角坐标系中无一遗漏地表示出来.
7.B
【解析】
【分析】
根据tan45°=1求出即可.
【详解】
∵∠A为锐角,tanA=1,∴∠A=45°.
故选B.
【点睛】
本题考查了特殊角的三角函数值,主要考查学生的记忆能力和计算能力.
8.A
【解析】
【分析】
根据已知分两种情况△PAD∽△PBC或△PAD∽△CBP来进行分析,求得PD的长,从而确定P存在的个数.
【详解】
解:∵AD∥BC,∠D=90°,
∴∠C=∠D=90°,
∵DC=6,AD=3,BC=4,
设PD=x,则PC=6-x.
①若PD:PC=AD:BC,则△PAD∽△PBC,
则,
解得:x=,
经检验:x=是原方程的解;
②若PD:BC=AD:PC,则△PAD∽△BPC,
则,
解得:x无解,
所以这样的点P存在的个数有1个.
故选:A.
【点睛】
此题考查了相似三角形的性质,熟练掌握相似三角形对应边成比例是解本题的关键.
9.A
【解析】
【分析】
作点A作,交BC于点D,作点B作,交AC于点E,根据长方形纸条的宽得出,继而可证明是等边三角形,则有,然后在直角三角形中利用锐角三角函数即可求出AB的值.
【详解】
作点A作,交BC于点D,作点B作,交AC于点E,
∵长方形的宽为2cm,
,
,
.
∴是等边三角形,
故选:A.
【点睛】
本题主要考查等边三角形的判定及性质,锐角三角函数,掌握等边三角形的判定及性质和特殊角的三角函数值是解题的关键.
10.A
【解析】
【分析】
以O为位似中心,作四边形ABCD的位似图形,根据图像可判断出答案.
【详解】
解:如图所示,四边形的位似图形是四边形.
故选:A
【点睛】
此题考查了位似图形的作法,画位似图形的一般步骤为:①确定位似中心;②分别连接并延长位似中心和能代表原图的关键点;③根据相似比,确定能代表所作的位似图形的关键点;顺次连接上述各点,确定位似图形.
11.D
【解析】
【分析】
由勾股定理可求AB的长,由锐角三角函数可得 ,即可求解.
【详解】
解:设经过t秒后,四边形ADEF是菱形,
∴AD=DE=t,DE∥AB,
∴CD=(3-t)(cm),∠ABC=∠DEC,
∵∠C=90°,AC=3cm,BC=4cm,
∴ (cm),
∵sin∠DEC=sin∠ABC=,
∴ ,
∴ ,
故选:D.
【点睛】
本题考查了菱形的性质,勾股定理,锐角三角函数等知识,灵活运用这些性质解决问题是本题的关键.
12.C
【解析】
【分析】
比例尺=图上距离:实际距离,根据题意可直接求得比例尺.
【详解】
∵10km=1000000cm,
∴比例尺为10:1000000=1:100000.
故选C.
【点睛】
掌握比例尺的计算方法,注意在求比的过程中,单位要统一.比例尺=图上距离:实际距离,图上距离在前,实际距离在后.
13.
【解析】
【分析】
设,,代入求解即可.
【详解】
由可设,,k是非零整数,
则.
故答案为:.
【点睛】
本题主要考查了比例的基本性质,准确利用性质变形是解题的关键.
14.3
【解析】
【分析】
在中,由正弦定义解得,再由勾股定理解得DE的长,根据同角的余角相等,得到,最后根据正弦定义解得CD的长即可解题.
【详解】
解:在中,
在矩形中,
故答案为:3.
【点睛】
本题考查矩形的性质、正弦、勾股定理等知识,是重要考点,难度较易,掌握相关知识是解题关键.
15.4
【解析】
【分析】
因为PQ∥AC,可得tan∠QPB=tan∠ACB=,设QB=4x,BP=3x,则QP=5x,PE=PB=3x,QE=5x 3x=2x,因为AE恰好平分∠BAC,可得∠CAE=∠QAE=∠QEA,所以AQ=QE=2x,AB=AQ+QB=2x+4x=6x=8,解得x的值,即可得出BP的长.
【详解】
解:如图,
∵在矩形ABCD中,AB=8,BC=6,
∴tan∠ACB==,
∵PQ∥AC,
∴∠QPB=∠ACB,
∴tan∠QPB=tan∠ACB=,
设QB=4x,BP=3x,
则QP=5x,
∵把线段PB绕点P旋转至PE(点B与点E对应),点E落在线段PQ上,
∴PE=PB=3x,QE=5x 3x=2x,
∵AE恰好平分∠BAC,
∴∠CAE=∠QAE,
∵PQ∥AC,
∴∠QEA=∠CAE,
∴∠QEA=∠QAE,
∴AQ=QE=2x,
∴AB=AQ+QB=2x+4x=6x=8,
∴BP=3x=4.
故答案为:4.
【点睛】
本题考查图形旋转的性质,锐角三角函数的定义,平行线的性质和角平分线的定义,等腰三角形的判定.解题的关键是掌握图形旋转的性质.
16.
【解析】
【分析】
连接AF,由矩形的性质得AD∥BC,AD=BC,由平行线的性质得∠AEF=∠GFE,由折叠的性质得∠AFE=∠GFE,AF=FG,推出∠AEF=∠AFE,则AF=AE,AE=FG,得出四边形AFGE是菱形,则AF∥EG,得出∠EGF=∠AFB,设BF=2x,则AD=BC=6x,AF=AE=FG=3x,在Rt△ABF中,cos∠AFB==,即可得出结果.
【详解】
解:连接AF,如图所示:
∵四边形ABCD为矩形,
∴AD∥BC,AD=BC,
∴∠AEF=∠GFE,
由折叠的性质可知:∠AFE=∠GFE,AF=FG,
∴∠AEF=∠AFE,
∴AF=AE,
∴AE=FG,
∴四边形AFGE是菱形,
∴AF∥EG,
∴∠EGF=∠AFB,
设BF=2x,则AD=BC=6x,AF=AE=FG=3x,
在Rt△ABF中,cos∠AFB===,
∴cos∠EGF=,
故答案为:.
【点睛】
此题考查的是矩形与折叠问题、菱形的判定及性质、等腰三角形的性质和锐角三角函数,掌握矩形的性质、折叠的性质、菱形的判定及性质、等角对等边和等角的锐角三角函数值相等是解决此题的关键.
17.或
【解析】
【分析】
(1)分别在、、中应用含角的直角三角形的性质以及勾股定理求得,,再根据垂直平分线的性质、等边三角形的判定和性质、等腰三角形的判定求得,最后利用线段的和差即可求得答案;根据垂直平分线的性质、全等三角形的判定和性质、分线段成比例定理可证得,然后根据平行线的性质、相似三角形的判定和性质列出方程,解方程即可求得,最后利用线段的和差即可求得答案.
【详解】
解:①当时,如图1:
∵在中,,,
∴
∴
∵,
∴
∵
∴
∴ 在中,设,则
∵
∴
∴
∴,
∵垂直平分线段
∴
∵
∴是等边三角形
∴
∴
∴;
②当时,连接、交于点,过点作于,如图2:
设,则,
∵垂直平分线段,点是的中点
∴
∵
∴
∵
∵
∴垂直平分线段
∴
∵,
∴
∴
∵
∴,
∴
∴
∴
∴
∴
∴
∴.
∴综上所述,满足条件的的值为6或.
故答案是:6或
【点睛】
本题考查了垂直平分线的性质和判定、含角的直角三角形的性质、勾股定理、全等三角形的判定和性质、平行线的判定和性质、相似三角形的判定和性质、等边三角形的判定和性质等,渗透了逻辑推理的核心素养以及分类讨论的数学思想.
18.
【解析】
【分析】
由折叠的性质得出△A'EF为等腰直角三角形,得出EF=A'E=2,∠EFC'=45°,求出AF=AE+EF=+2,证明△ABF为等腰直角三角形,求出AB的长,证明△FDH∽△EAB,由相似三角形的性质得出,求出DF的长,则可得出答案.
【详解】
解:∵AE=A'E,
∴A'E=,
∵A'E=A'F,∠EA'B=∠EAB=90°,
∴△A'EF为等腰直角三角形,
∴EF=A'E=2,∠EFC'=45°,
∴AF=AE+EF=+2,△ABF为等腰直角三角形,
∴AB=AF=+2,∠ABF=45°,
∴∠ABE=∠HBF=22.5°,
∴∠AEB=67.5°,
∵将矩形ABCD再沿FH折叠,D与C'恰好重合,
∴∠C'FH=∠DFH=67.5°,
∴∠AEB =∠DFH,
又∵∠A=∠D,
∴△FDH∽△EAB,
∴,
∵DH=C'H=CH,
∴DH=
∴DF=AE=,
∴AD=AE+EF+DF=+2.
故答案为:+2.
【点睛】
本题考查了三角形相似的判定与性质,折叠的性质,矩形的性质,熟练掌握折叠的性质是解题的关键.
19.3
【解析】
【分析】
根据直角三角形的性质得到AB=10,利用勾股定理求出AC,再说明DE∥AC,得到,即可求出DE.
【详解】
解:∵∠ACB=90°,点D为AB中点,
∴AB=2CD=10,
∵BC=8,
∴AC==6,
∵DE⊥BC,AC⊥BC,
∴DE∥AC,
∴,即,
∴DE=3,
故答案为:3.
【点睛】
本题考查了直角三角形的性质,勾股定理,平行线分线段成比例,解题的关键是通过平行得到比例式.
20.避雷针BC的长度为4.8米.
【解析】
【分析】
解直角三角形求出CD,BD,根据BC=CD-BD求解即可.
【详解】
解:在Rt△ABD中,∵,
∴1.48=,
∵AD=80米,
∴BD=118.4(米),
在Rt△CAD中,∵tan∠CAD=,
∴1.54=,
∴CD=123.2(米),
∴BC=CD-BD=4.8(米)
答:避雷针BC的长度为4.8米.
【点睛】
本题考查解直角三角形的应用,解题的关键是熟练掌握基本知识,属于中考常考题型.
21.船的航行速度为m/min.
【解析】
【分析】
连接AB,过点C作CD⊥AB交于点D,根据题意得出,,CD=6米,利用锐角三角函数得出米,米,结合图形及速度求法即可得出结果.
【详解】
解:如图所示,连接AB,过点C作CD⊥AB交于点D,根据题意可得:
,,CD=6米,
在中,
(米),
在中,
米,
∴ 米,
∵船长为3米,
∴船航行距离为:米,
∴船的速度为:,
答:船的航行速度为m/min.
【点睛】
本题主要考查锐角三角函数的实际应用,理解题意,构建直角三角形是解题关键.
22.(1)答案见解析;(2).
【解析】
【分析】
(1)利用平行四边形的性质分别作出AB、AC的中点E、F,再利用三角形重心的性质即可作出△ABC的BC边上的中线AD;
(2)利用平行线的性质可得∠AEC=∠FDC,再利用菱形及等边三角形的性质可求得DH、CH的长,继而求得CD的长,从而求得答案.
【详解】
(1)如图,线段AD就是所求作的中线;
(2)如图:在的正三角形的网格中,
∵MN∥AB∥FD,
∴∠AEC=∠FDC,
∵四边形CMGN为菱形,且边长为5,
∴CG⊥MN,
∴CG⊥FD,
,
∴CG=2OG=5,
∵△GFD为等边三角形,且边长为2,
同理:HG=,
∴在Rt△CDH中,∠CHD=90,DH=1,CH=CG-HG=4,
∴,即,
∴,
∴.
【点睛】
本题考查了作图-应用与设计作图,菱形的性质、等边三角形的性质,平行线的性质,勾股定理的应用.首先要理解题意,弄清问题中对所作图形的要求,结合对应几何图形的性质和基本作图的方法作图.
23.42m
【解析】
【分析】
如图,过点A作,垂足为E.利用,求解即可.
【详解】
解:如图,过点A作,垂足为E.
由题意可知,,,.
在中,,
∴.
在中,,
.
∵,
∴
.
答:该建筑的高度约为.
【点睛】
本题考查了解斜三角形,通过作高化斜三角形为直角三角形,并准确求解是解题的关键.
24.(1)图3中CD′的长度比图2中CD的长度收缩了米;(2)该遮阳篷落在窗户AB上的阴影长度为米.
【解析】
【分析】
(1)解直角△ACD,求出CD,再解直角△BCD′,求出CD′,然后计算CD﹣CD′的长度即可;
(2)图3中遮阳蓬的长度为图2中CD的长度时,过D作DE∥BD′,交AB于E,解直角△ECD,求出CE,再计算CE-BC即可.
【详解】
(1)在直角△ACD中,∵AC=AB+BC=2米,∠CAD=30°,
∴tan∠CAD=,
∴CD=AC tan∠CAD=2×=(米).
在直角△BCD′中,∵BC=0.5米,∠CBD′=60°,
∴tan∠CBD′=,
∴CD′=BC tan∠CBD′=0.5×=(米),
∴CD﹣CD′=﹣=(米).
故图3中CD′的长度比图2中CD的长度收缩了米;
(2)如图,图3中遮阳篷的长度为图2中CD的长度时,过D作DE∥BD′,交AB于E.
在直角△ECD中,∵CD=米,∠CED=60°,
∴tan∠CED=,
∴CE===,
∴BE=CE﹣BC=﹣0.5=(米).
故该遮阳篷落在窗户AB上的阴影长度为米.
【点睛】
本题考查了解直角三角形的实际应用,掌握解直角三角形的方法是解题的关键.
25.(1)见解析;(2)28;(3)(2a,2b).
【解析】
【分析】
(1)连接OB,延长OB到B1使得OB1=2OB,同法作出A1,C1,连接A1C1,B1C1,A1B1即可.
(2)两条分割法求出三角形的面积即可.
(3)利用相似三角形的性质解决问题即可.
【详解】
解:(1)△A1B1C1即为所求.
(2)△A1B1C1的面积=4S△ABC=4×(4×5﹣×3×5﹣×1×3﹣×2×4)=28,
故答案为:28.
(3)点P(a,b)为△ABC内一点,则在△A1B1C1内的对应点P’的坐标为(2a,2b),
故答案为:(2a,2b).
【点睛】
本题考查作图——位似变换,三角形的面积等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
同课章节目录
