等腰三角形
图片预览






文档简介
课件34张PPT。给我最大快乐的,不是已懂的知识,
而是不断的学习.----高斯12.3.1等腰三角形的判定我们在上一节学习了等腰三角形的性质。现在你能回答我一些问题吗?1、等腰三角形的性质是什么?(1)等腰三角形的两个底角相等。
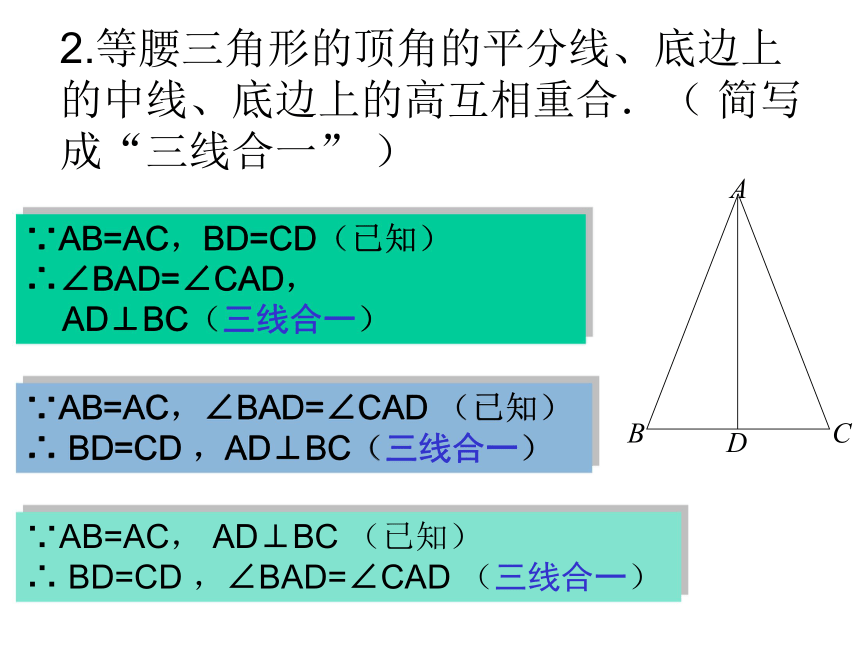
(可以简称:等边对等角)2 、等腰三角形的对称轴是什么?(2)等腰三角形的顶角平分线与底边上的中线,底边上的高互相重合(等腰三角形三线合一)问题2.等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合.( 简写成“三线合一” )∵AB=AC,BD=CD(已知)
∴∠BAD=∠CAD,
AD⊥BC(三线合一)∵AB=AC,∠BAD=∠CAD (已知)
∴ BD=CD ,AD⊥BC(三线合一)∵AB=AC, AD⊥BC (已知)
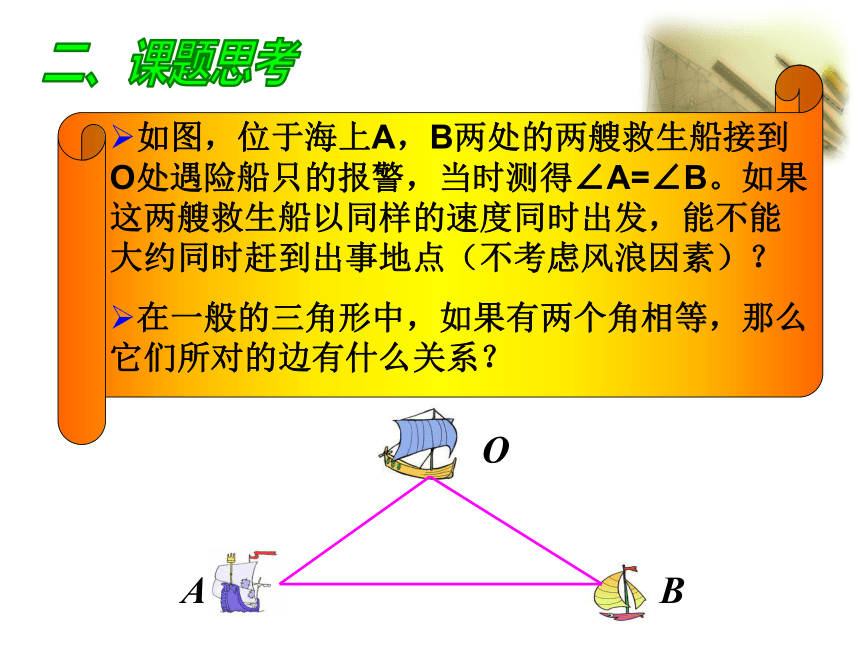
∴ BD=CD ,∠BAD=∠CAD (三线合一)思考1、等边对等角”的逆命题是什么? 如果一个三角形有两个角相等,那么这两个角所对的边也相等.2、这个命题成立吗?可以作为定理吗?二、课题思考ABO如果一个三角形有两个角相等,
那么这两个角所对的边也相等.简写成”等角对等边”.你能证明“等角对等边”吗?大胆猜测已知:∠B=∠C.
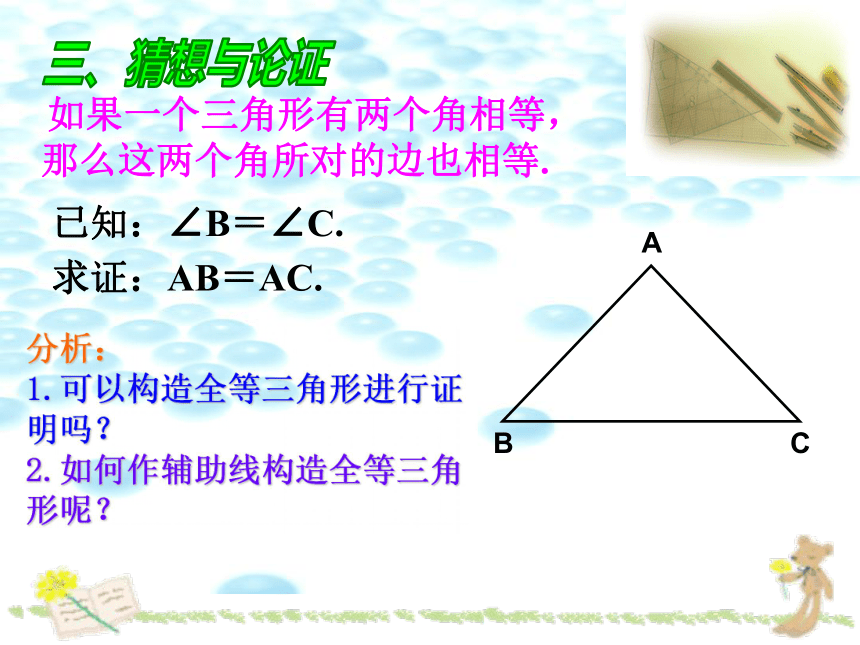
求证:AB=AC.三、猜想与论证 如果一个三角形有两个角相等,那么这两个角所对的边也相等.分析:
1.可以构造全等三角形进行证明吗?
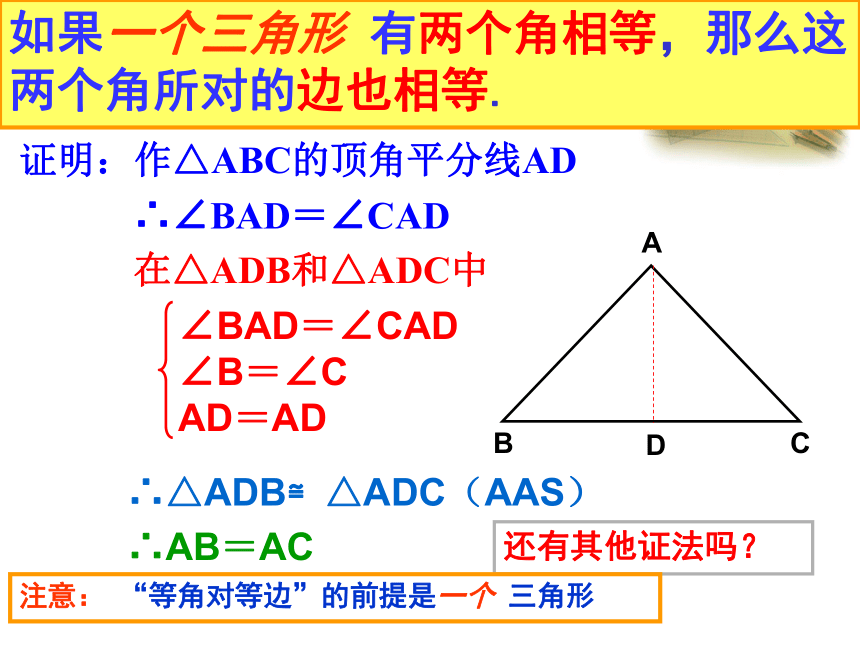
2.如何作辅助线构造全等三角形呢?证明:作△ABC的顶角平分线AD
∴∠BAD=∠CAD
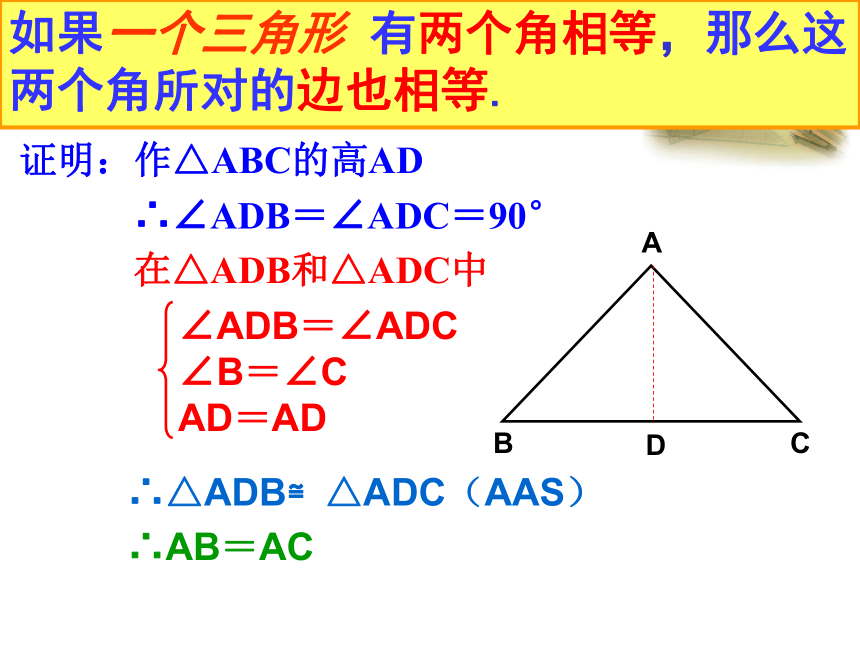
在△ADB和△ADC中方法一∴△ADB≌△ADC(AAS)∴AB=ACD如果一个三角形 有两个角相等,那么这两个角所对的边也相等.还有其他证法吗?注意: “等角对等边”的前提是一个 三角形证明:作△ABC的高AD
∴∠ADB=∠ADC=90°
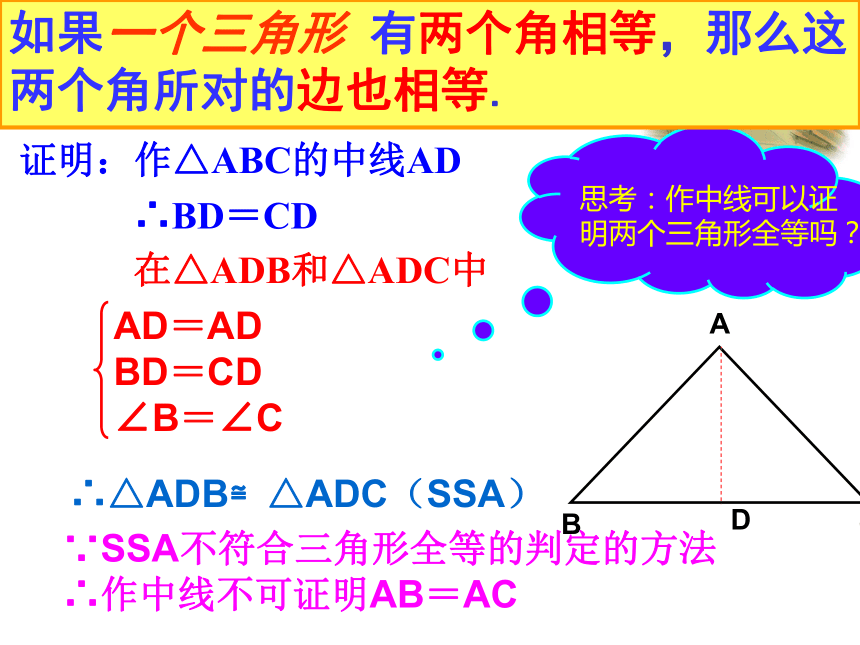
在△ADB和△ADC中方法二∴△ADB≌△ADC(AAS)∴AB=ACD如果一个三角形 有两个角相等,那么这两个角所对的边也相等.证明:作△ABC的中线AD
∴BD=CD
在△ADB和△ADC中方法三∴△ADB≌△ADC(SSA)思考:作中线可以证
明两个三角形全等吗?∵SSA不符合三角形全等的判定的方法
∴作中线不可证明AB=ACD如果一个三角形 有两个角相等,那么这两个角所对的边也相等.猜想与论证如果一个三角形有两个角相等,那么这两个角所对的边也相等已知:∠B=∠C求证:AB=AC几何语言:
∵∠B=∠C
∴AB=AC 结论简写:等角对等边等腰三角形的判定: 如果一个三角形中有两个角相等,那么这
两个角所对的边也相等.(简称为:等角对等边)等腰三角形的性质与判定有区别吗?性质是:等边 等角判定是:等角 等边练习1:已知AB∥CD,OA=OB.
求证:OC=OD.四、课堂思考证明:∵AB∥CD
∴∠A=∠C,∠B=∠D
又∵OA=OB
∴∠A=∠B
∴∠C=∠D
∴OC=OD练习2:已知AD∥BC,BD平分∠ABC
求证:AB=AD.四、课堂思考证明:∵AD∥BC
∴∠ADB=∠CBD
又∵BD平分∠ABC
∴∠ABD=∠CBD
∴∠ABD=∠ADB
∴AB=AD已知:如图,⊿ABC中, ∠ A=∠B=∠C
求证:AB=AC=BC
证明:在⊿ABC中
∵ ∠ A=∠B(已知)
∴BC=CA(等角对等边)
同理CA=AB
∴BC=CA=AB
例2:求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知:∠CAE是△ABC的外角,∠1=∠2,AD∥BC.
求证:AB=AC.五、例题思考【解析】要证明AB=AC,可先证明∠B=∠C. 因为∠1=∠2,所以可以设法找出∠B、∠C与∠1、∠2的关系. 例2:求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知:∠CAE是△ABC的外角,∠1=∠2,AD∥BC.
求证:AB=AC.五、例题思考证明:∵AD∥BC
∴∠1=∠B,∠2=∠C
又∵∠1=∠2
∴∠B=∠C
∴AB=AC问题:1.如右图所示△ABC是等腰三角形,AB=AC,倘若一不留心.它的一部分被墨水涂没了,只留下一条底边BC和一个底角∠C.同学们想一想,有没有办法把原来的等腰三角形ABC重新画出来?大家试试看.ABCBC方法一:用角的相等来画.BCA方法二:用过一边中点作垂线的方法来画.BCA请你解决问题考考大家:已知等腰三角形的底边等于a,底边上的高等于b,你能用尺规作图的方法作出这个等腰三角形吗?
ab 例3:如图,标杆AB高5m ,为了将它固定,需要由它的中点C向地面上与点B距离相等的D、E两点拉两条绳子,使得点D、B、E在一条直线上,量得DE=4m,绳子CD和CE要多长?五、例题思考【解析】显然绳长CD和CE是相等的. 问题实际上就是已知底边和底边上的高求等腰三角形的腰长,如果我们能以适当的比例画出这个等腰三角形,量出它的腰长,就能得到绳长了.五、例题思考 例3:如图,标杆AB高5m ,为了将它固定,需要由它的中点C向地面上与点B距离相等的D、E两点拉两条绳子,使得点D、B、E在一条直线上,量得DE=4m,绳子CD和CE要多长?解:选取比例尺为1:00(即以1cm代表1m)
(1)作线段DE=4cm;
(2)作DE的垂直平分线MN,与DE交于点B;
(3)在MN上截取BC=2.5cm
(4)连接CD、CE,△CDE就是所求的等腰三角形,量出CD的长,就可以计算出要求的绳长,自己试一试!MNBC综合运用1、如图△ABC中,AB=AC,∠B=36°,D、E分别是BC边上两点,且∠ADE=∠AED=2∠BAD,则图中等腰三角形有( )个。
C共有6个。
即△ABC、△ ADE、△ AEC、△ ABD、△ ABE。△ ADC、2、如图,把一张矩形的纸沿对角线折叠,重合
的部分是一个等腰三角形吗?为什么?123解:重合部分是等腰三角形。理由:由ABDC是矩形知
AC∥BD
∴∠ 3= ∠ 2由沿对角线折叠知
∠ 1 = ∠ 2∴ ∠ 1= ∠ 3
∴ BG=GC(等角对等边)等腰三角形的判定定理:六、课堂小结如果一个三角形有两个角相等,那么这两个角所对的边也相等.(可以简写成:等角对等边)几何语言∵∠B=∠C
∴AB=AC 如图,AD是△ABC的角平分线,DE⊥AB于D,DF⊥AC于F. 求证:AE=AF.七、课后思考证明:∵AD是△ABC的角平分线,
DE⊥AB,DF⊥AC
∴DE=DF,∠AED=∠AFD=90°
∴∠1=∠2(等边对等角)
∴∠AED-∠1=∠AFD-∠2
∴∠3=∠4
∴AE=AF(等角对等边)思考:在△ABC中,已知 ,BO平分∠ABC,CO平分∠ACB.(1)请问图中有多少个等腰三角形?说明理由.(2)线段EF和线段EB,FC之间有没有关系?若有是什么关系?AB=ACAB≠ACEF过点O作直线EF//BC交AB于E,交AC于F.2.已知在等腰△ABC中,∠A=36°,∠ B=72°,∠C=72°,请同学们想一想,如何添一条线,将等腰△ABC分成两个等腰三角形?成功后,如何再添一条线,多得到一个等腰三角形?还可以继续吗?只要作∠ B的角平分线即可!
只要再做∠ BDC的角平分线即可!
以下步骤重复下去即可!
趣味数学如图,在△ABC中,AB=AC, ∠A=36°,你能把△ABC分成三个等腰
三角形吗?(提供两中以上不同的作图方案)ABC动手画一画2.在正方形ABCD内找一点P,使△PAB、△PBC、△PCD、△PAD都是等腰三角形,这样的P点有几个?在正方形ABCD外呢?
●●●●●BACD●●●●答:在正方形内的P点有5个
在正方形外的P点有4个,如图小小探索家这些点的位置有什么特色呢?小结:
1、等腰三角形的判定定理是什么?2、等腰三角形的判定方法有下列几种:
①定义 ②判定定理 3、等腰三角形的判定定理与性质定理
的区别是条件和结论刚好相反。4、运用等腰三角形的判定定理时,
应注意在同一个三角形中寄语 如果你智慧的双眼善于观察,善于发现,那你一定会觉得数学就在我们的身边。
老师相信:你辛勤的汗水一定会浇灌出智慧的花朵!再见!
而是不断的学习.----高斯12.3.1等腰三角形的判定我们在上一节学习了等腰三角形的性质。现在你能回答我一些问题吗?1、等腰三角形的性质是什么?(1)等腰三角形的两个底角相等。
(可以简称:等边对等角)2 、等腰三角形的对称轴是什么?(2)等腰三角形的顶角平分线与底边上的中线,底边上的高互相重合(等腰三角形三线合一)问题2.等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合.( 简写成“三线合一” )∵AB=AC,BD=CD(已知)
∴∠BAD=∠CAD,
AD⊥BC(三线合一)∵AB=AC,∠BAD=∠CAD (已知)
∴ BD=CD ,AD⊥BC(三线合一)∵AB=AC, AD⊥BC (已知)
∴ BD=CD ,∠BAD=∠CAD (三线合一)思考1、等边对等角”的逆命题是什么? 如果一个三角形有两个角相等,那么这两个角所对的边也相等.2、这个命题成立吗?可以作为定理吗?二、课题思考ABO如果一个三角形有两个角相等,
那么这两个角所对的边也相等.简写成”等角对等边”.你能证明“等角对等边”吗?大胆猜测已知:∠B=∠C.
求证:AB=AC.三、猜想与论证 如果一个三角形有两个角相等,那么这两个角所对的边也相等.分析:
1.可以构造全等三角形进行证明吗?
2.如何作辅助线构造全等三角形呢?证明:作△ABC的顶角平分线AD
∴∠BAD=∠CAD
在△ADB和△ADC中方法一∴△ADB≌△ADC(AAS)∴AB=ACD如果一个三角形 有两个角相等,那么这两个角所对的边也相等.还有其他证法吗?注意: “等角对等边”的前提是一个 三角形证明:作△ABC的高AD
∴∠ADB=∠ADC=90°
在△ADB和△ADC中方法二∴△ADB≌△ADC(AAS)∴AB=ACD如果一个三角形 有两个角相等,那么这两个角所对的边也相等.证明:作△ABC的中线AD
∴BD=CD
在△ADB和△ADC中方法三∴△ADB≌△ADC(SSA)思考:作中线可以证
明两个三角形全等吗?∵SSA不符合三角形全等的判定的方法
∴作中线不可证明AB=ACD如果一个三角形 有两个角相等,那么这两个角所对的边也相等.猜想与论证如果一个三角形有两个角相等,那么这两个角所对的边也相等已知:∠B=∠C求证:AB=AC几何语言:
∵∠B=∠C
∴AB=AC 结论简写:等角对等边等腰三角形的判定: 如果一个三角形中有两个角相等,那么这
两个角所对的边也相等.(简称为:等角对等边)等腰三角形的性质与判定有区别吗?性质是:等边 等角判定是:等角 等边练习1:已知AB∥CD,OA=OB.
求证:OC=OD.四、课堂思考证明:∵AB∥CD
∴∠A=∠C,∠B=∠D
又∵OA=OB
∴∠A=∠B
∴∠C=∠D
∴OC=OD练习2:已知AD∥BC,BD平分∠ABC
求证:AB=AD.四、课堂思考证明:∵AD∥BC
∴∠ADB=∠CBD
又∵BD平分∠ABC
∴∠ABD=∠CBD
∴∠ABD=∠ADB
∴AB=AD已知:如图,⊿ABC中, ∠ A=∠B=∠C
求证:AB=AC=BC
证明:在⊿ABC中
∵ ∠ A=∠B(已知)
∴BC=CA(等角对等边)
同理CA=AB
∴BC=CA=AB
例2:求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知:∠CAE是△ABC的外角,∠1=∠2,AD∥BC.
求证:AB=AC.五、例题思考【解析】要证明AB=AC,可先证明∠B=∠C. 因为∠1=∠2,所以可以设法找出∠B、∠C与∠1、∠2的关系. 例2:求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知:∠CAE是△ABC的外角,∠1=∠2,AD∥BC.
求证:AB=AC.五、例题思考证明:∵AD∥BC
∴∠1=∠B,∠2=∠C
又∵∠1=∠2
∴∠B=∠C
∴AB=AC问题:1.如右图所示△ABC是等腰三角形,AB=AC,倘若一不留心.它的一部分被墨水涂没了,只留下一条底边BC和一个底角∠C.同学们想一想,有没有办法把原来的等腰三角形ABC重新画出来?大家试试看.ABCBC方法一:用角的相等来画.BCA方法二:用过一边中点作垂线的方法来画.BCA请你解决问题考考大家:已知等腰三角形的底边等于a,底边上的高等于b,你能用尺规作图的方法作出这个等腰三角形吗?
ab 例3:如图,标杆AB高5m ,为了将它固定,需要由它的中点C向地面上与点B距离相等的D、E两点拉两条绳子,使得点D、B、E在一条直线上,量得DE=4m,绳子CD和CE要多长?五、例题思考【解析】显然绳长CD和CE是相等的. 问题实际上就是已知底边和底边上的高求等腰三角形的腰长,如果我们能以适当的比例画出这个等腰三角形,量出它的腰长,就能得到绳长了.五、例题思考 例3:如图,标杆AB高5m ,为了将它固定,需要由它的中点C向地面上与点B距离相等的D、E两点拉两条绳子,使得点D、B、E在一条直线上,量得DE=4m,绳子CD和CE要多长?解:选取比例尺为1:00(即以1cm代表1m)
(1)作线段DE=4cm;
(2)作DE的垂直平分线MN,与DE交于点B;
(3)在MN上截取BC=2.5cm
(4)连接CD、CE,△CDE就是所求的等腰三角形,量出CD的长,就可以计算出要求的绳长,自己试一试!MNBC综合运用1、如图△ABC中,AB=AC,∠B=36°,D、E分别是BC边上两点,且∠ADE=∠AED=2∠BAD,则图中等腰三角形有( )个。
C共有6个。
即△ABC、△ ADE、△ AEC、△ ABD、△ ABE。△ ADC、2、如图,把一张矩形的纸沿对角线折叠,重合
的部分是一个等腰三角形吗?为什么?123解:重合部分是等腰三角形。理由:由ABDC是矩形知
AC∥BD
∴∠ 3= ∠ 2由沿对角线折叠知
∠ 1 = ∠ 2∴ ∠ 1= ∠ 3
∴ BG=GC(等角对等边)等腰三角形的判定定理:六、课堂小结如果一个三角形有两个角相等,那么这两个角所对的边也相等.(可以简写成:等角对等边)几何语言∵∠B=∠C
∴AB=AC 如图,AD是△ABC的角平分线,DE⊥AB于D,DF⊥AC于F. 求证:AE=AF.七、课后思考证明:∵AD是△ABC的角平分线,
DE⊥AB,DF⊥AC
∴DE=DF,∠AED=∠AFD=90°
∴∠1=∠2(等边对等角)
∴∠AED-∠1=∠AFD-∠2
∴∠3=∠4
∴AE=AF(等角对等边)思考:在△ABC中,已知 ,BO平分∠ABC,CO平分∠ACB.(1)请问图中有多少个等腰三角形?说明理由.(2)线段EF和线段EB,FC之间有没有关系?若有是什么关系?AB=ACAB≠ACEF过点O作直线EF//BC交AB于E,交AC于F.2.已知在等腰△ABC中,∠A=36°,∠ B=72°,∠C=72°,请同学们想一想,如何添一条线,将等腰△ABC分成两个等腰三角形?成功后,如何再添一条线,多得到一个等腰三角形?还可以继续吗?只要作∠ B的角平分线即可!
只要再做∠ BDC的角平分线即可!
以下步骤重复下去即可!
趣味数学如图,在△ABC中,AB=AC, ∠A=36°,你能把△ABC分成三个等腰
三角形吗?(提供两中以上不同的作图方案)ABC动手画一画2.在正方形ABCD内找一点P,使△PAB、△PBC、△PCD、△PAD都是等腰三角形,这样的P点有几个?在正方形ABCD外呢?
●●●●●BACD●●●●答:在正方形内的P点有5个
在正方形外的P点有4个,如图小小探索家这些点的位置有什么特色呢?小结:
1、等腰三角形的判定定理是什么?2、等腰三角形的判定方法有下列几种:
①定义 ②判定定理 3、等腰三角形的判定定理与性质定理
的区别是条件和结论刚好相反。4、运用等腰三角形的判定定理时,
应注意在同一个三角形中寄语 如果你智慧的双眼善于观察,善于发现,那你一定会觉得数学就在我们的身边。
老师相信:你辛勤的汗水一定会浇灌出智慧的花朵!再见!
