北师大版数学八年级上册 4.3一次函数的图象 第2课时 一次函数的图象(二)课件(共20张PPT)
文档属性
| 名称 | 北师大版数学八年级上册 4.3一次函数的图象 第2课时 一次函数的图象(二)课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 350.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
第四章 一次函数
3 一次函数的图象
第2课时 一次函数的图象(二)
目录
01
本课目标
02
课堂演练
本课目标
1.会画一次函数的图象.
2.识记一次函数的图象与性质,并能灵活运用一次函数的图象与性质解答有关问题.
知识点一:一次函数的图象
一次函数y=kx+b的图象是一条_________,它经过点(0,_________).
知识重点
直线
b
对点范例
1.下列图象中,是一次函数y=-x+1的图象的为( )
A
知识点二:一次函数的性质
在一次函数y=kx+b中:
当k_________时,y的值随着x值的增大而增大;
当k_________时,y的值随着x值的增大而减小.
知识重点
>0
<0
对点范例
2.一次函数y=-2x+5的图象性质错误的是( )
A.y随x的增大而减小
B.直线经过第一、二、四象限
C.直线从左到右是下降的
D.直线与x轴的交点坐标是(0,5)
D
课堂演练
典例精析
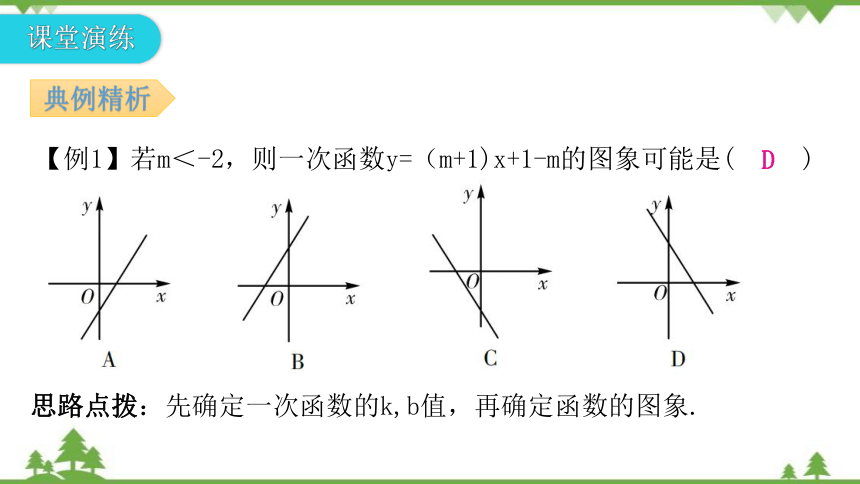
思路点拨:先确定一次函数的k,b值,再确定函数的图象.
【例1】若m<-2,则一次函数y=(m+1)x+1-m的图象可能是( )
D
举一反三
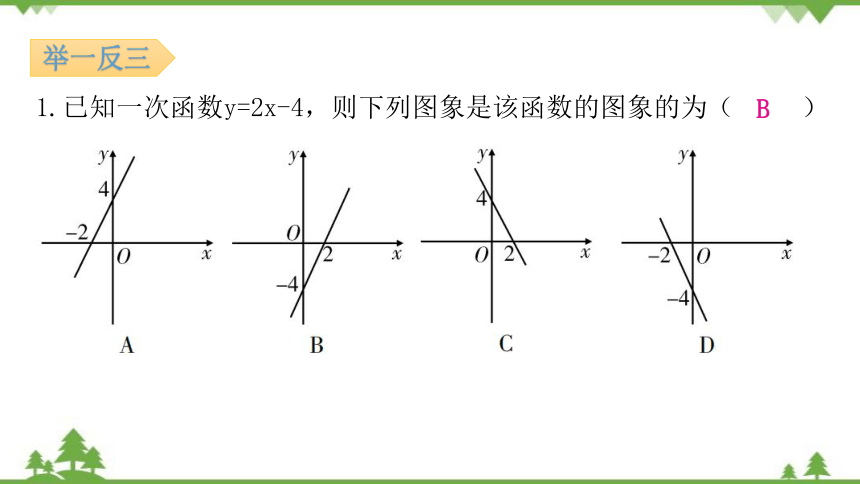
B
1.已知一次函数y=2x-4,则下列图象是该函数的图象的为( )
典例精析
【例2】已知一次函数y=x,y=x+3,y=-x,y=-x-3.
(1)在如图4-3-3所示直角坐标系中
画出这些函数的图象;(不用写画法)
解:(1)如答图4-3-2.
(2)根据(1)中所画图象回答下列问题:
①函数y=x+3的图象经过第____________象限,y随x的增大而_________,函数的图象从左到右逐渐_________;
②函数y=-x-3的图象经过第_____________象限,y随x的增大而_________,函数的图象从左到右逐渐_________;
③直线y=x+3_________直线y=x,直线y=x向_________平移_________个单位长度得到直线y=x+3;
直线y=-x-3平行于直线________,直线y=-x向_________平移_________个单位长度得到直线y=-x-3.
一、二、三
增大
上升
二、三、四
减小
下降
平行于
上
3
y=-x
下
3
思路点拨:与正比例函数一样,当k>0时,一次函数的y值随x值
的增大而增大;当k<0时,y值随x值的增大而减小,只是图象不
过原点.
举一反三
2. 已知一次函数y=-2x+2,y=x+2,y= x+2.
(1)在如图4-3-4所示直角坐标系中画出这些函数的图象;(不用写画法)
(2)根据(1)中所画图象回答下列问题:
直线y=-2x+2与x轴交于点_________,与y轴交于点_________,
直线y=x+2与x轴交于点_________,与y轴交于点_________,
直线y=12x+2与x轴交于点_________,与y轴交于点_________;
(1,0)
(0,2)
(-2,0)
(0,2)
(-4,0)
(0,2)
(3)结论归纳:
两条直线,当k相同,b不同时,它们互相_________,且都是由y=kx通过_________平移得到的;
两条直线,当k不同,b相同时,它们都与y轴交于点_________.
平行
上下
(0,b)
解:(1)如答图4-3-3.
典例精析
【例3】一次函数y=-3x+1的图象过点(x1,y1),(x1+1,y2),(x1+2,y3),则( )
A. y1<y2<y3 B. y3<y2<y1
C. y2<y1<y3 D.y3<y1<y2
思路点拨:先根据一次函数的解析式判断出函数的增减性,再根据x1B
3. 已知一次函数y=kx+3的图象经过点A,且y随x的增大而减小,则点A的坐标可以是( )
A. (-1,2) B. (1,-2)
C. (2,3) D.(3,4)
举一反三
B
谢 谢
第四章 一次函数
3 一次函数的图象
第2课时 一次函数的图象(二)
目录
01
本课目标
02
课堂演练
本课目标
1.会画一次函数的图象.
2.识记一次函数的图象与性质,并能灵活运用一次函数的图象与性质解答有关问题.
知识点一:一次函数的图象
一次函数y=kx+b的图象是一条_________,它经过点(0,_________).
知识重点
直线
b
对点范例
1.下列图象中,是一次函数y=-x+1的图象的为( )
A
知识点二:一次函数的性质
在一次函数y=kx+b中:
当k_________时,y的值随着x值的增大而增大;
当k_________时,y的值随着x值的增大而减小.
知识重点
>0
<0
对点范例
2.一次函数y=-2x+5的图象性质错误的是( )
A.y随x的增大而减小
B.直线经过第一、二、四象限
C.直线从左到右是下降的
D.直线与x轴的交点坐标是(0,5)
D
课堂演练
典例精析
思路点拨:先确定一次函数的k,b值,再确定函数的图象.
【例1】若m<-2,则一次函数y=(m+1)x+1-m的图象可能是( )
D
举一反三
B
1.已知一次函数y=2x-4,则下列图象是该函数的图象的为( )
典例精析
【例2】已知一次函数y=x,y=x+3,y=-x,y=-x-3.
(1)在如图4-3-3所示直角坐标系中
画出这些函数的图象;(不用写画法)
解:(1)如答图4-3-2.
(2)根据(1)中所画图象回答下列问题:
①函数y=x+3的图象经过第____________象限,y随x的增大而_________,函数的图象从左到右逐渐_________;
②函数y=-x-3的图象经过第_____________象限,y随x的增大而_________,函数的图象从左到右逐渐_________;
③直线y=x+3_________直线y=x,直线y=x向_________平移_________个单位长度得到直线y=x+3;
直线y=-x-3平行于直线________,直线y=-x向_________平移_________个单位长度得到直线y=-x-3.
一、二、三
增大
上升
二、三、四
减小
下降
平行于
上
3
y=-x
下
3
思路点拨:与正比例函数一样,当k>0时,一次函数的y值随x值
的增大而增大;当k<0时,y值随x值的增大而减小,只是图象不
过原点.
举一反三
2. 已知一次函数y=-2x+2,y=x+2,y= x+2.
(1)在如图4-3-4所示直角坐标系中画出这些函数的图象;(不用写画法)
(2)根据(1)中所画图象回答下列问题:
直线y=-2x+2与x轴交于点_________,与y轴交于点_________,
直线y=x+2与x轴交于点_________,与y轴交于点_________,
直线y=12x+2与x轴交于点_________,与y轴交于点_________;
(1,0)
(0,2)
(-2,0)
(0,2)
(-4,0)
(0,2)
(3)结论归纳:
两条直线,当k相同,b不同时,它们互相_________,且都是由y=kx通过_________平移得到的;
两条直线,当k不同,b相同时,它们都与y轴交于点_________.
平行
上下
(0,b)
解:(1)如答图4-3-3.
典例精析
【例3】一次函数y=-3x+1的图象过点(x1,y1),(x1+1,y2),(x1+2,y3),则( )
A. y1<y2<y3 B. y3<y2<y1
C. y2<y1<y3 D.y3<y1<y2
思路点拨:先根据一次函数的解析式判断出函数的增减性,再根据x1
3. 已知一次函数y=kx+3的图象经过点A,且y随x的增大而减小,则点A的坐标可以是( )
A. (-1,2) B. (1,-2)
C. (2,3) D.(3,4)
举一反三
B
谢 谢
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
