一次函数复习[上学期]

课件7张PPT。[复习要求]
(1)能在具体情境中体会一次函数的意义；
(2)能根据所给信息确定一次函数表达式；
(3)会画一次函数的图象，能根据一次函数的图象和表达式理解其性质；
(4)能利用一次函数及其图象解决简单的实际问题；
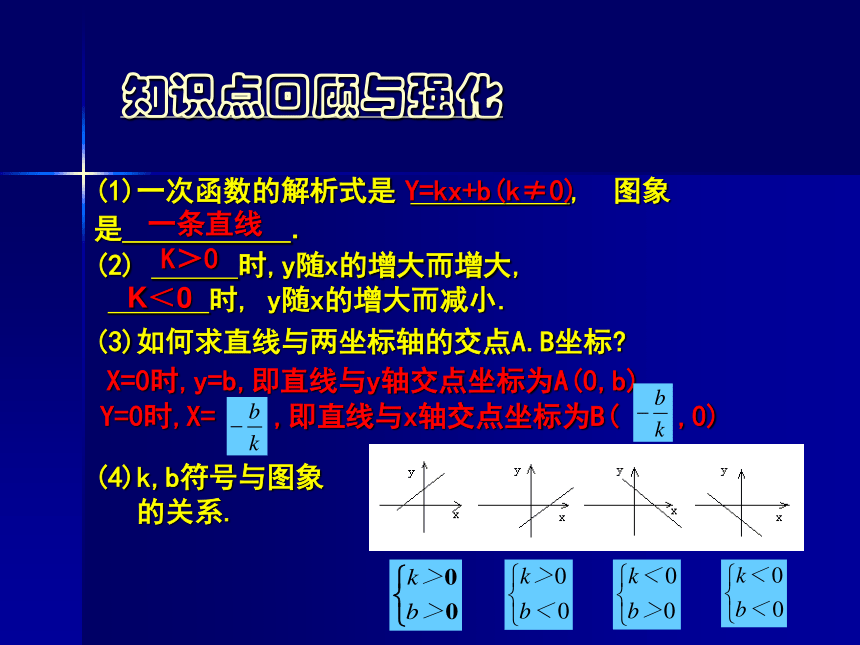
(5)初步体会方程和函数的关系．“一次函数”复习课知识点回顾与强化(1)一次函数的解析式是 , 图象是 . 　　　　　 (2) 时,y随x的增大而增大,
时, y随x的增大而减小.(3)如何求直线与两坐标轴的交点A.B坐标?(4)k,b符号与图象
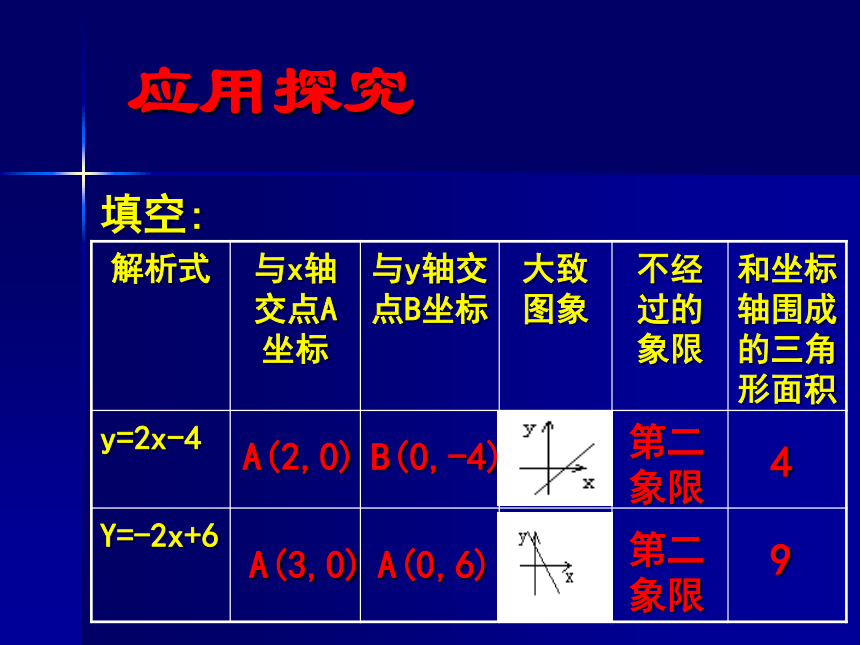
的关系.Y=kx+b(k≠0)一条直线K＞0K＜0X=0时,y=b,即直线与y轴交点坐标为A(0,b)Y=0时,X= ,即直线与x轴交点坐标为B( ,0)应用探究填空:A(2,0)B(0,-4)第二
象限4第二
象限9A(3,0)A(0,6)已知一次函数y=kx+b，根据图示条件，确定k，b值解：由图知，直线y=kx+b过点A（2，0），B（0，3）又由图知，两直线交于点A（2，0）。应用探究知识拓展一元次方程与一次函数的关系探讨X取何值时y＞0,y=0,y＜0?结论:一元一次方程的解实质是一次函数图象与坐标轴交点的坐标,这就是数与形的结合.我们不仅可以用代数方法算出一元次方程的解，还可以从一次函数的图象中看出来.
1.举例说明二元一次方程与一次函数的关系二元一次方程3x-y-6=0 一次函数y=3x-62.填表A(1,3)B(2,0)C(0,-6)D(-1,-9)结论:二元一次方程的每一组解就是
对应一次函数图象的坐标.知识拓展二元一次方程组与一次函数的关系探讨在同一坐标系中作y=-3x+1和y=2x-4的图象,并指出交点坐标.得出的结论是什么?二元一次方程组的解就是对应两个
一次函数图象的交点坐标.若求两直线交点坐标,该如何求?解方程组。知识拓展