人教版八年级数学上册11.3 多边形及其内角和阶段练习(含解析)
文档属性
| 名称 | 人教版八年级数学上册11.3 多边形及其内角和阶段练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 319.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 21:33:07 | ||
图片预览



文档简介
八年级数学11.3 多边形及其内角和阶段练习
一.选择题(共6小题)
1.下列度数中,不能成为多边形的内角和的是( )
A.540° B.280° C.1800° D.900°
2.从多边形一条边上的一点(不是顶点)处出发,连接各个顶点得到2021个三角形,则这个多边形的边数为( )
A.2023 B.2022 C.2021 D.2020
3.如图,将一张四边形纸片沿直线剪开,如果剪开后的两个图形的内角和相等,下列四种剪法中,符合要求的是( )
A.①② B.①③ C.②④ D.③④
4.设四边形的内角和等于a,六边形的外角和等于b,则a与b的关系是( )
A.a>b B.a<b C.a=b D.b=a+360°
5.衢州钟灵塔的塔基是个正n边形(n是正整数).测得塔基所在的正n边形的一个外角为60°,如图所示,n的值是( )
A.5 B.6 C.7 D.8
6.将正六边形与正五边形按如图所示方式摆放,公共顶点为O,且正六边形的边AB与正五边形的边DE在同一条直线上,则∠BOE的度数是( )
A.48° B.54° C.60° D.72°
二.填空题(共5小题)
7.若凸n边形的内角和为1260°,则n= ;该多边形的对角线条数是 .
8.如图是第四套人民币1角硬币,该硬币边缘镌刻的正多边形的外角的度数为 °.
9.若一个多边形的一条对角线把它分成两个四边形,则这个多边形的内角和是 度.
10.如图,直角三角形的两条直角边AC,BC分别经过正九边形的两个顶点,则图中∠1+∠2的结果是 .
11.如图,l1∥l2,五边形ABCDE是正五边形,那么∠1﹣∠2等于 度.
三.解答题(共5小题)
12.已知一个多边形的内角和与外角和的差为1080°,
(1)求这个多边形的边数;
(2)求此多边形的对角线条数.
13.如图,在五边形ABCDE中满足AB∥CD.
(1)求图形中的x的值;
(2)∠D、∠E的外角和比∠B、∠C的外角和小多少?
14.如图,淇淇从点A出发,前进10米后向右转20°,再前进10米后又向右转20°,这样一直下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.
(1)淇淇一共走了多少米?说明理由.
(2)求这个多边形的内角和.
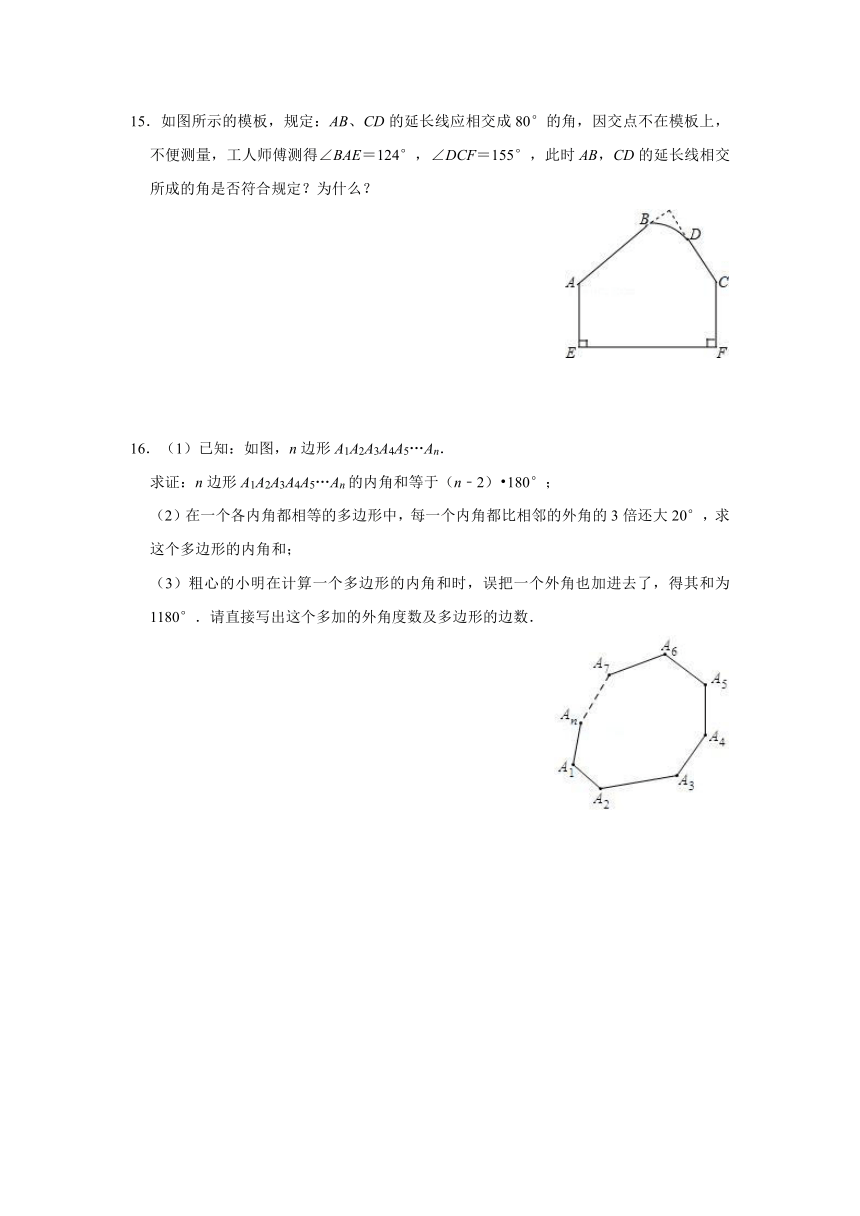
15.如图所示的模板,规定:AB、CD的延长线应相交成80°的角,因交点不在模板上,不便测量,工人师傅测得∠BAE=124°,∠DCF=155°,此时AB,CD的延长线相交所成的角是否符合规定?为什么?
16.(1)已知:如图,n边形A1A2A3A4A5…An.
求证:n边形A1A2A3A4A5…An的内角和等于(n﹣2) 180°;
(2)在一个各内角都相等的多边形中,每一个内角都比相邻的外角的3倍还大20°,求这个多边形的内角和;
(3)粗心的小明在计算一个多边形的内角和时,误把一个外角也加进去了,得其和为1180°.请直接写出这个多加的外角度数及多边形的边数.
参考答案
一.选择题(共6小题)
1.解:不是180的整数倍的选项只有第二个280度.
故选:B.
2.解:从多边形一条边上的一点(不是顶点)处出发,连接各个顶点得到2021个三角形,则这个多边形的边数为2021+1=2022.
故选:B.
3.解:∵①剪开后的两个图形是四边形,它们的内角和都是360°,③剪开后的两个图形是三角形,它们的内角和都是180°;
∴①③剪开后的两个图形的内角和相等,
故选:B.
4.解:∵四边形的内角和等于a,
∴a=(4﹣2)×180°=360°.
∵五边形的外角和等于b,
∴b=360°,
∴a=b.
故选:C.
5.解:∵正n边形的一个外角是60°,n边形的外角和为360°,
∴n=360÷60=6.
故选:B.
6.解:由题意得:∠DEO=108°,∠ABO=120°,
∴∠OEB=72°,∠OBE=60°,
∴∠BOE=180°﹣72°﹣60°=48°,
故选:A.
二.填空题(共5小题)
7.解:∵凸n边形的内角和为1260°,
∴(n﹣2)×180°=1260°,
解得n=9,
∴这个多边形的对角线的条数是9×(9﹣3)=27.
故答案为:9,27.
8.解:∵正多边形的外角和是360°,
∴360°÷9=40°.
故答案为:40.
9.解:由题意得,
两个四边形有一条公共边,得多边形是3+3=6,
由多边形内角和定理,
得(6﹣2)×180°=720°.
故答案为:720.
10.解:如图,
(9﹣2)×180°÷9×2
=7×180°÷9×2
=280°,
∠3+∠4=180°﹣90°=90°,
∠1+∠2=280°﹣90°=190°.
故答案为:190°.
11.解:如图,延长AB并交l2于点M.
∵五边形ABCDE是正五边形,
∴正五边形ABCDE的每个外角相等.
∴∠MBC72°.
∵l1∥l2,
∴∠2=∠BMD.
∵∠1=∠BMD+∠MBC,
∴∠BMD=∠1﹣∠MBC.
∴∠1﹣∠2=∠MBC=72°.
故答案为:72.
三.解答题(共5小题)
12.解:(1)设这个多边形的边数为n,
由题意得,(n﹣2)×180°﹣360°=1080°,
解得,n=10,
答:这个多边形的边数为10;
(2)此多边形的对角线条数10×(10﹣3)=35.
13.解:(1)∵AB∥CD,
∴∠B+∠C=180°,
∵在五边形ABCDE内角和为540°,
∴x=540﹣(∠A+∠D)﹣(∠B+∠C),
x=540﹣(125+150)﹣180,
x=540﹣275﹣180,
x=85;
(2)∠D、∠E的外角和=180°﹣150°+(180°﹣85°)=125°,
∠B、∠C的外角和=180°﹣∠B+180°﹣∠C=360°﹣(∠B+∠C)=180°,
180°﹣125°=55°.
14.解:(1)∵所经过的路线正好构成一个外角是20度的正多边形,
∴360÷20=18,18×10=180(米).
答:淇淇一共走了180米.
(2)根据题意,得(18﹣2)×180°=2880°,
答:这个多边形的内角和是2880°.
15.解:AB与CD的延长线交于点G,如图,
∵AE⊥EF,CF⊥EF,
∴∠E=∠F=90°,
∵∠BAE=124°,∠DCF=155°,
∴∠G=540°﹣(124°+155°+90°×2)
=540°﹣459°
=81°,
∵81°≠80°,
∴不符合规定.
16.解:(1)∵从n边形的一个顶点可以作(n﹣3)条对角线,
∴得出把三角形分割成的三角形个数为:n﹣3+1=n﹣2,
∵这(n﹣2)个三角形的内角和都等于180°,
∴n边形的内角和是(n﹣2)×180°;
(2)设多边形的一个外角为α°,则与其相邻的内角为(3α+20)°,
由题意,得(3α+20)+α=180,
解得α=40,
即多边形的每个外角为40°,
∵多边形的外角和为360°,
∴多边形的边数为360°÷40°=9,
内角和为(9﹣2)×180°=1260°,
答:这个多边形的内角和为1260°;
(3)设多边形的边数为n,多加的外角度数为α,则
(n﹣2) 180°=1180°﹣α,
∵1180°=6×180°+100°,内角和应是180°的倍数,
∴小明多加的一个外角为100°,
∴这是6+2=8边形的内角和.
答:这个外角的度数是100°,该多边形的边数是8.
一.选择题(共6小题)
1.下列度数中,不能成为多边形的内角和的是( )
A.540° B.280° C.1800° D.900°
2.从多边形一条边上的一点(不是顶点)处出发,连接各个顶点得到2021个三角形,则这个多边形的边数为( )
A.2023 B.2022 C.2021 D.2020
3.如图,将一张四边形纸片沿直线剪开,如果剪开后的两个图形的内角和相等,下列四种剪法中,符合要求的是( )
A.①② B.①③ C.②④ D.③④
4.设四边形的内角和等于a,六边形的外角和等于b,则a与b的关系是( )
A.a>b B.a<b C.a=b D.b=a+360°
5.衢州钟灵塔的塔基是个正n边形(n是正整数).测得塔基所在的正n边形的一个外角为60°,如图所示,n的值是( )
A.5 B.6 C.7 D.8
6.将正六边形与正五边形按如图所示方式摆放,公共顶点为O,且正六边形的边AB与正五边形的边DE在同一条直线上,则∠BOE的度数是( )
A.48° B.54° C.60° D.72°
二.填空题(共5小题)
7.若凸n边形的内角和为1260°,则n= ;该多边形的对角线条数是 .
8.如图是第四套人民币1角硬币,该硬币边缘镌刻的正多边形的外角的度数为 °.
9.若一个多边形的一条对角线把它分成两个四边形,则这个多边形的内角和是 度.
10.如图,直角三角形的两条直角边AC,BC分别经过正九边形的两个顶点,则图中∠1+∠2的结果是 .
11.如图,l1∥l2,五边形ABCDE是正五边形,那么∠1﹣∠2等于 度.
三.解答题(共5小题)
12.已知一个多边形的内角和与外角和的差为1080°,
(1)求这个多边形的边数;
(2)求此多边形的对角线条数.
13.如图,在五边形ABCDE中满足AB∥CD.
(1)求图形中的x的值;
(2)∠D、∠E的外角和比∠B、∠C的外角和小多少?
14.如图,淇淇从点A出发,前进10米后向右转20°,再前进10米后又向右转20°,这样一直下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.
(1)淇淇一共走了多少米?说明理由.
(2)求这个多边形的内角和.
15.如图所示的模板,规定:AB、CD的延长线应相交成80°的角,因交点不在模板上,不便测量,工人师傅测得∠BAE=124°,∠DCF=155°,此时AB,CD的延长线相交所成的角是否符合规定?为什么?
16.(1)已知:如图,n边形A1A2A3A4A5…An.
求证:n边形A1A2A3A4A5…An的内角和等于(n﹣2) 180°;
(2)在一个各内角都相等的多边形中,每一个内角都比相邻的外角的3倍还大20°,求这个多边形的内角和;
(3)粗心的小明在计算一个多边形的内角和时,误把一个外角也加进去了,得其和为1180°.请直接写出这个多加的外角度数及多边形的边数.
参考答案
一.选择题(共6小题)
1.解:不是180的整数倍的选项只有第二个280度.
故选:B.
2.解:从多边形一条边上的一点(不是顶点)处出发,连接各个顶点得到2021个三角形,则这个多边形的边数为2021+1=2022.
故选:B.
3.解:∵①剪开后的两个图形是四边形,它们的内角和都是360°,③剪开后的两个图形是三角形,它们的内角和都是180°;
∴①③剪开后的两个图形的内角和相等,
故选:B.
4.解:∵四边形的内角和等于a,
∴a=(4﹣2)×180°=360°.
∵五边形的外角和等于b,
∴b=360°,
∴a=b.
故选:C.
5.解:∵正n边形的一个外角是60°,n边形的外角和为360°,
∴n=360÷60=6.
故选:B.
6.解:由题意得:∠DEO=108°,∠ABO=120°,
∴∠OEB=72°,∠OBE=60°,
∴∠BOE=180°﹣72°﹣60°=48°,
故选:A.
二.填空题(共5小题)
7.解:∵凸n边形的内角和为1260°,
∴(n﹣2)×180°=1260°,
解得n=9,
∴这个多边形的对角线的条数是9×(9﹣3)=27.
故答案为:9,27.
8.解:∵正多边形的外角和是360°,
∴360°÷9=40°.
故答案为:40.
9.解:由题意得,
两个四边形有一条公共边,得多边形是3+3=6,
由多边形内角和定理,
得(6﹣2)×180°=720°.
故答案为:720.
10.解:如图,
(9﹣2)×180°÷9×2
=7×180°÷9×2
=280°,
∠3+∠4=180°﹣90°=90°,
∠1+∠2=280°﹣90°=190°.
故答案为:190°.
11.解:如图,延长AB并交l2于点M.
∵五边形ABCDE是正五边形,
∴正五边形ABCDE的每个外角相等.
∴∠MBC72°.
∵l1∥l2,
∴∠2=∠BMD.
∵∠1=∠BMD+∠MBC,
∴∠BMD=∠1﹣∠MBC.
∴∠1﹣∠2=∠MBC=72°.
故答案为:72.
三.解答题(共5小题)
12.解:(1)设这个多边形的边数为n,
由题意得,(n﹣2)×180°﹣360°=1080°,
解得,n=10,
答:这个多边形的边数为10;
(2)此多边形的对角线条数10×(10﹣3)=35.
13.解:(1)∵AB∥CD,
∴∠B+∠C=180°,
∵在五边形ABCDE内角和为540°,
∴x=540﹣(∠A+∠D)﹣(∠B+∠C),
x=540﹣(125+150)﹣180,
x=540﹣275﹣180,
x=85;
(2)∠D、∠E的外角和=180°﹣150°+(180°﹣85°)=125°,
∠B、∠C的外角和=180°﹣∠B+180°﹣∠C=360°﹣(∠B+∠C)=180°,
180°﹣125°=55°.
14.解:(1)∵所经过的路线正好构成一个外角是20度的正多边形,
∴360÷20=18,18×10=180(米).
答:淇淇一共走了180米.
(2)根据题意,得(18﹣2)×180°=2880°,
答:这个多边形的内角和是2880°.
15.解:AB与CD的延长线交于点G,如图,
∵AE⊥EF,CF⊥EF,
∴∠E=∠F=90°,
∵∠BAE=124°,∠DCF=155°,
∴∠G=540°﹣(124°+155°+90°×2)
=540°﹣459°
=81°,
∵81°≠80°,
∴不符合规定.
16.解:(1)∵从n边形的一个顶点可以作(n﹣3)条对角线,
∴得出把三角形分割成的三角形个数为:n﹣3+1=n﹣2,
∵这(n﹣2)个三角形的内角和都等于180°,
∴n边形的内角和是(n﹣2)×180°;
(2)设多边形的一个外角为α°,则与其相邻的内角为(3α+20)°,
由题意,得(3α+20)+α=180,
解得α=40,
即多边形的每个外角为40°,
∵多边形的外角和为360°,
∴多边形的边数为360°÷40°=9,
内角和为(9﹣2)×180°=1260°,
答:这个多边形的内角和为1260°;
(3)设多边形的边数为n,多加的外角度数为α,则
(n﹣2) 180°=1180°﹣α,
∵1180°=6×180°+100°,内角和应是180°的倍数,
∴小明多加的一个外角为100°,
∴这是6+2=8边形的内角和.
答:这个外角的度数是100°,该多边形的边数是8.
