人教版八年级数学上册12.3角的平分线的性质同步达标测试题 (含解析)
文档属性
| 名称 | 人教版八年级数学上册12.3角的平分线的性质同步达标测试题 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 495.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 21:50:17 | ||
图片预览


文档简介
2022-2023学年人教版八年级数学上册《12.3角的平分线的性质》同步达标测试题(附答案)
一.选择题(共10小题,满分40分)
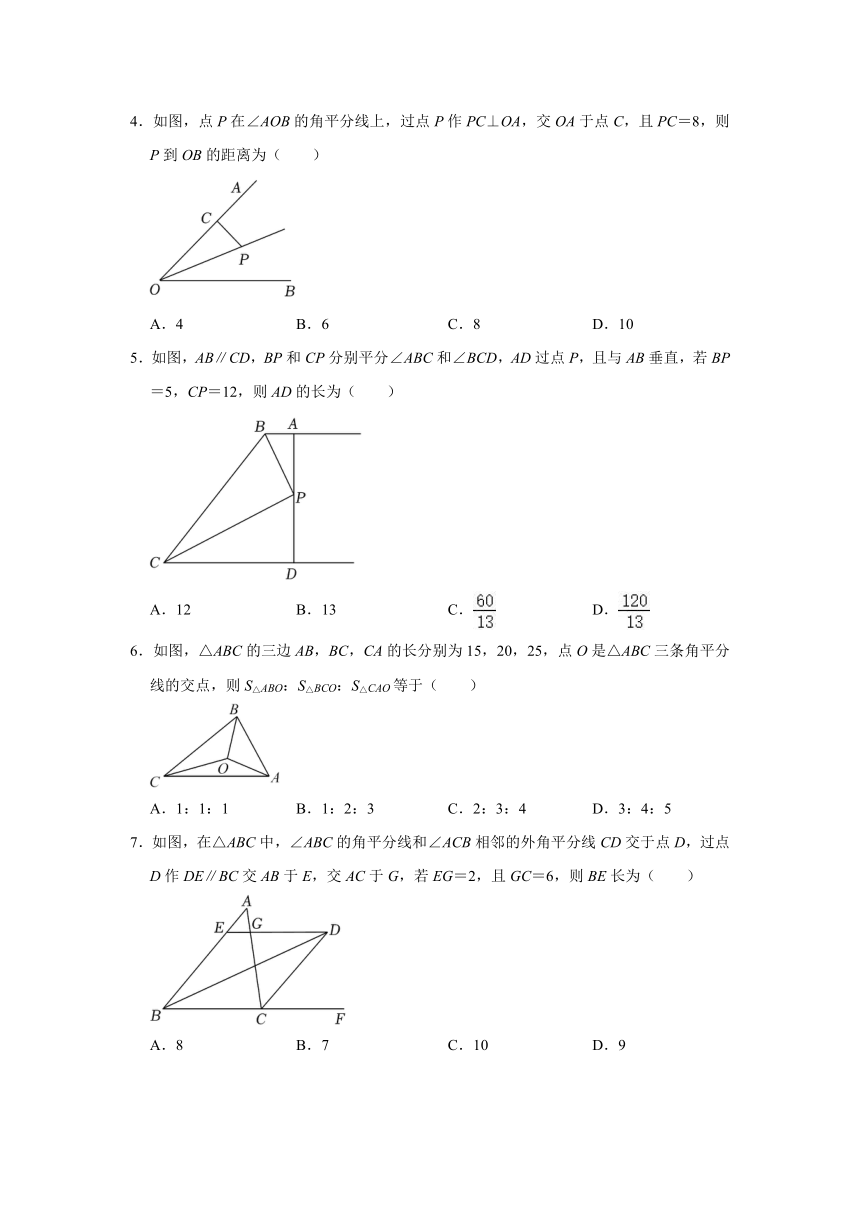
1.如图,Rt△ABC中,∠C=90°,∠B=30°,要求用圆规和直尺作图,把它分成两个三角形,其中一个三角形是等腰三角形.其作法错误的是( )
A. B.
C. D.
2.如图,点O在△ABC内,且到三边的距离相等,连接OB、OC,若∠BOC=120°,则∠A的度数是( )
A.30° B.60° C.45° D.70°
3.如图,在直角三角形ABC中,AD为斜边上的高,AE是角平分线,AF是中线,则下列说法中错误的是( )
A.BF=CF B.∠C=∠BAD
C.∠BAE=∠CAE D.S△ABE=S△ACF
4.如图,点P在∠AOB的角平分线上,过点P作PC⊥OA,交OA于点C,且PC=8,则P到OB的距离为( )
A.4 B.6 C.8 D.10
5.如图,AB∥CD,BP和CP分别平分∠ABC和∠BCD,AD过点P,且与AB垂直,若BP=5,CP=12,则AD的长为( )
A.12 B.13 C. D.
6.如图,△ABC的三边AB,BC,CA的长分别为15,20,25,点O是△ABC三条角平分线的交点,则S△ABO:S△BCO:S△CAO等于( )
A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:5
7.如图,在△ABC中,∠ABC的角平分线和∠ACB相邻的外角平分线CD交于点D,过点D作DE∥BC交AB于E,交AC于G,若EG=2,且GC=6,则BE长为( )
A.8 B.7 C.10 D.9
8.如图:已知∠ABC=∠ACB=50°,BD、CD、BE分别平分△ABC的内角∠ABC、外角∠ACP、外角∠MBC,其中点D、C、E在同一条直线上,以下结论:错误的是( )
A.∠DCP=65° B.∠BDC=40° C.∠DBE=85° D.∠E=50°
9.如图,在△ABC中,∠BAC=90°,AD是BC边上的高,BE是AC边的中线,CF是∠ACB的角平分线,CF交AD于点G,交BE于点H,下面说法正确的是( )
①△ABE的面积=△BCE的面积;②∠FAG=∠FCB;③AF=AG;④BH=CH.
A.①②③④ B.①②③ C.②④ D.①③
10.如图,在△ABC中,∠BAC=90°,高AD与角平分线BE相交于点F,∠DAC的平分线AG分别交BC、BE于点G、O,连接FG,下列结论:①∠ABD=∠DAC;②∠AFE=∠AEF;③AG⊥EF;④FG∥AC,其中所有正确结论的序号是( )
A.①② B.①③ C.①②③ D.①②③④
二.填空题(共8小题,满分32分)
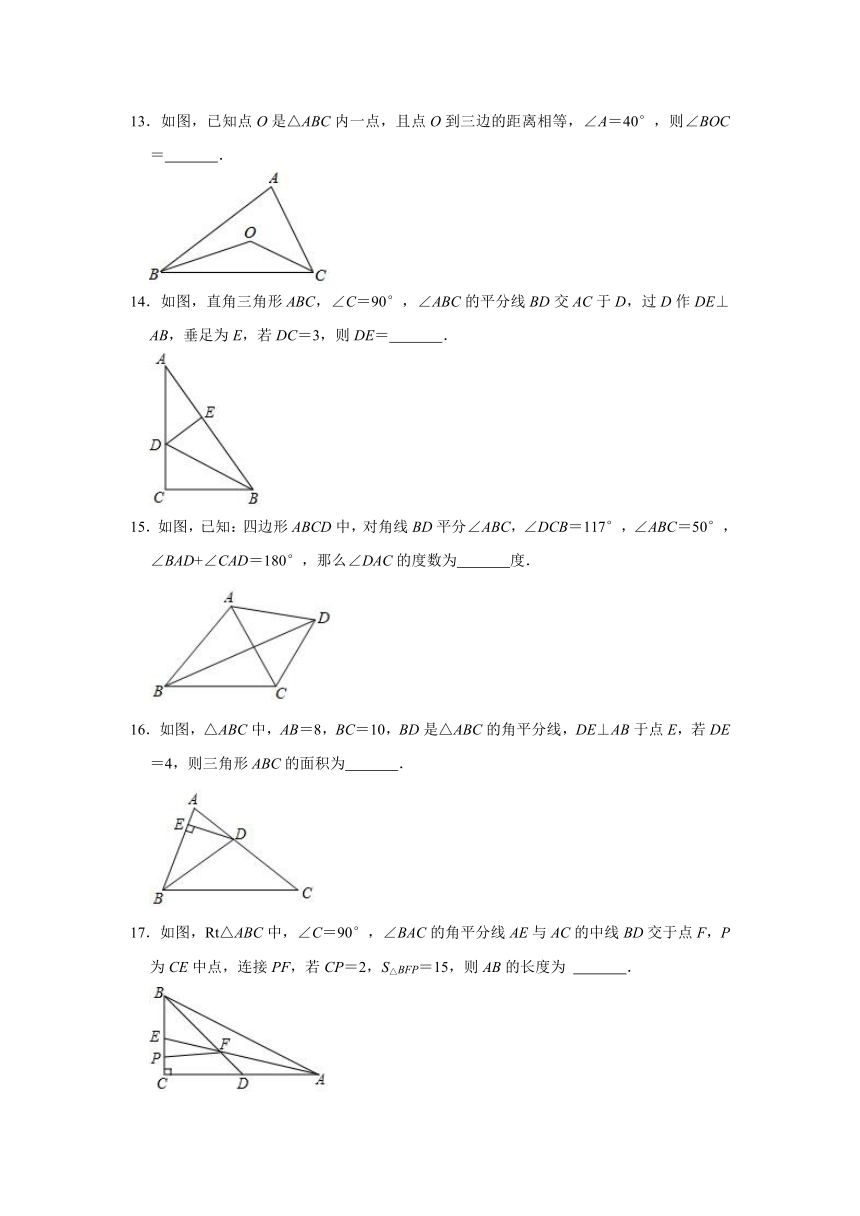
11.AD是△ABC中∠BAC的平分线,DE⊥AB于点E,若S△ABC=10,DE=2,AB=4,则AC的长是 .
12.如图,∠C=90°,∠1=∠2,若BC=10,BD=6,则D到AB的距离为 .
13.如图,已知点O是△ABC内一点,且点O到三边的距离相等,∠A=40°,则∠BOC= .
14.如图,直角三角形ABC,∠C=90°,∠ABC的平分线BD交AC于D,过D作DE⊥AB,垂足为E,若DC=3,则DE= .
15.如图,已知:四边形ABCD中,对角线BD平分∠ABC,∠DCB=117°,∠ABC=50°,∠BAD+∠CAD=180°,那么∠DAC的度数为 度.
16.如图,△ABC中,AB=8,BC=10,BD是△ABC的角平分线,DE⊥AB于点E,若DE=4,则三角形ABC的面积为 .
17.如图,Rt△ABC中,∠C=90°,∠BAC的角平分线AE与AC的中线BD交于点F,P为CE中点,连接PF,若CP=2,S△BFP=15,则AB的长度为 .
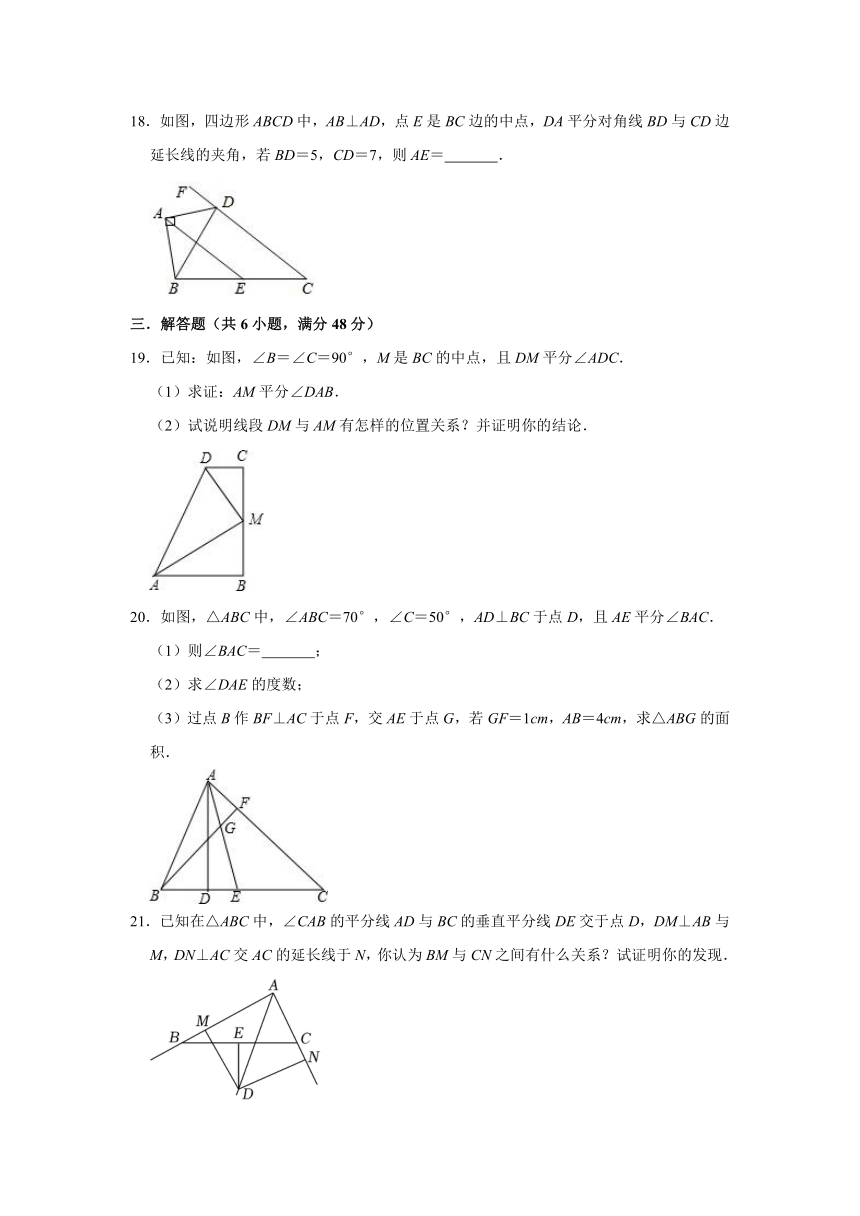
18.如图,四边形ABCD中,AB⊥AD,点E是BC边的中点,DA平分对角线BD与CD边延长线的夹角,若BD=5,CD=7,则AE= .
三.解答题(共6小题,满分48分)
19.已知:如图,∠B=∠C=90°,M是BC的中点,且DM平分∠ADC.
(1)求证:AM平分∠DAB.
(2)试说明线段DM与AM有怎样的位置关系?并证明你的结论.
20.如图,△ABC中,∠ABC=70°,∠C=50°,AD⊥BC于点D,且AE平分∠BAC.
(1)则∠BAC= ;
(2)求∠DAE的度数;
(3)过点B作BF⊥AC于点F,交AE于点G,若GF=1cm,AB=4cm,求△ABG的面积.
21.已知在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB与M,DN⊥AC交AC的延长线于N,你认为BM与CN之间有什么关系?试证明你的发现.
22.已知:∠DAB=120°,AC平分∠DAB,∠B+∠D=180°.
(1)如图1,当∠B=∠D时,求证:AB+AD=AC;
(2)如图2,当∠B≠∠D时,猜想(1)中的结论是否发生改变并说明理由.
23.在△ABC中,AC=BC,∠C=90°,点D是线段BC上一点,以AD为腰在AD右边作等腰△ADE,AD=AE.
(1)如图1,若AD平分∠BAC,且CD=1,求AB的长度;
(2)如图2,当∠EDC=∠BAD,连接BE交AC于点F,求证:BD=2CF.
24.如图①,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形.请你参考这个作全等三角形的方法,解答下列问题:
(1)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你判断并写出FE与FD之间的数量关系;(不需证明)
(2)如图③,在△ABC中,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F,请问,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
参考答案
一.选择题(共10小题,满分40分)
1.解:A.由作法知AD=AC,
∴△ACD是等腰三角形,故选项A不符合题意;
B.由作法知所作图形是线段BC的垂直平分线,
∴不能推出△ACD和△ABD是等腰三角形,故选项B符合题意;
C由作法知,所作图形是线段AB的垂直平分线,
∴DA=DB,
∴△ABD是等腰三角形,故选项C不符合题意;
D.∠C=90°,∠B=30°,
∠BAC=60°,
由作法知AD是∠BAC的平分线,
∴∠BAD=30°=∠B,
∴DB=DA,
∴△ABD是等腰三角形,故选项D不符合题意;
故选B.
2.解:∵点O在△ABC内,且到三边的距离相等,
∴OB平分∠ABC,OC平分∠ACB,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∵∠OBC+∠OCB=180°﹣∠BOC=180°﹣120°=60°,
∴∠ABC+∠ACB=2(∠OBC+∠OCB)=2×60°=120°,
∴∠A=180°﹣∠ABC﹣∠ACB=60°.
故选:B.
3.解:∵AF为斜边BC的中线,
∴BF=CF=AF,所以A选项不符合题意;
∵AD为斜边上的高,
∴∠ADB=90°,
∵∠BAD+∠B=90°,∠C+∠B=90°,
∴∠C=∠BAD,所以B选项不符合题意;
∵AE是△ABC的角平分线,
∴∠BAE=∠CAE,所以C选项不符合题意;
∵BF=CF,
∴S△ABF=S△ACF,所以D选项符合题意.
故选:D.
4.解:过P点作PD⊥OB于D,如图,
∵点P在∠AOB的角平分线上,PC⊥OA,
∴PD=PC=8,
即P到OB的距离为8.
故选:C.
5.解:过P点作PH⊥BC于H,如图,
∵AB∥CD,AD⊥AB,
∴AD⊥CD,∠ABC+∠DCB=180°,
∵BP和CP分别平分∠ABC和∠BCD,
∴PH=PA=PD,∠PCB=∠DCB,∠PBC=∠ABC,
∴∠PBC+∠PCB=(∠ABC+∠DCB)=×180°=90°,
∴∠BPC=90°,
∴BC=13,
∵PH BC=PB PC,
∴PH==,
∴PA=PD=PH=,
∴AD=2PA=.
故选:D.
6.解:过O点作OD⊥AB于D,OE⊥BC于E,OF⊥CA于F,如图,
∵点O是△ABC三条角平分线的交点,
∴OD=OE=OF,
∴S△ABO:S△BCO:S△CAO=(AB OD):(OE BC):(OF AC)=AB:BC:AC=15:20:25=3:4:5.
故选:D.
7.解:∵CD平分∠ACF,
∴∠ACD=∠FCD,
∵DE∥BF,
∴∠FCD=∠EDC,
∴∠ACD=∠EDC,
∴GD=GC=6,
∵BD平分∠ABC,
∴∠ABD=∠FBD,
∵DE∥BF,
∴∠FBD=∠EDB,
∴∠ABD=∠EDB,
∴BE=DE=EG+DG=2+6=8.
故选:A.
8.解:∵∠ACB=50°,
∴∠ACP=180°﹣∠ACB=130°,
∵CD平分∠ACP,
∴∠DCP=∠ACP=×130°=65°,所以A选项不符合题意;
∵∠ABC=50°,BD平分∠ABC,
∴∠DBC=×50°=25°,
∵∠DCP=∠BDC+∠DBC,
∴∠BDC=∠DCP﹣∠DBC=65°﹣25°=40°,所以B选项不符合题意;
∵∠CBM+∠ABC=180°,
∴∠CBM=180°﹣50°=130°,
∵BE平分∠MBC,
∴∠CBE=∠CBM=65°,
∴∠DBE=∠DBC+∠CBE=25°+65°=90°,所以C选项符合题意;
∵∠BCE=∠DCP=65°,
∴∠E=180°﹣∠CBE﹣∠BCE=180°﹣65°﹣65°=50°,所以D选项不符合题意.
故选:C.
9.解:∵BE是AC边的中线,
∴AE=CE,
∵△ABE的面积=,△BCE的面积=AB,
∴△ABE的面积=△BCE的面积,故①正确;
∵AD是BC边上的高,
∴∠ADC=90°,
∵∠BAC=90°,
∴∠DAC+∠ACB=90°,∠FAG+∠DAC=90°,
∴∠FAG=∠ACB,
∵CF是∠ACB的角平分线,
∴∠ACF=∠FCB,∠ACB=2∠FCB,
∴∠FAG=2∠FCB,故②错误;
∵在△ACF和△DGC中,∠BAC=∠ADC=90°,∠ACF=∠FCB,
∴∠AFG=180°﹣∠BAC﹣∠ACF,∠AGF=∠DGC=180°﹣∠ADC﹣∠FCB,
∴∠AFG=∠AGF,
∴AF=AG,故③正确;
根据已知不能推出∠HBC=∠HCB,即不能推出HB=HC,故④错误;
即正确的为①③,
故选:D.
10.解:∵AD为高,
∴∠ADB=90°,
∵∠BAD+∠ABD=90°,∠BAD+∠DAC=90°,
∴∠ABD=∠DAC,所以①正确;
∵∠ABD+∠C=90°,
∴∠BAD=∠C,
∵∠AFE=∠ABF+∠BAF,∠AEF=∠C+∠EAC,
∴∠AFE=∠AEF,所以②正确;
∵AG平分∠DAC,
∵∠FAO=∠EAO,
∵∠AFE+∠AFE+∠FAE=180°,
∴∠AFO+∠FAO=90°,
∴AO⊥EF,所以③正确;
∵BO⊥AG,AD⊥BG,
∴F点为△ABG三条高的交点,
∴GF⊥AB,
而CA⊥BA,
∴FG∥AC,所以④正确.
故选:D.
二.填空题(共8小题,满分32分)
11.解:作DF⊥AC交AC于点F,
∵AD是△ABC中∠BAC的平分线,DE⊥AB于点E,DF⊥AC交AC于点F,
∴DF=DE=2.
又∵S△ABC=S△ABD+S△ACD,AB=4,
∴10=×4×2+×AC×2,
∴AC=6.
故答案为:6
12.解:∵BC=10,BD=6,
∴CD=4,
∵∠C=90°,∠1=∠2,
∴点D到边AB的距离等于CD=4,
故答案为:4.
13.解:∵∠A=40°,
∴∠ABC+∠ACB=140°,
∵点O到△ABC三边的距离相等,
∴BO平分∠ABC,CO平分∠ACB,
∴∠OBC+∠OCB=×(∠ABC+∠ACB)=70°,
∴∠BOC=180°﹣70°=110°,
故答案为:110°.
14.解:∵BD是∠ABC的平分线,DE⊥AB,∠C=90°,
∴DE=DC=3,
故答案为:3.
15.解:如图,延长BA和BC,过D点作DE⊥BA于E点,过D点作DF⊥BC于F点,过D点作DG⊥AC于G点,
又∵BD是∠ABC的平分线,
∴DE=DF,
又∵∠BAD+∠CAD=180°,∠BAD+∠EAD=180°,
∴∠CAD=∠EAD,
∴AD为∠EAC的平分线,
∴DE=DG,
∴DG=DF.
∴CD为∠ACF的平分线,
∵∠DCB=117°,
∴∠DCF=63°,
∴∠ACF=126°,
∴∠BAC=∠ACF﹣∠ABC=126°﹣50°=76°,
∴∠CAE=104°,
∴∠CAD=×104°=52°,
故答案为:52.
16.解:过D作DF⊥BC,
∵BD是△ABC的角平分线,DE⊥AB于点E,DE=4,
∴DF=4,
∴△ABC的面积=△ABD的面积+△DBC的面积=
,
故答案为:36
17.解:过E作EG⊥AB于G,连接CF,
∵P为CE中点,
∵S△EFP=S△CFP,
设S△EFP=S△CFP=y,
∵BD是AC边上的中线,
∴设S△CDF=S△AFD=z,
∵S△BFP=15,
∴S△BCD=15+y+z,
∴S△ABC=2S△BCD=30+2y+2z,
∵S△ACE=S△ACF+S△CEF=2y+2z,
∴S△ABE=S△ABC﹣S△ACE=30+2y+2z﹣(2y+2z)=30,
∵AE是∠CAB的角平分线,
∴EG=CE=2CP=4,
∴S△ABE=AB EG=30,
∴AB=15,
故答案为:15.
18.解:方法一,如图,
取BD中点H,连AH、EH,
∵AB⊥AD,
∴AH=DH=BH=BD=2.5,
∴∠HDA=∠HAD,
∵DA平分∠FDB,
∴∠FDA=∠HDA,
∴∠FDA=∠HAD,
∴AH∥DF,
∵点E是BC边的中点,点H是BD的中点,
∴EH∥CD,EH=CD=3.5,
∴A、H、E三点共线,
∴AE=AH+EH=2.5+3.5=6.
方法二,如图,延长BA和CD交于一点G,
证明三角形BDA和三角形GDA全等,
得A是BG中点,
则AE是中位线,
AE等于CG的一半
故答案为:6.
三.解答题(共6小题,满分48分)
19.(1)证明:过M作ME⊥AD于E,
∵DM平分∠ADC,∠C=90°,ME⊥AD,
∴MC=ME,
∵M为BC的中点,
∴BM=MC=ME,
∵∠B=90°,ME⊥AD,
∴AM平分∠DAB;
(2)AM⊥DM,
证明如下:
∵AB∥DC,
∴∠BAD+∠ADC=180°,
∵AM平分∠DAB,DM平分∠ADC,
∴∠MAD=∠BAD,∠MDA=∠ADC,
∴∠MAD+∠MDA=90°,
∴∠AMD=90°,
∴AM⊥DM.
20.解:(1)∵∠ABC=70°,∠C=50°,
∴∠BAC=180°﹣70°﹣50°=60°,
故答案为:60°;
(2)∵AE平分∠BAC,
∴∠BAE=∠BAC=30°,
∵AD⊥BC,∠ABC=70°,
∴∠BAD=20°,
∴∠DAE=10°;
(3)作GH⊥AB于H,
∵AE平分∠BAC,GH⊥AB,BF⊥AC,
∴GH=GF=1cm,又AB=4cm,
∴△ABG的面积=×AB×GH=2cm2.
21.解:BM=CN.
理由:连接BD,CD,
∵AD平分∠BAC,DM⊥AB,DN⊥AC,
∴DM=DN,
∵DE垂直平分BC,
∴BD=CD,
在Rt△BMD与Rt△CND中
∵
∴Rt△BDM≌Rt△CDN(HL),
∴BM=CN.
22.(1)证明:∵∠B=∠D,∠B+∠D=180°,
∴∠B=∠D=90°,
∵∠DAB=120°,AC平分∠DAB,
∴∠DAC=∠BAC=60°,
∴∠ACD=∠ACB=90°﹣60°=30°,
∴AC=2AD,AC=2AB,
∴2AB+2AD=2AC,
∴AB+AD=AC;
(2)猜想:不会改变.
理由如下:过点C作CE⊥AD,CF⊥AB,垂足分别为E、F,
根据(1)的结论,AB+AD=AC,
∵AC平分∠DAB,
∴CE=CF,
∵∠B+∠D=180°,∠ABC+∠CBF=180°,
∴∠D=∠CBF,
在△CDE与△CBF中,,
∴△CDE≌△CBF(AAS),
∴DE=BF,
∴AD+AB=AE+DE+AB=AE+BF+AB=AE+AF,
∴AD+AB=AC.
即(1)中的结论没有发生改变.
23.(1)解:如图1中,过点D作DH⊥AB于H.
∴CA=CB,∠ACB=90°,
∴∠B=45°,
∴AD平分∠BAC,DH⊥AB,DC⊥AC,
∴DH=DC=1,
∴BD=DH=,
∴AC=BC=+1,
∴AB=AC=2+.
(2)证明:如图2中,延长BC到T,使得CT=CB,连接AT,ET.
∵CB=CT,AC⊥BT,
∴AB=AT,
∴∠ABT=∠ATB=45°,
∵∠BAD=∠EDC,∠ADT=∠ABD+∠BAD,
∴∠ADE=∠ABD=45°,
∵AD=AE,
∴∠ADE=∠AED=45°,
∴∠BAT=∠DAE=90°,
∴∠BAD=∠TAE,
∵AB=AT,AD=AE,
∴△BAD≌△TAE(ASA),
∴∠ABD=∠ATE=45°,BD=ET,
∴∠BTE=∠ATB+∠ATE=90°,
∴∠BCF=∠BTE=90°,
∴CF∥ET,
∵BC=CT,
∴BF=FE,
∴ET=2CF,
∴BD=2CF.
24.解:图①如图所示;
(1)FE=FD;
(2)如图,过点F作FG⊥AB于G,作FH⊥BC于H,作FK⊥AC于K,
∵AD、CE分别是∠BAC、∠BCA的平分线,
∴FG=FH=FK,
在四边形BGFH中,∠GFH=360°﹣60°﹣90°×2=120°,
∵AD、CE分别是∠BAC、∠BCA的平分线,∠B=60°,
∴∠FAC+∠FCA=(180°﹣60°)=60°,
在△AFC中,∠AFC=180°﹣(∠FAC+∠FCA)=180°﹣60°=120°,
∴∠EFD=∠AFC=120°,
∴∠EFG=∠DFH,
在△EFG和△DFH中,
,
∴△EFG≌△DFH(ASA),
∴FE=FD.
一.选择题(共10小题,满分40分)
1.如图,Rt△ABC中,∠C=90°,∠B=30°,要求用圆规和直尺作图,把它分成两个三角形,其中一个三角形是等腰三角形.其作法错误的是( )
A. B.
C. D.
2.如图,点O在△ABC内,且到三边的距离相等,连接OB、OC,若∠BOC=120°,则∠A的度数是( )
A.30° B.60° C.45° D.70°
3.如图,在直角三角形ABC中,AD为斜边上的高,AE是角平分线,AF是中线,则下列说法中错误的是( )
A.BF=CF B.∠C=∠BAD
C.∠BAE=∠CAE D.S△ABE=S△ACF
4.如图,点P在∠AOB的角平分线上,过点P作PC⊥OA,交OA于点C,且PC=8,则P到OB的距离为( )
A.4 B.6 C.8 D.10
5.如图,AB∥CD,BP和CP分别平分∠ABC和∠BCD,AD过点P,且与AB垂直,若BP=5,CP=12,则AD的长为( )
A.12 B.13 C. D.
6.如图,△ABC的三边AB,BC,CA的长分别为15,20,25,点O是△ABC三条角平分线的交点,则S△ABO:S△BCO:S△CAO等于( )
A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:5
7.如图,在△ABC中,∠ABC的角平分线和∠ACB相邻的外角平分线CD交于点D,过点D作DE∥BC交AB于E,交AC于G,若EG=2,且GC=6,则BE长为( )
A.8 B.7 C.10 D.9
8.如图:已知∠ABC=∠ACB=50°,BD、CD、BE分别平分△ABC的内角∠ABC、外角∠ACP、外角∠MBC,其中点D、C、E在同一条直线上,以下结论:错误的是( )
A.∠DCP=65° B.∠BDC=40° C.∠DBE=85° D.∠E=50°
9.如图,在△ABC中,∠BAC=90°,AD是BC边上的高,BE是AC边的中线,CF是∠ACB的角平分线,CF交AD于点G,交BE于点H,下面说法正确的是( )
①△ABE的面积=△BCE的面积;②∠FAG=∠FCB;③AF=AG;④BH=CH.
A.①②③④ B.①②③ C.②④ D.①③
10.如图,在△ABC中,∠BAC=90°,高AD与角平分线BE相交于点F,∠DAC的平分线AG分别交BC、BE于点G、O,连接FG,下列结论:①∠ABD=∠DAC;②∠AFE=∠AEF;③AG⊥EF;④FG∥AC,其中所有正确结论的序号是( )
A.①② B.①③ C.①②③ D.①②③④
二.填空题(共8小题,满分32分)
11.AD是△ABC中∠BAC的平分线,DE⊥AB于点E,若S△ABC=10,DE=2,AB=4,则AC的长是 .
12.如图,∠C=90°,∠1=∠2,若BC=10,BD=6,则D到AB的距离为 .
13.如图,已知点O是△ABC内一点,且点O到三边的距离相等,∠A=40°,则∠BOC= .
14.如图,直角三角形ABC,∠C=90°,∠ABC的平分线BD交AC于D,过D作DE⊥AB,垂足为E,若DC=3,则DE= .
15.如图,已知:四边形ABCD中,对角线BD平分∠ABC,∠DCB=117°,∠ABC=50°,∠BAD+∠CAD=180°,那么∠DAC的度数为 度.
16.如图,△ABC中,AB=8,BC=10,BD是△ABC的角平分线,DE⊥AB于点E,若DE=4,则三角形ABC的面积为 .
17.如图,Rt△ABC中,∠C=90°,∠BAC的角平分线AE与AC的中线BD交于点F,P为CE中点,连接PF,若CP=2,S△BFP=15,则AB的长度为 .
18.如图,四边形ABCD中,AB⊥AD,点E是BC边的中点,DA平分对角线BD与CD边延长线的夹角,若BD=5,CD=7,则AE= .
三.解答题(共6小题,满分48分)
19.已知:如图,∠B=∠C=90°,M是BC的中点,且DM平分∠ADC.
(1)求证:AM平分∠DAB.
(2)试说明线段DM与AM有怎样的位置关系?并证明你的结论.
20.如图,△ABC中,∠ABC=70°,∠C=50°,AD⊥BC于点D,且AE平分∠BAC.
(1)则∠BAC= ;
(2)求∠DAE的度数;
(3)过点B作BF⊥AC于点F,交AE于点G,若GF=1cm,AB=4cm,求△ABG的面积.
21.已知在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB与M,DN⊥AC交AC的延长线于N,你认为BM与CN之间有什么关系?试证明你的发现.
22.已知:∠DAB=120°,AC平分∠DAB,∠B+∠D=180°.
(1)如图1,当∠B=∠D时,求证:AB+AD=AC;
(2)如图2,当∠B≠∠D时,猜想(1)中的结论是否发生改变并说明理由.
23.在△ABC中,AC=BC,∠C=90°,点D是线段BC上一点,以AD为腰在AD右边作等腰△ADE,AD=AE.
(1)如图1,若AD平分∠BAC,且CD=1,求AB的长度;
(2)如图2,当∠EDC=∠BAD,连接BE交AC于点F,求证:BD=2CF.
24.如图①,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形.请你参考这个作全等三角形的方法,解答下列问题:
(1)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你判断并写出FE与FD之间的数量关系;(不需证明)
(2)如图③,在△ABC中,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F,请问,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
参考答案
一.选择题(共10小题,满分40分)
1.解:A.由作法知AD=AC,
∴△ACD是等腰三角形,故选项A不符合题意;
B.由作法知所作图形是线段BC的垂直平分线,
∴不能推出△ACD和△ABD是等腰三角形,故选项B符合题意;
C由作法知,所作图形是线段AB的垂直平分线,
∴DA=DB,
∴△ABD是等腰三角形,故选项C不符合题意;
D.∠C=90°,∠B=30°,
∠BAC=60°,
由作法知AD是∠BAC的平分线,
∴∠BAD=30°=∠B,
∴DB=DA,
∴△ABD是等腰三角形,故选项D不符合题意;
故选B.
2.解:∵点O在△ABC内,且到三边的距离相等,
∴OB平分∠ABC,OC平分∠ACB,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∵∠OBC+∠OCB=180°﹣∠BOC=180°﹣120°=60°,
∴∠ABC+∠ACB=2(∠OBC+∠OCB)=2×60°=120°,
∴∠A=180°﹣∠ABC﹣∠ACB=60°.
故选:B.
3.解:∵AF为斜边BC的中线,
∴BF=CF=AF,所以A选项不符合题意;
∵AD为斜边上的高,
∴∠ADB=90°,
∵∠BAD+∠B=90°,∠C+∠B=90°,
∴∠C=∠BAD,所以B选项不符合题意;
∵AE是△ABC的角平分线,
∴∠BAE=∠CAE,所以C选项不符合题意;
∵BF=CF,
∴S△ABF=S△ACF,所以D选项符合题意.
故选:D.
4.解:过P点作PD⊥OB于D,如图,
∵点P在∠AOB的角平分线上,PC⊥OA,
∴PD=PC=8,
即P到OB的距离为8.
故选:C.
5.解:过P点作PH⊥BC于H,如图,
∵AB∥CD,AD⊥AB,
∴AD⊥CD,∠ABC+∠DCB=180°,
∵BP和CP分别平分∠ABC和∠BCD,
∴PH=PA=PD,∠PCB=∠DCB,∠PBC=∠ABC,
∴∠PBC+∠PCB=(∠ABC+∠DCB)=×180°=90°,
∴∠BPC=90°,
∴BC=13,
∵PH BC=PB PC,
∴PH==,
∴PA=PD=PH=,
∴AD=2PA=.
故选:D.
6.解:过O点作OD⊥AB于D,OE⊥BC于E,OF⊥CA于F,如图,
∵点O是△ABC三条角平分线的交点,
∴OD=OE=OF,
∴S△ABO:S△BCO:S△CAO=(AB OD):(OE BC):(OF AC)=AB:BC:AC=15:20:25=3:4:5.
故选:D.
7.解:∵CD平分∠ACF,
∴∠ACD=∠FCD,
∵DE∥BF,
∴∠FCD=∠EDC,
∴∠ACD=∠EDC,
∴GD=GC=6,
∵BD平分∠ABC,
∴∠ABD=∠FBD,
∵DE∥BF,
∴∠FBD=∠EDB,
∴∠ABD=∠EDB,
∴BE=DE=EG+DG=2+6=8.
故选:A.
8.解:∵∠ACB=50°,
∴∠ACP=180°﹣∠ACB=130°,
∵CD平分∠ACP,
∴∠DCP=∠ACP=×130°=65°,所以A选项不符合题意;
∵∠ABC=50°,BD平分∠ABC,
∴∠DBC=×50°=25°,
∵∠DCP=∠BDC+∠DBC,
∴∠BDC=∠DCP﹣∠DBC=65°﹣25°=40°,所以B选项不符合题意;
∵∠CBM+∠ABC=180°,
∴∠CBM=180°﹣50°=130°,
∵BE平分∠MBC,
∴∠CBE=∠CBM=65°,
∴∠DBE=∠DBC+∠CBE=25°+65°=90°,所以C选项符合题意;
∵∠BCE=∠DCP=65°,
∴∠E=180°﹣∠CBE﹣∠BCE=180°﹣65°﹣65°=50°,所以D选项不符合题意.
故选:C.
9.解:∵BE是AC边的中线,
∴AE=CE,
∵△ABE的面积=,△BCE的面积=AB,
∴△ABE的面积=△BCE的面积,故①正确;
∵AD是BC边上的高,
∴∠ADC=90°,
∵∠BAC=90°,
∴∠DAC+∠ACB=90°,∠FAG+∠DAC=90°,
∴∠FAG=∠ACB,
∵CF是∠ACB的角平分线,
∴∠ACF=∠FCB,∠ACB=2∠FCB,
∴∠FAG=2∠FCB,故②错误;
∵在△ACF和△DGC中,∠BAC=∠ADC=90°,∠ACF=∠FCB,
∴∠AFG=180°﹣∠BAC﹣∠ACF,∠AGF=∠DGC=180°﹣∠ADC﹣∠FCB,
∴∠AFG=∠AGF,
∴AF=AG,故③正确;
根据已知不能推出∠HBC=∠HCB,即不能推出HB=HC,故④错误;
即正确的为①③,
故选:D.
10.解:∵AD为高,
∴∠ADB=90°,
∵∠BAD+∠ABD=90°,∠BAD+∠DAC=90°,
∴∠ABD=∠DAC,所以①正确;
∵∠ABD+∠C=90°,
∴∠BAD=∠C,
∵∠AFE=∠ABF+∠BAF,∠AEF=∠C+∠EAC,
∴∠AFE=∠AEF,所以②正确;
∵AG平分∠DAC,
∵∠FAO=∠EAO,
∵∠AFE+∠AFE+∠FAE=180°,
∴∠AFO+∠FAO=90°,
∴AO⊥EF,所以③正确;
∵BO⊥AG,AD⊥BG,
∴F点为△ABG三条高的交点,
∴GF⊥AB,
而CA⊥BA,
∴FG∥AC,所以④正确.
故选:D.
二.填空题(共8小题,满分32分)
11.解:作DF⊥AC交AC于点F,
∵AD是△ABC中∠BAC的平分线,DE⊥AB于点E,DF⊥AC交AC于点F,
∴DF=DE=2.
又∵S△ABC=S△ABD+S△ACD,AB=4,
∴10=×4×2+×AC×2,
∴AC=6.
故答案为:6
12.解:∵BC=10,BD=6,
∴CD=4,
∵∠C=90°,∠1=∠2,
∴点D到边AB的距离等于CD=4,
故答案为:4.
13.解:∵∠A=40°,
∴∠ABC+∠ACB=140°,
∵点O到△ABC三边的距离相等,
∴BO平分∠ABC,CO平分∠ACB,
∴∠OBC+∠OCB=×(∠ABC+∠ACB)=70°,
∴∠BOC=180°﹣70°=110°,
故答案为:110°.
14.解:∵BD是∠ABC的平分线,DE⊥AB,∠C=90°,
∴DE=DC=3,
故答案为:3.
15.解:如图,延长BA和BC,过D点作DE⊥BA于E点,过D点作DF⊥BC于F点,过D点作DG⊥AC于G点,
又∵BD是∠ABC的平分线,
∴DE=DF,
又∵∠BAD+∠CAD=180°,∠BAD+∠EAD=180°,
∴∠CAD=∠EAD,
∴AD为∠EAC的平分线,
∴DE=DG,
∴DG=DF.
∴CD为∠ACF的平分线,
∵∠DCB=117°,
∴∠DCF=63°,
∴∠ACF=126°,
∴∠BAC=∠ACF﹣∠ABC=126°﹣50°=76°,
∴∠CAE=104°,
∴∠CAD=×104°=52°,
故答案为:52.
16.解:过D作DF⊥BC,
∵BD是△ABC的角平分线,DE⊥AB于点E,DE=4,
∴DF=4,
∴△ABC的面积=△ABD的面积+△DBC的面积=
,
故答案为:36
17.解:过E作EG⊥AB于G,连接CF,
∵P为CE中点,
∵S△EFP=S△CFP,
设S△EFP=S△CFP=y,
∵BD是AC边上的中线,
∴设S△CDF=S△AFD=z,
∵S△BFP=15,
∴S△BCD=15+y+z,
∴S△ABC=2S△BCD=30+2y+2z,
∵S△ACE=S△ACF+S△CEF=2y+2z,
∴S△ABE=S△ABC﹣S△ACE=30+2y+2z﹣(2y+2z)=30,
∵AE是∠CAB的角平分线,
∴EG=CE=2CP=4,
∴S△ABE=AB EG=30,
∴AB=15,
故答案为:15.
18.解:方法一,如图,
取BD中点H,连AH、EH,
∵AB⊥AD,
∴AH=DH=BH=BD=2.5,
∴∠HDA=∠HAD,
∵DA平分∠FDB,
∴∠FDA=∠HDA,
∴∠FDA=∠HAD,
∴AH∥DF,
∵点E是BC边的中点,点H是BD的中点,
∴EH∥CD,EH=CD=3.5,
∴A、H、E三点共线,
∴AE=AH+EH=2.5+3.5=6.
方法二,如图,延长BA和CD交于一点G,
证明三角形BDA和三角形GDA全等,
得A是BG中点,
则AE是中位线,
AE等于CG的一半
故答案为:6.
三.解答题(共6小题,满分48分)
19.(1)证明:过M作ME⊥AD于E,
∵DM平分∠ADC,∠C=90°,ME⊥AD,
∴MC=ME,
∵M为BC的中点,
∴BM=MC=ME,
∵∠B=90°,ME⊥AD,
∴AM平分∠DAB;
(2)AM⊥DM,
证明如下:
∵AB∥DC,
∴∠BAD+∠ADC=180°,
∵AM平分∠DAB,DM平分∠ADC,
∴∠MAD=∠BAD,∠MDA=∠ADC,
∴∠MAD+∠MDA=90°,
∴∠AMD=90°,
∴AM⊥DM.
20.解:(1)∵∠ABC=70°,∠C=50°,
∴∠BAC=180°﹣70°﹣50°=60°,
故答案为:60°;
(2)∵AE平分∠BAC,
∴∠BAE=∠BAC=30°,
∵AD⊥BC,∠ABC=70°,
∴∠BAD=20°,
∴∠DAE=10°;
(3)作GH⊥AB于H,
∵AE平分∠BAC,GH⊥AB,BF⊥AC,
∴GH=GF=1cm,又AB=4cm,
∴△ABG的面积=×AB×GH=2cm2.
21.解:BM=CN.
理由:连接BD,CD,
∵AD平分∠BAC,DM⊥AB,DN⊥AC,
∴DM=DN,
∵DE垂直平分BC,
∴BD=CD,
在Rt△BMD与Rt△CND中
∵
∴Rt△BDM≌Rt△CDN(HL),
∴BM=CN.
22.(1)证明:∵∠B=∠D,∠B+∠D=180°,
∴∠B=∠D=90°,
∵∠DAB=120°,AC平分∠DAB,
∴∠DAC=∠BAC=60°,
∴∠ACD=∠ACB=90°﹣60°=30°,
∴AC=2AD,AC=2AB,
∴2AB+2AD=2AC,
∴AB+AD=AC;
(2)猜想:不会改变.
理由如下:过点C作CE⊥AD,CF⊥AB,垂足分别为E、F,
根据(1)的结论,AB+AD=AC,
∵AC平分∠DAB,
∴CE=CF,
∵∠B+∠D=180°,∠ABC+∠CBF=180°,
∴∠D=∠CBF,
在△CDE与△CBF中,,
∴△CDE≌△CBF(AAS),
∴DE=BF,
∴AD+AB=AE+DE+AB=AE+BF+AB=AE+AF,
∴AD+AB=AC.
即(1)中的结论没有发生改变.
23.(1)解:如图1中,过点D作DH⊥AB于H.
∴CA=CB,∠ACB=90°,
∴∠B=45°,
∴AD平分∠BAC,DH⊥AB,DC⊥AC,
∴DH=DC=1,
∴BD=DH=,
∴AC=BC=+1,
∴AB=AC=2+.
(2)证明:如图2中,延长BC到T,使得CT=CB,连接AT,ET.
∵CB=CT,AC⊥BT,
∴AB=AT,
∴∠ABT=∠ATB=45°,
∵∠BAD=∠EDC,∠ADT=∠ABD+∠BAD,
∴∠ADE=∠ABD=45°,
∵AD=AE,
∴∠ADE=∠AED=45°,
∴∠BAT=∠DAE=90°,
∴∠BAD=∠TAE,
∵AB=AT,AD=AE,
∴△BAD≌△TAE(ASA),
∴∠ABD=∠ATE=45°,BD=ET,
∴∠BTE=∠ATB+∠ATE=90°,
∴∠BCF=∠BTE=90°,
∴CF∥ET,
∵BC=CT,
∴BF=FE,
∴ET=2CF,
∴BD=2CF.
24.解:图①如图所示;
(1)FE=FD;
(2)如图,过点F作FG⊥AB于G,作FH⊥BC于H,作FK⊥AC于K,
∵AD、CE分别是∠BAC、∠BCA的平分线,
∴FG=FH=FK,
在四边形BGFH中,∠GFH=360°﹣60°﹣90°×2=120°,
∵AD、CE分别是∠BAC、∠BCA的平分线,∠B=60°,
∴∠FAC+∠FCA=(180°﹣60°)=60°,
在△AFC中,∠AFC=180°﹣(∠FAC+∠FCA)=180°﹣60°=120°,
∴∠EFD=∠AFC=120°,
∴∠EFG=∠DFH,
在△EFG和△DFH中,
,
∴△EFG≌△DFH(ASA),
∴FE=FD.
