人教版九年级数学上册22.1二次函数的图象和性质同步精练
文档属性
| 名称 | 人教版九年级数学上册22.1二次函数的图象和性质同步精练 |  | |
| 格式 | docx | ||
| 文件大小 | 776.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 21:41:13 | ||
图片预览



文档简介
22.1二次函数的图象和性质 同步精练
一、单选题
1.关于二次函数的最大值或最小值,下列说法正确的是( )
A.有最大值4 B.有最小值4 C.有最大值6 D.有最小值6
2.已知抛物线经过点,那么下列各点中,该抛物线必经过的点是( )
A. B. C. D.
3.在平面直角坐标系中,已知抛物线,将该抛物线沿y轴翻折所得的抛物线的表达式为( )
A. B. C. D.
4.正方形的边长为4,若边长增加x,那么面积增加y,则y关于x的函数表达式为( )
A. B. C. D.
5.把抛物线向右平移2个单位,然后向下平移1个单位,则平移后得到的抛物线解析式是( )
A. B.
C. D.
6.如图,二次函数的图象关于直线对称,与x轴交于,两点,若,则下列四个结论:①,②,③,④.
正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
7.对于抛物线,下列说法正确的是( )
A.抛物线开口向上
B.当时,y随x增大而减小
C.函数最小值为﹣2
D.顶点坐标为(1,﹣2)
8.关于二次函数,下列说法正确的是( )
A.函数图象的开口向下 B.函数图象的顶点坐标是
C.该函数有最大值,是大值是5 D.当时,y随x的增大而增大
9.已知A( 3, 2) ,B(1, 2),抛物线y=ax2+bx+c(a>0)顶点在线段AB上运动,形状保持不变,与x轴交于C,D两点(C在D的右侧),下列结论:
①c≥ 2 ;
②当x>0时,一定有y随x的增大而增大;
③若点D横坐标的最小值为 5,点C横坐标的最大值为3;
④当四边形ABCD为平行四边形时,a=.
其中正确的是( )
A.①③ B.②③ C.①④ D.①③④
10.已知二次函数(为常数,),点是该函数图象上一点,当时,,则的取值范围是( )
A.或 B.
C.或 D.
11.已知函数,则下列说法不正确的个数是( )
①若该函数图像与轴只有一个交点,则
②方程至少有一个整数根
③若,则的函数值都是负数
④不存在实数,使得对任意实数都成立
A.0 B.1 C.2 D.3
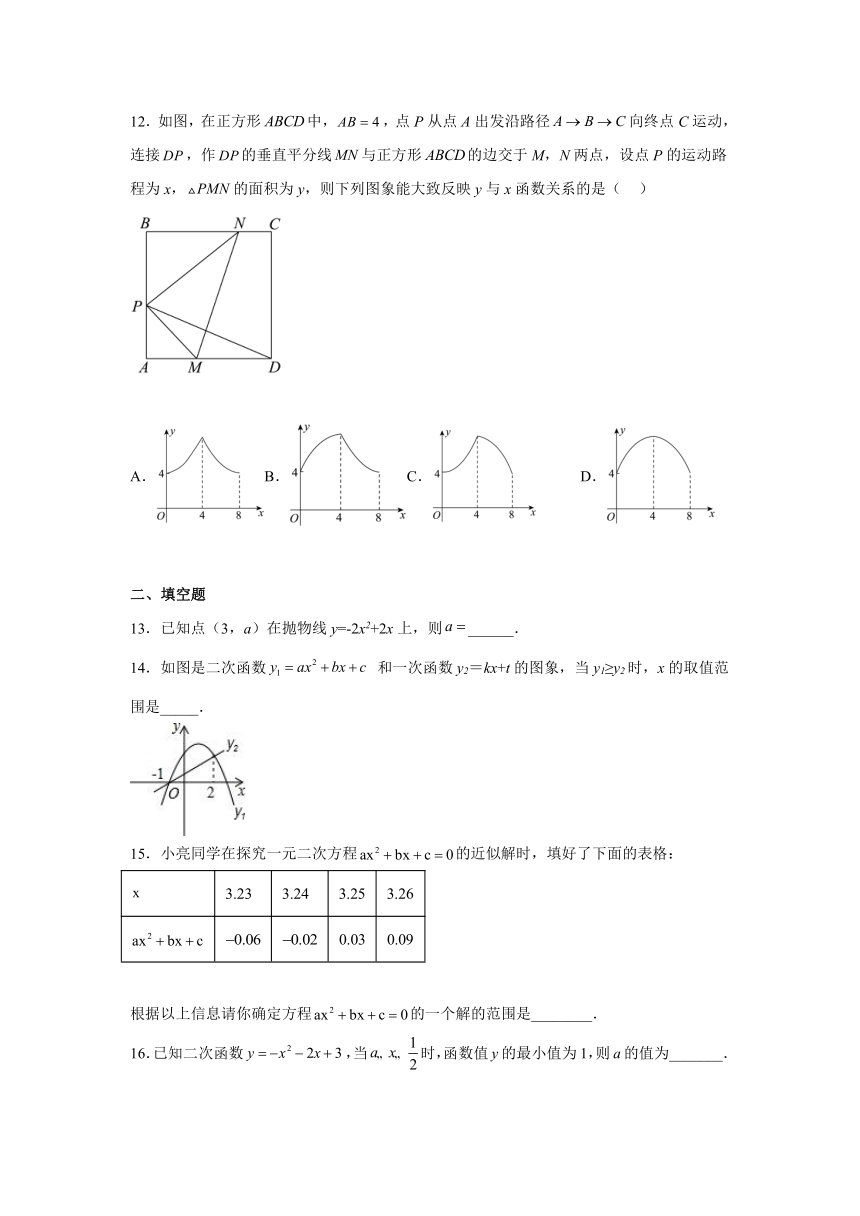
12.如图,在正方形中,,点P从点A出发沿路径向终点C运动,连接,作的垂直平分线与正方形的边交于M,N两点,设点P的运动路程为x,的面积为y,则下列图象能大致反映y与x函数关系的是( )
A.B.C. D.
二、填空题
13.已知点(3,a)在抛物线y=-2x2+2x上,则______.
14.如图是二次函数 和一次函数y2=kx+t的图象,当y1≥y2时,x的取值范围是_____.
15.小亮同学在探究一元二次方程的近似解时,填好了下面的表格:
根据以上信息请你确定方程的一个解的范围是________.
16.已知二次函数,当时,函数值y的最小值为1,则a的值为_______.
17.已知抛物线与x轴交于A,B两点,与y轴交于C点.
(1)若,则b=______.
(2)若,,抛物线与线段没有交点,则b的取值范围为______.
三、解答题
18.已知抛物线经过点,,,求该抛物线的函数关系式
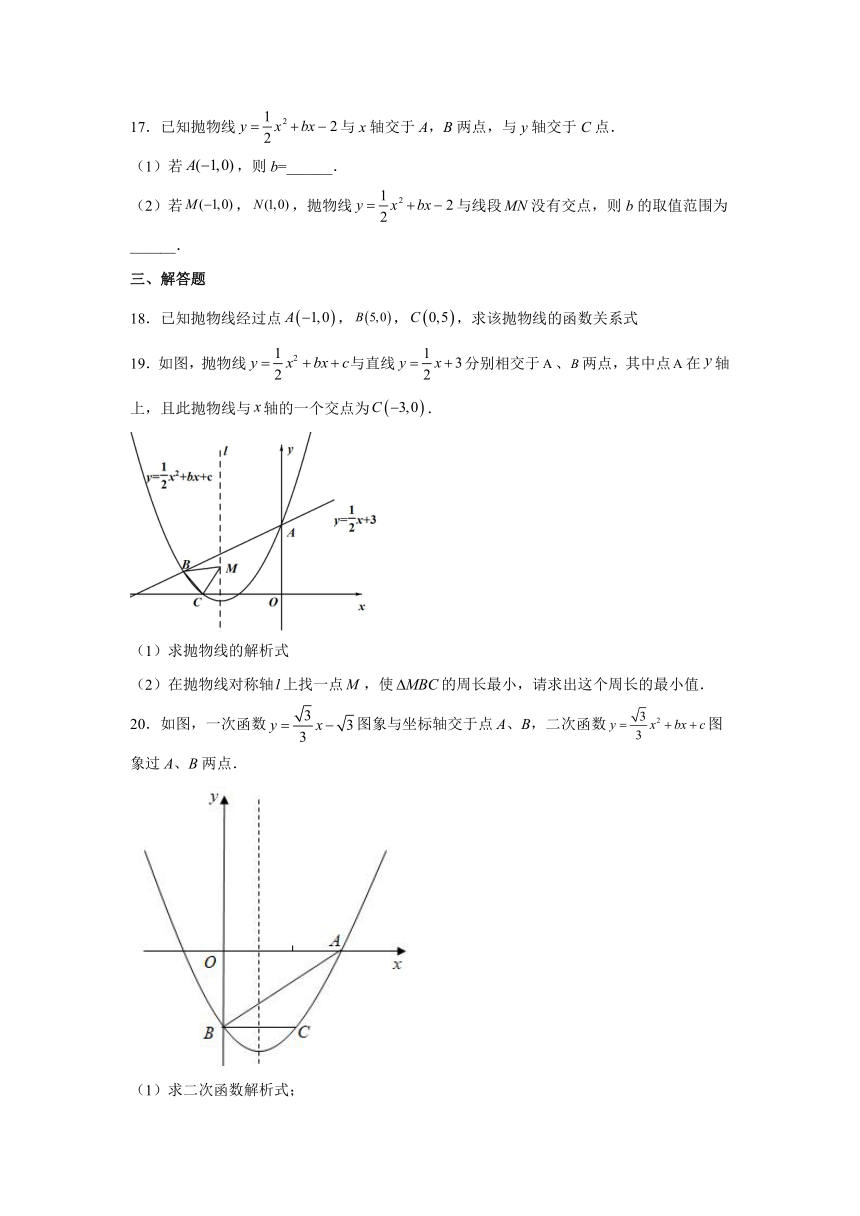
19.如图,抛物线与直线分别相交于、两点,其中点在轴上,且此抛物线与轴的一个交点为.
(1)求抛物线的解析式
(2)在抛物线对称轴上找一点,使的周长最小,请求出这个周长的最小值.
20.如图,一次函数图象与坐标轴交于点A、B,二次函数图象过A、B两点.
(1)求二次函数解析式;
(2)点B关于抛物线对称轴的对称点为点C,点P是对称轴上一动点,在抛物线上是否存在点Q,使得以B、C、P、Q为顶点的四边形是菱形?若存在,求出Q点坐标;若不存在,请说明理由.
21.如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣2,0)和点B(8,0),与y轴交于点C(0,﹣8),连接AC,D是抛物线对称轴上一动点,连接AD,CD,得到△ACD.
(1)求该抛物线的函数解析式.
(2)△ACD周长能否取得最小值,如果能,请求出D点的坐标;如果不能,请说明理由.
(3)在(2)的条件下,在抛物线上是否存在点E,使得△ACE与△ACD面积相等,如果存在,请求出点的坐标;如果不存在,请说明理由.
参考答案
1--10DBCCD BBDDA 11--12CA
13.-12
14.﹣1≤x≤2
15.
16.
17.
18.解:∵抛物线经过点,,,
∴设抛物线的表达式为,
将点代入得:,解得:,
∴.
∴该抛物线的函数关系式为.
19..解:(1)抛物线与直线交于轴上一点,
令 则
点
把,代入得:
,
解得:,
抛物线的解析式是;
(2)将直线与二次函数联立得方程组:
解得:或,
,
如图,要使的周长最小,则最小,
设二次函数与轴的另一交点为,
抛物线的对称轴为:
点,
连接 交对称轴于
,
此时,最小,
此时:,
的周长最小值为.
20.解:(1)对于:当x=0时,;
当y=0时,,妥得,x=3
∴A(3,0),B(0,)
把A(3,0),B(0,)代入得:
解得,
∴抛物线的解析式为:;
(2)抛物线的对称轴为直线
故设P(1,p),Q(m,n)
①当BC为菱形对角线时,如图,
∵B,C关于对称没对称,且对称轴与x轴垂直,
∴∴BC与对称轴垂直,且BC//x轴
∵在菱形BQCP中,BC⊥PQ
∴PQ⊥x轴
∵点P在x=1上,
∴点Q也在x=1上,
当x=1时,
∴Q(1,);
②当BC为菱形一边时,若点Q在点P右侧时,如图,
∴BC//PQ,且BC=PQ
∵BC//x轴,
∴令,则有
解得,
∴
∴PQ=BC=2
∵
∴PB=BC=2
∴迠P在x轴上,
∴P(1,0)
∴Q(3,0);
若点Q在点P的左侧,如图,
同理可得,Q(-1,0)
综上所述,Q点坐标为(1,)或(3,0)或(-1,0)
21.解:(1)由题意可得:,
解得:,
∴抛物线的解析式为:y=x2﹣3x﹣8;
(2)△ACD周长能取得最小值,
∵点A(﹣2,0),点B(8,0),
∴对称轴为直线x=3,
∵△ACD周长=AD+AC+CD,AC是定值,
∴当AD+CD取最小值时,△ACD周长能取得最小值,
∵点A,点B关于对称轴直线x=3对称,
∴连接BC交对称轴直线x=3于点D,此时AD+CD有最小值,
设直线BC解析式为:y=kx﹣8,
∴0=8k﹣8,
∴k=1,
∴直线BC解析式为:y=x﹣8,
当x=3,y=﹣5,
∴点D(3,﹣5);
(3)存在,
∵点A(﹣2,0),点C(0,﹣8),
∴直线AC解析式为y=﹣4x﹣8,
如图,
∵△ACE与△ACD面积相等,
∴DE∥AC,
∴设DE解析式为:y=﹣4x+n,
∴﹣5=﹣4×3+n,
∴n=7,
∴DE解析式为:y=﹣4x+7,
联立方程组可得:,
解得:,,
∴点E(﹣1,﹣4+11)或(﹣﹣1,4+11).
一、单选题
1.关于二次函数的最大值或最小值,下列说法正确的是( )
A.有最大值4 B.有最小值4 C.有最大值6 D.有最小值6
2.已知抛物线经过点,那么下列各点中,该抛物线必经过的点是( )
A. B. C. D.
3.在平面直角坐标系中,已知抛物线,将该抛物线沿y轴翻折所得的抛物线的表达式为( )
A. B. C. D.
4.正方形的边长为4,若边长增加x,那么面积增加y,则y关于x的函数表达式为( )
A. B. C. D.
5.把抛物线向右平移2个单位,然后向下平移1个单位,则平移后得到的抛物线解析式是( )
A. B.
C. D.
6.如图,二次函数的图象关于直线对称,与x轴交于,两点,若,则下列四个结论:①,②,③,④.
正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
7.对于抛物线,下列说法正确的是( )
A.抛物线开口向上
B.当时,y随x增大而减小
C.函数最小值为﹣2
D.顶点坐标为(1,﹣2)
8.关于二次函数,下列说法正确的是( )
A.函数图象的开口向下 B.函数图象的顶点坐标是
C.该函数有最大值,是大值是5 D.当时,y随x的增大而增大
9.已知A( 3, 2) ,B(1, 2),抛物线y=ax2+bx+c(a>0)顶点在线段AB上运动,形状保持不变,与x轴交于C,D两点(C在D的右侧),下列结论:
①c≥ 2 ;
②当x>0时,一定有y随x的增大而增大;
③若点D横坐标的最小值为 5,点C横坐标的最大值为3;
④当四边形ABCD为平行四边形时,a=.
其中正确的是( )
A.①③ B.②③ C.①④ D.①③④
10.已知二次函数(为常数,),点是该函数图象上一点,当时,,则的取值范围是( )
A.或 B.
C.或 D.
11.已知函数,则下列说法不正确的个数是( )
①若该函数图像与轴只有一个交点,则
②方程至少有一个整数根
③若,则的函数值都是负数
④不存在实数,使得对任意实数都成立
A.0 B.1 C.2 D.3
12.如图,在正方形中,,点P从点A出发沿路径向终点C运动,连接,作的垂直平分线与正方形的边交于M,N两点,设点P的运动路程为x,的面积为y,则下列图象能大致反映y与x函数关系的是( )
A.B.C. D.
二、填空题
13.已知点(3,a)在抛物线y=-2x2+2x上,则______.
14.如图是二次函数 和一次函数y2=kx+t的图象,当y1≥y2时,x的取值范围是_____.
15.小亮同学在探究一元二次方程的近似解时,填好了下面的表格:
根据以上信息请你确定方程的一个解的范围是________.
16.已知二次函数,当时,函数值y的最小值为1,则a的值为_______.
17.已知抛物线与x轴交于A,B两点,与y轴交于C点.
(1)若,则b=______.
(2)若,,抛物线与线段没有交点,则b的取值范围为______.
三、解答题
18.已知抛物线经过点,,,求该抛物线的函数关系式
19.如图,抛物线与直线分别相交于、两点,其中点在轴上,且此抛物线与轴的一个交点为.
(1)求抛物线的解析式
(2)在抛物线对称轴上找一点,使的周长最小,请求出这个周长的最小值.
20.如图,一次函数图象与坐标轴交于点A、B,二次函数图象过A、B两点.
(1)求二次函数解析式;
(2)点B关于抛物线对称轴的对称点为点C,点P是对称轴上一动点,在抛物线上是否存在点Q,使得以B、C、P、Q为顶点的四边形是菱形?若存在,求出Q点坐标;若不存在,请说明理由.
21.如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣2,0)和点B(8,0),与y轴交于点C(0,﹣8),连接AC,D是抛物线对称轴上一动点,连接AD,CD,得到△ACD.
(1)求该抛物线的函数解析式.
(2)△ACD周长能否取得最小值,如果能,请求出D点的坐标;如果不能,请说明理由.
(3)在(2)的条件下,在抛物线上是否存在点E,使得△ACE与△ACD面积相等,如果存在,请求出点的坐标;如果不存在,请说明理由.
参考答案
1--10DBCCD BBDDA 11--12CA
13.-12
14.﹣1≤x≤2
15.
16.
17.
18.解:∵抛物线经过点,,,
∴设抛物线的表达式为,
将点代入得:,解得:,
∴.
∴该抛物线的函数关系式为.
19..解:(1)抛物线与直线交于轴上一点,
令 则
点
把,代入得:
,
解得:,
抛物线的解析式是;
(2)将直线与二次函数联立得方程组:
解得:或,
,
如图,要使的周长最小,则最小,
设二次函数与轴的另一交点为,
抛物线的对称轴为:
点,
连接 交对称轴于
,
此时,最小,
此时:,
的周长最小值为.
20.解:(1)对于:当x=0时,;
当y=0时,,妥得,x=3
∴A(3,0),B(0,)
把A(3,0),B(0,)代入得:
解得,
∴抛物线的解析式为:;
(2)抛物线的对称轴为直线
故设P(1,p),Q(m,n)
①当BC为菱形对角线时,如图,
∵B,C关于对称没对称,且对称轴与x轴垂直,
∴∴BC与对称轴垂直,且BC//x轴
∵在菱形BQCP中,BC⊥PQ
∴PQ⊥x轴
∵点P在x=1上,
∴点Q也在x=1上,
当x=1时,
∴Q(1,);
②当BC为菱形一边时,若点Q在点P右侧时,如图,
∴BC//PQ,且BC=PQ
∵BC//x轴,
∴令,则有
解得,
∴
∴PQ=BC=2
∵
∴PB=BC=2
∴迠P在x轴上,
∴P(1,0)
∴Q(3,0);
若点Q在点P的左侧,如图,
同理可得,Q(-1,0)
综上所述,Q点坐标为(1,)或(3,0)或(-1,0)
21.解:(1)由题意可得:,
解得:,
∴抛物线的解析式为:y=x2﹣3x﹣8;
(2)△ACD周长能取得最小值,
∵点A(﹣2,0),点B(8,0),
∴对称轴为直线x=3,
∵△ACD周长=AD+AC+CD,AC是定值,
∴当AD+CD取最小值时,△ACD周长能取得最小值,
∵点A,点B关于对称轴直线x=3对称,
∴连接BC交对称轴直线x=3于点D,此时AD+CD有最小值,
设直线BC解析式为:y=kx﹣8,
∴0=8k﹣8,
∴k=1,
∴直线BC解析式为:y=x﹣8,
当x=3,y=﹣5,
∴点D(3,﹣5);
(3)存在,
∵点A(﹣2,0),点C(0,﹣8),
∴直线AC解析式为y=﹣4x﹣8,
如图,
∵△ACE与△ACD面积相等,
∴DE∥AC,
∴设DE解析式为:y=﹣4x+n,
∴﹣5=﹣4×3+n,
∴n=7,
∴DE解析式为:y=﹣4x+7,
联立方程组可得:,
解得:,,
∴点E(﹣1,﹣4+11)或(﹣﹣1,4+11).
同课章节目录
