华东师大版九年级数学上册23.1成比例线段同步练习题(含解析)
文档属性
| 名称 | 华东师大版九年级数学上册23.1成比例线段同步练习题(含解析) |

|
|
| 格式 | docx | ||
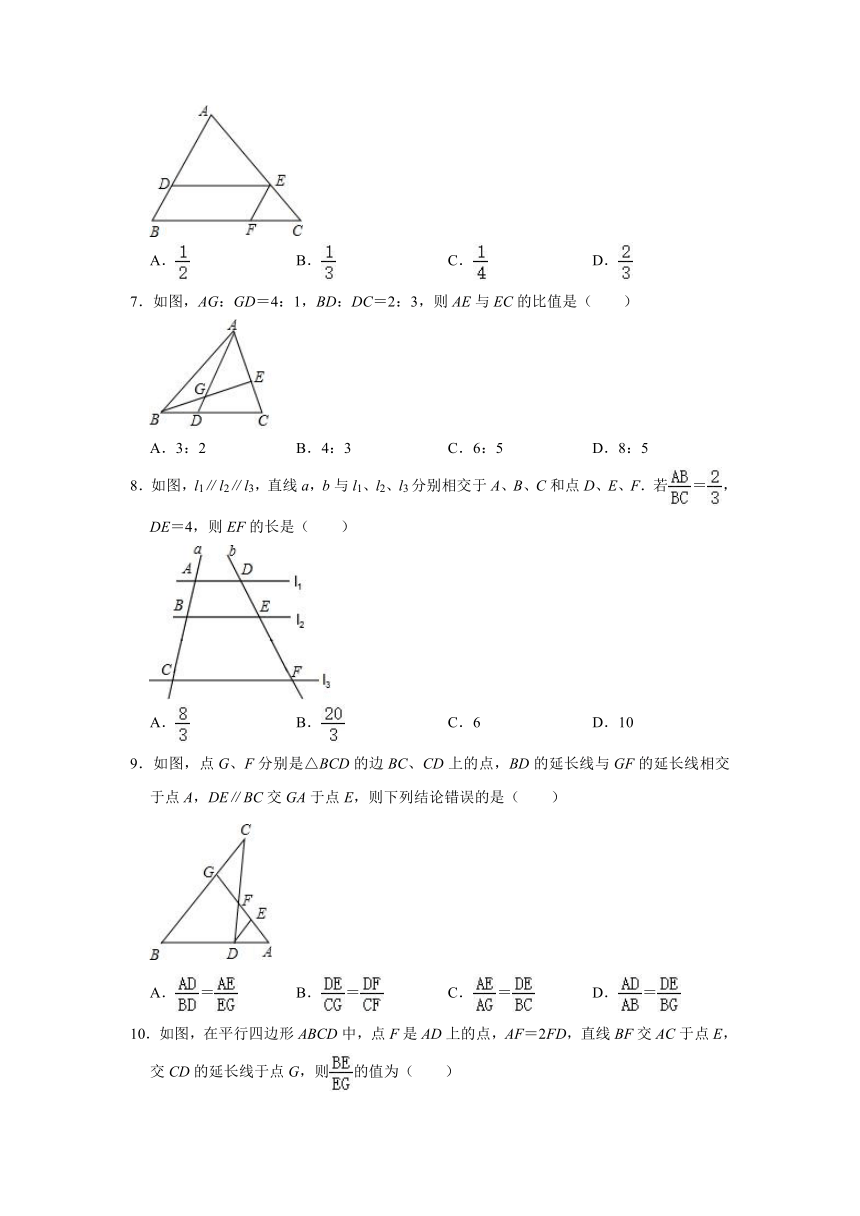
| 文件大小 | 234.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 00:00:00 | ||
图片预览



文档简介
2022-2023学年华东师大版九年级数学上册《23.1成比例线段》同步练习题(附答案)
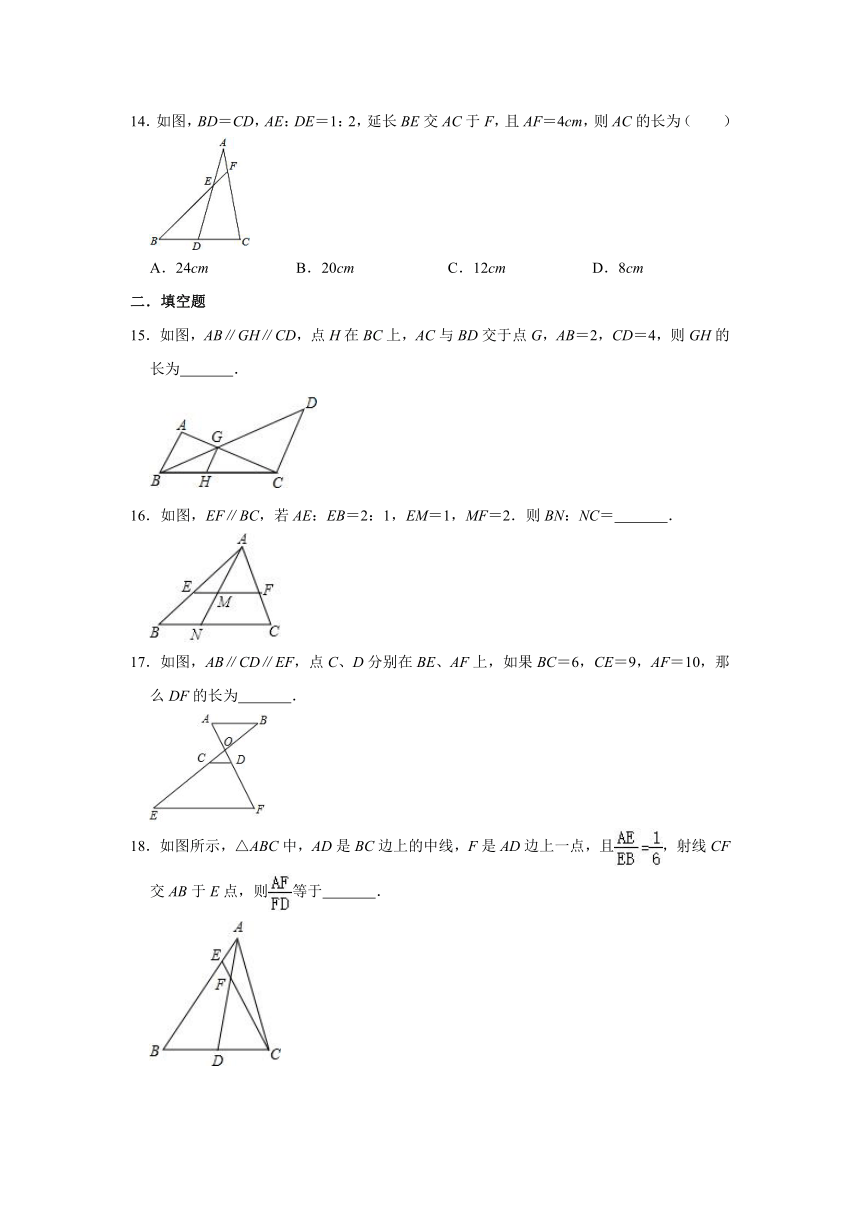
一.选择题
1.下列各组线段中,成比例的是( )
A.2cm,3cm,4cm,5cm B.2cm,4cm,6cm,8cm
C.3cm,6cm,8cm,12cm D.1cm,3cm,5cm,15cm
2.如果四条线段a、b、c、d构成=,m>0,则下列式子中,成立的是( )
A. B. C. D.
3.如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为( )
A.1 B.2 C.3 D.4
4.如图所示,△ABC中若DE∥BC,EF∥AB,则下列比例式正确的是( )
A. B. C. D.
5.如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F.已知,则的值为( )
A. B. C. D.
6.如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,EF∥AB.若AD=2BD,则的值为( )
A. B. C. D.
7.如图,AG:GD=4:1,BD:DC=2:3,则AE与EC的比值是( )
A.3:2 B.4:3 C.6:5 D.8:5
8.如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若=,DE=4,则EF的长是( )
A. B. C.6 D.10
9.如图,点G、F分别是△BCD的边BC、CD上的点,BD的延长线与GF的延长线相交于点A,DE∥BC交GA于点E,则下列结论错误的是( )
A.= B.= C.= D.=
10.如图,在平行四边形ABCD中,点F是AD上的点,AF=2FD,直线BF交AC于点E,交CD的延长线于点G,则的值为( )
A. B. C. D.
11.如图,已知DE∥BC,EF∥AB,现得到下列结论:
①;②;③;④.
其中正确比例式的个数有( )
A.4个 B.3个 C.2个 D.1个
12.如图,AB与CD相交于点E,点F在线段BC上,且AC∥EF∥DB.若BE=5,BF=3,AE=BC,则的值为( )
A. B. C. D.
13.如图,AB与CD相交于点E,AD∥BC,,CD=16,则DE的长为( )
A.3 B.6 C. D.10
14.如图,BD=CD,AE:DE=1:2,延长BE交AC于F,且AF=4cm,则AC的长为( )
A.24cm B.20cm C.12cm D.8cm
二.填空题
15.如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=4,则GH的长为 .
16.如图,EF∥BC,若AE:EB=2:1,EM=1,MF=2.则BN:NC= .
17.如图,AB∥CD∥EF,点C、D分别在BE、AF上,如果BC=6,CE=9,AF=10,那么DF的长为 .
18.如图所示,△ABC中,AD是BC边上的中线,F是AD边上一点,且,射线CF交AB于E点,则等于 .
19.如图,在△ABC中,AB=AC=12,AD⊥BC于点D,点E在AD上,且DE=2AE,连接BE并延长交AC于点F,则线段AF长为 .
20.如图,D是BC的中点,M是AD的中点,BM的延长线交AC于N,则AN:NC= .
三.解答题
21.已知a、b、c是△ABC的三边,且满足==,且a+b+c=12,请你探索△ABC的形状.
22.已知线段a、b、c满足a:b:c=3:2:6,且a+2b+c=26.
(1)求a、b、c的值;
(2)若线段x是线段a、b的比例中项,求x的值.
23.设a,b,c是△ABC的三条边,且,判断△ABC为何种三角形,并说明理由.
24.(1)已知a、b、c、d是成比例线段,其中a=3cm,b=2cm,c=6cm,求线段d的长.
(2)已知线段a、b、c,a=4cm,b=9cm,线段c是线段a和b的比例中项.求线段c的长.
25.(1)已知a=4,c=9,若b是a,c的比例中项,求b的值.
(2)已知线段MN是AB,CD的比例中项,AB=4cm,CD=5cm,求MN的长.并思考两题有何区别.
26.如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和D、E、F.若=,AC=14,
(1)求AB的长.
(2)如果AD=7,CF=14,求BE的长.
参考答案
一.选择题
1.解:A、∵2×5≠3×4,∴选项A不成比例;
B、∵2×8≠4×6,∴选项B不成比例;
C、∵3×12≠6×8,∴选项C不成比例;
D、∵1×15=3×5,∴选项D成比例.
故选:D.
2.解:A、∵=,m>0,∴=;故本选项错误;
B、∵=,m>0,∴≠;故本选项错误;
C、∵=,m>0,∴=﹣;故本选项错误;
D、∵=,m>0,∴=;故本选项正确.
故选:D.
3.解:∵DE∥BC,
∴,
即,
解得:EC=2,
故选:B.
4.解:∵DE∥BC,EF∥AB,
∴四边形DEFB是平行四边形,
∴DE=BF,BD=EF;
∵DE∥BC,
∴==,
==,
∵EF∥AB,
∴=,=,
∴,
故选:C.
5.解:∵l1∥l2∥l3,,
∴===,
故选:D.
6.解:∵DE∥BC,EF∥AB,AD=2BD,
∴==2,==2,
∴=,
故选:A.
7.解:过点D作DF∥CA交BE于F,如图,
∵DF∥CE,
∴=,
而BD:DC=2:3,
∴=,则CE=DF,
∵DF∥AE,
∴=,
∵AG:GD=4:1,
∴=,则AE=4DF,
∴==.
故选:D.
8.解:∵l1∥l2∥l3,
∴,
即,
解得:EF=6.
故选:C.
9.解:∵DE∥BC交GA于点E,
∴=,,,=,
∴A,B,D正确,C错误,
故选:C.
10.解:由AF=2DF,可以假设DF=k,则AF=2k,AD=3k,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AD=BC=3k,
∴==,
∴==
故选:C.
11.解:∵EF∥AB,
∴=,=,
即=,
∵DE∥BC,
∴==,
即=,
=≠,
所以①②④正确,故题中正确的个数为3个.
故选:B.
12.解:设CF=x,
∵EF∥AC,
∴=,
∴=,
解得x=,
∴CF=,
∵EF∥DB,
∴===.
故选:A.
13.解:∵AD∥BC,
∴BE:AE=CE:ED=3:5,
∵CD=16.CE+ED=CD,
∴DE=,
故选:D.
14.解:过D作DG∥BF交AC于G,则△AEF∽△ADG,
∵BD=CD,
∴CG=GF,AF:FG=AE:ED=1:2,
∵AF=4cm,
∴FG=2AF=8cm=CG,
∴AC=AF+FG+CG=20cm.
故选:B.
二.填空题
15.解:∵AB∥CH∥CD,
∴,,
∴+=+=1,
∵AB=2,CD=4,
∴+=1,
解得:GH=;
故答案为:.
16.解:∵AE:EB=2:1,
∴AE:AB=2:3,
∵EF∥BC,
∴===,
即==,
∴BN=1.5,NC=3,
∴BN:NC=1:2.
故答案为:1:2.
17.解:∵AB∥CD∥EF,
∴=,
∴=,
∴DF=6,
故答案为:6.
18.解:如图:过点D作DG∥EC交AB于G,
∵AD是BC边上的中线,
∴GD是△BEC的中位线,
∴BD=CD,BG=GE.
∵,
∴=
∵DG∥EC,
∴==.
故答案是:.
19.解:如图,作DH∥BF交AC于H.
∵AB=AC,AD⊥BC,
∴BD=CD,
∵DH∥BF,
∴CH=HF,
∵AE:DE=AF:FH=1:2,
∴AF=AC=,
故答案为.
20.解:作DE∥BN交AC于E,
∵DE∥BN,M是AD的中点,
∴N是AE的中点,
∵DE∥BN,D是BC的中点,
∴E是NC的中点,
∴AN:NC=1:2,
故答案为:1:2.
三.解答题
21.解:设===k,
可得a=3k﹣4,b=2k﹣3,c=4k﹣8,
代入a+b+c=12得:9k﹣15=12,
解得:k=3,
∴a=5,b=3,c=4,
则△ABC为直角三角形.
22.解:(1)∵a:b:c=3:2:6,
∴设a=3k,b=2k,c=6k,
又∵a+2b+c=26,
∴3k+2×2k+6k=26,解得k=2,
∴a=6,b=4,c=12;
(2)∵x是a、b的比例中项,
∴x2=ab,
∴x2=4×6,
∴x=2或x=﹣2(舍去),
即x的值为.
23.解:△ABC为等边三角形,理由如下:
∵a,b,c是△ABC的三条边,
∴a+b+c≠0,
∵,
∴==0,
∴a﹣b=0,b﹣c=0,c﹣a=0,
∴a=b=c,
∴△ABC为等边三角形.
24.解:(1)∵a、b、c、d是成比例线段,
∴a:b=c:d,
∵a=3cm,b=2cm,c=6cm,
∴d=4cm;
(2)∵线段c是线段a和b的比例中项,a=4cm,b=9cm,
∴c2=ab=36,
解得:c=±6,
又∵线段是正数,
∴c=6cm.
25.解:(1)∵b是a,c的比例中项,
∴a:b=b:c,
∴b2=ac;
b=±,
∵a=4,c=9,
∴b=±=±6,即b=±6;
(2)∵MN是线段,
∴MN>0;
∵线段MN是AB,CD的比例中项,
∴AB:MN=MN:CD,
∴MN2=AB CD,
∴MN=±;
∵AB=4cm,CD=5cm,
∴MN=±cm=±2cm;
MN不可能为负值,则MN=2cm,
通过解答(1)、(2)发现,c、MN同时作为比例中项出现,c可以取负值,而MN不可以取负值.
26.解:(1)∵AD∥BE∥CF,
∴,
∴,
∵AC=14,
∴AB=4,
(2)过点A作AG∥DF交BE于点H,交CF于点G,如图所示:
又∵AD∥BE∥CF,AD=7,
∴AD=HE=GF=7,
∵CF=14,
∴CG=14﹣7=7,
∵BE∥CF,
∴,
∴BH=2,
∴BE=2+7=9.
一.选择题
1.下列各组线段中,成比例的是( )
A.2cm,3cm,4cm,5cm B.2cm,4cm,6cm,8cm
C.3cm,6cm,8cm,12cm D.1cm,3cm,5cm,15cm
2.如果四条线段a、b、c、d构成=,m>0,则下列式子中,成立的是( )
A. B. C. D.
3.如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为( )
A.1 B.2 C.3 D.4
4.如图所示,△ABC中若DE∥BC,EF∥AB,则下列比例式正确的是( )
A. B. C. D.
5.如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F.已知,则的值为( )
A. B. C. D.
6.如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,EF∥AB.若AD=2BD,则的值为( )
A. B. C. D.
7.如图,AG:GD=4:1,BD:DC=2:3,则AE与EC的比值是( )
A.3:2 B.4:3 C.6:5 D.8:5
8.如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若=,DE=4,则EF的长是( )
A. B. C.6 D.10
9.如图,点G、F分别是△BCD的边BC、CD上的点,BD的延长线与GF的延长线相交于点A,DE∥BC交GA于点E,则下列结论错误的是( )
A.= B.= C.= D.=
10.如图,在平行四边形ABCD中,点F是AD上的点,AF=2FD,直线BF交AC于点E,交CD的延长线于点G,则的值为( )
A. B. C. D.
11.如图,已知DE∥BC,EF∥AB,现得到下列结论:
①;②;③;④.
其中正确比例式的个数有( )
A.4个 B.3个 C.2个 D.1个
12.如图,AB与CD相交于点E,点F在线段BC上,且AC∥EF∥DB.若BE=5,BF=3,AE=BC,则的值为( )
A. B. C. D.
13.如图,AB与CD相交于点E,AD∥BC,,CD=16,则DE的长为( )
A.3 B.6 C. D.10
14.如图,BD=CD,AE:DE=1:2,延长BE交AC于F,且AF=4cm,则AC的长为( )
A.24cm B.20cm C.12cm D.8cm
二.填空题
15.如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=4,则GH的长为 .
16.如图,EF∥BC,若AE:EB=2:1,EM=1,MF=2.则BN:NC= .
17.如图,AB∥CD∥EF,点C、D分别在BE、AF上,如果BC=6,CE=9,AF=10,那么DF的长为 .
18.如图所示,△ABC中,AD是BC边上的中线,F是AD边上一点,且,射线CF交AB于E点,则等于 .
19.如图,在△ABC中,AB=AC=12,AD⊥BC于点D,点E在AD上,且DE=2AE,连接BE并延长交AC于点F,则线段AF长为 .
20.如图,D是BC的中点,M是AD的中点,BM的延长线交AC于N,则AN:NC= .
三.解答题
21.已知a、b、c是△ABC的三边,且满足==,且a+b+c=12,请你探索△ABC的形状.
22.已知线段a、b、c满足a:b:c=3:2:6,且a+2b+c=26.
(1)求a、b、c的值;
(2)若线段x是线段a、b的比例中项,求x的值.
23.设a,b,c是△ABC的三条边,且,判断△ABC为何种三角形,并说明理由.
24.(1)已知a、b、c、d是成比例线段,其中a=3cm,b=2cm,c=6cm,求线段d的长.
(2)已知线段a、b、c,a=4cm,b=9cm,线段c是线段a和b的比例中项.求线段c的长.
25.(1)已知a=4,c=9,若b是a,c的比例中项,求b的值.
(2)已知线段MN是AB,CD的比例中项,AB=4cm,CD=5cm,求MN的长.并思考两题有何区别.
26.如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和D、E、F.若=,AC=14,
(1)求AB的长.
(2)如果AD=7,CF=14,求BE的长.
参考答案
一.选择题
1.解:A、∵2×5≠3×4,∴选项A不成比例;
B、∵2×8≠4×6,∴选项B不成比例;
C、∵3×12≠6×8,∴选项C不成比例;
D、∵1×15=3×5,∴选项D成比例.
故选:D.
2.解:A、∵=,m>0,∴=;故本选项错误;
B、∵=,m>0,∴≠;故本选项错误;
C、∵=,m>0,∴=﹣;故本选项错误;
D、∵=,m>0,∴=;故本选项正确.
故选:D.
3.解:∵DE∥BC,
∴,
即,
解得:EC=2,
故选:B.
4.解:∵DE∥BC,EF∥AB,
∴四边形DEFB是平行四边形,
∴DE=BF,BD=EF;
∵DE∥BC,
∴==,
==,
∵EF∥AB,
∴=,=,
∴,
故选:C.
5.解:∵l1∥l2∥l3,,
∴===,
故选:D.
6.解:∵DE∥BC,EF∥AB,AD=2BD,
∴==2,==2,
∴=,
故选:A.
7.解:过点D作DF∥CA交BE于F,如图,
∵DF∥CE,
∴=,
而BD:DC=2:3,
∴=,则CE=DF,
∵DF∥AE,
∴=,
∵AG:GD=4:1,
∴=,则AE=4DF,
∴==.
故选:D.
8.解:∵l1∥l2∥l3,
∴,
即,
解得:EF=6.
故选:C.
9.解:∵DE∥BC交GA于点E,
∴=,,,=,
∴A,B,D正确,C错误,
故选:C.
10.解:由AF=2DF,可以假设DF=k,则AF=2k,AD=3k,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AD=BC=3k,
∴==,
∴==
故选:C.
11.解:∵EF∥AB,
∴=,=,
即=,
∵DE∥BC,
∴==,
即=,
=≠,
所以①②④正确,故题中正确的个数为3个.
故选:B.
12.解:设CF=x,
∵EF∥AC,
∴=,
∴=,
解得x=,
∴CF=,
∵EF∥DB,
∴===.
故选:A.
13.解:∵AD∥BC,
∴BE:AE=CE:ED=3:5,
∵CD=16.CE+ED=CD,
∴DE=,
故选:D.
14.解:过D作DG∥BF交AC于G,则△AEF∽△ADG,
∵BD=CD,
∴CG=GF,AF:FG=AE:ED=1:2,
∵AF=4cm,
∴FG=2AF=8cm=CG,
∴AC=AF+FG+CG=20cm.
故选:B.
二.填空题
15.解:∵AB∥CH∥CD,
∴,,
∴+=+=1,
∵AB=2,CD=4,
∴+=1,
解得:GH=;
故答案为:.
16.解:∵AE:EB=2:1,
∴AE:AB=2:3,
∵EF∥BC,
∴===,
即==,
∴BN=1.5,NC=3,
∴BN:NC=1:2.
故答案为:1:2.
17.解:∵AB∥CD∥EF,
∴=,
∴=,
∴DF=6,
故答案为:6.
18.解:如图:过点D作DG∥EC交AB于G,
∵AD是BC边上的中线,
∴GD是△BEC的中位线,
∴BD=CD,BG=GE.
∵,
∴=
∵DG∥EC,
∴==.
故答案是:.
19.解:如图,作DH∥BF交AC于H.
∵AB=AC,AD⊥BC,
∴BD=CD,
∵DH∥BF,
∴CH=HF,
∵AE:DE=AF:FH=1:2,
∴AF=AC=,
故答案为.
20.解:作DE∥BN交AC于E,
∵DE∥BN,M是AD的中点,
∴N是AE的中点,
∵DE∥BN,D是BC的中点,
∴E是NC的中点,
∴AN:NC=1:2,
故答案为:1:2.
三.解答题
21.解:设===k,
可得a=3k﹣4,b=2k﹣3,c=4k﹣8,
代入a+b+c=12得:9k﹣15=12,
解得:k=3,
∴a=5,b=3,c=4,
则△ABC为直角三角形.
22.解:(1)∵a:b:c=3:2:6,
∴设a=3k,b=2k,c=6k,
又∵a+2b+c=26,
∴3k+2×2k+6k=26,解得k=2,
∴a=6,b=4,c=12;
(2)∵x是a、b的比例中项,
∴x2=ab,
∴x2=4×6,
∴x=2或x=﹣2(舍去),
即x的值为.
23.解:△ABC为等边三角形,理由如下:
∵a,b,c是△ABC的三条边,
∴a+b+c≠0,
∵,
∴==0,
∴a﹣b=0,b﹣c=0,c﹣a=0,
∴a=b=c,
∴△ABC为等边三角形.
24.解:(1)∵a、b、c、d是成比例线段,
∴a:b=c:d,
∵a=3cm,b=2cm,c=6cm,
∴d=4cm;
(2)∵线段c是线段a和b的比例中项,a=4cm,b=9cm,
∴c2=ab=36,
解得:c=±6,
又∵线段是正数,
∴c=6cm.
25.解:(1)∵b是a,c的比例中项,
∴a:b=b:c,
∴b2=ac;
b=±,
∵a=4,c=9,
∴b=±=±6,即b=±6;
(2)∵MN是线段,
∴MN>0;
∵线段MN是AB,CD的比例中项,
∴AB:MN=MN:CD,
∴MN2=AB CD,
∴MN=±;
∵AB=4cm,CD=5cm,
∴MN=±cm=±2cm;
MN不可能为负值,则MN=2cm,
通过解答(1)、(2)发现,c、MN同时作为比例中项出现,c可以取负值,而MN不可以取负值.
26.解:(1)∵AD∥BE∥CF,
∴,
∴,
∵AC=14,
∴AB=4,
(2)过点A作AG∥DF交BE于点H,交CF于点G,如图所示:
又∵AD∥BE∥CF,AD=7,
∴AD=HE=GF=7,
∵CF=14,
∴CG=14﹣7=7,
∵BE∥CF,
∴,
∴BH=2,
∴BE=2+7=9.
