人教版数学七年级上册1.5.3近似数 教案 (表格式)
文档属性
| 名称 | 人教版数学七年级上册1.5.3近似数 教案 (表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 673.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 00:00:00 | ||
图片预览


文档简介
1.5.3近似数教案
教学目标
1. 了解准确数与近似数的概念,并会用精确度来表示准确数与近似数的接近程度;
2. 掌握用四舍五入法求一个数的近似数;
3. 经历从现实情境中抽象出准确数与近似数概念的过程,培养学生的数学抽象能力;
4. 通过将实际问题转化为数学问题这一过程,增强学生对数学学习的兴趣,进一步证实了数学在实际应用过程中的广泛性.
二、教学重难点
重点:掌握用四舍五入法求一个数的近似数的方法
难点:掌握用四舍五入法求一个数的近似数的方法
三、教学用具
多媒体等.
四、教学过程设计
教学 环节 教师活动 学生活动 设计意图
【学习目标】 1. 了解准确数与近似数的概念,并会用精确度来表示准确数与近似数的接近程度; 2. 掌握用四舍五入法求一个数的近似数; 3. 经历从现实情境中抽象出准确数与近似数概念的过程,培养学生的数学抽象能力; 4. 通过将实际问题转化为数学问题这一过程,增强学生对数学学习的兴趣,进一步证实了数学在实际应用过程中的广泛性. 熟悉学习目标 通过学习目标让学生熟悉本节课要讲解的内容.
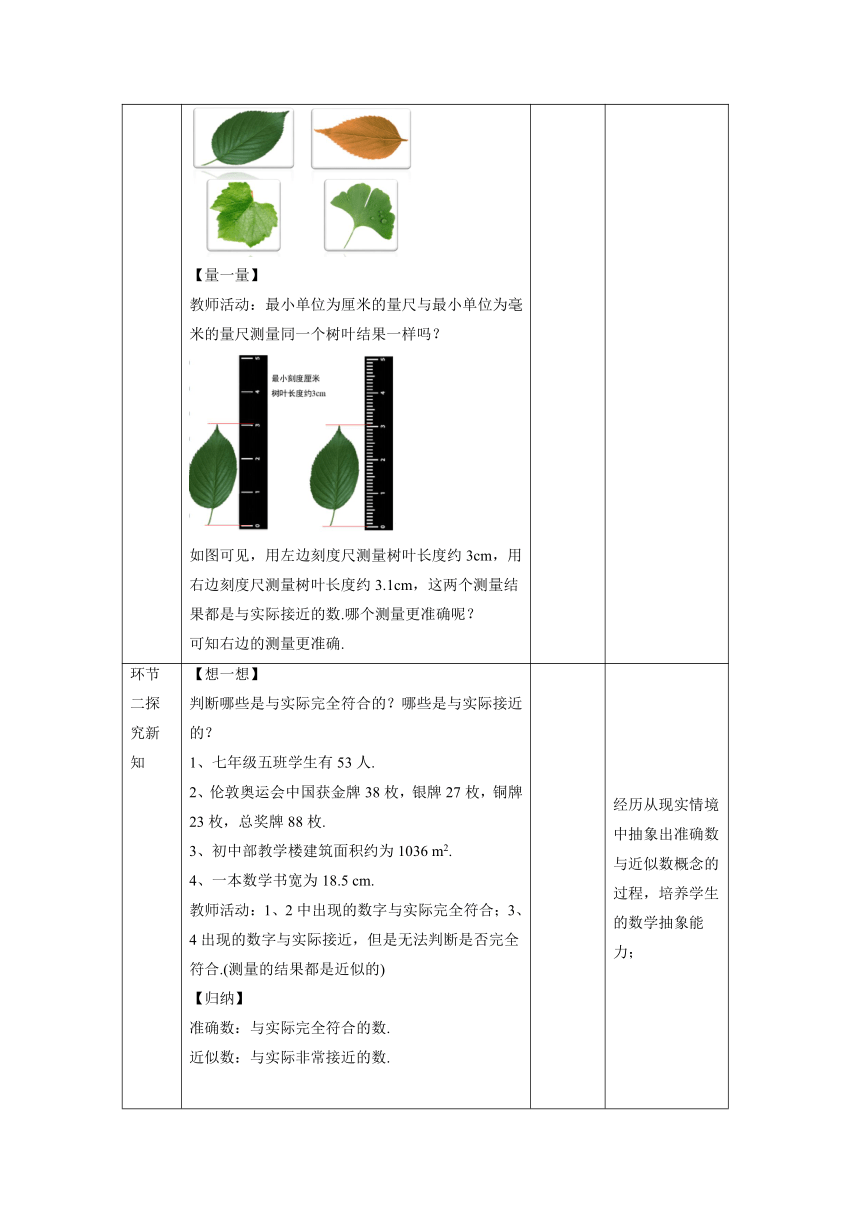
环节一 创设情景 【量一量】 教师活动:课后作业让大家准备了一个树叶 测量自己的树叶长度,测量同桌的树叶长度,两个人测量结果一样吗? 展示学生测量结果,展现出测量结果有误差. 【量一量】 教师活动:最小单位为厘米的量尺与最小单位为毫米的量尺测量同一个树叶结果一样吗? 如图可见,用左边刻度尺测量树叶长度约3cm,用右边刻度尺测量树叶长度约3.1cm,这两个测量结果都是与实际接近的数.哪个测量更准确呢? 可知右边的测量更准确. 拿出树叶,测量长度.
环节二探究新知 【想一想】 判断哪些是与实际完全符合的?哪些是与实际接近的? 1、七年级五班学生有53人. 2、伦敦奥运会中国获金牌38枚,银牌27枚,铜牌23枚,总奖牌88枚. 3、初中部教学楼建筑面积约为1036 m2. 4、一本数学书宽为18.5 cm. 教师活动:1、2中出现的数字与实际完全符合;3、4出现的数字与实际接近,但是无法判断是否完全符合.(测量的结果都是近似的) 【归纳】 准确数:与实际完全符合的数. 近似数:与实际非常接近的数. 注意: 语句中带有“约”“左右”等词语,描述的数据是近似数; 描述“温度”“身高”“体重”等测量、称重的数据都是近似数. 【想一想】 判断哪些是与实际完全符合的?哪些是与实际接近的? 教师活动:1、2中出现的数字是准确数;3、4出现的数字是近似数. 【交流】 下列各数,哪些是近似数,哪些是准确数? (1) 1小时30分. (2) 绿化队今年植树约2万棵. (3) 小明到书店买了10本书. (4) 一次数学测验中,有2人得100分. (5) 某区在校中学生近5万人. (6) 七年级二班有44人. (7) 王红的身高165厘米. (8) 李强的体重55公斤. 答:近似数(2)(5)(7)(8) 准确数:(1)(3)(4)(6) 【思考】 既然有了准确数,为何还需要近似数呢? 有时是因为客观条件的约束,很难得到准确数 如:测算宇宙的年龄,圆周率π 有时是因为不需要得到准确数 如:测量某人的身高 【思考】 对于参加同一个会议的人数,有两个报道. 一个报道说:“会议秘书处宣布,参加今天会议的有513人.”另一个报道说:“约有500人参加了今天的会议.” 教师活动:513是准确数,500是近似数.可见,此近似数与准确数的误差是13. 【思考】 怎么描述近似数与准确数的精确程度呢? 答案:精确度 提醒:四舍五入到哪一位,就说这个近似数精确到哪一位. 【想一想】 按四舍五入法对圆周率π取近似值时,有 π≈3(精确到个位), π≈3.1(精确到0.1,或叫做精确到十分位), π≈3.14(精确到0.01,或叫做精确到百分位), π≈3.142(精确到__0.001_,或叫做精确到_千分位_), π≈3.1416(精确到_0.0001_ ,或叫做精确到_万分位___). 经历从现实情境中抽象出准确数与近似数概念的过程,培养学生的数学抽象能力; 通过将实际问题转化为数学问题这一过程,增强学生对数学学习的兴趣,进一步证实了数学在实际应用过程中的广泛性.
环节三应用新知 【典型例题】 例 按括号内的要求,用四舍五入法对下列各数取近似数: (1)0.0158(精确到0.001); (2) 304.35≈304 (精确到个位); (3)1.804(精确到0.1); (4)1.804 ≈1.80 (精确到0.01). 解: (1)0.0158≈0.016;(2) 304.35≈304;(3)1.804 ≈1.8; (4)1.804 ≈1.80. 注意:近似数末尾的0不能省略,1.80与1.8不同 例 下列由四舍五入法得到的近似数,各精确到哪一位? (1)2.4万精确到__千位____ (2) 2.4×104精确到__千位____ (3)150万精确到__万位____ (4)1.50×106精确到__万位____ 注意:带有百、千、万、亿等单位及科学记数法表示的数,应先将该数还原成原数,看末位数处在原数的什么位置上,就是精确到什么位置上.
环节四 巩固新知 【随堂练习】 练习1 用四舍五入法,取1.2945精确到百分位的近似值得( ). A.1.29 B.1.290 C.1.3 D.1.30 答案:A 练习2 用四舍五入法,不能得到近似值761的数是( ). A.760.91 B.760.5 C.761.34 D.761.52 答案: D 练习3 2016年河南省生产总值约40160.01亿元,40160.01亿精确到( )位. A.十分位 B.百分位 C.百万位 D.亿位 答案:C 练习4 近似数1.30所表示的准确数A的范围是 ( ). A.1.25≤A<1.35 B.1.20 <A<1.30 C.1.295≤A<1.305 D.1.300≤A<1.305 答案:C 练习5 下列用科学记数法表示的近似数,各精确到哪一位? (1) 4.8×105 (2) 1.0×107 (3) 6.414×103 (4) 9.7×106 解: (1) 4.8×105精确到万位. (2) 1.0×107精确到百万位. (3) 6.414×103精确到个位. (4) 9.7×106精确到十万位. 做练习 巩固用四舍五入法求一个数的近似数及掌握近似数的精确度.
环节五 课堂小结 以思维导图的形式呈现本节课所讲解的内容. 回顾本节课所讲的内容 通过小结让学生进一步熟悉巩固本节课所学的知识.
环节六 布置作业 教科书 第46页练习题. 第47页习题1.5中6. 课后完成练习 通过课后作业,教师能及时了解学生对本节课知识的掌握情况,以便对教学进度和方法进行适当的调整.
教学目标
1. 了解准确数与近似数的概念,并会用精确度来表示准确数与近似数的接近程度;
2. 掌握用四舍五入法求一个数的近似数;
3. 经历从现实情境中抽象出准确数与近似数概念的过程,培养学生的数学抽象能力;
4. 通过将实际问题转化为数学问题这一过程,增强学生对数学学习的兴趣,进一步证实了数学在实际应用过程中的广泛性.
二、教学重难点
重点:掌握用四舍五入法求一个数的近似数的方法
难点:掌握用四舍五入法求一个数的近似数的方法
三、教学用具
多媒体等.
四、教学过程设计
教学 环节 教师活动 学生活动 设计意图
【学习目标】 1. 了解准确数与近似数的概念,并会用精确度来表示准确数与近似数的接近程度; 2. 掌握用四舍五入法求一个数的近似数; 3. 经历从现实情境中抽象出准确数与近似数概念的过程,培养学生的数学抽象能力; 4. 通过将实际问题转化为数学问题这一过程,增强学生对数学学习的兴趣,进一步证实了数学在实际应用过程中的广泛性. 熟悉学习目标 通过学习目标让学生熟悉本节课要讲解的内容.
环节一 创设情景 【量一量】 教师活动:课后作业让大家准备了一个树叶 测量自己的树叶长度,测量同桌的树叶长度,两个人测量结果一样吗? 展示学生测量结果,展现出测量结果有误差. 【量一量】 教师活动:最小单位为厘米的量尺与最小单位为毫米的量尺测量同一个树叶结果一样吗? 如图可见,用左边刻度尺测量树叶长度约3cm,用右边刻度尺测量树叶长度约3.1cm,这两个测量结果都是与实际接近的数.哪个测量更准确呢? 可知右边的测量更准确. 拿出树叶,测量长度.
环节二探究新知 【想一想】 判断哪些是与实际完全符合的?哪些是与实际接近的? 1、七年级五班学生有53人. 2、伦敦奥运会中国获金牌38枚,银牌27枚,铜牌23枚,总奖牌88枚. 3、初中部教学楼建筑面积约为1036 m2. 4、一本数学书宽为18.5 cm. 教师活动:1、2中出现的数字与实际完全符合;3、4出现的数字与实际接近,但是无法判断是否完全符合.(测量的结果都是近似的) 【归纳】 准确数:与实际完全符合的数. 近似数:与实际非常接近的数. 注意: 语句中带有“约”“左右”等词语,描述的数据是近似数; 描述“温度”“身高”“体重”等测量、称重的数据都是近似数. 【想一想】 判断哪些是与实际完全符合的?哪些是与实际接近的? 教师活动:1、2中出现的数字是准确数;3、4出现的数字是近似数. 【交流】 下列各数,哪些是近似数,哪些是准确数? (1) 1小时30分. (2) 绿化队今年植树约2万棵. (3) 小明到书店买了10本书. (4) 一次数学测验中,有2人得100分. (5) 某区在校中学生近5万人. (6) 七年级二班有44人. (7) 王红的身高165厘米. (8) 李强的体重55公斤. 答:近似数(2)(5)(7)(8) 准确数:(1)(3)(4)(6) 【思考】 既然有了准确数,为何还需要近似数呢? 有时是因为客观条件的约束,很难得到准确数 如:测算宇宙的年龄,圆周率π 有时是因为不需要得到准确数 如:测量某人的身高 【思考】 对于参加同一个会议的人数,有两个报道. 一个报道说:“会议秘书处宣布,参加今天会议的有513人.”另一个报道说:“约有500人参加了今天的会议.” 教师活动:513是准确数,500是近似数.可见,此近似数与准确数的误差是13. 【思考】 怎么描述近似数与准确数的精确程度呢? 答案:精确度 提醒:四舍五入到哪一位,就说这个近似数精确到哪一位. 【想一想】 按四舍五入法对圆周率π取近似值时,有 π≈3(精确到个位), π≈3.1(精确到0.1,或叫做精确到十分位), π≈3.14(精确到0.01,或叫做精确到百分位), π≈3.142(精确到__0.001_,或叫做精确到_千分位_), π≈3.1416(精确到_0.0001_ ,或叫做精确到_万分位___). 经历从现实情境中抽象出准确数与近似数概念的过程,培养学生的数学抽象能力; 通过将实际问题转化为数学问题这一过程,增强学生对数学学习的兴趣,进一步证实了数学在实际应用过程中的广泛性.
环节三应用新知 【典型例题】 例 按括号内的要求,用四舍五入法对下列各数取近似数: (1)0.0158(精确到0.001); (2) 304.35≈304 (精确到个位); (3)1.804(精确到0.1); (4)1.804 ≈1.80 (精确到0.01). 解: (1)0.0158≈0.016;(2) 304.35≈304;(3)1.804 ≈1.8; (4)1.804 ≈1.80. 注意:近似数末尾的0不能省略,1.80与1.8不同 例 下列由四舍五入法得到的近似数,各精确到哪一位? (1)2.4万精确到__千位____ (2) 2.4×104精确到__千位____ (3)150万精确到__万位____ (4)1.50×106精确到__万位____ 注意:带有百、千、万、亿等单位及科学记数法表示的数,应先将该数还原成原数,看末位数处在原数的什么位置上,就是精确到什么位置上.
环节四 巩固新知 【随堂练习】 练习1 用四舍五入法,取1.2945精确到百分位的近似值得( ). A.1.29 B.1.290 C.1.3 D.1.30 答案:A 练习2 用四舍五入法,不能得到近似值761的数是( ). A.760.91 B.760.5 C.761.34 D.761.52 答案: D 练习3 2016年河南省生产总值约40160.01亿元,40160.01亿精确到( )位. A.十分位 B.百分位 C.百万位 D.亿位 答案:C 练习4 近似数1.30所表示的准确数A的范围是 ( ). A.1.25≤A<1.35 B.1.20 <A<1.30 C.1.295≤A<1.305 D.1.300≤A<1.305 答案:C 练习5 下列用科学记数法表示的近似数,各精确到哪一位? (1) 4.8×105 (2) 1.0×107 (3) 6.414×103 (4) 9.7×106 解: (1) 4.8×105精确到万位. (2) 1.0×107精确到百万位. (3) 6.414×103精确到个位. (4) 9.7×106精确到十万位. 做练习 巩固用四舍五入法求一个数的近似数及掌握近似数的精确度.
环节五 课堂小结 以思维导图的形式呈现本节课所讲解的内容. 回顾本节课所讲的内容 通过小结让学生进一步熟悉巩固本节课所学的知识.
环节六 布置作业 教科书 第46页练习题. 第47页习题1.5中6. 课后完成练习 通过课后作业,教师能及时了解学生对本节课知识的掌握情况,以便对教学进度和方法进行适当的调整.
