鲁教版(五四学制)九年级数学上册第3章二次函数商品销售利润问题解答题专题训练(含解析)
文档属性
| 名称 | 鲁教版(五四学制)九年级数学上册第3章二次函数商品销售利润问题解答题专题训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 147.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 00:00:00 | ||
图片预览




文档简介
2022-2023学年鲁教版(五四学制)九年级数学上册《第3章二次函数》
商品销售利润问题解答题专题训练(附答案)
1.某超市购进一批时令水果,成本为10元/千克,根据市场调研发现,这种水果在未来30天的销售单价m(元/千克)与时间x(天)之间的函数关系式为m=x+20(1≤x≤30,x为整数),且其日销售量y(千克)与时间x(天)之间的函数关系如图所示:
(1)求每天销售这种水果的利润W(元)与x(天)之间的函数关系式;
(2)求x为何值时,日销售利润为900元;
(3)直接写出哪一天销售这种水果的利润最大?最大日销售利润为多少元?
2.已知某商品的进价为每件24元,现在售价为每件32元,每天可售出200件.经市场调查发现:若该商品每件涨价1元,则每天就会少卖5件.
那么每件涨价多少元时每天获得利润最大?所获最大利润是多少元?
3.某商品的进价是每件40元,当售价每件60元时,当天可售出300件.进行不同程度的涨价后,发现每涨价1元,当天销售量减少10件.设商品售价每件涨价x元(x为正整数)时,当天售出商品的利润为y元.
(1)求y与x之间的函数关系式;
(2)如何定价,才能使商品当天的销售利润达到6250元?
4.李大爷每年春节期间都会购进一批新年红包销售,根据往年的销售经验,这种红包平均每天可销售50袋,每袋盈利3元,若每袋降价0.5元,平均每天可多售出25袋,设每袋降x元,平均每天的利润为y元.
(1)请求出y与x的函数表达式;
(2)若李大爷想让每天的利润最大化,应该降价多少元销售?最大利润为多少元?
5.已知某品牌床单进价为每件60元,每月的销量y(件)与售价x(元)的相关信息如表(符合一次函数关系):
售价(元/件) 100 110 120 130 …
月销售量(件) 200 180 160 140 …
(Ⅰ)销售该品牌床单每件的利润是 元(用含x的式子表示);
(Ⅱ)用含x的代数式表示月销量y;
(Ⅲ)设销售该品牌床单的月利润为w元,那么售价为多少时,当月的利润最大,最大利润是多少?
6.某种蔬菜在3﹣6月份的销售单价与销售月份之间的关系如图(甲)所示,成本与销售月份之间的关系如图(乙)所示.(图(甲)中4个点在一条直线上,图(乙)中的4个点在一条抛物线上)
(1)求该蔬菜5月份的销售单价.(精确到0.1元)
(2)求该蔬菜4月份每千克的成本.(精确到0.1元)
(3)哪个月出售这种蔬菜,每千克的收益最大?每千克的最大收益是多少元?(收益=售价﹣成本)
7.某商店销售一种商品,经市场调查发现:该商品的周销售量y(件)是售价x(元/件)的一次函数,其售价、周销售量、周销售利润w(元)的两组对应值如表:
售价x(元/件) 40 50
周销售量y(件) 120 100
周销售利润w(元) 2400 3000
注:周销售利润=周销售量×(售价﹣进价)
(1)每件商品的进价为 元/件,y与x的函数关系式为 (不要求写出自变量的取值范围);
(2)当每件商品售价x为多少元时,周销售利润w最大?并求出此时的最大利润;
(3)若该商品每件进价提高了4元,其每件售价不超过m元(m是大于50的常数,且是整数),该商店在销售中,周销售量与售价仍满足(1)中的函数关系,直接写出周销售的最大利润.
8.疫情期间,某核酸检测点要检测1000人,排队前来检测的人数y与时间x(小时)之间符合函数表达式:y=200x(x≤5)该检测点实际检测的人数m与时间t(小时)统计如下表所示:
t 0 1 2 3 4 …
m 0 40 160 360 640 …
(1)猜想该检测点检测的人数m关于t的函数表达式,并说明理由;
(2)几小时后所有人可以完成检测?
(3)因准备需要,排队2小时才开始检测,排队等候检测人数最多时有多少人?
9.鱼卷是泉州十大名小吃之一,不但本地人喜欢,还深受外来游客的赞赏.小张从事鱼卷生产和批发多年,有着不少来自零售商和酒店的客户,当地的习俗是农历正月没有生产鱼卷,客户正月所需要的鱼卷都会在农历十二月底进行一次性采购.2018年年底小张的“熟客”们共向小张采购了5000箱鱼卷,到2020年底“熟客”们采购了7200箱.
(1)求小张的“熟客“们这两年向小张采购鱼卷的年平均增长率;
(2)2020年底小张“熟客”们采订购鱼卷的数量占小张年底总销售量的,由于鱼卷受到游客们的青睐,小张做了一份市场调查,决定今年年底是否在网上出售鱼卷,若没有在网上出售鱼卷,则按去年的价格出售,每箱利润为15元,预计销售量与去年持平;若计划在网上出售鱼卷,则需把每箱售价下调1至5元,且每下调1元销售量可增加1000箱,求小张在今年年底能获得的最大利润是多少元?
10.农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格x(元/千克) 30 35 40 45 60
日销售量p(千克) 600 450 300 150 0
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式;
(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
11.某校数学综合实践小组去超市调查某种商品“十一”期间的销售情况,下面是调查后小明与其他两位同学交流的情况:
小明:据调查,该商品的进价为12元/件.
小亮:该商品定价为20元时,每天可售240件;
小颖:在定价为20元的基础上,每涨价1元,每天少售10件.
根据他们的对话,解决下列问题:
(1)若销售该商品每天能获利2470元,则该商品的定价应为多少元?
(2)设该商品的销售单价为m元时,每天销售该商品可获利W元,若每件商品销售单价不高于26元,则销售单价定为多少元时每天获利最大?最大利润是多少元?
12.如图,正方形ABCD的边长为6cm,P,Q两动点同时从点C出发,点P沿CB→BA以3cm/s的速度向终点A匀速运动,点Q沿CD→DB以2cm/s的速度向点B匀速运动,当点P到达终点A时,点Q同时停止运动.设点P的运动时间为t(s),△CPQ的面积为S(cm2).
(1)填空:点P的运动时间为 s;
(2)求S关于t的函数解析式,并直接写出自变量t的取值范围.
13.云南有着复杂的自然地理条件,十分有利于中药材的生长.某种中药材成本每斤500元某药材公司试销一段时间发现:每周的销售量y(斤)与销售单价x(元/斤)满足的关系如下表:
x(元/斤) 550 600 650 680
y(斤) 450 400 350 320
(1)请根据表中的数据写出y与x之间的函数关系式;
(2)根据有关部门规定,该药材售价不允许超过700元.该药材公司每周获利w元,试写w与x之间的函数关系式,并求出药材公司每周的最大利润.
(3)在(2)的条件下,若该药材公司每周获利不少于40000元,试确定销售单价x的取值范围.
14.某种商品每件的进价为30元,在某段时间内若以每件x元出售,可卖出(100﹣x)件,应如何定价才能使利润最大?
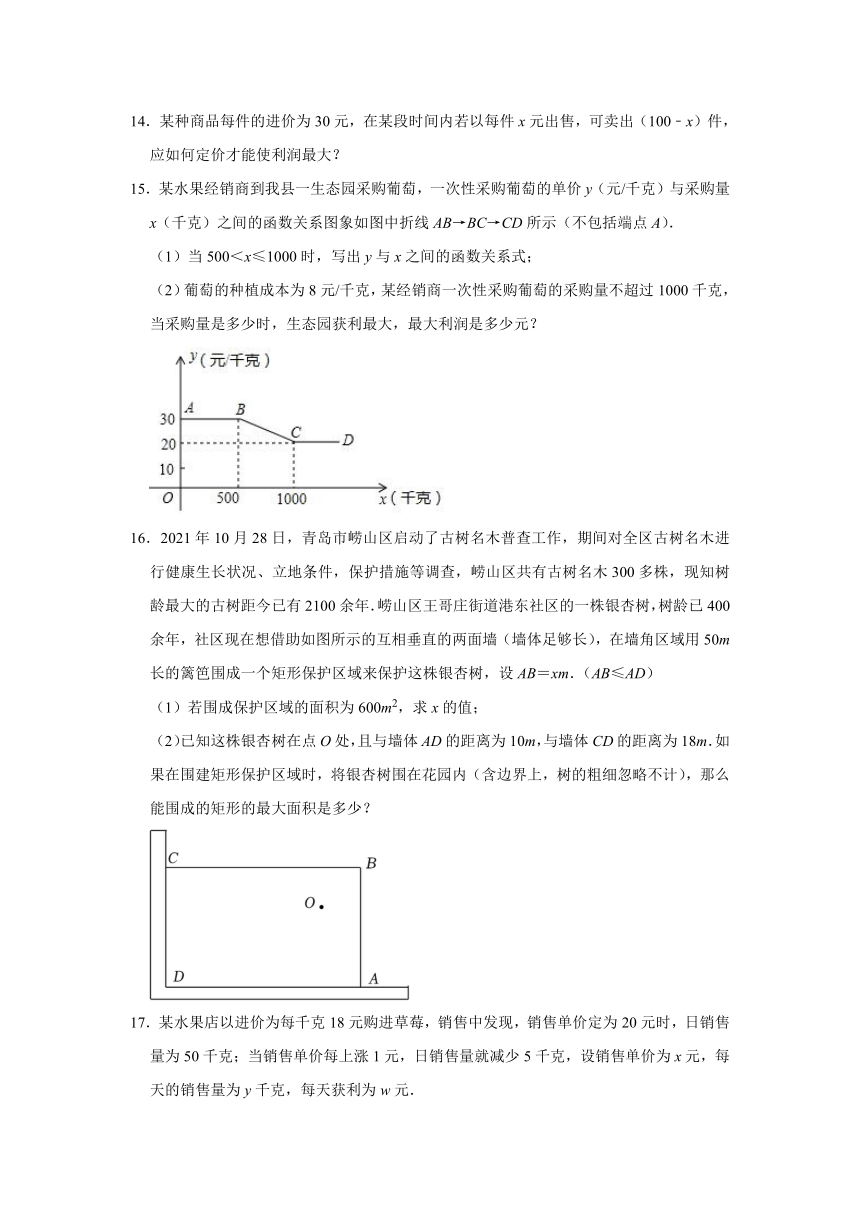
15.某水果经销商到我县一生态园采购葡萄,一次性采购葡萄的单价y(元/千克)与采购量x(千克)之间的函数关系图象如图中折线AB→BC→CD所示(不包括端点A).
(1)当500<x≤1000时,写出y与x之间的函数关系式;
(2)葡萄的种植成本为8元/千克,某经销商一次性采购葡萄的采购量不超过1000千克,当采购量是多少时,生态园获利最大,最大利润是多少元?
16.2021年10月28日,青岛市崂山区启动了古树名木普查工作,期间对全区古树名木进行健康生长状况、立地条件,保护措施等调查,崂山区共有古树名木300多株,现知树龄最大的古树距今已有2100余年.崂山区王哥庄街道港东社区的一株银杏树,树龄已400余年,社区现在想借助如图所示的互相垂直的两面墙(墙体足够长),在墙角区域用50m长的篱笆围成一个矩形保护区域来保护这株银杏树,设AB=xm.(AB≤AD)
(1)若围成保护区域的面积为600m2,求x的值;
(2)已知这株银杏树在点O处,且与墙体AD的距离为10m,与墙体CD的距离为18m.如果在围建矩形保护区域时,将银杏树围在花园内(含边界上,树的粗细忽略不计),那么能围成的矩形的最大面积是多少?
17.某水果店以进价为每千克18元购进草莓,销售中发现,销售单价定为20元时,日销售量为50千克;当销售单价每上涨1元,日销售量就减少5千克,设销售单价为x元,每天的销售量为y千克,每天获利为w元.
(1)求y与x之间的函数表达式;
(2)求w与x之间的函数表达式,并求该草莓售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果商家规定这种草莓每天的销售量不低于40千克,求每天销售利润的最大值是多少元?
18.新年前夕,金百超市在销售中发现:某服装平均每天可售出30套,每件盈利45元.为了迎接新年,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存.经市场调查发现:如果每套降价1元,那么平均每天就可多售出2套.
(1)要想平均每天在销售服装上盈利1750元,那么每套应降价多少元?
(2)商场要想每天获取最大利润,每套应降价多少元?
19.抗疫期间,全国人民众志成城,温州某商家决定将一个月的利润全部捐给当地医疗机构用于抗疫.该商家购进一批产品,成本10元/件,分为线上和线下两种销售方式.线下市场调查发现,当售价为12元时,月销量1200件,售价每增加1元,月销量减少100件.设月销量y(件),线下售价x(元).(12≤x≤24,且x为整数)
(1)求y关于x的函数关系式;
(2)若线上售价与线下相同,但每件产品商家需多付2元快递费,且线上月销量固定为500件.
①当售价x为多少时,线上和线下的月利润总和最大?并求出最大利润.
②商家第二个月决定继续捐款支持抗疫,捐款方式变为每卖出一件产品就捐款a元,为使商家线上和线下的月利润最低为700元,则a= .(直接写出答案)
参考答案
1.解:(1)由题意设销售数量y=kx+b(k≠0),
把(10,55),(26,39)代入函数解析式得:
,
解得:,
∴y=﹣x+65,
∴W=y(m﹣10)
=(﹣x+65)(x+20﹣10)
=﹣x2+55x+650(1≤x≤30,x为整数).
∴每天销售这种水果的利润W(元)与x(天)之间的函数关系式为W=﹣x2+55x+650(1≤x≤30,x为整数);
(2)当W=900时,则﹣x2+55x+650=900,
解得:x1=5,x2=50,
∵1≤x≤30,x为整数,
∴x=5,
答:当x=5时,日销售利润为900元;
(3)∵W=﹣x2+55x+650,
∴抛物线的对称轴为直线x=22.5,
∵a=﹣1<0,1≤x≤30,x为整数,
∴当x=22或x=23时,W取得最大值,
最大值为:﹣222+55×22+650=1376或﹣232+55×23+650=1376,
答:第22或23天销售这种水果的利润最大,最大日销售利润为1376元.
2.解:设每件涨价x元,每天获得利润为y元,根据题意得:
y=(32+x﹣24)(200﹣5x)
=﹣5x2+160x+1600
=﹣5(x﹣16)2+2880,
∵﹣5<0,
∴当x=16时,y取最大值,最大值是2880元,
答:每件涨价16元时,每天获得利润最大,,所获最大利润是2880元.
3.解:(1)根据题意得:y=(60+x﹣40)(300﹣10x)
=﹣10x2+100x+6000.
∴y与x之间的函数关系式为y=﹣10x2+100x+6000.
(2)令y=6250,则﹣10x2+100x+6000=6250,
解得x1=x2=5,
此时60+x=60+565(元),
∴当售价为65元时,当天的利润达到6250元.
4.解:(1)由题意可得,
y=(3﹣x)(50+×25)=﹣50x2+100x+150,
即y与x的函数表达式是y=﹣50x2+100x+150;
(2)由(1)知:y=﹣50x2+100x+150=﹣50(x﹣1)2+200,
∴当x=1时,y取得最大值,此时y=200,
答:若李大爷想让每天的利润最大化,应该降价1元销售,最大利润为200元.
5.解:(1)销售该床单每件的利润是(x﹣60)元,
故答案为:(x﹣60);
(2)由题意可设每月的销量w(件)与售价x(元)的函数解析式为w=kx+b,
把x=100,w=200和x=110,w=180代入解析式得:,
解得:,
∴月销量w=﹣2x+400件;
(3)由题意得,y=(x﹣60)(﹣2x+400),
即y=﹣2x2+520x﹣2400=﹣2(x﹣130)2+9800,
∵﹣2<0,
∴当x=130时,y有最大值,最大值为9800,
∴售价为130元时,当月的利润最大,最大利润是9800元.
6.解:(1)设该蔬菜销售单价y与销售月份x之间的关系式为y=kx+b,
将(3,5)和(6,3)代入得,
,
解得:,
∴y=﹣x+7,
当x=5时,y=﹣×5+7=≈3.7,
∴该蔬菜5月份的销售单价为3.7元;
(2)设成本与销售月份之间的关系式为:y=a(x﹣6)2+1,
把(3,4)代入得,4=a(3﹣6)2+1,
解得a=,
∴y=(x﹣6)2+1,即y=x2﹣4x+13,
当x=4时,y=≈2.3,
∴该蔬菜4月份每千克的成本为2.3元;
(3)设销售每千克蔬菜的收益为w元,
根据题意得:w=﹣x+7﹣(x2﹣4x+13)==﹣(x﹣5)2+,
∵﹣<0,
∴当x=5时,w有最大值,最大值为≈2.3,
∴5月份出售这种蔬菜,每千克的收益最大,每千克的最大收益是2.3元.
7.解:(1)由表中数据知,每件商品进价为:40﹣2400÷120=20(元),
∴每件进价 20元;
设一次函数解析式为y=kx+b,
根据题意,得,
解得:k=﹣2,b=100,
所以y与x的函数表达式为y=﹣2x+200;
故答案为:20,y=﹣2x+200;
(2)由题意,得w=(﹣2x+200)(x﹣20)=﹣2x2+240x﹣4000=﹣2(x﹣60)2+3200,
∵﹣2<0,
∴当x=60时,w有最大值,最大值为3200,
∴当每件售价为60元时,周销售利润w最大,最大利润为3200元;
(3)根据题意得,w=(x﹣20﹣4)(﹣2x+200)=﹣2x2+248x﹣4800=﹣2(x﹣62)2+2888,
∵﹣2<0,对称轴为x=62,24≤x≤m,
∴当50<m<62时,周销售最大利润为﹣2m2+248m﹣4800,
当m≥62时,周销售最大利润为2888元.
8.解:(1)当t=1时,m=40=40×12,
当t=2时,m=160=40×22,
当t=3时,m=360=40×32,
当t=4时,m=640=40×42,
∴m=40t2;
(2)将m=1000代入m=40t2,得1000=40t2,
解得t=5,
故5小时后所有人可以完成检测;
(3)检测t小时后检测处有w人,
由题意得:w=200×2++200t﹣40t2,
=﹣40(t﹣)2+150,
当t=时,w最大,最大为150,
故排队等候检测人数最多时有150人.
9.解:(1)设小张的“熟客“们这两年向小张采购鱼卷的年平均增长率为a,
则5000(1+a)2=7200,
整理得:(1+a)2=,
解得:x1=20%.x2=﹣(负根不合题意舍去),
答:小张的“熟客“们这两年向小张采购鱼卷的年平均增长率为20%;
(2)∵2020年底小张熟客们采订购鱼卷的数量占小张年底总销售量的,
∴2020年小张年总销量为:7200÷=9000 (箱),
设今年总利润为w元,价格下调x元,
则w=(15﹣x)(9000+1000x)=﹣1000x2+6000x+135000=﹣1000(x﹣3)2+144000,
∵a=﹣1000<0,1≤x≤5,
∴当x=3时,w有最大值,最大值为14400,
所以小张在今年年底能获得的最大利润是144000元.
10.解:(1)假设p与x成一次函数关系,设函数关系式为p=kx+b,
则,
解得:k=﹣30,b=1500,
∴p=﹣30x+1500,
检验:当x=35,p=450;当x=45,p=150;当x=50,p=0,符合一次函数解析式,
∴所求的函数关系为p=﹣30x+1500;
(2)设日销售利润w=p(x﹣30)=(﹣30x+1500)(x﹣30)
即w=﹣30x2+2400x﹣45000=﹣30(x﹣40)2+3000,
∵﹣30<0,
∴当x=40时,w有最大值,最大值为3000,
故这批农产品的销售价格定为40元,才能使日销售利润最大.
11.解:(1)设每件商品定价为x元,则每件商品的销售利润为(x﹣12)元,
根据题意得:(x﹣12)[240﹣10(x﹣20)]=2470,
整理得:x2﹣56x+775=0,
解得x1=25,x2=31,
∴该商品的定价应为22元或24元;
(2)由题意得:W=(m﹣12)[240﹣10(m﹣20)]=﹣10m2+560m﹣5280=﹣10(m﹣28)2+2560,
∵﹣10<0,
∴当m<28时,W随x的增大而增大,
∵每件商品销售单价不高于26元,
∴m≤26,
∴当m=26时,W最大,最大值为2520,
∴该商品的销售单价定为26元时,每天销售获得的利润最大,最大利润是2520元.
12.解:(1)∵正方形ABCD的边长为6cm,
∴AB=BC=6cm,
∴(6+6)÷3=4s,
∴点P的运动时间为4s,
故答案为:4;
(2)分三种情况:
当0<t≤2时,如图:
由题意得:
CP=3t,CQ=2t,
∴S=CP CQ
= 3t 2t
=3t2,
当2<t≤3时,如图:
由题意得:
CQ=2t,
∴S=CB CQ
=×6 2t
=6t,
当3<t≤4时,如图:
过点Q作QH⊥CD,垂足为H,过点Q作QE⊥AD,垂足为E,连接AQ,
由题意得:BP=3t﹣6,DQ=2t﹣6,AP=12﹣3t,
∵四边形ABCD是正方形,
∴∠ADB=∠CDB=45°,
∴QH=(2t﹣6)×=t﹣3,
QE=(2t﹣6)×=t﹣3,
∴QE=DE=t﹣3,
∴AE=AD﹣DE=6﹣t+3,
∴S=正方形ABCD的面积﹣△CQD的面积﹣△AQD的面积﹣△APQ的面积
=36﹣CD QH﹣AD QE﹣AP AE
=36﹣×6×(t﹣3)﹣×6×(t﹣3)﹣ (12﹣3t) (6﹣t+3)
=﹣t2+t+18,
综上所述:S=.
13.解:(1)由表中数据可知y与x满足一次函数,设y与x之间的函数关系式为y=kx+b,
根据题意,得:,
解得:,
∴y与x之间的函数关系式为y=﹣x+1000;
(2)w=(x﹣500)(﹣x+1000)=﹣x2+1500x﹣500000=﹣(x﹣750)2+62500,
∵﹣1<0,x≤700,
∴当x=700时,w取得最大值,最大值为60000,
∴w与x之间的函数关系式为w=﹣x2+1500x﹣500000,药材公司每周的最大利润为60000元;
(3)当w=40000时,﹣(x﹣750)2+62500=40000,
解得:x=900或x=600,
∵a=﹣1,
∴600≤x≤700,
∴销售单价x的取值范围为600≤x≤700.
14.解:设最大利润为w元,
则w=(x﹣30)(100﹣x)=﹣(x﹣65)2+1225,
∵﹣1<0,0<x<100,
∴当x=65时,二次函数有最大值1225,
∴定价是65元时,利润最大.
15.解:(1)设当500<x≤1000时,y与x之间的函数关系式为:y=ax+b,
∵BC段过点(500,30)和点(1000,20),
∴,
解得,,
∴当500<x≤1000时,y与x之间的函数关系式为:y=﹣0.02x+40;
(2)当采购量是x千克时,蔬菜种植基地获利W元,
当0<x≤500时,W=(30﹣8)x=22x,
∵22>0,
∴当x=500时,W有最大值11000元;
当500<x≤1000时,
W=(y﹣8)x=(﹣0.02x+32)x=﹣0.02x2+32x=﹣0.02(x﹣800)2+12800,
∵﹣0.02<0,
∴当x=800时,W有最大值为12800元,
综上所述,一次性采购量为800千克时,蔬菜种植基地能获得最大利润为12800元.
16.解:(1)∵AB=xm,则BC=(50﹣x)m,
∴x(50﹣x)=600,
解得:x1=20,x2=30,
答:x的值为20或30;
(2)∵AB=xm,BC=(50﹣x)m,
∴S=x(50﹣x)=﹣x2+50x=﹣(x﹣25)2+625,
∵在O处有一棵树与墙CD,AD的距离分别是18m和10m,
∵50﹣18=32,
∴10≤x≤32,
∴当x=25时,S取到最大值为625,
答:矩形面积S的最大值为625平方米.
17.解:(1)根据题意得,y=50﹣5(x﹣20)=﹣5x+150,
即y=﹣5x+150(x≥20);
(2)根据题意得,w=(x﹣18)(﹣5x+150)=﹣5x2+240x﹣2700,
即w与x之间的函数关系式为w=﹣5x2+240x﹣2700,
∵w=﹣5x2+240x﹣2700=﹣5(x﹣24)2+180,
且﹣5<0,
∴当x=24时,w有最大值,最大值为180,
答:w与x之间的函数关系式为:w=﹣5x2+240x﹣2700,该水果售价为每千克24元时,每天的销售利润最大,最大值为180元;
(3)由题意得,﹣5x+150≥40,
解得:x≤22,
∵w=﹣5(x﹣24)2+180,
∴当x≤24时,w随x的增大而增大,
∴当x=22时,w有最大值,最大值为:w=﹣5×(22﹣24)2+180=160,
答:商家每天销售利润的最大值是160元.
18.解:(1)设每套应降价m元,
由题意得(45﹣m)(30+2x)=1750,
解得m1=10,m2=20,
∵尽快减少库存,
∴m=20,
答:每套应降价20元;
(2)设每件衬衫应降价x元,总利润为w元,
根据题意得:w=(45﹣x)(30+2x)=﹣2(x﹣15)2+1800,
∴当x=15时,w取得最大值,此时w最大=1800,
答:商场要想每天获取最大利润,每套应降价15元,最大利润为1800元.
19.解:(1)根据题意得:y=1200﹣100(x﹣12)=﹣100x+2400,
∴y关于x的函数关系式为y=﹣100x+2400;
(2)①设线上和线下的月利润总和为w元,则
w=500(x﹣10﹣2)+y(x﹣10)
=500x﹣6000+(﹣100x+2400)(x﹣10)
=﹣100x2+3900x﹣30000,
=﹣100(x﹣)2+8025,
∵﹣100<0,12≤x≤24,且x为整数,
∴当x=19或20时,w有最大值,最大值为8000,
∴当x为19或20时,线上和线下的月利润总和达到最大,最大利润为8000元;
②设商家线上和线下的月利润总和为w元,
根据题意得,w=500(x﹣2﹣10﹣a)+(x﹣10﹣a)(﹣100x+2400),
即w=﹣100x2+(3900+100a)x﹣30000﹣2900a,
∵﹣100<0,抛物线开口向下,
∴x==,
当x=12,w取最小值为700时,700=﹣100×122+12×3900+12×100a﹣30000﹣2900a,
解得a=1,
此时抛物线对称轴为直线x==20,
20﹣12>24﹣20,满足题意.
当x=24,w取最小值为700时,700=﹣100×242+3900×24+24×100a﹣30000﹣2900a,
解得a=10.6,
此时抛物线对称轴为直线x==24.8,
24.8﹣24>24.8﹣12,不满足题意.
故答案为:1.
商品销售利润问题解答题专题训练(附答案)
1.某超市购进一批时令水果,成本为10元/千克,根据市场调研发现,这种水果在未来30天的销售单价m(元/千克)与时间x(天)之间的函数关系式为m=x+20(1≤x≤30,x为整数),且其日销售量y(千克)与时间x(天)之间的函数关系如图所示:
(1)求每天销售这种水果的利润W(元)与x(天)之间的函数关系式;
(2)求x为何值时,日销售利润为900元;
(3)直接写出哪一天销售这种水果的利润最大?最大日销售利润为多少元?
2.已知某商品的进价为每件24元,现在售价为每件32元,每天可售出200件.经市场调查发现:若该商品每件涨价1元,则每天就会少卖5件.
那么每件涨价多少元时每天获得利润最大?所获最大利润是多少元?
3.某商品的进价是每件40元,当售价每件60元时,当天可售出300件.进行不同程度的涨价后,发现每涨价1元,当天销售量减少10件.设商品售价每件涨价x元(x为正整数)时,当天售出商品的利润为y元.
(1)求y与x之间的函数关系式;
(2)如何定价,才能使商品当天的销售利润达到6250元?
4.李大爷每年春节期间都会购进一批新年红包销售,根据往年的销售经验,这种红包平均每天可销售50袋,每袋盈利3元,若每袋降价0.5元,平均每天可多售出25袋,设每袋降x元,平均每天的利润为y元.
(1)请求出y与x的函数表达式;
(2)若李大爷想让每天的利润最大化,应该降价多少元销售?最大利润为多少元?
5.已知某品牌床单进价为每件60元,每月的销量y(件)与售价x(元)的相关信息如表(符合一次函数关系):
售价(元/件) 100 110 120 130 …
月销售量(件) 200 180 160 140 …
(Ⅰ)销售该品牌床单每件的利润是 元(用含x的式子表示);
(Ⅱ)用含x的代数式表示月销量y;
(Ⅲ)设销售该品牌床单的月利润为w元,那么售价为多少时,当月的利润最大,最大利润是多少?
6.某种蔬菜在3﹣6月份的销售单价与销售月份之间的关系如图(甲)所示,成本与销售月份之间的关系如图(乙)所示.(图(甲)中4个点在一条直线上,图(乙)中的4个点在一条抛物线上)
(1)求该蔬菜5月份的销售单价.(精确到0.1元)
(2)求该蔬菜4月份每千克的成本.(精确到0.1元)
(3)哪个月出售这种蔬菜,每千克的收益最大?每千克的最大收益是多少元?(收益=售价﹣成本)
7.某商店销售一种商品,经市场调查发现:该商品的周销售量y(件)是售价x(元/件)的一次函数,其售价、周销售量、周销售利润w(元)的两组对应值如表:
售价x(元/件) 40 50
周销售量y(件) 120 100
周销售利润w(元) 2400 3000
注:周销售利润=周销售量×(售价﹣进价)
(1)每件商品的进价为 元/件,y与x的函数关系式为 (不要求写出自变量的取值范围);
(2)当每件商品售价x为多少元时,周销售利润w最大?并求出此时的最大利润;
(3)若该商品每件进价提高了4元,其每件售价不超过m元(m是大于50的常数,且是整数),该商店在销售中,周销售量与售价仍满足(1)中的函数关系,直接写出周销售的最大利润.
8.疫情期间,某核酸检测点要检测1000人,排队前来检测的人数y与时间x(小时)之间符合函数表达式:y=200x(x≤5)该检测点实际检测的人数m与时间t(小时)统计如下表所示:
t 0 1 2 3 4 …
m 0 40 160 360 640 …
(1)猜想该检测点检测的人数m关于t的函数表达式,并说明理由;
(2)几小时后所有人可以完成检测?
(3)因准备需要,排队2小时才开始检测,排队等候检测人数最多时有多少人?
9.鱼卷是泉州十大名小吃之一,不但本地人喜欢,还深受外来游客的赞赏.小张从事鱼卷生产和批发多年,有着不少来自零售商和酒店的客户,当地的习俗是农历正月没有生产鱼卷,客户正月所需要的鱼卷都会在农历十二月底进行一次性采购.2018年年底小张的“熟客”们共向小张采购了5000箱鱼卷,到2020年底“熟客”们采购了7200箱.
(1)求小张的“熟客“们这两年向小张采购鱼卷的年平均增长率;
(2)2020年底小张“熟客”们采订购鱼卷的数量占小张年底总销售量的,由于鱼卷受到游客们的青睐,小张做了一份市场调查,决定今年年底是否在网上出售鱼卷,若没有在网上出售鱼卷,则按去年的价格出售,每箱利润为15元,预计销售量与去年持平;若计划在网上出售鱼卷,则需把每箱售价下调1至5元,且每下调1元销售量可增加1000箱,求小张在今年年底能获得的最大利润是多少元?
10.农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格x(元/千克) 30 35 40 45 60
日销售量p(千克) 600 450 300 150 0
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式;
(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
11.某校数学综合实践小组去超市调查某种商品“十一”期间的销售情况,下面是调查后小明与其他两位同学交流的情况:
小明:据调查,该商品的进价为12元/件.
小亮:该商品定价为20元时,每天可售240件;
小颖:在定价为20元的基础上,每涨价1元,每天少售10件.
根据他们的对话,解决下列问题:
(1)若销售该商品每天能获利2470元,则该商品的定价应为多少元?
(2)设该商品的销售单价为m元时,每天销售该商品可获利W元,若每件商品销售单价不高于26元,则销售单价定为多少元时每天获利最大?最大利润是多少元?
12.如图,正方形ABCD的边长为6cm,P,Q两动点同时从点C出发,点P沿CB→BA以3cm/s的速度向终点A匀速运动,点Q沿CD→DB以2cm/s的速度向点B匀速运动,当点P到达终点A时,点Q同时停止运动.设点P的运动时间为t(s),△CPQ的面积为S(cm2).
(1)填空:点P的运动时间为 s;
(2)求S关于t的函数解析式,并直接写出自变量t的取值范围.
13.云南有着复杂的自然地理条件,十分有利于中药材的生长.某种中药材成本每斤500元某药材公司试销一段时间发现:每周的销售量y(斤)与销售单价x(元/斤)满足的关系如下表:
x(元/斤) 550 600 650 680
y(斤) 450 400 350 320
(1)请根据表中的数据写出y与x之间的函数关系式;
(2)根据有关部门规定,该药材售价不允许超过700元.该药材公司每周获利w元,试写w与x之间的函数关系式,并求出药材公司每周的最大利润.
(3)在(2)的条件下,若该药材公司每周获利不少于40000元,试确定销售单价x的取值范围.
14.某种商品每件的进价为30元,在某段时间内若以每件x元出售,可卖出(100﹣x)件,应如何定价才能使利润最大?
15.某水果经销商到我县一生态园采购葡萄,一次性采购葡萄的单价y(元/千克)与采购量x(千克)之间的函数关系图象如图中折线AB→BC→CD所示(不包括端点A).
(1)当500<x≤1000时,写出y与x之间的函数关系式;
(2)葡萄的种植成本为8元/千克,某经销商一次性采购葡萄的采购量不超过1000千克,当采购量是多少时,生态园获利最大,最大利润是多少元?
16.2021年10月28日,青岛市崂山区启动了古树名木普查工作,期间对全区古树名木进行健康生长状况、立地条件,保护措施等调查,崂山区共有古树名木300多株,现知树龄最大的古树距今已有2100余年.崂山区王哥庄街道港东社区的一株银杏树,树龄已400余年,社区现在想借助如图所示的互相垂直的两面墙(墙体足够长),在墙角区域用50m长的篱笆围成一个矩形保护区域来保护这株银杏树,设AB=xm.(AB≤AD)
(1)若围成保护区域的面积为600m2,求x的值;
(2)已知这株银杏树在点O处,且与墙体AD的距离为10m,与墙体CD的距离为18m.如果在围建矩形保护区域时,将银杏树围在花园内(含边界上,树的粗细忽略不计),那么能围成的矩形的最大面积是多少?
17.某水果店以进价为每千克18元购进草莓,销售中发现,销售单价定为20元时,日销售量为50千克;当销售单价每上涨1元,日销售量就减少5千克,设销售单价为x元,每天的销售量为y千克,每天获利为w元.
(1)求y与x之间的函数表达式;
(2)求w与x之间的函数表达式,并求该草莓售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果商家规定这种草莓每天的销售量不低于40千克,求每天销售利润的最大值是多少元?
18.新年前夕,金百超市在销售中发现:某服装平均每天可售出30套,每件盈利45元.为了迎接新年,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存.经市场调查发现:如果每套降价1元,那么平均每天就可多售出2套.
(1)要想平均每天在销售服装上盈利1750元,那么每套应降价多少元?
(2)商场要想每天获取最大利润,每套应降价多少元?
19.抗疫期间,全国人民众志成城,温州某商家决定将一个月的利润全部捐给当地医疗机构用于抗疫.该商家购进一批产品,成本10元/件,分为线上和线下两种销售方式.线下市场调查发现,当售价为12元时,月销量1200件,售价每增加1元,月销量减少100件.设月销量y(件),线下售价x(元).(12≤x≤24,且x为整数)
(1)求y关于x的函数关系式;
(2)若线上售价与线下相同,但每件产品商家需多付2元快递费,且线上月销量固定为500件.
①当售价x为多少时,线上和线下的月利润总和最大?并求出最大利润.
②商家第二个月决定继续捐款支持抗疫,捐款方式变为每卖出一件产品就捐款a元,为使商家线上和线下的月利润最低为700元,则a= .(直接写出答案)
参考答案
1.解:(1)由题意设销售数量y=kx+b(k≠0),
把(10,55),(26,39)代入函数解析式得:
,
解得:,
∴y=﹣x+65,
∴W=y(m﹣10)
=(﹣x+65)(x+20﹣10)
=﹣x2+55x+650(1≤x≤30,x为整数).
∴每天销售这种水果的利润W(元)与x(天)之间的函数关系式为W=﹣x2+55x+650(1≤x≤30,x为整数);
(2)当W=900时,则﹣x2+55x+650=900,
解得:x1=5,x2=50,
∵1≤x≤30,x为整数,
∴x=5,
答:当x=5时,日销售利润为900元;
(3)∵W=﹣x2+55x+650,
∴抛物线的对称轴为直线x=22.5,
∵a=﹣1<0,1≤x≤30,x为整数,
∴当x=22或x=23时,W取得最大值,
最大值为:﹣222+55×22+650=1376或﹣232+55×23+650=1376,
答:第22或23天销售这种水果的利润最大,最大日销售利润为1376元.
2.解:设每件涨价x元,每天获得利润为y元,根据题意得:
y=(32+x﹣24)(200﹣5x)
=﹣5x2+160x+1600
=﹣5(x﹣16)2+2880,
∵﹣5<0,
∴当x=16时,y取最大值,最大值是2880元,
答:每件涨价16元时,每天获得利润最大,,所获最大利润是2880元.
3.解:(1)根据题意得:y=(60+x﹣40)(300﹣10x)
=﹣10x2+100x+6000.
∴y与x之间的函数关系式为y=﹣10x2+100x+6000.
(2)令y=6250,则﹣10x2+100x+6000=6250,
解得x1=x2=5,
此时60+x=60+565(元),
∴当售价为65元时,当天的利润达到6250元.
4.解:(1)由题意可得,
y=(3﹣x)(50+×25)=﹣50x2+100x+150,
即y与x的函数表达式是y=﹣50x2+100x+150;
(2)由(1)知:y=﹣50x2+100x+150=﹣50(x﹣1)2+200,
∴当x=1时,y取得最大值,此时y=200,
答:若李大爷想让每天的利润最大化,应该降价1元销售,最大利润为200元.
5.解:(1)销售该床单每件的利润是(x﹣60)元,
故答案为:(x﹣60);
(2)由题意可设每月的销量w(件)与售价x(元)的函数解析式为w=kx+b,
把x=100,w=200和x=110,w=180代入解析式得:,
解得:,
∴月销量w=﹣2x+400件;
(3)由题意得,y=(x﹣60)(﹣2x+400),
即y=﹣2x2+520x﹣2400=﹣2(x﹣130)2+9800,
∵﹣2<0,
∴当x=130时,y有最大值,最大值为9800,
∴售价为130元时,当月的利润最大,最大利润是9800元.
6.解:(1)设该蔬菜销售单价y与销售月份x之间的关系式为y=kx+b,
将(3,5)和(6,3)代入得,
,
解得:,
∴y=﹣x+7,
当x=5时,y=﹣×5+7=≈3.7,
∴该蔬菜5月份的销售单价为3.7元;
(2)设成本与销售月份之间的关系式为:y=a(x﹣6)2+1,
把(3,4)代入得,4=a(3﹣6)2+1,
解得a=,
∴y=(x﹣6)2+1,即y=x2﹣4x+13,
当x=4时,y=≈2.3,
∴该蔬菜4月份每千克的成本为2.3元;
(3)设销售每千克蔬菜的收益为w元,
根据题意得:w=﹣x+7﹣(x2﹣4x+13)==﹣(x﹣5)2+,
∵﹣<0,
∴当x=5时,w有最大值,最大值为≈2.3,
∴5月份出售这种蔬菜,每千克的收益最大,每千克的最大收益是2.3元.
7.解:(1)由表中数据知,每件商品进价为:40﹣2400÷120=20(元),
∴每件进价 20元;
设一次函数解析式为y=kx+b,
根据题意,得,
解得:k=﹣2,b=100,
所以y与x的函数表达式为y=﹣2x+200;
故答案为:20,y=﹣2x+200;
(2)由题意,得w=(﹣2x+200)(x﹣20)=﹣2x2+240x﹣4000=﹣2(x﹣60)2+3200,
∵﹣2<0,
∴当x=60时,w有最大值,最大值为3200,
∴当每件售价为60元时,周销售利润w最大,最大利润为3200元;
(3)根据题意得,w=(x﹣20﹣4)(﹣2x+200)=﹣2x2+248x﹣4800=﹣2(x﹣62)2+2888,
∵﹣2<0,对称轴为x=62,24≤x≤m,
∴当50<m<62时,周销售最大利润为﹣2m2+248m﹣4800,
当m≥62时,周销售最大利润为2888元.
8.解:(1)当t=1时,m=40=40×12,
当t=2时,m=160=40×22,
当t=3时,m=360=40×32,
当t=4时,m=640=40×42,
∴m=40t2;
(2)将m=1000代入m=40t2,得1000=40t2,
解得t=5,
故5小时后所有人可以完成检测;
(3)检测t小时后检测处有w人,
由题意得:w=200×2++200t﹣40t2,
=﹣40(t﹣)2+150,
当t=时,w最大,最大为150,
故排队等候检测人数最多时有150人.
9.解:(1)设小张的“熟客“们这两年向小张采购鱼卷的年平均增长率为a,
则5000(1+a)2=7200,
整理得:(1+a)2=,
解得:x1=20%.x2=﹣(负根不合题意舍去),
答:小张的“熟客“们这两年向小张采购鱼卷的年平均增长率为20%;
(2)∵2020年底小张熟客们采订购鱼卷的数量占小张年底总销售量的,
∴2020年小张年总销量为:7200÷=9000 (箱),
设今年总利润为w元,价格下调x元,
则w=(15﹣x)(9000+1000x)=﹣1000x2+6000x+135000=﹣1000(x﹣3)2+144000,
∵a=﹣1000<0,1≤x≤5,
∴当x=3时,w有最大值,最大值为14400,
所以小张在今年年底能获得的最大利润是144000元.
10.解:(1)假设p与x成一次函数关系,设函数关系式为p=kx+b,
则,
解得:k=﹣30,b=1500,
∴p=﹣30x+1500,
检验:当x=35,p=450;当x=45,p=150;当x=50,p=0,符合一次函数解析式,
∴所求的函数关系为p=﹣30x+1500;
(2)设日销售利润w=p(x﹣30)=(﹣30x+1500)(x﹣30)
即w=﹣30x2+2400x﹣45000=﹣30(x﹣40)2+3000,
∵﹣30<0,
∴当x=40时,w有最大值,最大值为3000,
故这批农产品的销售价格定为40元,才能使日销售利润最大.
11.解:(1)设每件商品定价为x元,则每件商品的销售利润为(x﹣12)元,
根据题意得:(x﹣12)[240﹣10(x﹣20)]=2470,
整理得:x2﹣56x+775=0,
解得x1=25,x2=31,
∴该商品的定价应为22元或24元;
(2)由题意得:W=(m﹣12)[240﹣10(m﹣20)]=﹣10m2+560m﹣5280=﹣10(m﹣28)2+2560,
∵﹣10<0,
∴当m<28时,W随x的增大而增大,
∵每件商品销售单价不高于26元,
∴m≤26,
∴当m=26时,W最大,最大值为2520,
∴该商品的销售单价定为26元时,每天销售获得的利润最大,最大利润是2520元.
12.解:(1)∵正方形ABCD的边长为6cm,
∴AB=BC=6cm,
∴(6+6)÷3=4s,
∴点P的运动时间为4s,
故答案为:4;
(2)分三种情况:
当0<t≤2时,如图:
由题意得:
CP=3t,CQ=2t,
∴S=CP CQ
= 3t 2t
=3t2,
当2<t≤3时,如图:
由题意得:
CQ=2t,
∴S=CB CQ
=×6 2t
=6t,
当3<t≤4时,如图:
过点Q作QH⊥CD,垂足为H,过点Q作QE⊥AD,垂足为E,连接AQ,
由题意得:BP=3t﹣6,DQ=2t﹣6,AP=12﹣3t,
∵四边形ABCD是正方形,
∴∠ADB=∠CDB=45°,
∴QH=(2t﹣6)×=t﹣3,
QE=(2t﹣6)×=t﹣3,
∴QE=DE=t﹣3,
∴AE=AD﹣DE=6﹣t+3,
∴S=正方形ABCD的面积﹣△CQD的面积﹣△AQD的面积﹣△APQ的面积
=36﹣CD QH﹣AD QE﹣AP AE
=36﹣×6×(t﹣3)﹣×6×(t﹣3)﹣ (12﹣3t) (6﹣t+3)
=﹣t2+t+18,
综上所述:S=.
13.解:(1)由表中数据可知y与x满足一次函数,设y与x之间的函数关系式为y=kx+b,
根据题意,得:,
解得:,
∴y与x之间的函数关系式为y=﹣x+1000;
(2)w=(x﹣500)(﹣x+1000)=﹣x2+1500x﹣500000=﹣(x﹣750)2+62500,
∵﹣1<0,x≤700,
∴当x=700时,w取得最大值,最大值为60000,
∴w与x之间的函数关系式为w=﹣x2+1500x﹣500000,药材公司每周的最大利润为60000元;
(3)当w=40000时,﹣(x﹣750)2+62500=40000,
解得:x=900或x=600,
∵a=﹣1,
∴600≤x≤700,
∴销售单价x的取值范围为600≤x≤700.
14.解:设最大利润为w元,
则w=(x﹣30)(100﹣x)=﹣(x﹣65)2+1225,
∵﹣1<0,0<x<100,
∴当x=65时,二次函数有最大值1225,
∴定价是65元时,利润最大.
15.解:(1)设当500<x≤1000时,y与x之间的函数关系式为:y=ax+b,
∵BC段过点(500,30)和点(1000,20),
∴,
解得,,
∴当500<x≤1000时,y与x之间的函数关系式为:y=﹣0.02x+40;
(2)当采购量是x千克时,蔬菜种植基地获利W元,
当0<x≤500时,W=(30﹣8)x=22x,
∵22>0,
∴当x=500时,W有最大值11000元;
当500<x≤1000时,
W=(y﹣8)x=(﹣0.02x+32)x=﹣0.02x2+32x=﹣0.02(x﹣800)2+12800,
∵﹣0.02<0,
∴当x=800时,W有最大值为12800元,
综上所述,一次性采购量为800千克时,蔬菜种植基地能获得最大利润为12800元.
16.解:(1)∵AB=xm,则BC=(50﹣x)m,
∴x(50﹣x)=600,
解得:x1=20,x2=30,
答:x的值为20或30;
(2)∵AB=xm,BC=(50﹣x)m,
∴S=x(50﹣x)=﹣x2+50x=﹣(x﹣25)2+625,
∵在O处有一棵树与墙CD,AD的距离分别是18m和10m,
∵50﹣18=32,
∴10≤x≤32,
∴当x=25时,S取到最大值为625,
答:矩形面积S的最大值为625平方米.
17.解:(1)根据题意得,y=50﹣5(x﹣20)=﹣5x+150,
即y=﹣5x+150(x≥20);
(2)根据题意得,w=(x﹣18)(﹣5x+150)=﹣5x2+240x﹣2700,
即w与x之间的函数关系式为w=﹣5x2+240x﹣2700,
∵w=﹣5x2+240x﹣2700=﹣5(x﹣24)2+180,
且﹣5<0,
∴当x=24时,w有最大值,最大值为180,
答:w与x之间的函数关系式为:w=﹣5x2+240x﹣2700,该水果售价为每千克24元时,每天的销售利润最大,最大值为180元;
(3)由题意得,﹣5x+150≥40,
解得:x≤22,
∵w=﹣5(x﹣24)2+180,
∴当x≤24时,w随x的增大而增大,
∴当x=22时,w有最大值,最大值为:w=﹣5×(22﹣24)2+180=160,
答:商家每天销售利润的最大值是160元.
18.解:(1)设每套应降价m元,
由题意得(45﹣m)(30+2x)=1750,
解得m1=10,m2=20,
∵尽快减少库存,
∴m=20,
答:每套应降价20元;
(2)设每件衬衫应降价x元,总利润为w元,
根据题意得:w=(45﹣x)(30+2x)=﹣2(x﹣15)2+1800,
∴当x=15时,w取得最大值,此时w最大=1800,
答:商场要想每天获取最大利润,每套应降价15元,最大利润为1800元.
19.解:(1)根据题意得:y=1200﹣100(x﹣12)=﹣100x+2400,
∴y关于x的函数关系式为y=﹣100x+2400;
(2)①设线上和线下的月利润总和为w元,则
w=500(x﹣10﹣2)+y(x﹣10)
=500x﹣6000+(﹣100x+2400)(x﹣10)
=﹣100x2+3900x﹣30000,
=﹣100(x﹣)2+8025,
∵﹣100<0,12≤x≤24,且x为整数,
∴当x=19或20时,w有最大值,最大值为8000,
∴当x为19或20时,线上和线下的月利润总和达到最大,最大利润为8000元;
②设商家线上和线下的月利润总和为w元,
根据题意得,w=500(x﹣2﹣10﹣a)+(x﹣10﹣a)(﹣100x+2400),
即w=﹣100x2+(3900+100a)x﹣30000﹣2900a,
∵﹣100<0,抛物线开口向下,
∴x==,
当x=12,w取最小值为700时,700=﹣100×122+12×3900+12×100a﹣30000﹣2900a,
解得a=1,
此时抛物线对称轴为直线x==20,
20﹣12>24﹣20,满足题意.
当x=24,w取最小值为700时,700=﹣100×242+3900×24+24×100a﹣30000﹣2900a,
解得a=10.6,
此时抛物线对称轴为直线x==24.8,
24.8﹣24>24.8﹣12,不满足题意.
故答案为:1.
