人教版九年级数学上册第24章圆的有关性质选择专题训练(含解析)
文档属性
| 名称 | 人教版九年级数学上册第24章圆的有关性质选择专题训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 398.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 21:05:28 | ||
图片预览




文档简介
2022-2023学年人教版九年级数学上册《第24章圆的有关性质》选择专题训练(附答案)
1.如图,点A、B、D都在⊙O上,若∠ABD=40°,则∠AOD的度数为( )
A.40° B.80° C.100° D.140°
2.如图,已知OB,OD是⊙O的半径,BC、CD、DA是⊙O的弦,连接AB,若∠BOD=100°,则∠BCD度数为( )
A.100° B.120° C.130° D.140°
3.在圆内接四边形ABCD中,∠A、∠B、∠C的度数之比为2:4:7,则∠B的度数为( )
A.140° B.100° C.80° D.40°
4.如图,ABCD是⊙O的内接四边形,且∠ABC=125°,那么∠AOC等于( )
A.125° B.120° C.110° D.130°
5.如图,在⊙O中,点A、B、C在⊙O上,且∠ACB=108°,则∠α=( )
A.72° B.108° C.120° D.144°
6.在圆柱形油槽内装有一些油,截面如图所示,已知截面⊙O半径为5cm,油面宽AB为6cm,如果再注入一些油后,油面宽变为8cm,则油面AB上升了( )cm.
A.1 B.3 C.3或4 D.1或7
7.如图,AB是⊙O的直径,弦CD⊥AB于点E,若BE=5,AE=1,则弦CD的长是( )
A.5 B. C. D.6
8.小王不慎把一面圆形镜子打碎了,其中三块如图所示,三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是( )
A.① B.② C.③ D.都不能
9.如图,点A、B、C、D在⊙O上,OA⊥BC于点E,若BC=OB,则∠D的度数为( )
A.15° B.30° C.45° D.60°
10.如图,AB是⊙O的直径,CD是⊙O的弦.∠CAB=50°,则∠D=( )度.
A.30 B.40 C.50 D.60
11.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,若CD=6,BE=1,则AE=( )
A.5 B.8 C.9 D.10
12.如图,⊙O的半径为2,弦AB=2,则圆心O到弦AB的距离为( )
A.1 B. C. D.2
13.如图,以CD为直径的⊙O中,弦AB⊥CD于点M,若AB=24,CD=26.则MD的长为( )
A.5 B.7 C.8 D.10
14.如图,点A、B、C在⊙O上,∠ACB=54°,则∠AOB的度数是( )
A.90° B.100° C.108° D.110°
15.如图,AB是半圆O的直径,AB=4,点C,D在半圆上,OC⊥AB,D是(靠近C)弧CB的三等分点,点P是OC上的一个动点,则BP+DP的最小值为( )
A. B.2 C.3 D.2
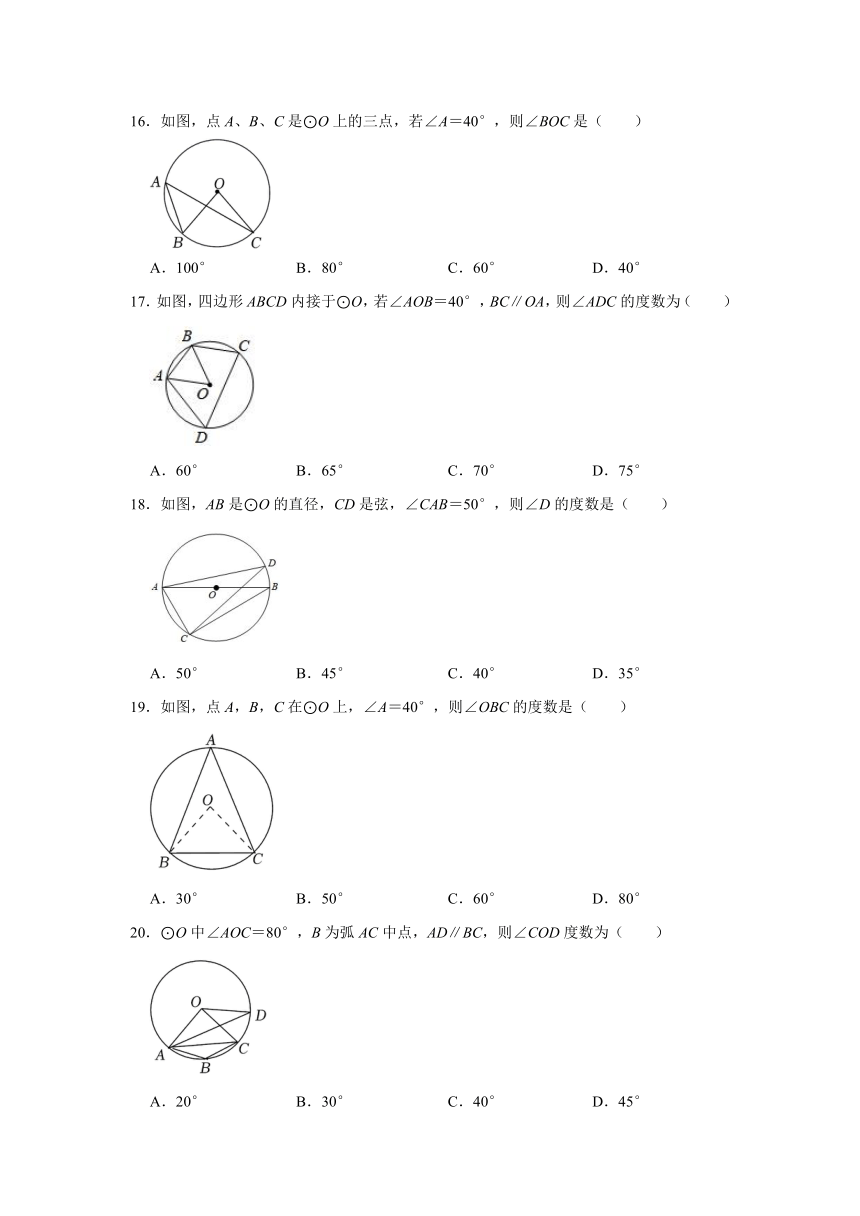
16.如图,点A、B、C是⊙O上的三点,若∠A=40°,则∠BOC是( )
A.100° B.80° C.60° D.40°
17.如图,四边形ABCD内接于⊙O,若∠AOB=40°,BC∥OA,则∠ADC的度数为( )
A.60° B.65° C.70° D.75°
18.如图,AB是⊙O的直径,CD是弦,∠CAB=50°,则∠D的度数是( )
A.50° B.45° C.40° D.35°
19.如图,点A,B,C在⊙O上,∠A=40°,则∠OBC的度数是( )
A.30° B.50° C.60° D.80°
20.⊙O中∠AOC=80°,B为弧AC中点,AD∥BC,则∠COD度数为( )
A.20° B.30° C.40° D.45°
参考答案
1.解:∵∠ABD=40°,
∴∠AOD=2∠ABD=2×40°=80°,
故选:B.
2.解:∵∠BOD和∠BAD都对,
∴∠BAD=∠BOD=×100°=50°,
∵∠BAD+∠BCD=180°,
∴∠BCD=180°﹣50°=130°.
故选:C.
3.解:设∠A的度数为2x,则∠B、∠C的度数分别为4x、7x,
由题意得:2x+7x=180°,
解得:x=20°,
则∠B=4x=80°,
故选:C.
4.解:∵四边形ABCD为圆内接四边形,
∴∠D+∠ABC=180°,
∴∠D=180°﹣125°=55°,
∴∠AOC=2∠D=110°.
故选:C.
5.解:作所对的圆周角∠ADB,如图,
∵∠ADB+∠ACB=180°,
∴∠ADB=180°﹣108°=72°,
∵∠ADB=∠AOB,
∴∠α=2×72°=144°.故选:D.
6.解:当油面没超过圆心O,油面宽CD为8cm时,
过O作OG⊥AB于G,交CD于H,连接OA,OC,
则OH⊥CD,
∴AG=AB=3(cm),CG=CD=4(cm),
∵截面⊙O半径为5cm,
∴OA=5cm,
∴OG===4(cm),OH===3(cm),
即弦AB的弦心距是4cm,弦CD的弦心距是3cm,
则OG﹣OH=4﹣3=1(cm),
即当油面没超过圆心O时,油上升了1cm;
当油面超过圆心O时,
同理得OH'=3cm,
则OG+OH'=4+3=7(cm),
即油面AB上升了7cm;
故选:D.
7.解:连接OC,
∵AB是⊙O的直径,弦CD⊥AB,BE=5,AE=1,
∴CD=2CE,∠OEC=90°,AB=AE+BE=6,
∴OC=OA=3,
∴OE=OA﹣AE=3﹣1=2,
在Rt△COE中,由勾股定理得:CE===,
∴CD=2CE=2,
故选:C.
8.解:第②块出现两条完整的弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.
故选:B.
9.解:∵OA⊥BC,
∴BE=EC=BC,=,
∵BC=OB,
∴=,
∴∠BOE=60°,
∴∠D=∠BOE=30°,
故选:B.
10.解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠CAB=50°,
∴∠B=90°﹣∠CAB=40°,
∴∠D=∠B=40°,
故选:B.
11.解:连接OC,设⊙O的半径为R,则AO=OB=OC=R,
∵AB⊥CD,AB过圆心O,CD=6,
∴CE=DE=3,∠CEO=90°,
由勾股定理得:OC2=CE2+OE2,
即R2=32+(R﹣1)2,
解得:R=5,
即OB=OA=5,
∵BE=1,
∴AE=AO+OB﹣BE=5+5﹣1=9,
故选:C.
12.解:过O作OC⊥AB于C,连接OA,
∵OC⊥AB,OC过圆心O,AB=2,
∴AC=BC=,∠OCA=90°,
由勾股定理得:OC===1,
即圆心O到弦AB的距离为1,
故选:A.
13.解:连接OA,如图所示:
∵CD是直径,AB是弦,AB⊥CD于M,AB=24,
∴AM=BM=AB=12,OA=OD=CD=13,
在Rt△OAM中,由勾股定理得:OM===5,
∴DM=OD﹣OM=13﹣5=8,
故选:C.
14.解:∵∠ACB和∠AOB都对,
∴∠AOB=2∠ACB=2×54°=108°.
故选:C.
15.解:如图,连接AD,PA,OD,DB.
∵OC⊥AB,OA=OB,
∴PA=PB,∠COB=90°,
∵=2,
∴∠DOB=×90°=60°,
∵OD=OB,
∴△OBD是等边三角形,
∴∠ABD=60°
∵AB是直径,
∴∠ADB=90°,
∴AD=AB sin∠ABD=2,
∵PB+PD=PA+PD≥AD,
∴PD+PB≥2,
∴PD+PB的最小值为2,
故选:B.
16.解:∵∠A和∠BOC都对,
∴∠BOC=2∠A=2×40°=80°.
故选:B.
17.解:∵BC∥OA,∠AOB=40°,
∴∠OBC=∠AOB=40°,
∵OA=OB,∠AOB=40°,
∴∠OBA=×(180°﹣40°)=70°,
∴∠ABC=∠OBA+∠OBC=40°+70°=110°,
∵四边形ABCD内接于⊙O,
∴∠ADC=180°﹣∠ABC=180°﹣110°=70°,
故选:C.
18.解:∵AB是直径,
∴∠ACB=90°,
∵∠CAB=50°,
∴∠ABC=90°﹣50°=40°,
∴∠D=∠ABC=40°,
故选:C.
19.解:∵∠A=40°,
∴∠BOC=2∠A=80°,
∵OB=OC,
∴∠OBC=∠OCB==50°.
故选:B.
20.解:∵AD∥BC,
∴∠DAC=∠BCA,
∴,
∵B为弧AC中点,
∴=,
∴∠COD=∠AOC=40°.
故选:C.
1.如图,点A、B、D都在⊙O上,若∠ABD=40°,则∠AOD的度数为( )
A.40° B.80° C.100° D.140°
2.如图,已知OB,OD是⊙O的半径,BC、CD、DA是⊙O的弦,连接AB,若∠BOD=100°,则∠BCD度数为( )
A.100° B.120° C.130° D.140°
3.在圆内接四边形ABCD中,∠A、∠B、∠C的度数之比为2:4:7,则∠B的度数为( )
A.140° B.100° C.80° D.40°
4.如图,ABCD是⊙O的内接四边形,且∠ABC=125°,那么∠AOC等于( )
A.125° B.120° C.110° D.130°
5.如图,在⊙O中,点A、B、C在⊙O上,且∠ACB=108°,则∠α=( )
A.72° B.108° C.120° D.144°
6.在圆柱形油槽内装有一些油,截面如图所示,已知截面⊙O半径为5cm,油面宽AB为6cm,如果再注入一些油后,油面宽变为8cm,则油面AB上升了( )cm.
A.1 B.3 C.3或4 D.1或7
7.如图,AB是⊙O的直径,弦CD⊥AB于点E,若BE=5,AE=1,则弦CD的长是( )
A.5 B. C. D.6
8.小王不慎把一面圆形镜子打碎了,其中三块如图所示,三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是( )
A.① B.② C.③ D.都不能
9.如图,点A、B、C、D在⊙O上,OA⊥BC于点E,若BC=OB,则∠D的度数为( )
A.15° B.30° C.45° D.60°
10.如图,AB是⊙O的直径,CD是⊙O的弦.∠CAB=50°,则∠D=( )度.
A.30 B.40 C.50 D.60
11.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,若CD=6,BE=1,则AE=( )
A.5 B.8 C.9 D.10
12.如图,⊙O的半径为2,弦AB=2,则圆心O到弦AB的距离为( )
A.1 B. C. D.2
13.如图,以CD为直径的⊙O中,弦AB⊥CD于点M,若AB=24,CD=26.则MD的长为( )
A.5 B.7 C.8 D.10
14.如图,点A、B、C在⊙O上,∠ACB=54°,则∠AOB的度数是( )
A.90° B.100° C.108° D.110°
15.如图,AB是半圆O的直径,AB=4,点C,D在半圆上,OC⊥AB,D是(靠近C)弧CB的三等分点,点P是OC上的一个动点,则BP+DP的最小值为( )
A. B.2 C.3 D.2
16.如图,点A、B、C是⊙O上的三点,若∠A=40°,则∠BOC是( )
A.100° B.80° C.60° D.40°
17.如图,四边形ABCD内接于⊙O,若∠AOB=40°,BC∥OA,则∠ADC的度数为( )
A.60° B.65° C.70° D.75°
18.如图,AB是⊙O的直径,CD是弦,∠CAB=50°,则∠D的度数是( )
A.50° B.45° C.40° D.35°
19.如图,点A,B,C在⊙O上,∠A=40°,则∠OBC的度数是( )
A.30° B.50° C.60° D.80°
20.⊙O中∠AOC=80°,B为弧AC中点,AD∥BC,则∠COD度数为( )
A.20° B.30° C.40° D.45°
参考答案
1.解:∵∠ABD=40°,
∴∠AOD=2∠ABD=2×40°=80°,
故选:B.
2.解:∵∠BOD和∠BAD都对,
∴∠BAD=∠BOD=×100°=50°,
∵∠BAD+∠BCD=180°,
∴∠BCD=180°﹣50°=130°.
故选:C.
3.解:设∠A的度数为2x,则∠B、∠C的度数分别为4x、7x,
由题意得:2x+7x=180°,
解得:x=20°,
则∠B=4x=80°,
故选:C.
4.解:∵四边形ABCD为圆内接四边形,
∴∠D+∠ABC=180°,
∴∠D=180°﹣125°=55°,
∴∠AOC=2∠D=110°.
故选:C.
5.解:作所对的圆周角∠ADB,如图,
∵∠ADB+∠ACB=180°,
∴∠ADB=180°﹣108°=72°,
∵∠ADB=∠AOB,
∴∠α=2×72°=144°.故选:D.
6.解:当油面没超过圆心O,油面宽CD为8cm时,
过O作OG⊥AB于G,交CD于H,连接OA,OC,
则OH⊥CD,
∴AG=AB=3(cm),CG=CD=4(cm),
∵截面⊙O半径为5cm,
∴OA=5cm,
∴OG===4(cm),OH===3(cm),
即弦AB的弦心距是4cm,弦CD的弦心距是3cm,
则OG﹣OH=4﹣3=1(cm),
即当油面没超过圆心O时,油上升了1cm;
当油面超过圆心O时,
同理得OH'=3cm,
则OG+OH'=4+3=7(cm),
即油面AB上升了7cm;
故选:D.
7.解:连接OC,
∵AB是⊙O的直径,弦CD⊥AB,BE=5,AE=1,
∴CD=2CE,∠OEC=90°,AB=AE+BE=6,
∴OC=OA=3,
∴OE=OA﹣AE=3﹣1=2,
在Rt△COE中,由勾股定理得:CE===,
∴CD=2CE=2,
故选:C.
8.解:第②块出现两条完整的弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.
故选:B.
9.解:∵OA⊥BC,
∴BE=EC=BC,=,
∵BC=OB,
∴=,
∴∠BOE=60°,
∴∠D=∠BOE=30°,
故选:B.
10.解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠CAB=50°,
∴∠B=90°﹣∠CAB=40°,
∴∠D=∠B=40°,
故选:B.
11.解:连接OC,设⊙O的半径为R,则AO=OB=OC=R,
∵AB⊥CD,AB过圆心O,CD=6,
∴CE=DE=3,∠CEO=90°,
由勾股定理得:OC2=CE2+OE2,
即R2=32+(R﹣1)2,
解得:R=5,
即OB=OA=5,
∵BE=1,
∴AE=AO+OB﹣BE=5+5﹣1=9,
故选:C.
12.解:过O作OC⊥AB于C,连接OA,
∵OC⊥AB,OC过圆心O,AB=2,
∴AC=BC=,∠OCA=90°,
由勾股定理得:OC===1,
即圆心O到弦AB的距离为1,
故选:A.
13.解:连接OA,如图所示:
∵CD是直径,AB是弦,AB⊥CD于M,AB=24,
∴AM=BM=AB=12,OA=OD=CD=13,
在Rt△OAM中,由勾股定理得:OM===5,
∴DM=OD﹣OM=13﹣5=8,
故选:C.
14.解:∵∠ACB和∠AOB都对,
∴∠AOB=2∠ACB=2×54°=108°.
故选:C.
15.解:如图,连接AD,PA,OD,DB.
∵OC⊥AB,OA=OB,
∴PA=PB,∠COB=90°,
∵=2,
∴∠DOB=×90°=60°,
∵OD=OB,
∴△OBD是等边三角形,
∴∠ABD=60°
∵AB是直径,
∴∠ADB=90°,
∴AD=AB sin∠ABD=2,
∵PB+PD=PA+PD≥AD,
∴PD+PB≥2,
∴PD+PB的最小值为2,
故选:B.
16.解:∵∠A和∠BOC都对,
∴∠BOC=2∠A=2×40°=80°.
故选:B.
17.解:∵BC∥OA,∠AOB=40°,
∴∠OBC=∠AOB=40°,
∵OA=OB,∠AOB=40°,
∴∠OBA=×(180°﹣40°)=70°,
∴∠ABC=∠OBA+∠OBC=40°+70°=110°,
∵四边形ABCD内接于⊙O,
∴∠ADC=180°﹣∠ABC=180°﹣110°=70°,
故选:C.
18.解:∵AB是直径,
∴∠ACB=90°,
∵∠CAB=50°,
∴∠ABC=90°﹣50°=40°,
∴∠D=∠ABC=40°,
故选:C.
19.解:∵∠A=40°,
∴∠BOC=2∠A=80°,
∵OB=OC,
∴∠OBC=∠OCB==50°.
故选:B.
20.解:∵AD∥BC,
∴∠DAC=∠BCA,
∴,
∵B为弧AC中点,
∴=,
∴∠COD=∠AOC=40°.
故选:C.
同课章节目录
