2022-2023学年高一上学期数学人教A版(2019)必修第一册2.1不等关系和不等式性质(第1课时)不等关系与不等式 课件-(共19张PPT)
文档属性
| 名称 | 2022-2023学年高一上学期数学人教A版(2019)必修第一册2.1不等关系和不等式性质(第1课时)不等关系与不等式 课件-(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 927.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 21:35:02 | ||
图片预览





文档简介
(共19张PPT)
第1课时
不等关系与不等式
第二章 一元二次函数、方程和不等式
人教A版必修第一册
2.1 等式性质与不等式性质
生活中有哪些不等关系的例子?
概念解析
不等关系与不等式
用数学符号“≠”、“>”、“<”、“≥”、“≤”连接两个数或代数式,以表示它们之间的不等关系,含有这些符号的式子,叫做__________.
不等式
大于 小于 大于或等于 小于或 等于 至多 至少 不小于 不大于
___ < ____ ≤ ____ ≥ _____ ≤
>
≥
≤
≥
不等式中自然语言与不等符号之间的转换:
新课讲解
问题1 你能用不等式或不等式组表示下列问题中的不等关系吗
(1)某路段限速40km/h;
(2)某品牌酸奶的质量检查规定,酸奶中脂肪的含量f应不少于2.5%,蛋白质的含量p应不少于2.3%;
设在该路段行驶的汽车的速度为v km/h,
“限速40km/h”就是速度的大小不能超过40,
于是0< v ≤ 40
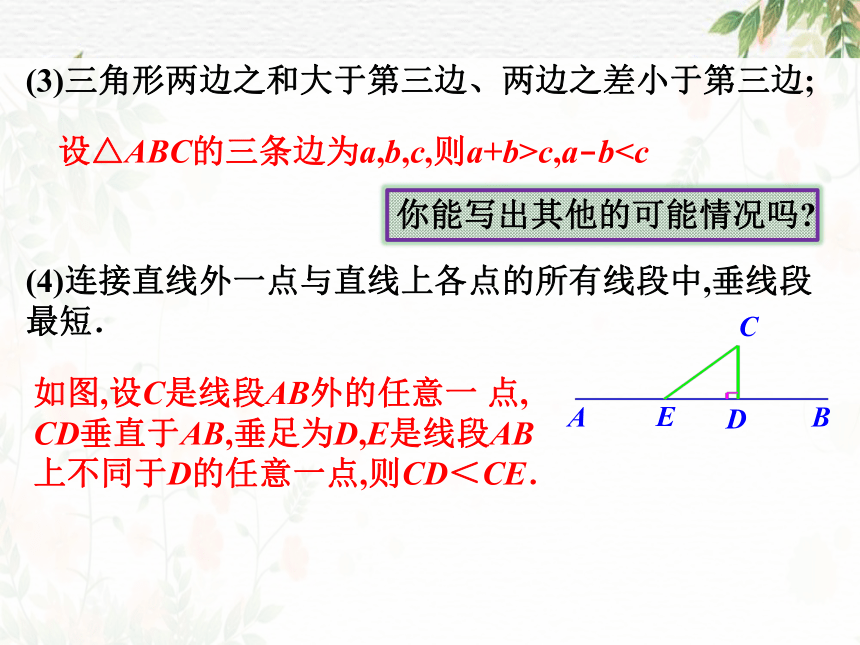
(3)三角形两边之和大于第三边、两边之差小于第三边;
(4)连接直线外一点与直线上各点的所有线段中,垂线段最短.
设△ABC的三条边为a,b,c,则a+b>c,a-b你能写出其他的可能情况吗
如图,设C是线段AB外的任意一 点,
CD垂直于AB,垂足为D,E是线段AB
上不同于D的任意一点,则CD<CE.
A
B
C
D
E
小结
用不等式表示实际问题中的不等关系:
从实际问题中抽象出不等关系
用字母表示不等关系中的量
用不等号连接字母,建立不等式
问题2 某种杂志原以每本2.5元的价格销售,可以售出8万本.据市场调查,若单价每提高0.1元销售量就可能相应减少2000本.如何定价才能使提价后的销售总收入不低于20万元
于是,不等关系“销售总收入不低于20万元”可以用
不等式表示为
设提价后每本杂志的定价为x元,则销售总收入为
求出不等式的解集,就能知道满足条件的杂志的定价范围
如何解这个不等式呢?
问题3 如何比较两个式子之间的大小关系?
由于数轴上的点与实数一一对应,所以可以利用数轴上点的位置关系来规定实数的大小关系.
如图 ,设a,b是两个实数,它们在数轴上所对应的点分别是A,B.那么,当点A在点B的左边时,ab.
x
A
B
a
b
aB
A
b
a
x
b如果a-b是正数,则a>b;如果a>b,则a-b为正数;
如果a-b是负数,则a如果a-b等于零,则a=b;如果a=b,则a-b等于零.
a>b a-b>0;
a=b a-b=0;
a这个基本事实可以表示为:
从上述基本事实可知,要比较两个实数的大小,可以转化为比较它们的差与0的大小.
基本事实:
比较两数(式)的大小的最基本和首选的方法:
解:
作差法
学以致用
例2 比较x2-x与x-2的大小.
解:(x2-x)-(x-2)=x2-2x+2
=(x-1)2+1,
因为(x-1)2≥0,
所以(x2-x)-(x-2)>0,
因此x2-x>x-2.
比较两个实数(或代数式)大小的步骤
(1)作差:对要比较大小的两个数(或式子)作差;
(2)变形:对差进行变形(因式分解、通分、配方、分子分母有理化等);
(3)定号:结合变形的结果及题设条件判断差的符号;
(4)结论:这种比较大小的方法通常称为作差比较法.
归纳总结
练习2 比较x2-x与x-2的大小.
解:(x2-x)-(x-2)=x2-2x+2
=(x-1)2+1,
因为(x-1)2≥0,
所以(x2-x)-(x-2)>0,
因此x2-x>x-2.
A
B
C
D
E(FGH)
a
b
A
D
C
B
H
F
G
E
适用范围:
a,b∈R
思考:当a=b时会出现什么情况?
正方形EFGH 缩为一个点,这时有a +b =2ab
一般地, a,b∈R,有
a +b ≥2ab,
当且仅当a=b时,等号成立.
思考
能否利用作差法比较 a +b 与2ab的大小
证明: a +b -2ab=(a-b)
因为a,b∈R,(a-b) ≥0,
当且仅当a=b时,等号成立,
所以 a +b ≥2ab,
当且仅当a=b时,等号成立
1.完成一项装修工程,请木工需付工资每人500元,请瓦工需付工资每人400元,现有工人工资预算20 000元,设木工x(x≥0)人,瓦工y(y≥0)人,则关于工资x,y满足的不等关系是( )
A.5x+4y<200 B.5x+4y≥200
C.5x+4y=200 D.5x+4y≤200
达标训练
D
2.设M=x2,N=-x-1,则M与N的大小关系是( )
A.M>N B.M=N
C.MA
祝你学习进步
感谢观看
第1课时
不等关系与不等式
第二章 一元二次函数、方程和不等式
人教A版必修第一册
2.1 等式性质与不等式性质
生活中有哪些不等关系的例子?
概念解析
不等关系与不等式
用数学符号“≠”、“>”、“<”、“≥”、“≤”连接两个数或代数式,以表示它们之间的不等关系,含有这些符号的式子,叫做__________.
不等式
大于 小于 大于或等于 小于或 等于 至多 至少 不小于 不大于
___ < ____ ≤ ____ ≥ _____ ≤
>
≥
≤
≥
不等式中自然语言与不等符号之间的转换:
新课讲解
问题1 你能用不等式或不等式组表示下列问题中的不等关系吗
(1)某路段限速40km/h;
(2)某品牌酸奶的质量检查规定,酸奶中脂肪的含量f应不少于2.5%,蛋白质的含量p应不少于2.3%;
设在该路段行驶的汽车的速度为v km/h,
“限速40km/h”就是速度的大小不能超过40,
于是0< v ≤ 40
(3)三角形两边之和大于第三边、两边之差小于第三边;
(4)连接直线外一点与直线上各点的所有线段中,垂线段最短.
设△ABC的三条边为a,b,c,则a+b>c,a-b
如图,设C是线段AB外的任意一 点,
CD垂直于AB,垂足为D,E是线段AB
上不同于D的任意一点,则CD<CE.
A
B
C
D
E
小结
用不等式表示实际问题中的不等关系:
从实际问题中抽象出不等关系
用字母表示不等关系中的量
用不等号连接字母,建立不等式
问题2 某种杂志原以每本2.5元的价格销售,可以售出8万本.据市场调查,若单价每提高0.1元销售量就可能相应减少2000本.如何定价才能使提价后的销售总收入不低于20万元
于是,不等关系“销售总收入不低于20万元”可以用
不等式表示为
设提价后每本杂志的定价为x元,则销售总收入为
求出不等式的解集,就能知道满足条件的杂志的定价范围
如何解这个不等式呢?
问题3 如何比较两个式子之间的大小关系?
由于数轴上的点与实数一一对应,所以可以利用数轴上点的位置关系来规定实数的大小关系.
如图 ,设a,b是两个实数,它们在数轴上所对应的点分别是A,B.那么,当点A在点B的左边时,a
x
A
B
a
b
a
A
b
a
x
b
如果a-b是负数,则a
a>b a-b>0;
a=b a-b=0;
a这个基本事实可以表示为:
从上述基本事实可知,要比较两个实数的大小,可以转化为比较它们的差与0的大小.
基本事实:
比较两数(式)的大小的最基本和首选的方法:
解:
作差法
学以致用
例2 比较x2-x与x-2的大小.
解:(x2-x)-(x-2)=x2-2x+2
=(x-1)2+1,
因为(x-1)2≥0,
所以(x2-x)-(x-2)>0,
因此x2-x>x-2.
比较两个实数(或代数式)大小的步骤
(1)作差:对要比较大小的两个数(或式子)作差;
(2)变形:对差进行变形(因式分解、通分、配方、分子分母有理化等);
(3)定号:结合变形的结果及题设条件判断差的符号;
(4)结论:这种比较大小的方法通常称为作差比较法.
归纳总结
练习2 比较x2-x与x-2的大小.
解:(x2-x)-(x-2)=x2-2x+2
=(x-1)2+1,
因为(x-1)2≥0,
所以(x2-x)-(x-2)>0,
因此x2-x>x-2.
A
B
C
D
E(FGH)
a
b
A
D
C
B
H
F
G
E
适用范围:
a,b∈R
思考:当a=b时会出现什么情况?
正方形EFGH 缩为一个点,这时有a +b =2ab
一般地, a,b∈R,有
a +b ≥2ab,
当且仅当a=b时,等号成立.
思考
能否利用作差法比较 a +b 与2ab的大小
证明: a +b -2ab=(a-b)
因为a,b∈R,(a-b) ≥0,
当且仅当a=b时,等号成立,
所以 a +b ≥2ab,
当且仅当a=b时,等号成立
1.完成一项装修工程,请木工需付工资每人500元,请瓦工需付工资每人400元,现有工人工资预算20 000元,设木工x(x≥0)人,瓦工y(y≥0)人,则关于工资x,y满足的不等关系是( )
A.5x+4y<200 B.5x+4y≥200
C.5x+4y=200 D.5x+4y≤200
达标训练
D
2.设M=x2,N=-x-1,则M与N的大小关系是( )
A.M>N B.M=N
C.M
祝你学习进步
感谢观看
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
